Nevezetes sorozatok

Nevezetes sorozatok

A következő programokat nem Turbo Pascalban, hanem Free Pascalban írtam meg, mivel ebben a nyelvben található meg az Int64 típus, és így elég sok lépésig lehetett futtatni az iterációkat.

A Fibonacci sorozat

A Fibonacci sorozat elemei a következők:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Képzési szabálya pedig ez: az első és második eleme legyen 1, majd a harmadiktól kezdve minden elem az előző két elemnek az összege. Képletben:

a_n = a_n-1+a_n-2

Írjunk programot, amely Fibonacci sorozat elemeit állítja elő. Egészítsük ki azzal, hogy minden lépésben az egymást követő elemek hányadosát is határozzuk meg. Lehessen megadni, hogy hány elemet határozzon meg a program. Ellenőrzött adatbevitel mellett adjunk korlátot az elemek számára. A programot Free Pascal-ban írtam meg. A alkalmazott legbővebb adattipúsok mellett a maximális meghatározható elemszám 91. Ezt is vegyük figyelembe a kódolásnál. A program listája:

Program Fibonacc;
Uses Crt;
Var A, B, C: Int64;
    I, N: Word;
    Sz: String;
    Kod: Integer;
Begin
  TextMode(CO80);
  ClrScr;
  Write('Iterációk száma (kisebb mint 91): ');
  ReadLn(Sz); Val(Sz,N,Kod);
  If Kod>0 Then N:= 90; If N>90 Then N:= 90;
  A:= 1; B:= 1;
  For I:= 1 To N Do
  Begin
    WriteLn(I:3,'/',N:3,': ',A:22, B:22, B/A:25:20);
    C:= A+B; A:= B; B:= C;
  End;
  Repeat Until Keypressed;
End.

Futtassuk a programot a maximális megengedett értékig. Az utolsó elemeket láthatjuk a következő képernyőn:

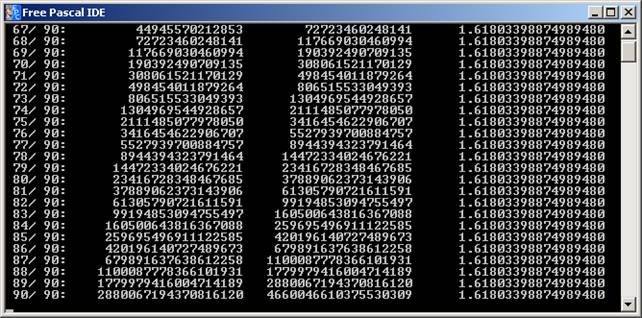
Futtassuk a programot a 23. lépésig:

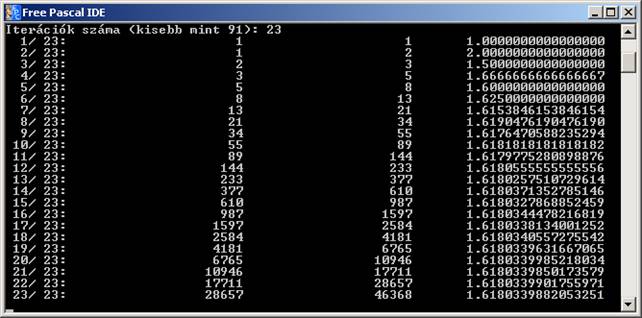
Látható, hogy a hányados 1,618 környékén kezd egyre kisebb értékkel változni. Keressük meg, hogy hanyadik elemtől lesz ez változatlan (16 tizedes érték pontossággal). Ezt a 43. lépéstől láthatjuk:

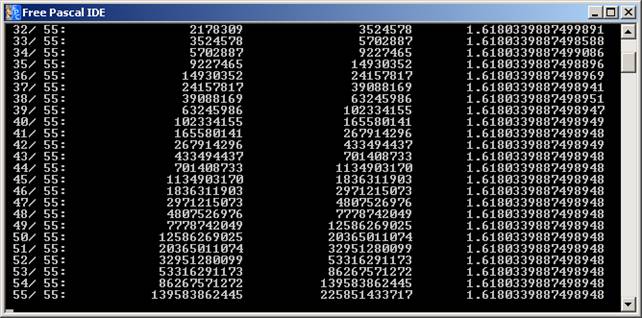
A Leibniz-féle sor a Pi közelítésére

Közismert érték a kör átmérőjének és kerületének aránya, melyet szokás Ludolph féle számnak is nevezni, amit röviden Pi-nek nevezünk és 3,14-nek ismerjük legjobban. Ez a szám irracionális (nem szakaszos végtelen tizedes tört), sőt transzcendens, ami azt jelenti, hogy nincs olyan algebrai egyenlet, melynek megoldása lenne. Másképpen nincs rá olyan képlet, amely a csak négy alapművelet és a gyökvonás segítségével véges lépésben a Pi-t előállítaná. Praktikusan nem ismert minden számjegye, csak elég sok, manapság már billiárd nagyságrendű számjegyét meghatározták.

A számjegyek megismerése számítógéppel gép és idő függvénye. Számos előállító képletéből én az egyik legegyszeűbbet, a Leibniz-féle sort választottam. Ez pedig a következő:

pi/4 = 1/1 – 1/3 + 1/5 – 1/7 + 1/9 – ...

A képzési szabály igen egyszerű, a páratlan számok reciprokainak váltott előjeles összevonásával a Pi negyedét kapjuk. A program listája:

Program PiKozel;
Uses Crt;
Var I, N: Word;
    PK: Real;
    Kod, EJ: Integer;
    Sz: String;
Begin
  TextMode(CO80);
  ClrScr;
  Write('Iterációk száma (kisebb mint 20001): ');
  ReadLn(Sz); Val(Sz,N,Kod);
  If Kod>0 Then N:= 1000; If N>20000 Then N:= 20000;
  PK:= 1;
  For I:= 1 To N Do
  Begin
    If Odd(I) Then EJ:= -1 Else EJ:= 1;
    PK:= PK+EJ/(2*I+1);
    WriteLn(I:5,'/',N:5,':',4*PK:20:14);
  End;
  TextColor(Yellow);
  WriteLn('Pi:         ',Pi:20:14);
  Repeat Until Keypressed;
End.

Például 20000 lépés alatt a következő eredményre jutunk:

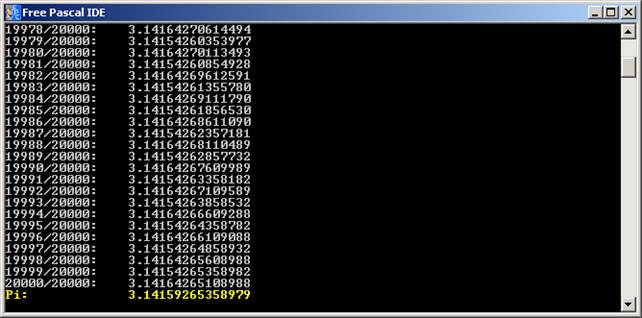
A képernyő utolsó sorában a gép által ismert Pi látható 14 tizedes jegy pontossággal.

A természetes alapú logaritmus alapjának közelítése

Mint ismeretes a természetes alapú logaritmus alapszáma egy 2,71 körüli érték, melyet e betűvel jelölünk. Ez a szám is transzcendens, akárcsak a Pi. Közelítő meghatározásának alapja a következő sorozat, melynek a határértéke e, n tart végtelen esetén:

a_n = (1+1/n)ⁿ

A sorozat határértékének közelítését a minél magasabb hatvány meghatározása jelenti. A listában ez a határszám az 1 millió, de nagyobb is beírható. A program listája:

Program LogNat;
Uses Crt;
Var I, N: LongInt;
    Sz: String;
    Kod: Integer;
Function Hatv(N: LongInt): Real;
Var I: LongInt;
    P: Real;
Begin
  P:= 1;
  For I:= 1 To N Do P:= (1+1/N)*P;
  Hatv:= P;
End;
Begin
  TextMode(CO80);
  ClrScr;
  Write('Iterációk száma (kisebb mint 1000000): ');
  ReadLn(Sz); Val(Sz,N,Kod);
  If Kod>0 Then N:= 1000; If N>999999 Then N:= 20000;
  For I:= 1 To N Do
  WriteLn(I:6,'/',N:6,':',Hatv(I):18:14);
  TextColor(Red+8);
  WriteLn('999999:       ',Hatv(999999):18:14);
  TextColor(Yellow);
  WriteLn('e:            ',Exp(1):18:14);
  Repeat Until Keypressed;
End.

A sorozat szigorúan monoton növekedő, ha 1000 lépést végzünk el, akkor az érték 2 tizedesre pontos, ha egymilliót, akkor 5-re. A képernyő utolsó előtti sorában pirossal a 999999. lépés, az utolsóban a gép által ismert e érték látható 14 titedes jegyre.