Lineáris algebra demonstrációs program

Ez a program azt próbálja bemutatni, hogy a kétdimenziós vektortérben hogyan hatnak az egyes vektorokra a lineáris transzformációk. Megadhatjuk a transzformáció mátrixát, megadhatjuk a koordinátarendszerben az egységet. A statikus képen az egységkör kerületére mutató vektorok képét fehér színnel rajzolja a program (a vektor végét jelző nyíltól eltekintve), majd sárgával a transzformált vektorokat, melyek mindig egy ellipszis (speciális esetben egy kör) kerületére mutatnak. Animációt is bekapcsolhatunk, ekkor az eredeti vektor piros, a képvektor kék színben jelenik meg, és a változási sebesség menet közben módosítható. Jó szórakozást a program használatához.

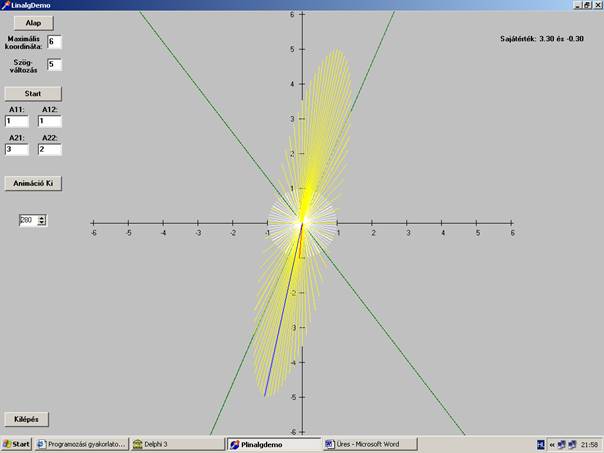
A program egy futási képe:

A program listája:

unit ULinalgDemo;

interface

uses
  Windows, Messages, SysUtils, Classes,

Graphics, Controls, Forms, Dialogs, StdCtrls, ExtCtrls, Spin;

type
  TfmLinalgDemo = class(TForm)
    btKilepes: TButton;
    btStart: TButton;
    lbA11: TLabel;
    edA11: TEdit;
    lbA12: TLabel;
    edA12: TEdit;
    lbA21: TLabel;
    edA21: TEdit;
    lbA22: TLabel;
    edA22: TEdit;
    btAlap: TButton;
    edMaxKoord: TEdit;
    lbMaxKoord: TLabel;
    lbSajat: TLabel;
    lbSzogValt: TLabel;
    edSzogValt: TEdit;
    btAnimacio: TButton;
    tiIdozito: TTimer;
    seSebes: TSpinEdit;
    lbSebes: TLabel;
Procedure KepTorles;
Procedure Alap;
procedure btAlapClick(Sender: TObject);
Procedure MatrixOlvas;
Procedure TranszformKepre;
Procedure SajatErtek;
Procedure IrEgyenes(M, B: Real);
Procedure NormEgyenes(A, B, C: Real);
procedure btStartClick(Sender: TObject);
procedure btKilepesClick(Sender: TObject);
procedure tiIdozitoTimer(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure btAnimacioClick(Sender: TObject);
procedure seSebesChange(Sender: TObject);
procedure edA11Change(Sender: TObject);
procedure edA12Change(Sender: TObject);
procedure edA21Change(Sender: TObject);
procedure edA22Change(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

Const Max=5000;

var
  fmLinalgDemo: TfmLinalgDemo;
  Xm,Ym, Xk,Yk: Integer;            //képenyő és félképernyő méretek
  N: Integer;                       //vektorok száma az egységkörben
  P: Integer;                       //maximális egész koordináta
  D: Integer;                       //egész koordináta-távolsága pixelben
  Ds: Integer;                      //fokonkénti rajzolás
A: Array[1..2,1..2] Of Real;      //a lineáris transzformáció mátrixa
  K1, K2: Real;                     //a lineáris transzformáció sajátértékei
  Animal: Boolean;                  //az animációt figyelő
  AN: Integer;                      //az animációban aktuális vektor sorszáma

implementation

{$R *.DFM}

Procedure TfmLinalgDemo.KepTorles;  //a képernyő törlése
Var R: TRect;
Begin
  R.Left:= 0; R.Top:= 0; R.Right:= Xm; R.Bottom:= Ym; Canvas.FillRect(R);
  lbMaxKoord.Repaint; lbSzogValt.Repaint;
  lbA11.Repaint; lbA12.Repaint;
  lbA21.Repaint; lbA22.Repaint;
  lbSajat.Repaint;
End;

procedure TfmLinalgDemo.Alap;       //koordinátarendszer és az egységkör
Var I: Integer;
Begin
  Xm:= ClientWidth; Ym:= ClientHeight;
  Xk:= Xm Div 2; Yk:= Ym Div 2; D:= Yk Div P;
With Canvas Do
Begin
    Pen.Color:= clBlack;
    MoveTo(Xk,0); LineTo(Xk,Ym);
    MoveTo(Xk-Yk,Yk); LineTo(Xk+Yk,Yk);
For I:= 1 To P Do
Begin
      MoveTo(Xk+I*D,Yk-5); LineTo(Xk+I*D,Yk+5);
      TextOut(Xk+I*D,Yk+10,IntToStr(I));
      MoveTo(Xk-I*D,Yk-5); LineTo(Xk-I*D,Yk+5);
      TextOut(Xk-I*D-4,Yk+10,'-'+IntToStr(I));
      MoveTo(Xk-5,Yk+I*D); LineTo(Xk+5,Yk+I*D);
TextOut(Xk-20,Yk+I*D-6,'-'+IntToStr(I));
      MoveTo(Xk-5,Yk-I*D); LineTo(Xk+5,Yk-I*D);
      TextOut(Xk-20,Yk-I*D-6,IntToStr(I));
End;
    Pen.Color:= clWhite;
For I:= 1 To N Do
Begin
      MoveTo(Xk,Yk);
      LineTo(Xk + Round(D*Cos(I*Ds*Pi/180)), Yk - Round(D*Sin(I*Ds*Pi/180)));
End;
End;
End;

procedure TfmLinalgDemo.btAlapClick(Sender: TObject);
Var Kod: Integer;
begin
  Val(edSzogValt.Text,Ds,Kod); N:= Round(360/Ds);
  Val(edMaxKoord.Text,P,Kod);
  KepTorles; Alap;
  Animal:= False; btAnimacio.Enabled:= False;
end;

Procedure TfmLinalgDemo.MatrixOlvas; //a maátrix beolvasása ellenőrzés nélkül
Var Kod: Integer;
Begin
  Val(edA11.Text,A[1,1],Kod); Val(edA12.Text,A[1,2],Kod);
  Val(edA21.Text,A[2,1],Kod); Val(edA22.Text,A[2,2],Kod);
End;

procedure TfmLinalgDemo.edA11Change(Sender: TObject);
begin
  MatrixOlvas; Keptorles;
  btAlapClick(Sender); btStartClick(Sender);
end;

procedure TfmLinalgDemo.edA12Change(Sender: TObject);
begin
  MatrixOlvas; Keptorles;
  btAlapClick(Sender); btStartClick(Sender);
end;

procedure TfmLinalgDemo.edA21Change(Sender: TObject);
begin
  MatrixOlvas; Keptorles;
btAlapClick(Sender); btStartClick(Sender);
end;

procedure TfmLinalgDemo.edA22Change(Sender: TObject);
begin
  MatrixOlvas; Keptorles;
  btAlapClick(Sender); btStartClick(Sender);
end;

Procedure TfmLinalgDemo.TranszformKepre; //a kör transzformáltjának rajzolása
Var I: Word;
Begin
With Canvas Do
Begin
    Pen.Color:= clYellow;
For I:= 1 To N Do
Begin
      MoveTo(Xk,Yk);
      LineTo(Xk + Round(A[1,1]*D*Cos(I*Ds*Pi/180)+A[1,2]*D*Sin(I*Ds*Pi/180)),
             Yk - Round(A[2,1]*D*Sin(I*Ds*Pi/180)+A[2,2]*D*Sin(I*Ds*Pi/180)));
End;
End;
End;

Procedure TfmLinalgDemo.SajatErtek;      //a sájátértékek meghatározása
Var DetA, SpurA, Di: Real;
    S1, S2, S: String;
    N1, N2, M1, M2: Real;
Begin
  DetA:= A[1,1]*A[2,2]-A[2,1]*A[1,2];    //a mátrix determinánsa
  SpurA:= A[1,1]+A[2,2];                 //a mátrix spurja
//a karakterisztikus egyenlet: k*k - SpurA*k + DetA = 0
  Di:= SpurA*SpurA-4*DetA;               //a karakterisztikus egyenlet
//diszkriminánsa
If Di>=0 Then //két valós gyök
Begin
    K1:= (SpurA+Sqrt(Di))/2;              //sajátértékek
K2:= (SpurA-Sqrt(Di))/2;
    Str(K1:4:2, S1);
    Str(K2:4:2, S2);
    S:= 'Sajátérték: '+S1+' és '+S2;
    N1:= A[2,2]-A[1,2]-K1;
    N2:= A[2,2]-A[1,2]-K2;
With Canvas Do
Begin
If N1<>0 Then M1:= (A[1,1]-A[2,1]-K1)/N1 Else M1:= Max;
If N2<>0 Then M2:= (A[1,1]-A[2,1]-K2)/N2 Else M2:= Max;
      Pen.Color:= clGreen;
If M1=0 Then M1:= 1/Max; IrEgyenes(M1,0);
If M2=0 Then M2:= 1/Max; IrEgyenes(M2,0);
End;
End
Else S:= 'Nincs sajátérték';
  lbSajat.Caption:= S;
End;

Procedure TfmLinalgDemo.IrEgyenes(M, B: Real); //irányvektoros egyenes
Begin
If M=0 Then Exit;
  NormEgyenes(M,-1,B);
End;

Procedure TfmLinalgDemo.NormEgyenes(A, B, C: Real); //normálvektoros egyenes
Const Dx=50;
      Dy=50;
Var Xh, Yh: Real;
Begin
If A*B=0 Then Exit;
  Xh:= Xk/Dx; Yh:= Yk/Dy;
With Canvas Do
Begin
    MoveTo(0, Yk+Round(Dy*(C-Xh*A)/B));
    LineTo(Xm, Yk+Round(Dy*(C+Xh*A)/B));
    MoveTo(Xk-Round(Dx*(C-Yh*B)/A), Ym);
    LineTo(Xk-Round(Dx*(C+Yh*B)/A), 0);
End;
End;

procedure TfmLinalgDemo.btStartClick(Sender: TObject);
begin
  KepTorles; btAlapClick(Sender);
  MatrixOlvas; TranszformKepre; SajatErtek;
  btAnimacio.Enabled:= True;
end;

procedure TfmLinalgDemo.tiIdozitoTimer(Sender: TObject);
begin
If Not Animal Then Exit;
With Canvas Do
Begin
    Pen.Color:= clWhite;
    MoveTo(Xk,Yk);
    LineTo(Xk + Round(D*Cos(AN*Ds*Pi/180)), Yk - Round(D*Sin(AN*Ds*Pi/180)));
    Pen.Color:= clYellow;
    MoveTo(Xk,Yk);
    LineTo(Xk + Round(A[1,1]*D*Cos(AN*Ds*Pi/180)+A[1,2]*D*Sin(AN*Ds*Pi/180)),
           Yk - Round(A[2,1]*D*Sin(AN*Ds*Pi/180)+A[2,2]*D*Sin(AN*Ds*Pi/180)));

    Inc(AN);

    Pen.Color:= clRed;
    MoveTo(Xk,Yk);
    LineTo(Xk + Round(D*Cos(AN*Ds*Pi/180)), Yk - Round(D*Sin(AN*Ds*Pi/180)));
    Pen.Color:= clBlue;
MoveTo(Xk,Yk);
    LineTo(Xk + Round(A[1,1]*D*Cos(AN*Ds*Pi/180)+A[1,2]*D*Sin(AN*Ds*Pi/180)),
           Yk - Round(A[2,1]*D*Sin(AN*Ds*Pi/180)+A[2,2]*D*Sin(AN*Ds*Pi/180)));
End;
end;

procedure TfmLinalgDemo.seSebesChange(Sender: TObject);
begin
  tiIdozito.Interval:= seSebes.Value;
end;

procedure TfmLinalgDemo.FormCreate(Sender: TObject);
begin
  Animal:= False; AN:= 0;
  tiIdozito.Interval:= seSebes.Value;
end;

procedure TfmLinalgDemo.btAnimacioClick(Sender: TObject);
begin
  Animal:= Not Animal;
With btAnimacio Do If Animal Then
  Caption:= 'Animáció Ki' Else Caption:= 'Animáció Be';
end;

procedure TfmLinalgDemo.btKilepesClick(Sender: TObject);
begin
  Close;
end;

end.