Ikerprím

Két prímszámot ikerprímnek nevezünk, ha különbségük 2. Ilyenek például: 3 és 5, 5 és 7, 11 és 13. A 3, 5 és 7 hármas ikerprímek. Több hármas ikerprím nem létezhet, hiszen három olyan szám, amelyek között 2 a különbség a következőképpen írható: 3k, 3k+2, 3k+4 vagy 3k+1, 3k+3, 3k+5, vagy 3k+2, 3k+4, 3k+6 (ahol k>2). Bármelyik szerinti felírás esetén a három számból az egyik osztható 3-al, azaz nem lehet mindegyike prím.

A program 1.000.000-ig kereste az ikerprímeket, melynek száma: 8240. A futási képek:

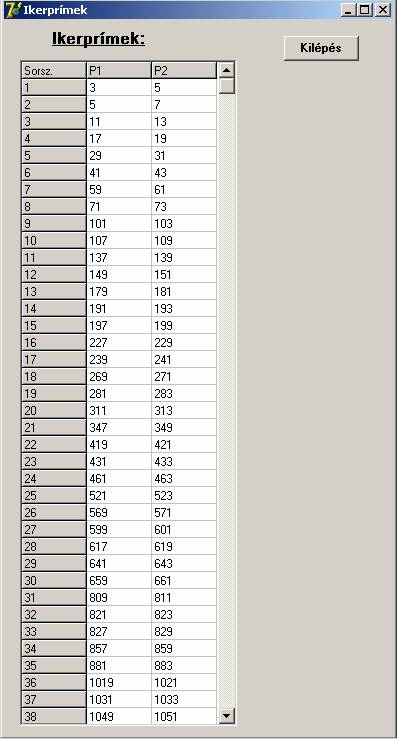
A program listája:

unit UIkerprimek;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes, Graphics,

Controls, Forms, Dialogs, Grids, StdCtrls;

type
TfmIkerprimek = class(TForm)
lbIkerprimek: TLabel;
sgTabla: TStringGrid;
btKilepes: TButton;
procedure btKilepesClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

var
fmIkerprimek: TfmIkerprimek;

implementation

{$R *.dfm}

procedure TfmIkerprimek.btKilepesClick(Sender: TObject);
begin
Close;
end;

Function Prime(S: Int64): Boolean;
Var J: Word;
Begin
Prime:= False; If S In [0,1] Then Exit;
Prime:= True; If S In [2,3] Then Exit;
Prime:= False; If (S Mod 6<>1) And (S Mod 6<>5) Then Exit;
Prime:= True;
For J:= 2 To S-1 Do If (S Mod J)=0 Then
Begin Prime:= False; Break End;
End;

procedure TfmIkerprimek.FormCreate(Sender: TObject);
Var I, N: LongInt;
begin
With sgTabla Do
Begin
Cells[0,0]:= 'Sorsz.';
Cells[1,0]:= 'P1';
Cells[2,0]:= 'P2';
    N:= 0;
For I:= 1 To 1000000 Do
If Prime(I) And Prime(I+2) Then
Begin
If RowCount<N+2 Then RowCount:= RowCount+1;
      Inc(N);
Cells[0,N]:= IntToStr(N);
Cells[1,N]:= IntToStr(I);
Cells[2,N]:= IntToStr(I+2);
End;
End;
end;

end.