Galton deszka
A Galton-deszka egy lejtősen
felállított, egyenlőszárúháromszög alakú deszka, melynek a felső csúcsától az
alaplapja felé golyókat lehet legurítani, melyek az útjukba eső akadályokon 1/2
– 1/2 valószínűséggel térnek el jobbra illetve balra, míg végül kis dobozokban
gyűlnek össze. Ha N darab eltérítési lehetőséggel találkozik, akkor N+1
dobozban gyűlnek össze golyók. Annak valószínűsége, hogy egy golyó a K. csatornába esik: (N alatt a K)/2n, azaz
binomiális eloszlást követ. A nagy számok törvénye szerint, ha N elég nagy,
akkor a binomiális eloszlás a normális eloszláshoz közelít.
Programunk a fent leírt folyamatot
szimulálja. A dobozokba esett golyókat egyre magasabb fehér téglalap jelzi.
Folyamatosan kiírja a középső öt doboz tartalmát, valamint az összes
felhasznált golyó számát. Ha az öt legtöbb golyót tartalmazó doboz valamelyike
tele van, leáll a szimuláció. Közben a program nem állítható meg. A futás
lassítása érdekében, egy
For
L:= 1 To 100 Do Pixels[200,20]:= clBlue;
sort
tartalmaz, melynek paraméterei az aktuális gép sebességéhez illesztendők.
A program startra kész állapotban:
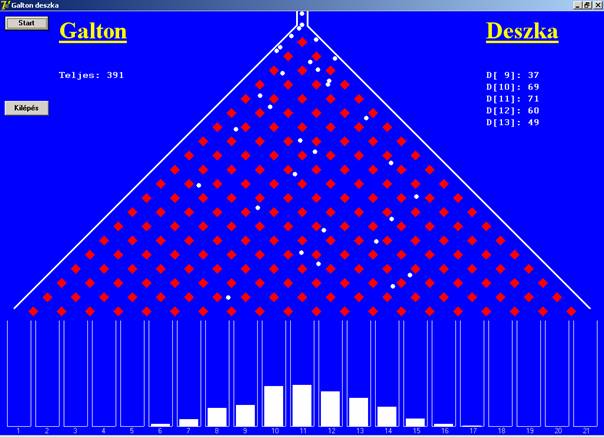
A program futási képe, amikor a 11. doboz tartalma 70 fölé
nőtt:
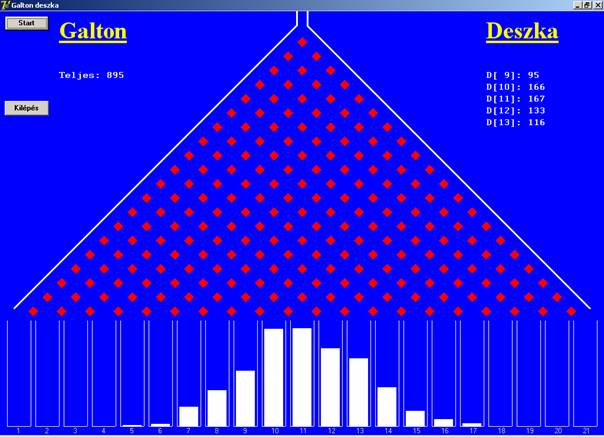
A futási kép az animáció befejeztével:
A program listája:
unit UGalton;
interface
uses
Windows, Messages, SysUtils, Variants, Classes,
Graphics, Controls, Forms, Dialogs, StdCtrls, ExtCtrls;
type
TfmGalton = class(TForm)
btStart: TButton;
btKilepes: TButton;
Procedure Deszka;
Procedure Animacio;
procedure FormCreate(Sender: TObject);
procedure FormPaint(Sender: TObject);
procedure btStartClick(Sender: TObject);
procedure btKilepesClick(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
TGolyo= Class
Fx, Fy, Fr, Fd: Integer;
Fm: Boolean;
Procedure Init(Ix, Iy, Ir: Integer);
Procedure Show;
Procedure Hide;
Procedure MoveRel(X, Y: Integer);
Function Moved: Boolean;
Procedure SetMove;
Function GetX: Integer;
Function GetY: Integer;
Function GetD: Integer;
Procedure SetD(D: Integer);
End;
Const N= 20; M= 32; Dx= 48; Dy= 24; Ex= -400; Ey= 20; R=4;
var
fmGalton: TfmGalton;
Xk, Yk: Integer;
Fg: Array[1..M+1] Of TGolyo;
D: Array[1..N+1] Of Integer;
implementation
{$R *.dfm}
Procedure TGolyo.Init(Ix, Iy, Ir: Integer);
Begin
Fx:= Ix; Fy:= Iy; Fr:= Ir; Fd:= 0; Fm:= False;
End;
Procedure TGolyo.Show;
Begin
With fmGalton.Canvas Do
Begin
Pen.Color:= clWhite;
Brush.Color:= clWhite;
Ellipse(Fx-Fr, Fy-Fr, Fx+Fr, Fy+Fr);
End;
End;
Procedure TGolyo.Hide;
Begin
With fmGalton.Canvas Do
Begin
Pen.Color:= clBlue;
Brush.Color:= clBlue;
Ellipse(Fx-Fr, Fy-Fr, Fx+Fr, Fy+Fr);
End;
End;
Procedure TGolyo.MoveRel(X, Y: Integer);
Begin
Hide; Fx:= Fx + X; Fy:= Fy + Y; Show;
End;
Function TGolyo.Moved: Boolean;
Begin
Moved:= Fm;
End;
Procedure TGolyo.SetMove;
Begin
Fm:= True;
End;
Function TGolyo.GetX: Integer;
Begin
GetX:= Fx;
End;
Function TGolyo.GetY: Integer;
Begin
GetY:= Fy;
End;
Function TGolyo.GetD: Integer;
Begin
GetD:= Fd;
End;
Procedure TGolyo.SetD(D: Integer);
Begin
Fd:= D;
End;
Procedure TfmGalton.Deszka;
Var I, J: Byte;
Ws: String;
Begin
With Canvas Do
Begin
Pen.Color:= clBlue;
Brush.Color:= clBlue;
Rectangle(0,0,2*Xk,2*Yk);
With Pen Do
Begin
Width:= 3;
Color:= clWhite;
End;
MoveTo(Xk-2*R-1,0); LineTo(Xk-2*R-1,6*R); LineTo(6*R,Xk-2*R-1);
MoveTo(Xk+2*R+1,0); LineTo(Xk+2*R+1,6*R); LineTo(2*Xk-6*R,Xk-2*R-1);
With Pen Do
Begin
Width:= 1;
Color:= clRed;
End;
Brush.Color:= clRed;
For I:= 1 To N Do For J:= I To N Do
Begin
If Odd(J) Then
Begin
MoveTo(Dx*(N-I)+Dx*(J Div 2)+Ex,Dy*J+Ey);
LineTo(Dx*(N-I)+Dx*(J Div 2)+Ex-2*R,Dy*J+Ey+2*R);
LineTo(Dx*(N-I)+Dx*(J Div 2)+Ex,Dy*J+Ey+4*R);
LineTo(Dx*(N-I)+Dx*(J Div 2)+Ex+2*R,Dy*J+Ey+2*R);
LineTo(Dx*(N-I)+Dx*(J Div 2)+Ex,Dy*J+Ey);
FloodFill(Dx*(N-I)+Dx*(J Div 2)+Ex,Dy*J+Ey+1,clRed,fsBorder);
End Else
Begin
MoveTo(Dx*(N-I)+Dx*(J Div 2)-Dx Div 2+Ex,Dy*J+Ey);
LineTo(Dx*(N-I)+Dx*(J Div 2)-Dx Div 2+Ex-2*R,Dy*J+Ey+2*R);
LineTo(Dx*(N-I)+Dx*(J Div 2)-Dx Div 2+Ex,Dy*J+Ey+4*R);
LineTo(Dx*(N-I)+Dx*(J Div 2)-Dx Div 2+Ex+2*R,Dy*J+Ey+2*R);
LineTo(Dx*(N-I)+Dx*(J Div 2)-Dx Div 2+Ex,Dy*J+Ey);
FloodFill(Dx*(N-I)+Dx*(J Div 2)-Dx Div 2+Ex,Dy*J+Ey+1,clRed,fsBorder);
End;
End;
Pen.Color:= clWhite;
Brush.Color:= clBlue;
For I:= 1 To N+1 Do
Begin
MoveTo(I*Dx-9*R,(N+2)*Dy-R);
LineTo(I*Dx-9*R,2*Yk-15);
MoveTo(I*Dx+R,(N+2)*Dy-R);
LineTo(I*Dx+R,2*Yk-15);
MoveTo(I*Dx-9*R,2*Yk-15);
LineTo(I*Dx+R,2*Yk-15);
Font.Color:= clBtnFace;
Str(I,Ws); TextOut(I*Dx-5*R, 2*Yk-14, Ws);
End;
With Font Do
Begin
Name:= 'Times New Roman';
Color:= clYellow;
Size:= 30;
Style:= [fsBold,fsUnderLine];
End;
TextOut(100,10,'Galton'); TextOut(2*Xk-200,10,'Deszka');
With Font Do
Begin
Size:= 12;
Name:= 'courier';
Style:= [fsBold];
End;
End;
For I:= 1 To M+1 Do
Begin
Fg[I]:= TGolyo.Create;
Fg[I].Init(Xk,R,R); Fg[1].Show;
End;
Fg[1].SetMove;
End;
procedure TfmGalton.btKilepesClick(Sender: TObject);
begin
Close;
end;
procedure TfmGalton.FormCreate(Sender: TObject);
begin
Xk:= ClientWidth Div 2;
Yk:= ClientHeight Div 2;
Randomize;
end;
Procedure TfmGalton.Animacio;
Var I, K: Byte;
L: LongInt;
S, SM: Word;
Ws: String;
Begin
I:= 1; S:= 0; SM:= 2*Yk-(N+3)*Dy;
Repeat
With Fg[I] Do If Moved Then With Canvas Do
Begin
MoveRel(GetD,1);
If GetY Mod Dy=0 Then
Begin
SetD(1-2*Random(2));
Fg[I+1].SetMove;
End;
If GetY>(N+1)*Dy Then
Begin
K:= ((GetX-5*R) Div Dx)+1; Inc(D[K]);
Brush.Color:= clWhite;
Pen.Color:= ClWhite;
Rectangle((K-1)*Dx+4*R,2*Yk-2-D[K]-12,(K-1)*Dx+Dx,2*Yk-14);
Hide; Init(Xk,R,R); SetMove; Show; Inc(S);
Pen.Color:= clBlue;
Brush.Color:= clBlue;
Font.Color:= clWhite;
Rectangle(100,100,200,210);
Str(S,Ws); TextOut(100,100,'Teljes: '+Ws);
Str(D[ 9],Ws); TextOut(2*Xk-200,100,'D[ 9]: '+Ws);
Str(D[10],Ws); TextOut(2*Xk-200,120,'D[10]: '+Ws);
Str(D[11],Ws); TextOut(2*Xk-200,140,'D[11]: '+Ws);
Str(D[12],Ws); TextOut(2*Xk-200,160,'D[12]: '+Ws);
Str(D[13],Ws); TextOut(2*Xk-200,180,'D[13]: '+Ws);
End;
For L:= 1 To 100 Do Pixels[200,20]:= clBlue;
End;
Inc(I); If I>M Then I:= 1;
Until (D[9]>SM) Or (D[10]>SM) Or
(D[11]>SM) Or (D[12]>SM) Or (D[13]>SM);
For I:= 1 To M+1 Do Fg[I].Hide;
End;
procedure TfmGalton.btStartClick(Sender: TObject);
begin
Animacio;
end;
procedure TfmGalton.FormPaint(Sender: TObject);
begin
Deszka;
end;
end.