SZAKDOLGOZAT
Görbe Mihály
I
Kossuth Lajos Tudományegyetem
Matematika Intézete
A GLOBÁLIS DIFFERENCIÁLGEOMETRIA
NÉHÁNY
ALAPFOGALMA
Készítette: Témavezető:
Görbe Mihály Szilasi József
v.évf. mat-fiz. szakos h.
Debrecen
1977
II
Köszönetet mondok Szilasi
József tanársegéd úrnak szakdolgozatom elkészítése során nyújtott segítségéért.
III
Előszó
Ebben a dolgozatban – alapfogalmainak tárgyalása révén
– bevezetést kívánunk nyújtani a globális differenciálgeometriába.
Célunk a differenciálható sokaság definíciójának
megadásán túlmenően, hogy foglalkozzunk a sokaság érintőterével,
érintőnyalábjával, továbbá az, hogy a Riemann sokaság
és Finsler sokaság definiálásával alapot nyújtsunk a
metrikus differenciálgeometriai terek tárgyalásához.
Az első fejezetben, mely bevezető jellegű, az Rn
halmaz euklideszi, affin és differenciálható
struktúrájával foglalkozunk, mintegy szemléleti előkészítésként a következő
fejezetek számára.
A második részben a bevezetésben megismert
differenciálható struktúra messzemenő, a differenciálgeometria számára
kielégítő általánosítását tárgyaljuk. Így jutunk a differenciálható sokaság
fogalmához. Definiáljuk továbbá a függvények és leképezések
differenciálhatóságát.
Az utolsó két fejezetben további globális alapfogalmakat
definiálunk, úgymint: érintővektor, érintőtér, vektormező, derivációk,
érintőnyaláb, principális nyaláb, Riemann sokaság, Finsler sokaság.
A dolgozatban szereplő fogalmak megértéséhez
nélkülözhetetlen a topológia, lineáris algebra, algebra, analízis, elemi
geometria alapvető fogalmainak ismerete, melyet a továbbiakban fel is
tételezünk.
IV
Tartalom
I. Bezetés 1.
1.
Az n-dimenziós
euklideszi tér 2.
2.
Az affin tér 8.
4.
Az euklideszi, affin és lineáris tér kapcsolata 10.
II. Differenciálható sokaságok 17.
3.
Differenciálható leképezések, differenciálható görbék 27.
III. Érintővektorok 30.
1.
Az érintővektor 31.
2.
Az érintőtér 32.
3.
Vektormezők, derivációk 35.
4.
Az érintő nyaláb 41.
IV. Riemann
sokaság 45.
2.
Finsler sokaság 49.
Felhasznált irodalom 50.
1. oldal
I. Bevezetés
Ebben az előkészítő fejezetben különféle, egymással
szoros kapcsolatban lévő struktúrákkal látjuk el az
![]()
halmazt,
melyet a rendezett valós számennesek halmazának
nevezünk.
Így jutunk az euklideszi térhez, amely valamennyi
további meggondolásunk kiindulópontjául szolgál. Ezen kívül Rn -et topológikus térré tesszük, és
ezen differenciálható struktúrát adunk meg. Ez utóbbi konstrukció a következő
fejezetben messzemenő általánosítást nyer. Röviden, csak az eredmények
közlésével foglalkozunk a Vn érintőterével, valamint az Rn -en adott különböző struktúrák kapcsolatával.
2. oldal
1. Az n-dimenziós
euklideszi tér
Ebben a részben az n-dimenziós euklideszi térrel
foglalkozunk, melynek fontosságát misem bizonyítja jobban, mint az, hogy a
továbbiakban vizsgálataink során végig szerepet játszik. Foglalkozunk továbbá
az ezen a téren adott függvények differenciálhatóságával, s megemlítjük az
inverz függvény tételt.
1. Tétel: Legyen Rn a rendezett valós számennesek
halmaza. Ha
![]()
akkor
a
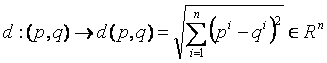
függvény
az Rn
metrikája.
1. Definíció: Az (Rn, d)
= En metrikus teret n-dimenziós
euklideszi térnek nevezzük. Az Rn halmaz p
= (p1, p2,…, pn)
elemét az En
tér pontjának, a p1, p2,…,
pn számokat a p pont koordinátáinak nevezzük.
Az En teret tegyük topológikus
térré a d metrika által indukált
topológiával.
2. Definíció: Az En tér olyan önmagára való ![]() homeomorfizmusát, mely a tér két pontjának a távolságát invariánsan hagyja, azaz
homeomorfizmusát, mely a tér két pontjának a távolságát invariánsan hagyja, azaz
![]()
igaz
minden ![]() -re, az En
tér egy mozgásának nevezzük. Az En tér mozgásainak halmaza csoportot alkot,
melyet E(n) -nel fogunk jelölni
-re, az En
tér egy mozgásának nevezzük. Az En tér mozgásainak halmaza csoportot alkot,
melyet E(n) -nel fogunk jelölni
Ezen definíciók alapján az euklideszi geometria teljes
egészében felépíthető, eredményei tárgyalhatók.
3. oldal
3. Definíció: Legyen ![]() és
és ![]() . Legyen
. Legyen
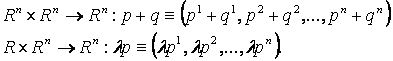
Ezekkel
a vektortér műveletekkel az Rn egy n-dimenziós vektortér az R felett. Ilyen esetben En elemeit vektoroknak is
tekinthetjük.
4. Definíció: Legyen a p =
(p1, p2,…, pn)
az En
egy pontja. Legyen xi(p) = pi
(i = 1, 2,…, n). Az x1, x2,…,
xn az En -nek
folytonos függvényei, melyet koordinátafüggvényeknek nevezünk. Az (x1, x2,…, xn) függvényennest
pedig az En
standard koordinátarendszerének hívjuk.
Most az En -en definiált függvények differenciálhatóságával
foglalkozunk.
5. Definíció: Legyen az f =
f(x1(p), x2(p),…, xn(p))
függvény az En
egy U nyílt halmazán definiálva és
legyen ![]() . Legyen q a 0 =
(0, 0,…, 0) pont környezetében. Ha az f(p+q)
- f(p) különbség
. Legyen q a 0 =
(0, 0,…, 0) pont környezetében. Ha az f(p+q)
- f(p) különbség
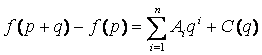
alakban
írható, ahol Ai
egy q -tól
független konstans, C(q) pedig a q egy olyan függvénye, hogy ![]() esetén a
esetén a 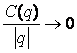 , akkor azt mondjuk, hogy az f függvény a p -ben totálisan differenciálható.
, akkor azt mondjuk, hogy az f függvény a p -ben totálisan differenciálható.
4. oldal
2. Tétel: Ha az f
függvény totálisan differenciálható a p
pontban, akkor minden xi
változója szerint is differenciálható és
 .
.
6. Definíció: Ha az f
függvény az ![]() minden pontjában
totálisan differenciálható, akkor az f
az U-n totálisan
differenciálható.
minden pontjában
totálisan differenciálható, akkor az f
az U-n totálisan
differenciálható.
7. Definíció: Legyen f
egy, az En
egy U nyílt halmazán definiált
függvény. Ha az f az U minden pontjában minden xi
változója szerint differenciálható és ezen
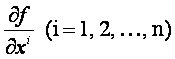
parciális
deriváltak az U folytonos
függvényei, akkor f -et folytonosan deriválható függvénynek, vagy C1 osztályú
függvénynek nevezzük.
8. Definíció: Legyen f
egy, az En
egy nyílt halmazán definiált függvény. Ha az r olyan pozitív egész szám, hogy az f -nek az U minden pontjában az r -ed rendű
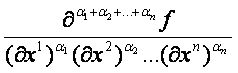 (
(![]()
![]() )
)
parciális
deriváltak mind léteznek és az U -n
folytonosak, akkor f -et r
-szeresen folytonosan differenciálható függvénynek, vagy Cr
osztályú függvénynek nevezzük.
5. oldal
9. Definíció: Ha az En egy U
nyílt részhalmazán értelmezett f
függvény minden pozitív r egész
esetén Cr
osztályú, akkor C∞ osztályú függvénynek nevezzük.
A folytonos függvényeket az előzőek szerint joggal C0 osztályú
függvényeknek nevezhetjük.
10. Definíció: Ha az f az
![]() C∞ osztályú
függvénye és minden
C∞ osztályú
függvénye és minden ![]() -ra a
-ra a

hatványsor
abszolút konvergens és egyenletesen konvergál az f(x1, x2,…, xn)-hez a p egy
elég kis környezetében, ahol
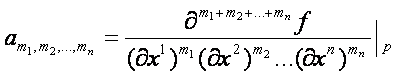
akkor f -et analitikus függvénynek, vagy ![]() osztályú függvénynek
nevezzük.
osztályú függvénynek
nevezzük.
11. Definíció: Legyen φ
az En U nyílt halmazának egy En -be
való leképezése. Legyen
![]()
Ekkor
minden φi
egy U -n definiált függvény. Ha
minden φi Cr osztályú, akkor azt mondjuk, hogy φ egy Cr osztályú
leképezés.
12. Definíció: Ha a φ
az En U nyílt halmazának egy C1 osztályú leképezése En-re,
akkor minden ![]() pontra és
pontra és ![]() vektorra létezik a
vektorra létezik a
6. oldal
![]()
határérték
és egyenlő
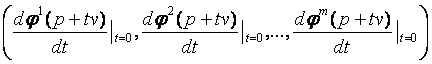 -val.
-val.
Ezt
a határértéket (dφ)p(v)-vel jelöljük és a φ
leképezés p -beli
v irányra vett deriváltjának
nevezzük.
A (dφ)p :
v → (dφ)p (v) megfeleltetés
az En
vektortérnek egy lineáris leképezése az Em vektortérre. Így
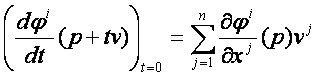
Ha
az En
és Em
vektorait oszlopvektoroknak írjuk, akkor

ahol
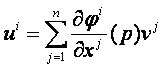 (i = 1, 2, …, m)
(i = 1, 2, …, m)
Jelöljük
a

m x n -es
mátrixot (Jφ)p
-vel. Ezt a φ leképezés p -beli Jacobi mátrixának
nevezzük. Ha m=n, akkor a (Jφ)p
négyzetes mátrix, és determinánsa:
7. oldal
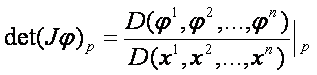
Melyet
a φ leképezés p -beli Jacobi determinánsának nevezünk.
13. Definíció: Legyen φ
az En
egy U nyílt halmazának az En
egy V nyílt részhalmazára való
egy-egyértelmű leképezése. Ha a φ
és φ-1 is Cr
osztályú leképezés, akkor φ -t Cr
osztályú diffeomorf leképezésnek nevezzük.
Egy C0
osztályú diffeomorf leképezés nyilván csak homeomorf leképezés.
3. Tétel: (Inverz függvény tétel) Legyen φ az En
egy U nyílt halmazának az En -be való Cr (1≤r≤∞) osztályú
leképezése. Ha a φ leképezésnek
a Jacobi determinánsa az U egy p0
pontjában nem zérus, akkor a φ
az En p0 pontja egy környezetének
az En
egy φ(p0) pontja
környezetére való Cr
diffeomorfizmusa, azaz létezik a p0 -nak és a φ(p0) -nak egy olyan U0 ![]() illetve V0 környezete, hogy ha a φ -t megszorítjuk az U0 -ra,
akkor a φ az U0 -nak
V0 -ra
való Cr
diffeomorfizmusa.
illetve V0 környezete, hogy ha a φ -t megszorítjuk az U0 -ra,
akkor a φ az U0 -nak
V0 -ra
való Cr
diffeomorfizmusa.
8. oldal
2. Az affin
tér
1. Definíció: Vegyük az (Rn, d) = En
n-dimenziós
euklideszi teret. Tekintsünk el a tér metrikájától, de tartsuk meg a d által indukált topológiát, az egyenes
és a párhuzamosság fogalmát. Ekkor az An -nel
jelölt n-dimenziós
affin térhez jutunk.
Az An n-dimenziós affin térben beszélhetünk folytonosságról, egyenesekről és
azok párhuzamosságáról, de nem beszélhetünk két pont távolságáról.
2. Definíció: Az An egy olyan önmagára való homeomorfizmusát,
mely egyeneseknek egyeneseket feleltetnek meg, az An tér affinitásának
nevezzük. Az An
affinitásainak halmaza csoportot alkot, melyet A(n) -nel fogunk jelölni.
9. oldal
1. Definíció: Vegyük az En teret és rajta a d metrikája által indukált topológiát, majd tekintsünk el a d metrikától. Az Rn vektortér erre a
topológiára nézve topológikus vektortér. Ezt a topológikus vektorteret n-dimenziós
lineáris térnek nevezzük és Vn -el jelöljük.
2. Definíció: A Vn topológikus
vektortérnek olyan önmagára való
£: Vn
→ Vn![]()
![]()
homeomorfizmusát, mely a Vn
vektortér műveleteit változatlanul hagyja, azaz
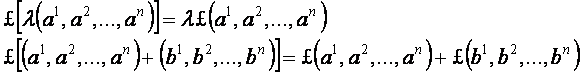
a Vn
egy nemszinguláris lineáris transzformációjának
nevezzük. A Vn
nemszinguláris transzformációinak halmaza csoportot
alkot, melyet általános lineáris csoportnak nevezünk és GL(n) -el jelölünk.
10. oldal
4. Az euklideszi, affin
és lineáris tér kapcsolata
1. Definíció: Legyen ![]() . Azt fogjuk mondani a Vn -nek az En -re való
. Azt fogjuk mondani a Vn -nek az En -re való ![]() homeomorfizmusáról,
mely kielégíti a
homeomorfizmusáról,
mely kielégíti a ![]() feltételt, hogy a Vn -et
a
feltételt, hogy a Vn -et
a ![]() ponthoz kapcsolja.
ponthoz kapcsolja.
A definícióban szereplő ![]() homeomorfizmus
révén a Vn
additív csoportja az En
-en úgy hat, mint egy homeomorfizmus
csoport, azaz a
homeomorfizmus
révén a Vn
additív csoportja az En
-en úgy hat, mint egy homeomorfizmus
csoport, azaz a
![]() ,
,
az
En
olyan homeomorfizmusai, amelyek kielégítik a ![]() relációt. Ha ez a homeomorfizmus csoport E(n)
-beli elemekből áll, akkor ezeket a homeomorfizmusokat az En
transzlációinak nevezzük. Egy ilyen kapcsolatot létesítő
relációt. Ha ez a homeomorfizmus csoport E(n)
-beli elemekből áll, akkor ezeket a homeomorfizmusokat az En
transzlációinak nevezzük. Egy ilyen kapcsolatot létesítő ![]() homeomorfizmusról
azt mondjuk, hogy a Vn
-et affin módon
kapcsolja az En p pontjához. Azt is mondhatjuk, hogy
ebben az esetben a Vn
identifikálva (azonosítva) van En -nel. Ha a
homeomorfizmusról
azt mondjuk, hogy a Vn
-et affin módon
kapcsolja az En p pontjához. Azt is mondhatjuk, hogy
ebben az esetben a Vn
identifikálva (azonosítva) van En -nel. Ha a ![]() és
és ![]() affin
módon kapcsolja a Vn
-et az En -hez, akkor a
affin
módon kapcsolja a Vn
-et az En -hez, akkor a ![]() a Vn -nek egy nemszinguláris lineáris
transzformációja.
a Vn -nek egy nemszinguláris lineáris
transzformációja.
2. Definíció: Ha
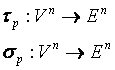
esetén
létezik olyan ![]() nemszinguláris
lineáris transzformáció, hogy
nemszinguláris
lineáris transzformáció, hogy
11. oldal
![]()
akkor
azt mondjuk, hogy ![]() és
és ![]() ekvivalensek.
ekvivalensek.
Tekintsük a ![]() homeomorfizmusoknak
az előző ekvivalencia relációra nézve az ekvivalencia osztályait. Legyenek
homeomorfizmusoknak
az előző ekvivalencia relációra nézve az ekvivalencia osztályait. Legyenek ![]() és
és ![]() egy osztályban. Akkor
és csak akkor identifikálja a
egy osztályban. Akkor
és csak akkor identifikálja a ![]() a Vn -et En
-nel, ha
a Vn -et En
-nel, ha ![]() is azt teszi, s ekkor
a
is azt teszi, s ekkor
a ![]() és a
és a ![]() az En ugyanazon
transzláció csoportját határozza meg. Így az identifikáció lényegileg egyértelmű,
hiszen csak egyetlen ekvivalencia osztálybeli homeomorfizmusok
révén jöhet létre.
az En ugyanazon
transzláció csoportját határozza meg. Így az identifikáció lényegileg egyértelmű,
hiszen csak egyetlen ekvivalencia osztálybeli homeomorfizmusok
révén jöhet létre.
Tétel: Kapcsolja a ![]() homeomorfizmusok
egy {
homeomorfizmusok
egy {![]() } családja a Vn -et affin módon az En pontjaihoz, azaz minden
} családja a Vn -et affin módon az En pontjaihoz, azaz minden ![]() -hez
létezik egy olyan {
-hez
létezik egy olyan {![]() } -beli homeomorfizmus,
hogy az a Vn
-et affin módon kapcsolja
az En -beli p ponthoz.
Ha a
} -beli homeomorfizmus,
hogy az a Vn
-et affin módon kapcsolja
az En -beli p ponthoz.
Ha a ![]() egy mozgás, akkor a
egy mozgás, akkor a
![]()
minden
![]() -re egy nemszinguláris lineáris transzformáció.
-re egy nemszinguláris lineáris transzformáció.
Ebben a részben tárgyalt tételek és definiciók mindegyike megfogalmazható úgy is, hogy az En -et An
-el, E(n) -et
A(n) -el (mozgást affinitással)
cseréljük ki. Az így nyert állítások a Vn és An kapcsolatát tükrözik.
A fejezet célja az volt, hogy rámutasson a Vn -nek az euklideszi illetve affin
struktúrákkal való kapcsolatára. Elmondhatjuk tehát, hogy a Vn hozzácsatolható En (ill. An) -hez oly módon, hogy az En egy mozgása (ill.
az An
egy affinítása) a Vn -nek egy nemszinguláris lineáris
transzformációját indukálják. Ezáltal az An mozgásainak (ill.
az An
affinitásainak) tulajdonságai a Vn lineáris transzformációiban tükröződnek.
Azokat a tulajdonságokat, amelyek a mozgáscsoporttal
szemben invariánsak metrikus vagy mozgás-invariánsoknak, azokat
pedig, amelyek az affinitások csoportjával szemben invariánsak affin invariánsoknak nevezzük.
Röviden a továbbiakban azt is mondhatjuk, hogy az
identifikálás révén a Vn
-et euklideszi illetve affin
struktúrával láttuk el.
13. oldal
Legyen a Vn identifikálva az En -nel a ![]() homeomorfizmus
segítségével. Ha
homeomorfizmus
segítségével. Ha ![]() , akkor a
, akkor a ![]() -ben
szereplő
-ben
szereplő ![]() számokat az a koordinátáinak
nevezzük. Definiáljuk a
számokat az a koordinátáinak
nevezzük. Definiáljuk a ![]() segítségével a Vn -en értelmezett függvények és leképezések
differenciálhatóságát a következőképpen:
segítségével a Vn -en értelmezett függvények és leképezések
differenciálhatóságát a következőképpen:
1. Definíció: Legyen U a
Vn
-nek egy nyílt halmaza. Azt mondjuk, hogy az
f : U → R
függvény
differenciálható az U -n, ha az
![]()
függvény
a ![]() minden pontjában
rendelkezik a q1, q2,
…, qn koordináták szerinti parciális
deriváltakkal tetszőleges rendben.
minden pontjában
rendelkezik a q1, q2,
…, qn koordináták szerinti parciális
deriváltakkal tetszőleges rendben.
Ez a definíció független a ![]() homeomorfizmus
megválasztásától.
homeomorfizmus
megválasztásától.
2. Definíció: Legyen U
és Vn
-nek egy nyílt halmaza és tekintsük a ![]() leképezést. Azt
mondjuk, hogy a
leképezést. Azt
mondjuk, hogy a ![]() leképezés az U -n differenciálható, minden olyan
g függvény esetén, amely
differenciálható Vm
-nek valamely W
nyílt halmazán, a
leképezés az U -n differenciálható, minden olyan
g függvény esetén, amely
differenciálható Vm
-nek valamely W
nyílt halmazán, a ![]() függvény
differenciálható
függvény
differenciálható ![]() -n.
-n.
14. oldal
Ha a ![]() egy olyan bijektív, differenciálható leképezés, melynek
egy olyan bijektív, differenciálható leképezés, melynek ![]() inverze is
differenciálható, akkor
inverze is
differenciálható, akkor ![]() -t diffeomorfizmusnak
nevezzük. A diffeomorfizmusok a differenciálható
függvények halmazát invariánsan hagyják. A Vn diffeomorfizmusai csoportot alkotnak.
-t diffeomorfizmusnak
nevezzük. A diffeomorfizmusok a differenciálható
függvények halmazát invariánsan hagyják. A Vn diffeomorfizmusai csoportot alkotnak.
Ha részletesen megvizsgálnánk azt a problémát, hogy
miként lehet a Vn
-et az En pontjaihoz – az előző részben tárgyaltak
mintájára – hozzákapcsolni olymódon, hogy az En egy diffeomorfizmusa a Vn egy nemszinguláris
lineáris transzformációját indukálják, azt kapnánk, hogy ez nem lehetséges.
Általában egy vektortérben a differeciálható leképezéseknek
csak egy pont környezetében való, tehát lokális viselkedése tükröződhet.
Annak a vektortérnek a definiálására térünk most rá,
amelyben a diffeomorfizmus egy nem szinguláris
lineáris transzformációt indukál, ez lesz a Vn érintőtere.
3. Definíció: Legyen I =
(-1, 1). A ![]() differenciálható
leképezést a Vn
egy differenciálható görbéjének nevezzük. Ha
differenciálható
leképezést a Vn
egy differenciálható görbéjének nevezzük. Ha ![]() , akkor azt mondjuk, hogy a
, akkor azt mondjuk, hogy a ![]() átmegy a v -n.
átmegy a v -n.
Legyen ![]() . Legyen G a v -n átmenő differenciálható görbék
halmaza, F a v környezetében definiált differenciálható függvények halmaza. Ha
. Legyen G a v -n átmenő differenciálható görbék
halmaza, F a v környezetében definiált differenciálható függvények halmaza. Ha ![]() ,
, ![]() , akkor
, akkor ![]() a t -nek differenciálható függvénye, ha t elegendően kicsi. Legyen
a t -nek differenciálható függvénye, ha t elegendően kicsi. Legyen ![]() . Két G -beli
. Két G -beli ![]() és
és ![]() görbét ekvivalensnek
mondjuk, ha
görbét ekvivalensnek
mondjuk, ha
15. oldal
![]()
igaz
minden ![]() -re. Hasonlóan: két F -beli f1 és f2 függvényt ekvivalensnek mondunk, ha
-re. Hasonlóan: két F -beli f1 és f2 függvényt ekvivalensnek mondunk, ha
![]()
igaz
minden ![]() -re.
-re.
4. Definíció: A G -nek az előző ekvivalencia relációra vonatkozó ekvivalencia
osztályait a Vn
v -beli érintővektorainak,
s ezek összességét a Vn
v -beli érintőterének
nevezzük és Tv(Vn) -vel jelöljük.
5. Definíció: Az F -nek az előző ekvivalencia relációra vonatkozó ekvivalencia
osztályait v -beli
differenciáloknak vagy duális érintővektoroknak, ezek összességét
v -beli duális
érintőtérnek nevezzük és ![]() -vel
jelöljük. (A differenciálokat df -vel is fogjuk jelölni.)
-vel
jelöljük. (A differenciálokat df -vel is fogjuk jelölni.)
A Tv(Vn) és ![]() vektorterek egymás
duálisai és dimenziójuk n.
vektorterek egymás
duálisai és dimenziójuk n.
Az ![]() -t a
-t a ![]() görbe érintővektorának
nevezzük, ha az
görbe érintővektorának
nevezzük, ha az
![]()
relációt
teljesíti.
Legyen
![]() az U -nak a Vn
-be való leképezése, akkor
az U -nak a Vn
-be való leképezése, akkor ![]() egy
egy ![]() -re illeszkedő görbe.
(ábra)
-re illeszkedő görbe.
(ábra)
16. oldal
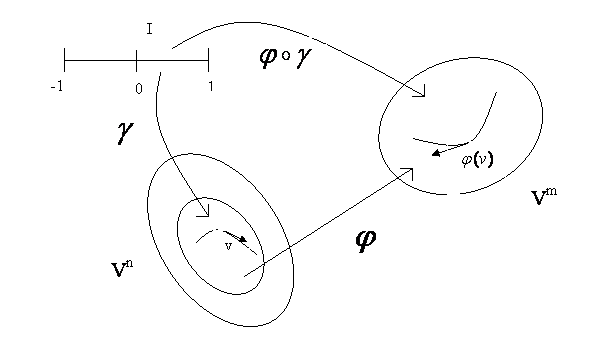
Legyen
![]() érintővektora) ≡ a
érintővektora) ≡ a ![]() érintővektora.
érintővektora.
Ekkor
a
![]()
egy
lineáris leképezés lesz a v -beli és ![]() -beli
érintőterek között. Ehhez hasonlóan
-beli
érintőterek között. Ehhez hasonlóan ![]() és
és ![]() duális érintőterek
között is differenciálható egy
duális érintőterek
között is differenciálható egy
![]()
leképezés,
mely szintén lineáris.
A ![]() és
és ![]() lesznek azok a
lineáris leképezések, melyekben megfigyelhetők a
lesznek azok a
lineáris leképezések, melyekben megfigyelhetők a ![]() leképezés
tulajdonságai. Általában, ha a
leképezés
tulajdonságai. Általában, ha a ![]() egy diffeomorfizmus, akkor a
egy diffeomorfizmus, akkor a ![]() és
és ![]() nemszinguláris
lineáris transzformációk.
nemszinguláris
lineáris transzformációk.
Mivel a Vn mozgásai és affinitásai egyben diffeomorfizmusok is, megállapítható, hogy a Vn
differenciálható struktúrája bővebb mint az affin, és
az bővebb mint az euklideszi struktúrája.
17. oldal
II. Differenciálható sokaságok
Ebben a fejezetben az előző fejezet
általánosításaként, egy topológikus téren, méghozzá Hausdorff-féle topológikus téren
fogunk differenciálható struktúrát definiálni, így jutunk a differenciálható
sokaság fogalmához. Láthatjuk majd, hogy ez a fogalomalkotás mennyire segíti a topológikus terünkön definiált függvények
differenciálhatóságának definícióját. Ez a segítség bizonyos egyértelműségben
és függetlenségben jelentkezik majd. Ebben a fejezetben tárgyaljuk a
leképezések differenciálhatóságát is.
18. oldal
1. Definíció: Legyen M
egy Hausdorff-féle topológikus
tér. Ha az M minden pontjának
létezik olyan környezete, mely homeomorf az En
egy nyílt halmazával, akkor az M -et n-dimenziós
topológikus sokaságnak nevezzük.
2. Definíció: Legyen az M egy n-dimenziós topológikus
sokaság. Legyen az U az M -nek egy
olyan nyílt halmaza, hogy a
![]()
leképezés
egy homeomorfizmus, ahol az E az En
egy nyílt halmaza. Ekkor a ![]() párt az M egy koordináta környezetének
nevezzük.
párt az M egy koordináta környezetének
nevezzük.
3. Definíció: Legyen az M
egy n-dimenziós
topológikus sokaság és legyen ![]() egy koordináta
környezete. Ha a p az U -nak egy
pontja, akkor
egy koordináta
környezete. Ha a p az U -nak egy
pontja, akkor ![]() az En egy pontját
jelenti, azaz a
az En egy pontját
jelenti, azaz a ![]() egy valós számennes. Jelöljük a
egy valós számennes. Jelöljük a ![]() i -edik koordinátáját xi(p) -vel.
Ekkor
i -edik koordinátáját xi(p) -vel.
Ekkor
![]()
a.) Mivel a ![]() folytonos leképezés,
minden xi
az U -n egy valósértékű folytonos
függvény.
folytonos leképezés,
minden xi
az U -n egy valósértékű folytonos
függvény.
19. oldal
b.) Mivel a ![]() egy-egyértelmű
leképezés,
egy-egyértelmű
leképezés, ![]() esetén abból, hogy xi(p)=xi(q)
(i = 1, 2, …, n), az következik, hogy p=q.
Így az U minden p pontja egyértelműen meghatároz egy (x1(p), x2(p), …, xn(p))
valós számennest.
esetén abból, hogy xi(p)=xi(q)
(i = 1, 2, …, n), az következik, hogy p=q.
Így az U minden p pontja egyértelműen meghatároz egy (x1(p), x2(p), …, xn(p))
valós számennest.
Ha
a p az U egy pontja, akkor az (x1(p),
x2(p), …, xn(p)) valós számennest a p
pont ![]() koordináta
környezetére vonatkozó lokális koordinátáinak nevezzük.
koordináta
környezetére vonatkozó lokális koordinátáinak nevezzük.
Az
U xi, (i = 1, 2, …, n) valós folytonos
függvényeit koordinátafüggvényeknek, az ezekből álló (x1, x2, …, xn) függvényennest
az ![]() lokális
koordinátarendszerének nevezzük.
lokális
koordinátarendszerének nevezzük.
(Összegezve:
az U halmaz egy p pontjának az ![]() koordinátakörnyezetre
vonatkozó lokális koordinátái egyenlők a
koordinátakörnyezetre
vonatkozó lokális koordinátái egyenlők a ![]() En -beli koordinátáival.)
En -beli koordinátáival.)
Megjegyezzük,
hogy a lokális jelző arra utal, hogy koordináták az M -nek csak egy nyílt részhalmazán vannak
bevezetve. Csak akkor adható meg egy olyan lokális koordinátarendszer, mely a
teljes M -en
definiálva van, ha az M homeomorf az En egy nyílt halmazával, azaz magával az En -nel. Nyilvánvaló, hogy ilyen koordinátarendszer egy
általános Hausdorff-féle topológikus
tér esetén nem létezik, innen ered a lokális elnevezés.
20. oldal
4.
Definíció: Legyen M egy n-dimenziós topológikus
sokaság. Legyen A és ![]() indexek halmaza.
Legyen
indexek halmaza.
Legyen ![]() az M egy olyan nyílt lefedése, hogy a
az M egy olyan nyílt lefedése, hogy a
![]()
minden
![]() esetén egy homeomorfizmus, ahol az
esetén egy homeomorfizmus, ahol az ![]()
![]() az En egy nyílt halmaza.
Az
az En egy nyílt halmaza.
Az ![]() koordináta környezetek
együttesét egy koordináta környezet rendszernek, vagy atlasznak
nevezzük és
koordináta környezetek
együttesét egy koordináta környezet rendszernek, vagy atlasznak
nevezzük és ![]() -val
jelöljük.
-val
jelöljük.
Legyen
M egy n-dimenziós
topológikus sokaság és ![]() ennek egy atlasza.
Legyen
ennek egy atlasza.
Legyen ![]() olyan, hogy benne van
az
olyan, hogy benne van
az ![]()
![]() és
és ![]() koordinátakörnyezetekben is. Ekkor a p két koordinátarendszernek is eleme.
Vizsgáljuk meg a két koordinátarendszer közötti kapcsolatot. (ábra)
koordinátakörnyezetekben is. Ekkor a p két koordinátarendszernek is eleme.
Vizsgáljuk meg a két koordinátarendszer közötti kapcsolatot. (ábra)
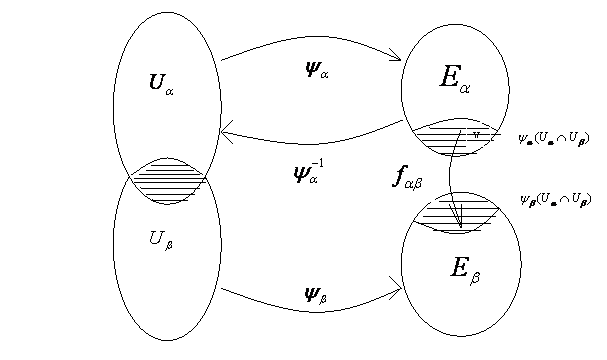
Az
![]() (1)
(1)
21. oldal
a ![]() -nak
nyilván egy homeomorfizmusa
-nak
nyilván egy homeomorfizmusa ![]() -re.
-re.
Ha
(u)=(u1, u2, …, un),
akkor
![]()
Így
![]() az (u1, u2,
…, un) változók folytonos függvénye.
az (u1, u2,
…, un) változók folytonos függvénye.
Legyen
![]() . Így
. Így

Mivel
![]() ,
, ![]() .
.
Ezt
(1) -be helyettesítve:
![]()
![]()
Így
![]()
![]()
![]() .
.
Röviden
írva
![]()
![]() .
.
Ez
az összefüggés az ![]() és
és ![]() koordinátarendszerek
közötti transzformációs formula. Az inverz reláció hasonlóan adódik:
koordinátarendszerek
közötti transzformációs formula. Az inverz reláció hasonlóan adódik:
![]()
![]()
5. Definíció: Az M n-dimenziós topológikus sokaság egy ![]() koordinátakörnyezet
rendszerét Cr
osztályú koordinátakörnyezet rendszernek, vagy Cr
koordináta környezetnek nevezzük, ha S
a követkető tulajdonságokkal rendelkezik:
koordinátakörnyezet
rendszerét Cr
osztályú koordinátakörnyezet rendszernek, vagy Cr
koordináta környezetnek nevezzük, ha S
a követkető tulajdonságokkal rendelkezik:
Minden
![]() -ra,
melyre
-ra,
melyre ![]() nem üres halmaz, az
nem üres halmaz, az ![]() -változós
-változós
22. oldal
függvények,
amelyek az ![]() és
és ![]() koordináta környezetek
közötti transzformációval vannak meghatározva, a
koordináta környezetek
közötti transzformációval vannak meghatározva, a ![]() illetve a
illetve a ![]() halmazokon, r -szeresen folytonosan
differenciálhatók. Ha
halmazokon, r -szeresen folytonosan
differenciálhatók. Ha ![]() és
és ![]() mindegyike analitikus
függvény, akkor S -et
mindegyike analitikus
függvény, akkor S -et ![]() osztályú
koordinátakörnyezet rendszernek vagy
osztályú
koordinátakörnyezet rendszernek vagy ![]() koordinátakörnyezet
rendszernek nevezzük. Ha az S
egy Cr
osztályú koordinátakörnyezet rendszer,
koordinátakörnyezet
rendszernek nevezzük. Ha az S
egy Cr
osztályú koordinátakörnyezet rendszer, ![]() az M -en, akkor
azt mondjuk, hogy az S egy Cr
osztályú differenciálható struktúrát definiál az M topológikus sokaságon.
az M -en, akkor
azt mondjuk, hogy az S egy Cr
osztályú differenciálható struktúrát definiál az M topológikus sokaságon.
6. Definíció: Ha az M
egy topológikus sokaság az S Cr
osztályú koordinátakörnyezet rendszerrel, akkor M -et n-dimenziós Cr
osztályú differenciálható sokaságnak, vagy Cr sokaságnak
nevezzük. Nevezetesen, ha ![]() , akkor az M -et analitikus sokaságnak nevezzük.
, akkor az M -et analitikus sokaságnak nevezzük.
7. Definíció: Legyen az M
egy Cr
sokaság, D az M -nek egy nyílt halmaza és ![]() egy Cr
osztályú atlasz. Legyen
egy Cr
osztályú atlasz. Legyen ![]() , és legyen
, és legyen ![]() a
a ![]() -nak az
-nak az ![]() -ra való megszorítása. Ekkor
-ra való megszorítása. Ekkor ![]() a D -n egy Cr
atlasz, és D egy Cr sokaság. A D -t az M nyílt részsokaságának nevezzük.
a D -n egy Cr
atlasz, és D egy Cr sokaság. A D -t az M nyílt részsokaságának nevezzük.
23. oldal
1. Definíció: Legyen M
egy n-dimenziós
Cr
![]() sokaság. Legyen
sokaság. Legyen ![]() nyílt halmaz, és f ezen egy folytonos függvény. Legyen
nyílt halmaz, és f ezen egy folytonos függvény. Legyen ![]() az M egy Cr atlasza. Legyen
az M egy Cr atlasza. Legyen ![]() és V a p -nek egy olyan környezete, hogy
és V a p -nek egy olyan környezete, hogy ![]() igaz valamely
igaz valamely ![]() -ra.
Ha az En
egy
-ra.
Ha az En
egy ![]() nyílt részhalmazán
definiált
nyílt részhalmazán
definiált ![]()
![]() függvény Cs
függvény Cs ![]() osztályú a
osztályú a ![]() egy környezetében,
akkor azt mondjuk, hogy az f
a
egy környezetében,
akkor azt mondjuk, hogy az f
a ![]() -ban
Cs
osztályú.
-ban
Cs
osztályú.
2. Definíció: Ha az f
függvény az ![]() minden pontjában Cs
osztályú, akkor Cs
osztályúnak nevezzük az U
-n.
minden pontjában Cs
osztályú, akkor Cs
osztályúnak nevezzük az U
-n.
Tegyük
fel, hogy az f Cr osztályú az M -beli p pont egy környezetében. Ha ![]() , akkor
, akkor
![]()
alakú
a ![]() egy környezetében. Itt
az
egy környezetében. Itt
az ![]() az
az
![]() változóknak Cs
osztályú függvényei. Ha
változóknak Cs
osztályú függvényei. Ha ![]() és
és ![]() , akkor
, akkor
![]() .
.
Vagy
röviden ![]() .
.
24. oldal
Azt
kaptuk tehát, hogy
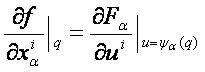
Tegyük
fel, hogy a p az ![]() -ban is benne van és legyen
-ban is benne van és legyen
![]()
a p pont egy környezetében és legyen ![]() minden
minden ![]() . Azt kapjuk, hogy
. Azt kapjuk, hogy
![]() .
.
Ennélfogva
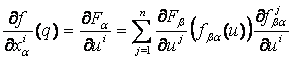
De
![]() ,
,
így
 ,
, 
Ezáltal
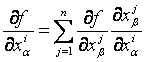
és
hasonlóan

igaz
minden ![]() -beli pontra.
-beli pontra.
Nevezetesen,
ha ![]() és
és ![]() , akkor
, akkor
 ,
, 
is
igaz minden ![]() -beli
pontra. Legyen
-beli
pontra. Legyen
25. oldal

Ekkor
![]() (egységmátrix).
(egységmátrix).
Így
az ![]() és
és ![]() egymás inverzei és így
egymás inverzei és így
![]() az
az ![]() egyetlen pontjában
sem.
egyetlen pontjában
sem.
3. Definíció: Legyenek az f1,
f2,…, fn függvények a p egy U környezetében definiált Cs osztályú függvények. ![]() esetén legyen
esetén legyen
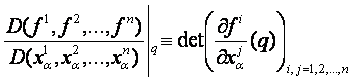 .
.
Ezt
az f1, f2,…, fn függvényeknek az ![]() lokális
koordinátarendszerre vonatkozó függvénydeterminánsának nevezzük.
lokális
koordinátarendszerre vonatkozó függvénydeterminánsának nevezzük.
Ha
![]() , akkor az előzőek alapján:
, akkor az előzőek alapján:
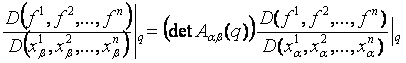
Így
a
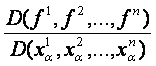
függvénydeterminánsnak
azon tulajdonsága, hogy 0 -e vagy
nem, független a p -t tartalmazó ![]() megválasztásától.
megválasztásától.
4. Definíció: Legyen az M egy n-dimenziós Cr sokaság. Legyen f1, f2,…, fn n darab Cs ![]() osztályú függvény a
osztályú függvény a ![]() egy környezetében, s
erre teljesüljön, hogy
egy környezetében, s
erre teljesüljön, hogy
26. oldal
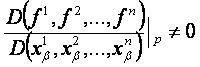
![]() .
.
Ekkor
az (f1, f2,…, fn) függvényennest
egy p körüli lokális
koordinátarendszernek nevezzük.
5. Definíció: Legyen M
egy n-dimenziós
Cr
sokaság ![]() és legyen
és legyen
![]() az M egy Cr osztályú atlasza.
Legyen
az M egy Cr osztályú atlasza.
Legyen ![]() az M -nek egy
olyan koordináta környezete, hogy az S
-ből az
az M -nek egy
olyan koordináta környezete, hogy az S
-ből az ![]() hozzá vételével nyert
atlasz Cs
osztályú
hozzá vételével nyert
atlasz Cs
osztályú ![]() , akkor azt mondjuk, hogy az
, akkor azt mondjuk, hogy az ![]() a Cr osztályú M sokaság Cs osztályú
koordináta környezete.
a Cr osztályú M sokaság Cs osztályú
koordináta környezete.
Tekintsük
a
![]()
Az
U n darab ![]() függvényét a Cr
osztályú M sokaság egy U halmazán értelmezett Cs
osztályú lokális koordinátarendszerének nevezzük.
függvényét a Cr
osztályú M sokaság egy U halmazán értelmezett Cs
osztályú lokális koordinátarendszerének nevezzük.
27. oldal
3. Differenciálható leképezések,
differenciálható görbék
Legyen M és
M’ n és m dimenziós
differenciálható sokaságok. A továbbiakban, ha mást nem mondunk, mindig ![]() osztályú sokaságokkal
foglalkozunk. Legyen
osztályú sokaságokkal
foglalkozunk. Legyen ![]() az M -nek M’ -re való folytonos leképezése.
Legyen
az M -nek M’ -re való folytonos leképezése.
Legyen ![]() és legyen f a
és legyen f a ![]() -nek az M’ -beli V koordinátakörnyezetén definiált
-nek az M’ -beli V koordinátakörnyezetén definiált ![]() osztályú függvénye.
Mivel
osztályú függvénye.
Mivel ![]() folytonos, így van a p -nek olyan U környezete, hogy
folytonos, így van a p -nek olyan U környezete, hogy ![]() . Definiáljuk a
. Definiáljuk a ![]() függvényt a p U
környezetén a következőképpen:
függvényt a p U
környezetén a következőképpen:
![]()
Mivel
f és ![]() folytonosak, a
folytonosak, a ![]() is folytonos. Ha
tetszőleges, a
is folytonos. Ha
tetszőleges, a ![]() környezetén definiált
környezetén definiált ![]() osztályú f függvényre a
osztályú f függvényre a ![]()
![]() osztályú a p egy környezetén, akkor azt mondjuk,
hogy a
osztályú a p egy környezetén, akkor azt mondjuk,
hogy a ![]()
![]() osztályú a p pontban vagy, hogy differenciálható.
osztályú a p pontban vagy, hogy differenciálható.
1. Definíció: Ha az M -nek M’ -re való
![]() differenciálható
leképezése egy-egyértelmű és a
differenciálható
leképezése egy-egyértelmű és a ![]() inverze is
differenciálható, akkor a
inverze is
differenciálható, akkor a ![]() -t az M -nek M’ -re való
diffeomorf leképezésének, vagy diffeomorfizmusának nevezzük.
-t az M -nek M’ -re való
diffeomorf leképezésének, vagy diffeomorfizmusának nevezzük.
2. Definíció: Legyen (a, b)
az R egy nyílt intervalluma. Az R egy 1-dimenziós differenciálható sokaság és (a, b) az R egy nyílt
részsokasága. Az (a, b) -nek egy M -be
28. oldal
való
![]() differenciálható
leképezését az M -nek
az (a, b) -n értelmezett differenciálható
görbéjének nevezzük.
differenciálható
leképezését az M -nek
az (a, b) -n értelmezett differenciálható
görbéjének nevezzük.
3. Definíció: Ha ![]() az [a, b] zárt intervallumnak egy M sokaságba való leképezése, és ha
létezik egy olyan (a’, b’) nyílt
intervallum, mely tartalmazza [a, b]
-t , valamint egy olyan
az [a, b] zárt intervallumnak egy M sokaságba való leképezése, és ha
létezik egy olyan (a’, b’) nyílt
intervallum, mely tartalmazza [a, b]
-t , valamint egy olyan ![]() differenciálható
leképezés, hogy
differenciálható
leképezés, hogy ![]() , ha
, ha ![]() , akkor
, akkor ![]() -t az M -nek az [a, b] -n
definiált differenciálható görbéjének nevezzük.
-t az M -nek az [a, b] -n
definiált differenciálható görbéjének nevezzük.
4. Definíció: Ha ![]() egy olyan folytonos
leképezés, hogy az [a, b] véges
számú a0, a1,…, am pontjaira a=a0<a1<a2<…<am=b és a
egy olyan folytonos
leképezés, hogy az [a, b] véges
számú a0, a1,…, am pontjaira a=a0<a1<a2<…<am=b és a ![]() -nek az [a0, a1],
[a1, a2],…, [am-1, am]
-re való szűkítései differenciálható görbék, akkor
-nek az [a0, a1],
[a1, a2],…, [am-1, am]
-re való szűkítései differenciálható görbék, akkor ![]() -t szakaszonként differenciálható görbének nevezzük.
-t szakaszonként differenciálható görbének nevezzük.
5. Definíció: Legyen a ![]() az M
differenciálható sokaságnak az (a, b)
-n definiált differenciálható görbéje. Legyen
az M
differenciálható sokaságnak az (a, b)
-n definiált differenciálható görbéje. Legyen ![]() és (x1, x2,…, xn) az M
-nek egy lokális koordinátarendszere a
és (x1, x2,…, xn) az M
-nek egy lokális koordinátarendszere a ![]() egy környezetében és
legyen
egy környezetében és
legyen
![]() (i = 1, 2,…, n).
(i = 1, 2,…, n).
Minden
![]() a t0 egy környezetének
a t0 egy környezetének ![]() osztályú függvénye. Az
osztályú függvénye. Az
29. oldal

n-dimenziós
vektort a ![]() görbe
görbe ![]() pontjában az (x1, x2,…, xn) lokális koordinátarendszerre
vonatkoztatott érintővektorának nevezzük.
pontjában az (x1, x2,…, xn) lokális koordinátarendszerre
vonatkoztatott érintővektorának nevezzük.
30. oldal
III. Érintővektorterek
Ebben a fejezetben megkonstruáljuk a bevezetésben
tárgyalt érintőtér általánosításaként a sokaság érintőterét. Az érintőtér
alapvető szerepet játszik a Riemann metrika
értelmezésében.
Majd tekintjük a sokaság érintő nyalábját, mint a
pontbeli érintőtelek unióját. Ezt természetes módon differenciálható
struktúrával látjuk el. Ez a konstrukció a modern differenciálható sokaságok
elméletében igen jelentős. Említést teszünk a hasonló jelentőségű principális
nyalábról is.
31. oldal
1. Az érintővektor
Legyen M
egy sokaság és p az M -nek egy
pontja. Tekintsük mindazon ![]() osztályú függvények
halmazát, melyek a p egy
környezetében vannak definiálva. Jelöljük ezt a halmazt F(p) -vel. Nyilván, hogy ha f és
osztályú függvények
halmazát, melyek a p egy
környezetében vannak definiálva. Jelöljük ezt a halmazt F(p) -vel. Nyilván, hogy ha f és ![]() ,
, ![]() akkor
akkor ![]() . Ha minden
. Ha minden ![]() -nek megfelel egy olyan v(f) valós szám, amely kielégítik a
következő feltételeket:
-nek megfelel egy olyan v(f) valós szám, amely kielégítik a
következő feltételeket:
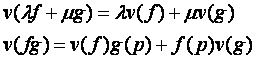
ahol
![]() , akkor a
, akkor a ![]() leképezést az M p
-beli érintővektorának nevezzük.
leképezést az M p
-beli érintővektorának nevezzük.
Megjegyezzük, hogy a v(f) értéke az f -nek csak a lokális viselkedésétől függ.
32. oldal
2. Az érintőtér
Az M -nek legyen v és
v’ a p -beli érintővektora és ![]() . Definiáljuk ezek összeadását illetve
. Definiáljuk ezek összeadását illetve ![]() -val való szorzását a
következőképpen:
-val való szorzását a
következőképpen:
![]()
Ekkor
a v+v’ és ![]() az M -nek p -beli
érintővektorai. Erre az összeadásra és skalárral való
szorzásra nézve a p -beli érintővektorok halmaza az R felett egy vektorteret alkot. Ezt a vektorteret Tp(M) -vel
jelöljük és az M p -beli érintőterének
nevezzük.
az M -nek p -beli
érintővektorai. Erre az összeadásra és skalárral való
szorzásra nézve a p -beli érintővektorok halmaza az R felett egy vektorteret alkot. Ezt a vektorteret Tp(M) -vel
jelöljük és az M p -beli érintőterének
nevezzük.
Legyen az (x1,
x2,…, xn) az U egy lokális koordinátarendszere és egy
![]() -ban legyen:
-ban legyen:
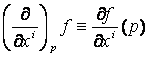 , (i = 1, 2,…, n)
, (i = 1, 2,…, n)
Ekkor
a ![]() egy p -beli
érintővektor.
egy p -beli
érintővektor.
Tétel: Ha az M
egy n-dimenziós
differenciálható sokaság, akkor a Tp(M)
érintőtere szintén n-dimenziós
és  ennek egy bázisa.
ennek egy bázisa.
Legyen ![]() és legyen
és legyen ![]() . A
. A ![]() számennest
a v -nek
az (x1, x2,…, xn) lokális koordinátarendszerre vonatkozó komponenseinek
nevezzük. Ekkor
számennest
a v -nek
az (x1, x2,…, xn) lokális koordinátarendszerre vonatkozó komponenseinek
nevezzük. Ekkor
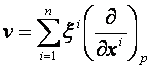
Legyen
(x1, x2,…, xn) és ![]() a p pont két lokális koordinátarendszere. Ekkor
a p pont két lokális koordinátarendszere. Ekkor 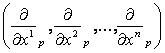 és a
és a  a Tp(M) -nek egy egy bázisa és a köztük lévő transzformációs
a Tp(M) -nek egy egy bázisa és a köztük lévő transzformációs
33. oldal
törvény:
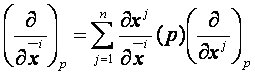
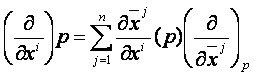
Ha ![]() és
és ![]() az
az ![]() -re vonatkozó komponensei, akkor
ezek transzformációs törvénye:
-re vonatkozó komponensei, akkor
ezek transzformációs törvénye:

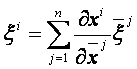
Legyen most a ![]() az M -nek egy (a, b) -n definiált differenciálható
görbéje és
az M -nek egy (a, b) -n definiált differenciálható
görbéje és ![]() . Legyen (x1,
x2,…, xn) az M egy lokális koordinátarendszere és
legyen
. Legyen (x1,
x2,…, xn) az M egy lokális koordinátarendszere és
legyen 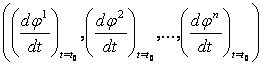 a
a ![]() görbe
görbe ![]() -beli érintővektora az (x1, x2,…, xn) lokális koordinátarendszerben. Legyen
-beli érintővektora az (x1, x2,…, xn) lokális koordinátarendszerben. Legyen
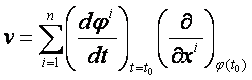
Ekkor
a v az M -nek egy érintővektora a ![]() pontban és ez
független az (x1, x2,…,
xn) lokális koordinátarendszer
megválasztásától. – Valóban, ha
pontban és ez
független az (x1, x2,…,
xn) lokális koordinátarendszer
megválasztásától. – Valóban, ha ![]() egy másik
egy másik ![]() -hoz tartozó lokális koordinátarendszer és ha
-hoz tartozó lokális koordinátarendszer és ha ![]() , akkor
, akkor

A v -t a ![]() differenciálható
görbe
differenciálható
görbe ![]() -beli érintővektorának
nevezzük.
-beli érintővektorának
nevezzük.
34. oldal
Ha a ![]() differenciálható görbe
érintővektora egyetlen pontban sem zérus, és ha
differenciálható görbe
érintővektora egyetlen pontban sem zérus, és ha ![]() ha
ha ![]() , akkor a
, akkor a ![]() -t reguláris differenciálható görbének nevezzük.
-t reguláris differenciálható görbének nevezzük.
35. oldal
3. Vektormezők, derivációk
Az M minden
pontjában tekintsünk egy Xp -vel jelölt
érintővektort. Az ![]() megfeleltetést az M -en egy vektormezőnek
nevezzük.
megfeleltetést az M -en egy vektormezőnek
nevezzük.
Ha az (x1,
x2,…, xn) az M egy U nyílt halmazának lokális koordinátarendszere, akkor az U minden p pontjában az Xp egyértelműen felírható
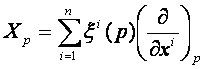
alakban.
Ebben az esetben a ![]() (i = 1, 2,…, n) az U -n n darabfüggvény, melyet az X vektormezőnek az (x1, x2,…, xn)
lokális koordinátarendszerre vonatkoztatott komponenseinek nevezzük. Ha
az
(i = 1, 2,…, n) az U -n n darabfüggvény, melyet az X vektormezőnek az (x1, x2,…, xn)
lokális koordinátarendszerre vonatkoztatott komponenseinek nevezzük. Ha
az ![]() az
U egy másik lokális
koordinátarendszere és
az
U egy másik lokális
koordinátarendszere és ![]() az X -nek az
az X -nek az ![]() -ra vonatkoztatott komponensei,
akkor
-ra vonatkoztatott komponensei,
akkor
 ahol
ahol ![]() .
.
Így
az X komponens függvényeinek az a
tulajdonsága, hogy egy pontban folytonos vagy Cr osztályú,
független a koordinátarendszer megválasztásától. Így ha az X -nek az összes komponens függvénye
folytonos vagy Cr
osztályú, akkor az X -et folytonos vagy Cr osztályú
vektromezőnek nevezzük az U
-n.
Ha az M
minden pontjának létezik olyan környezete, melyen az X folytonos vagy Cr osztályú, akkor azt mondjuk, hogy az X az M folytonos vagy Cr osztályú vektormezője.
36. oldal
Jelöljük az M
összes ![]() osztályú
vektormezőinek halmazát
osztályú
vektormezőinek halmazát ![]() -mel, és
-mel, és ![]() -en definiált összes
-en definiált összes ![]() osztályú függvények
halmazát. Legyen
osztályú függvények
halmazát. Legyen ![]() és
és ![]() . A
. A

megfeleltetések
az M -nek
vektormezői. Ezekre a következő szabályok érvényesek:
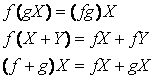
Most
ha (x1, x2,…, xn) az U
-nak egy lokális koordinátarendszere, akkor legyen:
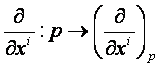
Egy
vektormezőnek az (x1, x2,…,
xn) -re vonatkozó komponensei az U -nak ![]() osztályú függvényei,
ha az X is
osztályú függvényei,
ha az X is ![]() osztályú, és X az U -n így írható fel:
osztályú, és X az U -n így írható fel:
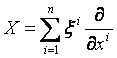
Legyen
![]() és
és ![]() . Definiáljunk M -en egy Xf -el jelölt függvényt az
. Definiáljunk M -en egy Xf -el jelölt függvényt az
![]()
![]()
előírással.
Így
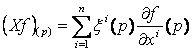
és
Xf ![]() osztályú. Az Xf -et az f
-nek az X
vektormezőre vonatkozó deriváltjának nevezzük. Az X által definiált derivációra a következő
szabályok érvényesek:
osztályú. Az Xf -et az f
-nek az X
vektormezőre vonatkozó deriváltjának nevezzük. Az X által definiált derivációra a következő
szabályok érvényesek:

37. oldal
Most
az algebrák definiálására térünk át.
1. Definíció: Legyen V
az R felett egy vektortér. Ha a V minden a, b elem-párjához van a V
-nek egy ![]() -vel jelölt eleme és teljesülnek a
-vel jelölt eleme és teljesülnek a
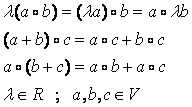
relációk,
akkor a V -t R feletti algebrának nevezzük.
2. Definíció: Ha az R
feletti V algebrában az
![]()
reláció
is teljesül, akkor V -t asszociatív
algebrának nevezzük.
3. Definíció: Legyen V
egy R feletti algebra. Ha D a V -nek olyan önmagára való leképezése,
melyre teljesülnek a következő feltételek:

akkor
a D -t a V algebra egy derivációjának
nevezzük.
4. Definíció: Legyen V
egy asszociatív algebra az R felett
és legyen W egy vektortér szintén az
R felett.
38. oldal
Ha
megadható egy olyan
![]()
művelet,
melyre teljesülnek a következő:

relációk,
akkor a W -t V -modulusnak nevezzük.
5. Definíció: Legyen D1,
D2 egy algebra két derivációja. Definiáljuk a V -nek egy [D1, D2] -vel
jelölt önmagára való lineáris leképezését a következőképpen:
[D1, D2]a = D1(D2a)
– D2(D1a).
A [D1, D2] -t a V D1, D2 derivációi kommutátorszorzatának
nevezzük.
1. Tétel: Egy V
algebra két derivációjának kommutátorszorzata
a V -nek
ismét derivációja.
2. Tétel: A derivációk kommutátorszorzata rendelkezik a következő
tulajdonságokkal:
[D1, D2] = -[D2,
D1]
[D1, [D2, D3]]
+ [D2, [D3, D1]] + [D3, [D1,
D2]] = 0
Ez
utóbbit a kommutátorszorzás Jacobi
azonosságának is szokták nevezni.
6. Definíció: Legyen V az
R felett egy algebra. Ha a V a, b elem-párjaira értelmezett ![]() -vel jelölt művelete eleget tesz az
-vel jelölt művelete eleget tesz az
39. oldal
[a, b] = -[b, a]
[a, [b, c]] + [b, [c, a]] + [c, [a, b]]
= 0
feltételeknek
is, akkor a V -t R feletti Lie
algebrának, az algebra műveletét pedig kommutátor szorzásnak
nevezzük.
Ha
a függvények összeadását és szorzását a szokásos módon definiáljuk, akkor ![]() egy asszociatív
algebra. Ha
egy asszociatív
algebra. Ha ![]() és
és ![]() , akkor
, akkor ![]() . Erre a szorzásra nézve a
. Erre a szorzásra nézve a ![]()
![]() -modulus. Legyen továbbá
-modulus. Legyen továbbá
![]()
Ekkor
a DX a ![]() asszociatív algebrának
egy derivációja. Kimondunk egy olyan tételt, mely azt
fejezi ki, hogy a
asszociatív algebrának
egy derivációja. Kimondunk egy olyan tételt, mely azt
fejezi ki, hogy a ![]() minden derivációja DX
alakú.
minden derivációja DX
alakú.
3. Tétel: Ha az M
két X és Y vektormezőjére DX
= DY igaz, akkor X
ekvivalens Y -nal.
4. Tétel: Ha a D a ![]() asszociatív algebra
egy derivációja, akkor létezik az M -nek egy
egyértelműen meghatározott X
vektormezője úgy, hogy D = DX.
asszociatív algebra
egy derivációja, akkor létezik az M -nek egy
egyértelműen meghatározott X
vektormezője úgy, hogy D = DX.
Tekintsük
a ![]() két DX és DY derivációját és ezek kommutátorszorzata legyer [DX, DY]. Ez a
két DX és DY derivációját és ezek kommutátorszorzata legyer [DX, DY]. Ez a ![]() -nek ismét egy derivációja,
így létezik olyan
-nek ismét egy derivációja,
így létezik olyan ![]() , hogy [DX,
DY] = DZ. Ezt Z vektormezőt az X és Y vektormezők kommutátorszorzatának nevezzük és Z = [X, Y] -nal
jelöljük, azaz
, hogy [DX,
DY] = DZ. Ezt Z vektormezőt az X és Y vektormezők kommutátorszorzatának nevezzük és Z = [X, Y] -nal
jelöljük, azaz
[DX, DY] = D[X, Y].
40. oldal
Így
minden ![]() esetén
esetén
[X, Y]f = X(Yf)
- Y(Xf)
A
vektormezők kommutátor szorzata rendelkezik a következő tulajdonságokkal:
[X+Y, Z] = [X, Z] + [Y, Z]
[X, Y+Z] = [X, Y] + [X, Z]
[X, Y] = -[Y, Z]
[fX, gY] = fg[X, Y] + f(Xg)Y - g(Yf)X
![]()
[X, [Y, Z]] + [Y, [Z, X]] + [Z, [X, Y]]
= 0
Legyen
az X és Y -nak az (x1, x2,…, xn)
-re vonatkozó komponensei ![]() és
és ![]() . Ekkor
. Ekkor
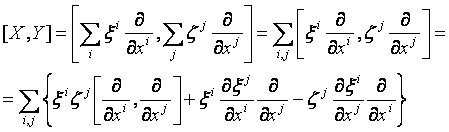
Mivel

azt
mondjuk, hogy
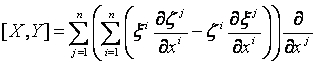
az
U -n.
5. Tétel: A ![]() halmaz a vektormezők kommutátorszorzására nézve Lie
algebrát alkot, és ez a Lie algebra azonosítható a
halmaz a vektormezők kommutátorszorzására nézve Lie
algebrát alkot, és ez a Lie algebra azonosítható a ![]() asszociatív algebra derivációinak Lie algebrájával.
asszociatív algebra derivációinak Lie algebrájával.
41. oldal
4. Az érintő nyaláb
Legyen M
egy differenciálható sokaság.
Legyen
![]()
Tegyük
![]() -et differenciálható sokasággá a
következőképpen:
-et differenciálható sokasággá a
következőképpen:
Ha ![]() , akkor legyen az
, akkor legyen az ![]() az M -nek olyan
lokális környezete, hogy
az M -nek olyan
lokális környezete, hogy ![]() és legyen (x1, x2,…, xn) az
és legyen (x1, x2,…, xn) az ![]() -nak lokális koordinátarendszere.
-nak lokális koordinátarendszere.
Legyen
![]()
egy
leképezés. Ekkor
![]()
![]() -ben legyenek a nyílt halmazok
definíció szerűen a
-ben legyenek a nyílt halmazok
definíció szerűen a ![]() -k, miközben az U
befutja az M koordináta
környezeteit. Az ezen nyílt halmazok által megadott topológiára nézve a
-k, miközben az U
befutja az M koordináta
környezeteit. Az ezen nyílt halmazok által megadott topológiára nézve a ![]() – ismeretes módon –
folytonos.
– ismeretes módon –
folytonos.
Ha ![]() , akkor
, akkor
![]()
és
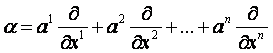
A
![]()
leképezés
egy-egyértelmű a ![]() és az E2n egy nyílt részhalmaza
között. A
és az E2n egy nyílt részhalmaza
között. A ![]() -nek az előzőekben definiált
topológiájára nézve a
-nek az előzőekben definiált
topológiájára nézve a ![]() leképezések homeomorfizmusok, miközben az U befutja az M összes
koordinátakörnyezetét.
leképezések homeomorfizmusok, miközben az U befutja az M összes
koordinátakörnyezetét.
42. oldal
Ezáltal a ![]() párok lokális
koordinátakörnyezeteknek tekinthetők. Vizsgáljuk meg ezen koordinátakörnyezetek
közötti kapcsolatot:
párok lokális
koordinátakörnyezeteknek tekinthetők. Vizsgáljuk meg ezen koordinátakörnyezetek
közötti kapcsolatot:
Legyen ![]() és
és ![]() az M két olyan lokális
koordinátakörnyezete, hogy
az M két olyan lokális
koordinátakörnyezete, hogy ![]() . Legyen
. Legyen ![]() az
az ![]() koordináta
transzformáció. Ekkor a
koordináta
transzformáció. Ekkor a ![]() differenciálható
leképezés. Ha
differenciálható
leképezés. Ha ![]() akkor
akkor
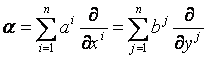
ahol
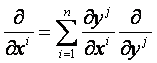 .
.
Így
![]() (j = 1, 2,…, n)
(j = 1, 2,…, n)
azaz
a b1, b2, …, bn koordináták az x1, x2, …, xn,
a1, a2, …, an
differenciálható függvényei. Így az (x1,
x2, …, xn, a1, a2,
…, an) -nak
az (y1, y2, …, yn, a1, a2, …, an) -re való transzformációja
differenciálható.
Ezáltal a ![]() -en differenciálható struktúrát
adtunk meg. A
-en differenciálható struktúrát
adtunk meg. A ![]() tehát 2n dimenziós differenciálható sokaság.
Ezt a
tehát 2n dimenziós differenciálható sokaság.
Ezt a ![]() sokaságot az M sokaság érintőnyalábjának
nevezzük.
sokaságot az M sokaság érintőnyalábjának
nevezzük.
43. oldal
Legyen M egy differenciálható sokaság.
Legyen:
![]()
Tegyük
B(M) -et
differenciálható sokasággá a következőképpen:
Ha ![]() , akkor legyen az
, akkor legyen az ![]() az
M -nek
olyan lokális koordinátakörnyezete, hogy
az
M -nek
olyan lokális koordinátakörnyezete, hogy ![]() és legyen az (x) az
és legyen az (x) az ![]() -nak lokális koordinátarendszere.
-nak lokális koordinátarendszere.
Legyen
![]()
egy
leképezés. Ekkor
![]()
A
![]()
leképezés
egy-egyértelmű a ![]() és az
és az ![]() egy nyílt halmaza között, ahol
egy nyílt halmaza között, ahol
![]()
és
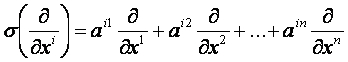
![]()
Belátható,
hogy a B(M) -nek
létezik egyértelműen egy olyan topológiája, hogy a ![]() leképezések homeomorfizmusok, miközben az U befutja az M összes
koordinátakörnyezetét.
leképezések homeomorfizmusok, miközben az U befutja az M összes
koordinátakörnyezetét.
Ezáltal
a ![]() párok lokális
koordinátakörnyezeteknek tekinthetők. Vizsgáljuk meg ezen koordinátakörnyezetek
párok lokális
koordinátakörnyezeteknek tekinthetők. Vizsgáljuk meg ezen koordinátakörnyezetek
44. oldal
közötti
kapcsolatot.
Legyen ![]() és
és ![]() az M két olyan lokális
koordinátakörnyezete, hogy
az M két olyan lokális
koordinátakörnyezete, hogy ![]() . Legyen (xi) és (yi) ezek lokális koordinátarendszerei.
Legyen
. Legyen (xi) és (yi) ezek lokális koordinátarendszerei.
Legyen ![]() az
az ![]() koordináta
transzformáció. Ekkor
koordináta
transzformáció. Ekkor ![]() differenciálható
leképezés. Ha
differenciálható
leképezés. Ha ![]() , akkor
, akkor
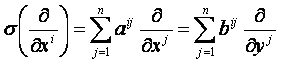
ahol
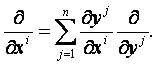
Ebből
azt kapjuk, hogy
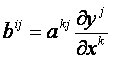
azaz
a bij
koordináták az x1, x2,
…, xn, a11, …, ann differenciálható függvényei.
Így
az (x1, x2, …, xn, a11, …, ann)
-nek az (y1,
y2, …, yn, b11, …, bnn) -re való transzformációja
differenciálható.
Így a B(M) -en differenciálható struktúrát adtunk meg. A B(M) tehát egy n+n2 dimenziós differenciálható sokaság. Ezt a B(M) sokaságot az M principális nyalábjának nevezzük.
45. oldal
IV. Riemann
sokaság
Ismeretes, hogy a Riemann
tér fogalma képezi a tulajdonképpeni modern differenciál geometria
kiindulópontját. Itt a korábbiakra támaszkodva egy olyan absztrakt értelmezését
adjuk, amely a Riemann geometria globális megközelítését
teszi lehetővé.
Hasonló szellemben adjuk meg a Finsler
sokaságok definícióját is, amely fogalomalkotás a modern differenciál
geometriai vizsgálatok egy másik kulcsfontosságú területének alapja.
46. oldal
Tegyük fel, hogy az M sokaság minden pontjában definiálva van egy ![]()
![]() pozitív belső szorzás.
Egy U -beli
(x1, x2,…, xn) koordinátarendszer esetén legyen
pozitív belső szorzás.
Egy U -beli
(x1, x2,…, xn) koordinátarendszer esetén legyen
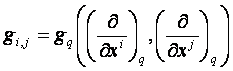
ahol
![]() . Minden gij (i, j
= 1, 2, …, n) az U egy függvénye
és a
. Minden gij (i, j
= 1, 2, …, n) az U egy függvénye
és a ![]() minden q -ra egy
pozitív definit szimmetrikus mátrix. Ha az
minden q -ra egy
pozitív definit szimmetrikus mátrix. Ha az ![]() az U -nak egy
másik koordinátarendszere, legyen
az U -nak egy
másik koordinátarendszere, legyen

Ekkor
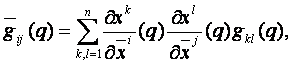
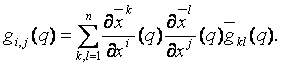
Így,
ha a gij
függvények az U -n Cr
osztályúak, akkor ![]() függvények is és
viszont, ezáltal ez a tulajdonság független a lokális koordinátarendszer
megválasztásától.
függvények is és
viszont, ezáltal ez a tulajdonság független a lokális koordinátarendszer
megválasztásától.
Ha
az M minden pontjának egy
környezetében az összes gij
függvény Cr
osztályú, akkor a Tp(M) -beli gp
pozitív belső szorzásával meghatározott ![]() leképezést, ahol p az M egy tetszőleges pontja, egy Cr osztályú
Riemann metrikának nevezzük. A gp -t
a g p -beli, a gij -t a g (x1,
x2,…, xn) -beli komponenseinek nevezzük. A továbbiakban csak
leképezést, ahol p az M egy tetszőleges pontja, egy Cr osztályú
Riemann metrikának nevezzük. A gp -t
a g p -beli, a gij -t a g (x1,
x2,…, xn) -beli komponenseinek nevezzük. A továbbiakban csak ![]() osztályú Riemann metrikákkal foglalkozunk, melyet egyszerűen Riemann metrikának nevezünk.
osztályú Riemann metrikákkal foglalkozunk, melyet egyszerűen Riemann metrikának nevezünk.
47. oldal
Ha adott az M
-en egy Riemann metrika,
akkor a p -beli
v érintővektor ![]() hosszát a
hosszát a
![]()
összefüggéssel
definiáljuk.
Ha
a v komponensei a (x1, x2,…,
xn) -ben ![]() , akkor
, akkor
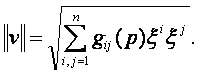
A Riemann metrikát gyakran a
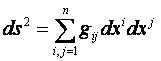
formulával
adják meg.
Egy olyan M
sokaságot, melyen egy g Riemann metrika adott, Riemann
sokaságnak nevezzük és (M, g) -vel jelöljük.
Legyen ![]() az (M, g) Riemann
sokaság egy (a, b) nyílt
intervallumon definiált differenciálható görbéje és vt ennek a
az (M, g) Riemann
sokaság egy (a, b) nyílt
intervallumon definiált differenciálható görbéje és vt ennek a ![]() -beli érintővektora. Ekkor a
-beli érintővektora. Ekkor a ![]() a t -nek folytonos függvénye. Ha a<c<d<b, akkor
a t -nek folytonos függvénye. Ha a<c<d<b, akkor
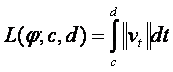
értéket
a ![]()
![]() és
és ![]() közötti hosszának
nevezzük.
közötti hosszának
nevezzük.
Egy
[a, b] zárt intervallumon definiált
differenciálható ![]() görbe esetén legyen
görbe esetén legyen ![]() az (a’, b’) nyílt halmazon (melyre:
az (a’, b’) nyílt halmazon (melyre: ![]() ) definiált differenciálható görbe úgy, hogy
) definiált differenciálható görbe úgy, hogy ![]() ha
ha ![]() . Legyen
. Legyen ![]() és nevezzük ezt a
és nevezzük ezt a ![]() görbe hosszának.
Ha a
görbe hosszának.
Ha a ![]() egy szakaszonként
differenciálható görbe, akkor ennek hossza egyenlő a
egy szakaszonként
differenciálható görbe, akkor ennek hossza egyenlő a
48.oldal
véges
számú zárt intervallumon adott differenciálható görbe hosszainak összegével.
Legyen
(M, g) egy Riemann
sokaság és ![]() . Legyen Cp,q
a p és q -t összekötő összes szakaszonként differenciálható görbék
halmaza. Ha
. Legyen Cp,q
a p és q -t összekötő összes szakaszonként differenciálható görbék
halmaza. Ha ![]() akkor
akkor ![]() legyen a
legyen a ![]() -nek a p és q közötti hossza.
Ha
-nek a p és q közötti hossza.
Ha
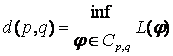
akkor
a d az M -en egy metrika. Ez a d metrika az M -en ugyanazt a topológiát indukálja,
mint amilyen az M -nek eredetileg volt.
49. oldal
Legyen M
egy n-dimenziós
differenciálható sokaság. Finsler sokaságon
értjük az (M, L) párt, ha
![]()
![]()
egy
függvény, mely a következő tulajdonságokkal rendelkezik:
![]() ahol:
ahol:![]()
![]()
![]() és
és ![]()
Az (M, L) Finsler sokaság metrikáját pozitív definit
Finsler metrikának nevezzük, ha a
![]()
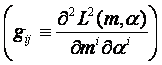
mátrix
pozitív definit.
50. oldal
Felhasznált irodalom:
Gacsályi Sándor: Topológia (Egyetemi jegyzet)
Yozo Matsushima: Differentiable Manifolds
L.Auslander – R.E.Mackenzie: Introduction to Differentiable Manifolds
Jelen
dolgozat az eredetinek – minden részletében vele megegyező – replikája.
(Készült:
2019. február)