Logika

A matematika fejlődése során szükségessé vált számos fontos - definíciókkal, axiómarendszerekkel, bizonyításokkal, algoritmusokkal stb. kapcsolatos - kérdésnek, a matematika alapjainak tisztázása. E célra igen hatásos eszköznek bizonyult a matematikai logika, amely a logikus gondolkodás formális tulajdonságait matematikai módszerekkel tárgyalja. A matematikai logika segítségével feltárt törvények és összefüggések elsősorban a matematika ítéletalkotási, következtetési és bizonyítási módszerei vonatkoznak. Ítéletek, adott ítéletekből való származtatásai, azaz a szillogizmusok helyessége szabatosan vizsgálható a matematikai logika egyik legfontosabb módszere, az ítéletekre vonatkozó Boole-algebra, az úgynevezett ítéletkalkulus segítségével.

Ítéletkalkulus

Az ítéletkalkulus a matematikai logikának az a fejezete, amely az úgynevezett logikai műveletekkel foglalkozik. A logikai művelet olyan művelet, amely a logikai ítéleteken van értelmezve, s a kapott logikai ítélet értéke csak azon ítéletek logikai értékétől függ, amelyekre a műveletet alkalmaztuk.

Ítélet (vagy állítás)

Az ítélet a matematikai logikának olyan alapfogalma, mint például a halmazelméletnek a halmaz, azaz nem definiáljuk. Elmondhatjuk azonban, hogy általában, minden ítélet megfelel egy olyan értelmes kijelentő magyar (természetesen azt minden nemzet mondhatja, hogy a saját nyelvét használja a leíráshoz) mondatnak, melynek állításáról egyértelműen el tudjuk dönteni, hogy igaz-e vagy hamis. Igaz továbbá, hogy egy ítéletnek csak két logikai értéke lehet: igaz (i) vagy hamis (h), harmadik lehetőség nincs.

Példák ítéletekre:

Három nagyobb, mint négy.

Ma április elseje van.

Most süt a nap.

Én járkálok.

Én magyarázok.

Pisti hazudik.

Nem ítéletek a következők:

Petőfi Sándor: A Tisza. (Nincs benne állítmány.)

Ez a ház nagy. (Az állítás relatív dolgot fejez ki.)

Jaj! (Nem kijelentő mondat.)

1848. május 12-én, Budapesten nem esett az eső. (Ellenőrizhetetlen.)

Én most hazudok. (Ellentmondásra vezet bármelyik logikai érték.)

Egyetlen igazság van: az hogy nincs igazság. (Ez is ellentmondásra vezet.)

Logikai műveletek

Annak érdekében, hogy általánosan érvényes összefüggéseket írhassunk fel ítéletekkel kapcsolatban - az algebrában szokásos módhoz hasonlóan - az ítéleteket betűkkel fogjuk helyettesíteni, például:

a = Én járkálok.

b = Én magyarázok.

Aszerint, hogy a logikai műveletben hány változó van, megkülönböztethetünk egyváltozós, kétváltozós és többváltozós logikai műveleteket.

Egyváltozós logikai művelet

Egyetlen egyváltozós logikai művelet létezik: a tagadás. Egyszerű konkrét esetben az ítélet tagadását úgy valósíthatjuk meg, hogy tagadjuk a kijelentő mondat állítását, azaz az állítmány elé "nem" szócskát mondunk.

Én járkálok. Tagadása: Én nem járkálok.

A magyar nyelvtani szabályokat is figyelembe véve megállapíthatjuk, hogy ez nem mindig pontosan valósítható meg, például:

Most nem esik az eső. Tagadása: Most esik az eső.

A 2 a 3 és 4 között van. Tagadása: A 2 nincs a 3 és 4 között.

Mindig járható út a tagadásra az, hogy ha az állítás elé elhelyezzük a következő mondatrészt: Nem igaz, hogy … és utána mondjuk azt, amit tagadni szeretnénk.

Mivel egy állítás logikai értéke csak igaz vagy hamis lehet, a tagadás logikai műveleti táblája a következő:

A	tagadás	Nem A
	i	h
	h	i

A tagadás műveletet hívhatjuk negációnak is, a programnyelvek pedig, a NOT szócska segítségével írják le ezt a műveletet. Algebrai jele: a, olvasd: "nem a".

A tagadás a halmazelméleti komplementer képzésnek a megfelelője.

Kétváltozós logikai műveletek

A diszjunkció.

Legyenek "a" és "b" ítéletek. Ha e két ítéletet a "vagy" kötőszóval kapcsoljuk össze, akkor egy összetett állítást alkottunk. Úgy mondjuk, logikai műveletet hajtottunk végre azért, mert az összetett állítás logikai értéke csak a műveletben résztvevő ítéletek logikai értékétől függ, és nem függ az ítéletek tényleges tartalmától. Azt mondjuk, hogy a "vagy" logikai műveletet definiáljuk, ha rögzítjük minden lehetséges esetre az összetett állítás logikai értékét. Természetesen nem felejtkezünk meg arról, hogy a hétköznapi életben mikor tartunk igaznak egy olyan egyszerű ítéletekből összeállított kijelentést, melyeket a vagy kötőszó köt össze.

Az "a vagy b" összetett állítás pontosan akkor hamis, ha mindkét (a és b) állítás hamis, egyébként igaz. (Vagyis akkor igaz, ha legalább az egyik állítás igaz.)

Nézzük a műveleti tábláját:

A	B
	Vagy	h	i
	h	h	i
	i	i	i

A "vagy" logikai műveletet hívhatjuk diszjunkciónak is, a programnyelvek pedig, az OR szócska segítségével írják le ezt a műveletet. Algebrai jele: a b, olvasd: a vagy b.

A diszjunkció a halmazelméleti unióképzés és az elemi műveletekből az összeadásnak a megfelelője.

A konjunkció.

Legyenek "a" és "b" ítéletek. Ha e két ítéletet az "és" kötőszóval kötjük össze, akkor - a "vagy"-hoz hasonlóan - egy újabb logikai műveletet definiálhatunk, természetesen figyelembe véve, hogy a hétköznapi életben mikor tartunk igaznak egy olyan összetett állítást, melyek részeit az "és" köti össze.

Az "a és b" összetett állítás pontosan akkor igaz, ha mindkét (a és b) állítás igaz, egyébként hamis. (Vagyis akkor hamis, ha legalább az egyik hamis.)

Nézzük a műveleti tábláját:

A	B
	És	h	i
	h	h	h
	i	h	i

Az "és" logikai műveletet hívhatjuk konjunkciónak is, a programnyelvek pedig, az AND szócska segítségével írják le ezt a műveletet. Algebrai jele: a b, olvasd: a és b.

A konjunkció a halmazelméleti metszetképzés és az elemi műveletekből a szorzásnak a megfelelője.

Az implikáció.

Legyenek "a" és "b" ítéletek. Ha e két ítéletet a következőképpen kötjük össze: Ha "a" akkor "b". akkor egy újabb kétváltozós logikai műveletet definiálhatunk. Ahhoz, hogy a logikai tábláját megalkossuk, célszerű egy mindennapi példát elemezni. Tegyük fel, hogy a nagyapa a következőképpen biztatja unokáját:

Ha a tanév végén kitűnő leszel, akkor veszek neked egy biciklit.

Ha jól meggondoljuk, akkor ez az összetett állítás csak egyetlen esetben lehet hamis, mármint akkor, ha a gyermek kitűnő lesz, és a nagyapa mégsem veszi meg a megígért ajándékot. Ekkor nem teljesül az ígéret, az unoka akár még orrolhat is a nagyapjára. Minden más eset megengedett a hétköznapokban. Azaz, ha nem lesz kitűnő a gyerek, a nagypapa jogosan nem vesz biciklit, de az is megengedett, hogy a gyengébb eredmény ellenére mégis vesz, ettől az unoka nem lesz haragos, csak legfeljebb igyekszik megszolgálni a nagypapa jólelkűségét, vagy ami rosszabb, lám nem kell teljesítenem, a jutalom úgysem marad el..

Mindezek alapján a: Ha "a" akkor "b" összetett állítás hamis, ha az "a" igaz és a "b" hamis, minden más esetben igaz.

Nézzük a műveleti tábláját:

A	B
	Ha akkor	h	i
	h	i	i
	i	h	i

A "ha … akkor …" logikai műveletet "… -ból következik …" -nek is olvashatjuk. Algebrai jele: a b, olvasd: "a nyíl b", "ha a akkor b", "a-ból következik b".

Az ekvivalencia.

Nézzük meg újra a nagypapa és unoka esetét. Mi van akkor, ha nagypapa szigorúbb és ezt mondja:

Ha a tanév végén kitűnő leszel, akkor veszek neked egy biciklit, de ha nem leszel kitűnő, nem veszek neked biciklit.

Ebben az esetben már logikailag nem lesz igaz az összetett állítás akkor, ha a tanuló gyenge eredménye ellenére biciklit kap a nagyapjától, hiszen kijelentette, ha nem lesz kitűnő, akkor nem kap biciklit. Azt mondhatjuk, hogy a kitűnő eredmény és az ajándék vásárlása most ugyanazt jelenti, azaz e két állítás azonos, vagy ekvivalens. A nagyapa mondatát így is fogalmazhatta volna:

Akkor és csak akkor veszek neked biciklit, ha kitűnő leszel.

A matematikában is vannak ilyen állítások, például:

Ha egy háromszög derékszögű, akkor igaz rá a Pithagorasz tétel, és megfordítva, ha igaz rá a Pithagorasz tétel, akkor a háromszög derékszögű. Vagy rövidebben: Egy háromszög akkor és csak akkor derékszögű, ha igaz rá a Pithagorasz tétel.

Mindezek alapján az: "a akkor és csak is akkor, ha b" összetett állítás akkor igaz, ha "a" és "b" logikai értéke megegyezik, azaz két esetben: ha mindkettő igaz, vagy ha mindkettő hamis. (Vagyis, ha a logikai értékek különbözőek, akkor az összetett állítás hamis, egyébként igaz.)

Nézzük a műveleti tábláját:

A	B
	Akkor és csak akkor, ha	h	i
	h	i	h
	i	h	i

Az ekvivalencia algebrai jele: a b, olvasd: "a" ekvivalens "b", "a" oda-vissza nyíl "b".

Kizáró vagy, vagy röviden: avagy.

Legyen a következő két állítás:

a = Víz alatt úszok.

b = Könyvet olvasok.

Ha ezek után képezzük a következő összetett állítást: Vagy "a" vagy "b", akkor könnyű belátni, hogy ez két esetben lehet igaz, ha "a" igaz és "b" hamis, vagy "a" hamis és "b" igaz. Rövidebben fogalmazva, ha "a" és "b" logikai értékei különbözőek, mint ahogy azt a konkrét példánk is megköveteli. Az így definiált műveletet kizáró vagy -nak szokás nevezni.

Nézzük a műveleti tábláját:

A	B
	Avagy	h	i
	h	h	i
	i	i	h

A kizáró vagy logikai műveletet (mivel az ekvivalenciának a negáltja) hívhatjuk antivalenciának is. Algebrai jele: a ▼ b. Olvasd: "a háromszög b", vagy "vagy a, vagy b", vagy "a avagy b". A programozásban a kizáró vagy neve az XOR.

A kizáró vagy halmazelméleti megfelelője a szimmetrikus differencia.

Eddig megismerkedtünk a következő kétváltozós logikai műveletekkel:

Diszjunkció,

Konjunkció,

Implikáció,

Ekvivalencia és

Antivalencia.

Vajon hány kétváltozós logikai művelet létezik. Ennek kiderítése érdekében készítsünk el egy olyan táblázatot, amelyben elhelyezzük a felsorolt öt műveletet, és egészítsük ki úgy, hogy minden lehetséges esetet tartalmazzon. Ehhez azt kell meghatározni, hogy egy 2*2-es táblázatot i és h jelekkel hányféleképpen lehet kitölteni. Mivel mindegyik mezőbe a többitől függetlenül írhatunk i vagy h jelet, ezért a lehetséges esetek száma 2*2*2*2, azaz 16.

A kész táblázat így néz ki:

B:

1.

2.

3.

4.

5.

6.

7.

8.

h

i

h

i

h

i

h

i

h

i

h

i

h

i

h

i

A:

h

h

h

i

h

h

i

h

h

h

h

i

i

i

h

i

h

i

h

h

h

h

h

h

h

i

i

h

h

h

h

i

i

h

H

Mindig Hamis

Sem-sem

És

Negáció

Ekviva-lencia

Negáció

B:

9.

10.

11.

12.

13.

14.

15.

16.

h

i

h

i

h

i

h

i

h

i

h

i

h

i

h

i

A:

h

h

i

h

i

h

h

i

i

i

i

i

h

h

i

i

i

i

h

i

i

h

i

i

h

i

i

h

i

i

i

i

i

i

B

a▼b

A

I

Avagy

Implikáció

Seffer vonal

Implikáció

Vagy

Mindig Igaz

Mivel a 16 rész egymás mellett nem fért el, ezért kétszer nyolcas táblát készítettünk. Az egyes táblázatrészek meg vannak sorszámozva 1-től 16-ig. A kitöltés menete: először minden mezőbe h került, aztán az egy i-t tartalmazó táblázatok következtek a 2.-tól 5.-ig. A 6.-tól 11.-ig két igen, a 12.-től 15.-ig 3 igen szerepel, majd a 16.-ban mindenütt igen.

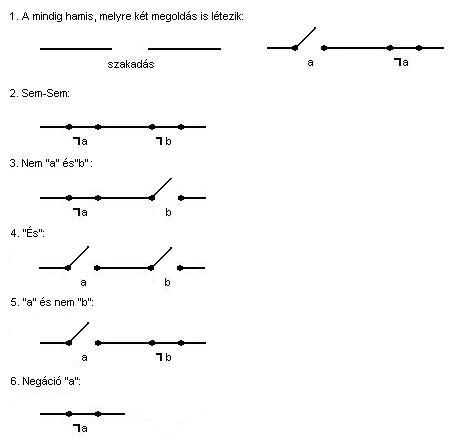
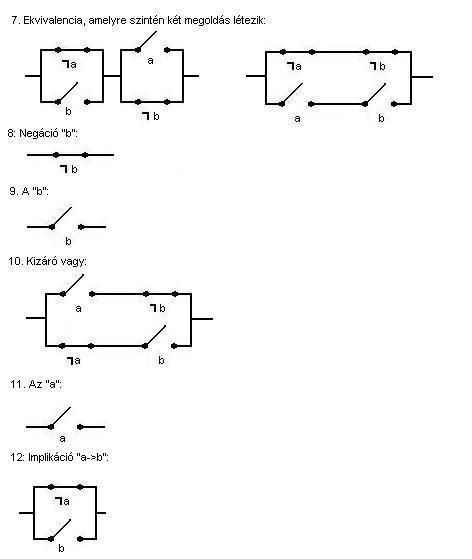
Könnyen beazonosíthatjuk a következő sorszámú táblákat:

1.: Azonosan hamis.

16.: Azonosan igaz.

15.: a b.

4.: a b.

12.: a b.

14.: b a.

7.: a b.

10.: a ▼ b.

További négy még - mint egyváltozós logikai művelet - felismerhető:

11.: a.

9.: b.

6.: a.

8.: b.

A maradék négy viszont ismeretlen:

2.: , a "vagy" művelet tagadása: Sem-Sem.

13.: , az "és" művelet tagadása: Seffer vonal, vagy NAND.

3.: , amelynek nincs külön elnevezése.

5.: , amelynek szintén nincs külön neve.

Ezzel mind a 16 táblát beazonosítottuk, azaz több kétváltozós logikai művelet nem létezhet.

Mivel a kettőnél több változót tartalmazó logikai műveletek mindegyike felírható a legfeljebb kétváltozós műveletekkel, ezért többváltozós logikai műveletekkel nem foglalkozunk.

A logikai műveletek tulajdonságai

Negáció.

a = a, azaz tagadás tagadása az eredeti állítással ekvivalens.

Diszjunkció.

, azaz a művelet szimmetrikus, amelyet úgy is felismerhetünk, hogy a műveleti táblán megrajzoljuk a bal-felső - jobb-alsó átlót, és megvizsgáljuk, hogy erre vonatkozóan a táblázat értékei szimmetriát mutatnak-e vagy sem, ha igen - mint esetünkben - akkor a művelet szimmetrikus.

, azaz a művelet asszociatív.

Konjunkció.

, azaz a művelet szimmetrikus.

, azaz a művelet asszociatív.

Implikáció.

, azaz a művelet nem szimmetrikus.

, azaz a művelet nem asszociatív.

Ekvivalencia.

, azaz a művelet szimmetrikus.

, azaz a művelet asszociatív.

Antivalencia.

a ▼ b = b ▼a, azaz a művelet szimmetrikus.

a ▼(b ▼c) = (a ▼b) ▼c, azaz a művelet asszociatív.

A de Morgan azonosság.

Nagyon hasznos azonosság, amely megmutatja, hogyan bontható fel a zárójelbe tett diszjunkció és konjunkcó, ha a zárójel előtt a negáció jele áll.

, azaz a felbontáskor a zárójelben lévő diszjunkcióból konjunkció lesz, és a zárójelben lévő állítások negáltját kell venni.

Hasonlóan:

, azaz a felbontáskor a zárójelben lévő konjunkcióból diszjunkció lesz, és a zárójelben lévő állítások negáltját kell venni.

Az ítéletkalkulus további fontos azonosságai.

Tétel: minden két vagy többváltozós logikai művelet felírható csak a negáció, a diszjunkció és a konjunkció, valamint zárójelek segítségével. (Ezt az állítást nem bizonyítjuk, csak több példával bemutatjuk.)

Az implikáció kifejezése a három alapművelettel:

. Ennek belátása végett keressük ki a 16 tábla közül a a és a b táblákat. Ezek: a 6. és a 9. táblák. Gondolatban helyezzük őket egymás felé és hajtsuk végre köztük egy "vagy" műveletet. Eredményül a 12-es táblát kapjuk, ami nem más, mint az implikáció. Hasonlóan: .

Az ekvivalencia kifejezése a három alapművelettel:

.

Az antivalencia kifejezése a három alapművelettel:

a ▼ b =

.

A disztributív tulajdonság.

Az elemi algebrában a szorzás az összeadásra nézve disztributív, azaz a*(b+c) = a*b+a*c, azaz a zárójel felbontható, az összeget tagonként kell megszorozni. Ez fordítva nem áll fent, azaz a+b*c (a+b)*(a+c). Nézzük milyen ezzel analóg azonosságok érvényesek a matematikai logikában.

, valamint

.

Ez utóbbi, figyelembe véve azt, hogy a logikai műveleteknek milyen algebrai műveletet feleltettünk meg, az elemi algebra átírásának tekinthető. Az előbbi disztributív törvénynek viszont nincs elemi algebrai megfelelője, mint ahogy azt fentebb le is írtuk.

A matematikai logika legfontosabb azonosságai.

A következő táblázatban felsoroltuk a legfontosabb azonosságokat a három alapművelettel kapcsolatban. Megjegyezzük, hogy a táblázat két oldala egymásnak úgynevezett duálisa. A dualitás a következőkben nyilvánul meg: ha egy logikai azonosság igaz, akkor igaz is marad, ha a benne szereplő jeleket a duális párjukkal helyettesítjük.

Duális párok:

és , (és viszont)

I és H, (és viszont)

és . (azaz a negáció duálisa önmaga).

a a = a	a a = a
a I = I	a H = H
a H = a	a I = a
a b = b a	a b = b a
(a b) c = a (b c)	(a b) c = a (b c)
a (b c) = (a b) (a c)	a (b c) = (a b) (a c)
a (a b) = a	a (a b) = a
I = H	H = I
a a = I	a a = H
a (b b) = a	a(b b) = a
(a b) = a b	(a b) = a b
a = a

A felsorolt 23 azonosság természetesen nem független, hiszen vannak olyanok, amelyeket az összes többi segítségével be lehet bizonyítani.

Példaként nézzük meg, hogy a jobb oldali oszlop de Morgan azonosságát hogyan bizonyíthatjuk a többi azonosság segítségével.

Írjuk fel a baloldali de Morgan azonosságot és helyettesítsünk bele "a" és "b" helyett a negáltjukat:

(a b) = a b = a b.

Most vegyük az első és utolsó oldal negáltját:

(a b) = ( a b).

Azaz:

( a b) = a b, azaz a jobboldali de Morgan azonosságot bebizonyítottuk.

A Boole algebra axiómái.

Már eddigiekben is többször tettünk említést arról, hogy a logikai műveletek sok rokonságot mutatnak a halmazalgebra műveleteivel, pontosabban a hatványhalmaz algebrával. (Hatványhalmaz: egy halmaz összes részhalmazainak halmaza. Ez a halmaz zárt a halmazműveletekre nézve, van egy minimális eleme, az üres halmaz, és egy maximális a teljes halmaz.)

Ha ügyesen választunk ki olyan azonosságokat, amelyek egymástól függetlenek, azaz bármelyikük igaz volta a többiből nem következik, valamint arra is ügyelünk, hogy minden azonosság a kiválasztottak segítségével bizonyítható, akkor egy axiómarendszerhez juthatunk.

Ismerkedjünk most meg ezzel az axiómarendszerrel.

1. a a = a.

2. a b = b a. (kommutativitás)

3. (a b) c = a (b c). (asszociativitás)

4. a (b c) = (a b) (a c). (disztributivitás)

5. a (b b) = a.

6. (a b) = a b. (de Morgan azonosság)

7. a = a. (tagadás tagadásának elve)

8. a a = I. (harmadik kizárt elve)

9. I = H.

Feladatok.

1. Igazoljuk a következő azonosságokat:

- p q = p q.

- q p = p q.

- p (p q) = p q.

- p (p q) = p q.

- p q = (p q) (p q).

2. Vizsgáljuk meg azonosság-e?

a (b c) = (a b) c.

3. Egy falu lakói három szektába tartoznak: igazmondó, felemás és hazug. Az igazmondó mindig igazat mond, a hazudós mindig hazudik, a felemás minden két egymás utáni kijelentéséből az egyik igaz a másik nem. A falu tűzoltóságán a következő telefonbeszélgetés zajlik le:

- Tűzoltóság.

- Jöjjenek, mert ég az iskola.

- Melyik szektába tartozik?

- A felemásba.

Kérdés, vajon kivonul-e a tűzoltóság?

4. Kitikkadt, elfáradt vándor érkezik a sivatagban egy útelágazáshoz. Az elágazás után az egyik út a sivatagba, a másik egy közeli oázisba vezet. Az elágazásnál egy testvérpár lakik, akik közül az egyik mindig igazat mond, a másik viszont mindig hazudik. Vándorunknak egyetlen kérdés feltevésére van lehetősége, hogy megtudja, melyik úton haladjon tovább, hogy minél előbb oázisba érkezzen. Arról viszont nincs információja, hogy melyik ember áll az útkereszteződésben, a hazudós, vagy az igazmondó. Mit kell kérdeznie, hogy a válasz alapján egyértelműen ki tudja majd választani az oázisba vezető utat?

5. Négy testvér érkezik haza egy versenyről. Az anyjuk megkérdezi, hogyan szerepeltek a versenyen. A következő válaszokat kapja:

A: sem első, sem utolsó nem lettem.

B: nem én lettem az első.

C: én győztem.

D: utolsó lettem.

Tudjuk még továbbá, hogy a 4 válasz közül 3 igaz és egy hamis. Adjunk választ a következő kérdésekre: Ki hazudott? Ki lett a győztes?

5. Kétféle gyümölcsünk van, alma és körte, három dobozban, melyekbe nem láthatunk bele. A dobozokon a következő feliratok vannak a tartalmukat illetően: alma, körte és vegyes (alma, körte). Tudjuk még azt, hogy minden felirat hamisat állít. Arra van lehetőségünk, hogy egy kiválasztott dobozba belenyúljunk, és onnan egy darab gyümölcsöt kivegyünk, a dobozba való belenézés nélkül. Hogyan járjunk el, hogy ezek után biztosra megmondhassuk, milyen lenne a dobozokon a helyes felirat.

6. Van két, ajtóval elválasztott szobánk. Az egyikben van három villanykapcsoló, a másikban három izzó, amelyeket fel lehet velük, külön-külön kapcsolni. Természetesen az egyik szobából a másikba átlátni nem lehet. A következőt tehetjük: felkapcsolhatunk tetszőleges számú kapcsolót, és egyszer átmehetünk a három izzóhoz, de ezt követően meg kell tudni mondanunk, hogy melyik izzó melyik kapcsolóhoz tartozik. Mit tegyünk, hogy a feladatot megoldjuk?

Kapcsolók algebrája.

A Boole-algebra olyan algebrai struktúra, amelyben három művelet van értelmezve. Ezekből kettő kétváltozós, mely egymásra nézve komplementeres, (azaz egymással felcserélhetők, nevezhetjük őket uniónak és metszetnek) egy pedig, egyváltozós művelet (a komplementer-képzés vagy ellentett-képzés). A halmazban két kitüntetett elem van: ezek a minimális és maximális elem (tekinthetjük üres halmaznak, a másodikat alaphalmaznak). A két kétváltozós műveletre a de Morgan azonosság érvényes.

Példák Boole-algebrára: halmazalgebra, eseményalgebra, ítéletek algebrája, osztók algebrája (az osztók, legkisebb közös többszörös, a legnagyobb közös osztók), kétállapotú kapcsolók algebrája.

A kapcsolók algebrájában az elektromos áramkörök azon részeit tüntetjük fel, amelyben kétállapotú kapcsolók találhatók. A kapcsolók egymáshoz való kapcsolódása adja a logikai működést. Egy-egy kapcsoló több példányban is szerepelhet az áramkörben. Ebben az esetben úgy kell elképzelni, hogy ezek a kapcsolók kis rudakkal össze vannak kötve, így egyszerre működnek. A kapcsolókat két különböző állapotban rajzolhatjuk fel: alapértelmezésben a kapcsoló nyitott, ha a negációját szeretné feltüntetni, akkor zártan rajzoljuk le. Azaz:

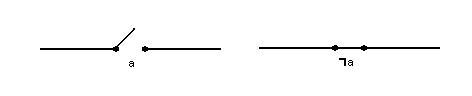
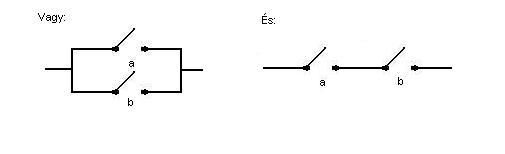
Mivel a logikában tanult tétel értelmében bármely logikai művelet - akár egy, akár többváltozós - kifejezhető csak az "és" a "vagy" és a negáció, valamint a zárójel segítségével, így a kapcsolóalgebrában is csak e két alapművelet megvalósítását kell megismernünk, a többi művelet már ezekkel megadható. Ezek megvalósítása pedig, a párhuzamos és a soros kapcsolás. Mivel két párhuzamosan kötött kapcsolóból, ha az egyiket bekapcsoljuk, akkor már vezet, a párhuzamos kapcsolás a "vagy" műveletet tudja megvalósítani. Mivel két sorba kötött kapcsoló csak akkor vezet, ha mindkettő zárva, a soros kapcsolás lesz az "és" megfelelője. Rajzban:

A következőben megadjuk mind a 16 (a sorszám az előzőekben megismert táblázatnak megfelelő), legfeljebb kétváltozós logikai művelet kapcsolóábráját:

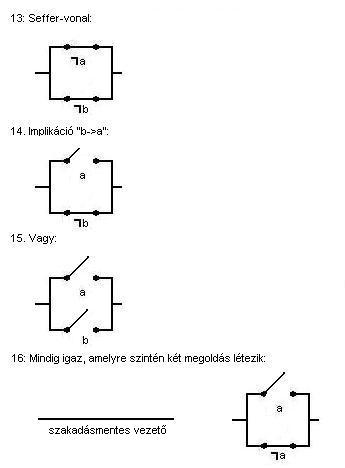
Feladatok:

1. Van egy hajszárítónk, amelyen két kapcsoló található. Az egyik beindítja a villanymotort, a másik a fűtőszálat kapcsolja. A hajszárító hideg és meleg levegőt is tud fújni, a fűtőszálat viszont egyedül bekapcsolni nem lehet (mert ha lehetne, elégne). Adjuk meg a kapcsolók, a villanymotor és a fűtőszál egymáshoz való kapcsolódását.

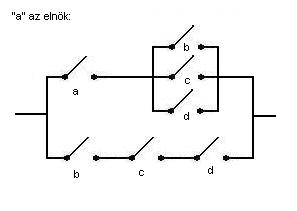
2. Van egy négytagú szűri. A zsűri az eléje kerülő produkciókat vagy továbbengedi a következő fordulóra, vagy nem. A továbbjutás feltétele a többségi szavazat. Ha a zsűriben a szavazatok száma megegyezik, akkor az elnök szava dönt. Tervezzünk olyan kapcsolókból álló áramkört, amely automatikusan dönt (a szavazatok alapján) a továbbjutásról. (Egy kapcsoló több példányban is szerepelhet az áramkörben.)

A 2. feladat megoldása:

Logikai áramkörök

Logikai áramkörök megvalósításának eszközei lehetnek: kapcsolók, relék, elektroncsövek, félvezetők, integrált áramkörök. A relék (amelyek elektromágnest tartalmaznak) gyakorlatilag elektromechanikus kapcsolók. Az elektroncsövek vagy vákuumcsövek ma már kevésbé használatos olyan áramköri elemek, amelyekben a vezetés az izzó katódból a vákuumba kilépő elektronok mozgásán alapszik. A negatív katóddal szemben helyezkedik el a pozitív anód. További elektródák (rácsok) segítségével az elektronáram vezérelhető. Az elektroncső használható erősítő elemként vagy kapcsolóként. Mai elektronikai eszközeinkben már kevés található belőlük, de a TV képernyője még többségében katódsugárcső. A másik elektronikus kapcsolóelem a tranzisztor, mely félvezetők egyik fajtája.

A következő táblázatban az elektroncsövek és félvezetők összehasonlítását láthatjuk:

Tulajdonság	Elektroncső	Félvezető
Anyag	Üveg, fémek, vákuum	Si vagy Ge
Üzemi hőmérséklet	100 celsius fok körül	Szobahőmérséklet körül
Méret	20*20*80 mm	1-2 mm
Üzemidő	1000 óra	10 év
Energiafelhasználás	10 W	10-20 mW

A félvezetők alkalmazásának előnyei: kis méret (chip: morzsa), kis energiafelhasználás, hosszú ideig megbízható működés, olcsó előállítás, nagytömegű gyártás, sokoldalú felhasználhatóság, olcsóbb szerviz.

Félvezetők tulajdonságai: olyan anyagok, amelyeknek szobahőmérsékleten kicsi a vezetőképessége (értéke a vezetők, és szigetelők között van), hőmérsékletük emelésével a vezetőképessége nő. Vezetőképességüket szobahőmérsékleten is jelentősen befolyásolja a benne lévő szennyező atomok mennyisége. Leggyakoribb félvezető anyagok a Germánium és újabban a Szilícium. Mindkettő 4 vegyértékű, kristályos anyag, tiszta állapotukban jó szigetelők. A 4 vegyérték azt jelenti, hogy a külső elektronhéjon 4 elektron foglal helyet. Ezek a környezetükben lévő további 4 atom 1-1 külső elektronjával nemesgáz állapothoz közeli, stabil elektronhéjat alkot. Ezért vezeti rosszul az áramot. Szennyezve a vezetőképesség nagyot változik. Kétféle szennyezést ismerünk: ha olyan anyaggal szennyezzük, amely 3 vegyértékű, (pl: indium), akkor p típusú szennyezett félvezetőt kapunk; ha olyannal, amely 5 vegyértékű (pl: arzén), akkor n típusú szennyezett félvezetőt kapunk.

Félvezetőkből készült áramköri elemek: termisztorok, diódák, tranzisztorok, integrált áramkörök.

A termisztorok olyan egyrétegű félvezető elemek, melyek a félvezető negatív hőmérsékleti együtthatóját kihasználva, hőmérőkben hőmérsékletmérésre, illetve negatív visszacsatolású áramkörökben hőmérsékletstabilizálásra használhatnak.

A diódák kétrétegű félvezető elemek. Két különbözőképpen szennyezett félvezető rétegből áll. A p-n átmenet viselkedése árammentes állapotban olyan, hogy a határréteg a különböző potenciálú rétegek hatására töltéshordozóktól mentessé válik, kiürül. A mozgékonyabb elektronok átmennek a p rétegbe. Olyan potenciálgát alakul ki, mely a további áramlást megakadályozza. A diódát egyenáramú áramkörbe kétféleképpen lehet bekötni. Ha a p réteget a pozitív, az n réteget a negatív pólusra kötjük, akkor a dióda nyit, a potenciálgát lecsökken, a határréteg elvékonyodik, a dióda vezet. Ha a polaritást megcseréljük, azaz a p réteg negatív, az n réteg pedig, pozitív pólusra kerül, akkor a határréteg megnő, kialakul egy töltésmentes, szigetelő réteg, a dióda lezár, azaz nem vezet. Ha a diódát váltakozó áramú áramkörbe kötjük, akkor is csak egyik irányba vezet, mindig csak akkor, ha nyitóirányú feszültség kerül rá. Dióda alkalmazásai: egyenirányítás (egy-utas és két-utas: Greatz-híd, polaritás-védelem, demodulálás, feszültségstabilizálás (kihasználva, hogy egy határréteg csak megfelelő feszültség hatására nyit, vagy zár).

A dióda rajzjele (a felfedezhető nyíl a technikai áramirányt jelzi):

A tranzisztorok háromrétegű félvezető elemek. A legegyszerűbb felépítésű tranzisztorok kétfélék lehetnek: pnp és npn. Az elnevezések a rétegek elhelyezkedését jelentik. A három réteg elnevezése: emitter (kibocsátó), bázis és kollektor (befogadó). A felépítések és a megfelelő rajzjelek:

Az emitter mindig erősen, a kollektor mindig gyengén szennyezett, a bázis, pedig mindig vékony réteget jelent az emitter és a kollektor között. A tranzisztor alapkapcsolása a földelt emitteres kapcsolás, ekkor a pnp tranzisztornál az emitter pozitív, a kollektor negatív, az npn tranzisztornál természetesen fordítva.

A bázis az emitter – feszültségéhez közeli, tőle kb. 0,4 V-ra van, vagy ennél jóval nagyobb, a tranzisztor alkalmazásától függően. Ezen feszültség (0,4 V) környékén nyit ki a tranzisztor (ellenállása jelentősen csökken), vagyis indul meg az áram az emitter és kollektor között.

A tranzisztort két lényegesen különböző módon használhatjuk: vagy kapcsolóként, vagy erősítőként. Kapcsolóként a bázisfeszültség 0,4 V körüli értékre van kiélezve, míg erősítőként a bemenetre sokkal nagyobb feszültséget kell juttatni. Ha tehát a bázisfeszültség 0,4 V alatti, akkor nincs emitter – kollektor áram (ellenállása nagy), a tranzisztor lezár, e feszültség felett kinyit, azaz kapcsolóként működik, kétállapotú rendszerként használható.

Ha bázisra 0,4 V-nál jóval nagyobb jelet juttatunk és a kimenő jelet, a kollektorról vesszük le, akkor invertáló erősítőt kapunk. Ha tehát a tranzisztort földelt emitteres kapcsolásban használjuk, akkor a kollektoron (mint invertáló kimeneten) a bázisra adott feszültséggel arányos (az erősítési tényezőtől függő) jel jelenik meg. Ekkor a tranzisztor analóg erősítőként dolgozik. Ha a jelet az emitter-körbe helyezett ellenállásról, akkor nem invertáló az erősítő. Ha több tranzisztort egymásután kötünk, többfokozatú erősítést valósíthatunk meg. Az ilyen erősítőben a jel energiája minden fokozatban tovább növekszik.

Ha a tranzisztort kapcsolóként hasznosítjuk, akkor a vezetési állapotnak 1-et (vagy logikai igazat) feleltethetünk meg, lezárt állapotának pedig, 0-át (logikai hamisat). Több tranzisztort, diódát alkalmazva logikai áramkörök építhetők fel.

Integrált áramkörök: egy félvezető lapkán előállított több száz, ezer vagy manapság már több millió félvezető elem, amely valamely feladat érdekében célszerűen együttműködik. Integráltságuk szerint megkülönböztetünk: SSI, MSI, LSI, VLSI, SVLSI áramköröket. Működési alapelvük szerint két nagy csoportra oszthatók: analóg és digitális áramkörök.

Az analóg IC-k sok tranzisztort, diódát, ellenállást és kondenzátort tartalmaznak. Bennük az elektromos jel energiatartalma hasonlóan nő, mint a tranzisztorban - amikor erősítőként működik.

Digitális IC-k, vagy TTL (tranzisztor-tranzisztor logika) áramkörök. Olyan, főleg tranzisztorelemekből felépített integrált áramkörök, amelyek a bemenő feszültségértékeket logikai 0-nak vagy 1-nek veszik, belső felépítésüktől függően logikai műveleteket végeznek (szokás műveleti erősítőknek is nevezni őket), és kimenetük is logikai 0 vagy 1. Vannak olyan integrált áramkörök, melyekben olyan nagyszámú logikai áramkört képeztek ki, hogy összetett feladatokat egyedül képesek elvégezni, pl.: számtani műveleteket végezni. Ilyenek a zsebszámológépekben található IC-k.

A logikai áramkörök feszültségértékeit kétféle logika szerint szokták használni. Pozitív logika esetén:

L = kis feszültség (Low voltage) = logikai 0,

H = nagy feszültség (High voltage) = logikai 1.

Negatív logika esetén az előző fordítottja érvényes. (L=1, H=0).

A legegyszerűbb logikai áramkörök (illetve azok részei), egy-egy logikai műveletet valósítanak meg. Ezeket szokás kapuknak (gate) is nevezni. A következő kapukat ismerjük:

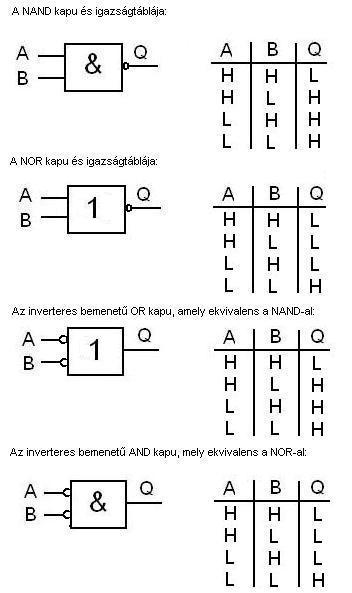
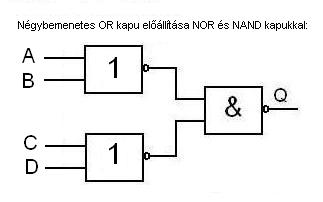
A legegyszerűbben előállítható kapuáramkör az invertáló (4 db tranzisztor) és a NAND kör. Ennek következtében nagyon gyakran a logikai áramköröket NAND körök segítségével kell előállítani. Erre mutatunk most néhány példát.

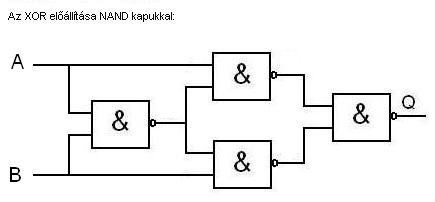
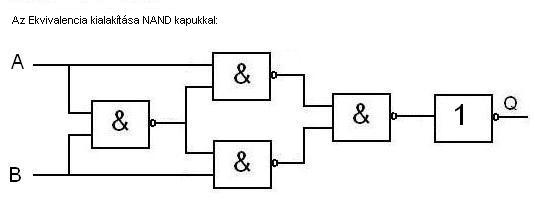
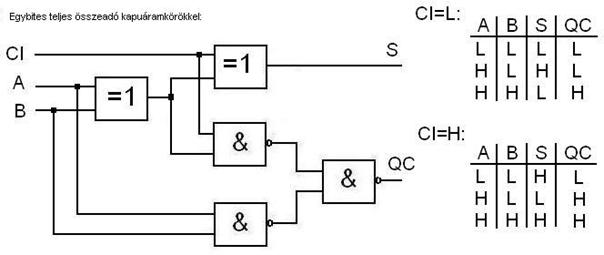
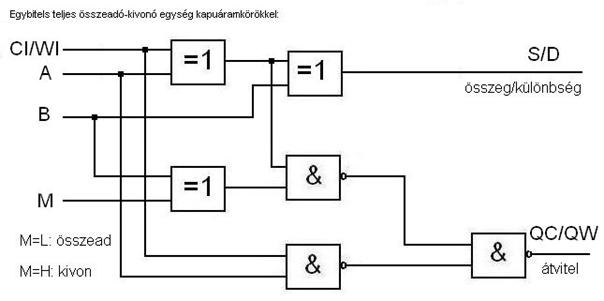
Ennyit ízelítőként a kapuáramkörökről. A legfontosabb az, hogy tudjuk elolvasni a tanult rajzokat, illetve lejátszani egy-egy igazságtábla részletet, a logikai értékek beállásának megállapításával.

A továbbiakban csak felsorolásszerűen megemlítjük, hogy milyen feladatokat kell megoldani logikai áramkörökkel digitális rendszerekben:

- összeadók,

- kódolók,

- tárolók (bistabil áramkörök, ROM és RAM),

- impulzusgenerátorok (astabil áramkörök),

- impulzusszámlálók,

- impulzusosztók és -szorzók,

- léptető tárolók (bitforgatás),

- dekódolók,

- multiplexerek (adatkiválasztók),

- párhuzamos-soros és soros-párhuzamos átalakítók,

- kijelzők (hétszegmenses kijelzők),

- aritmetikai áramkörök.