Izogonális pont (8)

Egy geometriai szélsőérték feladat

Feladat: Adott a síkban n darab pont. Keresendő az a pont, amelyből az adott pontokba húzott szakaszok hosszának az összege – a sík bármely pontjára nézve – a lehető legkisebb.

Mint ahogy azt az eddigiekből is tudhatjuk, a távolságösszeget leíró kétváltozós függvényünk a következő alakú:

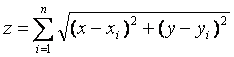
Ebben a részben néhány konkrét esetre ezt a felületet fogjuk megrajzoltatni egy programmal. Az ábrázoláshoz a kavalieri-féle axonometriát fogom használni. Az (x, z) sík párhuzamos a rajz síkjával. Az y tengely a másik két tengellyel a rajzon 45 fokos szöget zár be, amelyen a skálázás a másik két tengely gyök 2-ed része. Haladjunk a pontok száma szerint.

n=1

Egy pont esetén ez nagyon egyszerű, könnyen felismerhető a kör egyenlete:

Ennek térbeli kivetítése, ha a sugarakat folyton növeljük, egy kúpfelület, melynek csúcsszöge 90 fok.

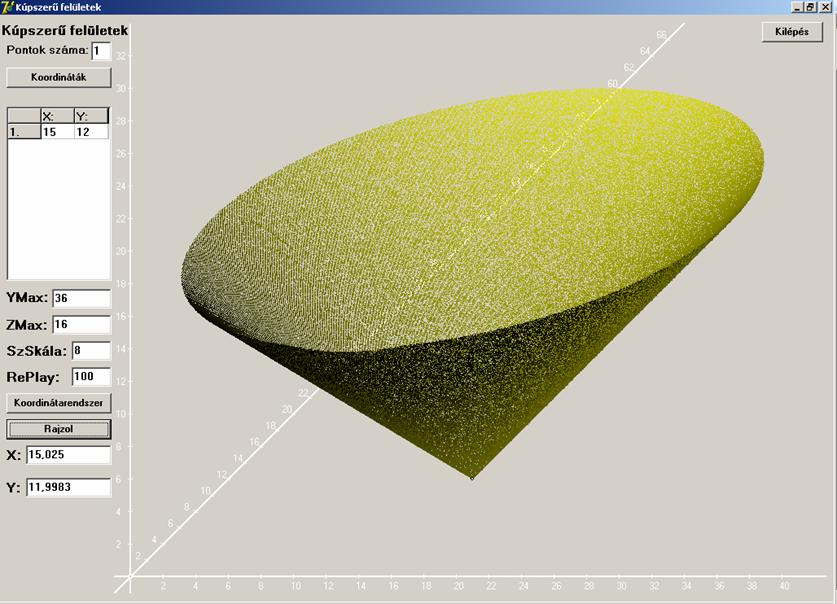
n=2

Két pont esetén is kitalálható, hogy mi az egyenlet. Ekkor ugyanis két ponttól vett távolságösszegnek kell állandónak lenni, ami nem más, mint az ellipszis. Ennek a térbeli kivetítése egy olyan felület, melynek két csúcspontja van, a két pont fölött. A felület itt egy szakasszá torzul, minden más (x, y) síkkal párhuzamos síkmetszete ellipszis. A program megkeresi, és az ábrázoláskor feltünteti a minimum helyeket (kék színnel) és a minimális szakaszokat (fehérrel). Így volt ez egy pont esetén is. Ott azért nem látszott az ábrán, mert egybeesett a kúp csúcspontjával. Itt látható mindez. Azért egy kis sajátosság itt is van. A minimumhely a szakasz bármely pontja lenne, de csak egyet ábrázol (csak egyet jegyez meg a program, végtelen sokat egyébként sem tudna).

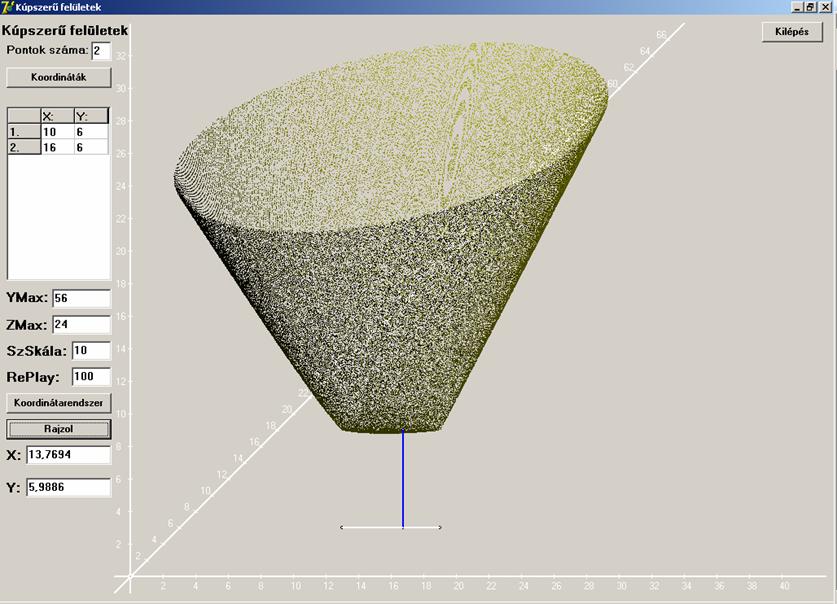
n=3

Először a három pont egy egyenesre illeszkedjen. A feladat megoldása a középső pont lesz. Ennek a kúpszerű felületnek már nincs kör vagy ellipszis metszete még akkor sem, ha ez az ábrán mégis annak látszik. Minél messzebb vagyunk ugyanis a csúcsoktól, az (x, y) síkkal párhuzamos síkmetszete annál inkább hasonlít a körre vagy ellipszisre, de soha nem lesz sem kör, sem ellipszis.

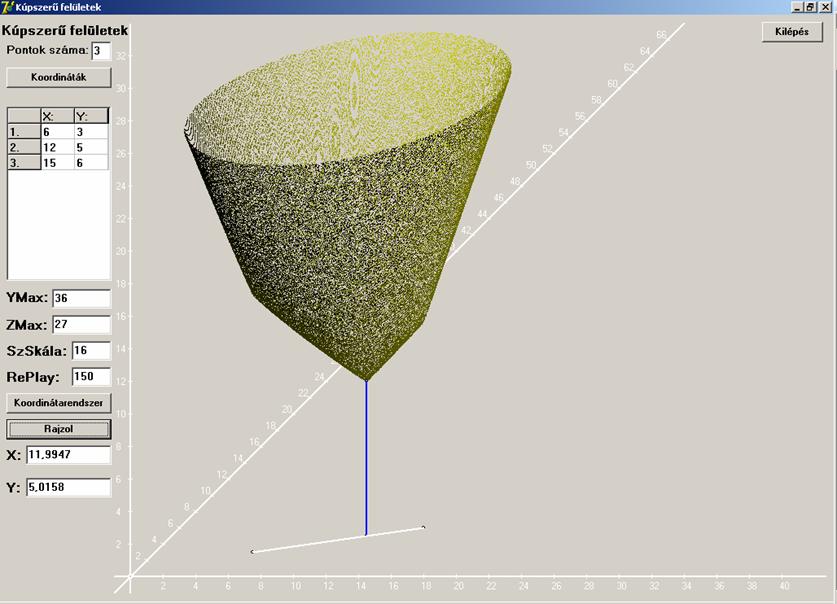
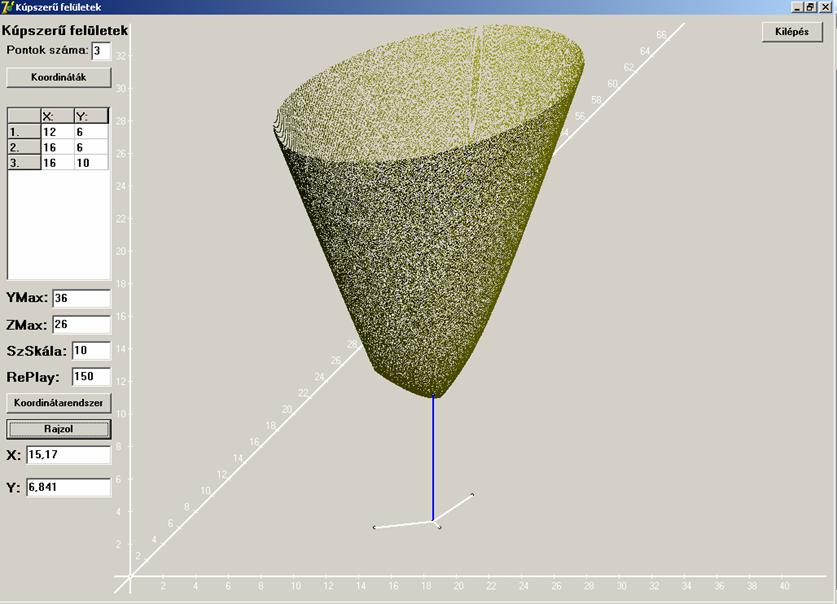
Második esetként a három pont egy egyenlő szárú derékszögű háromszöget határoz meg. Íme a függvény képe:

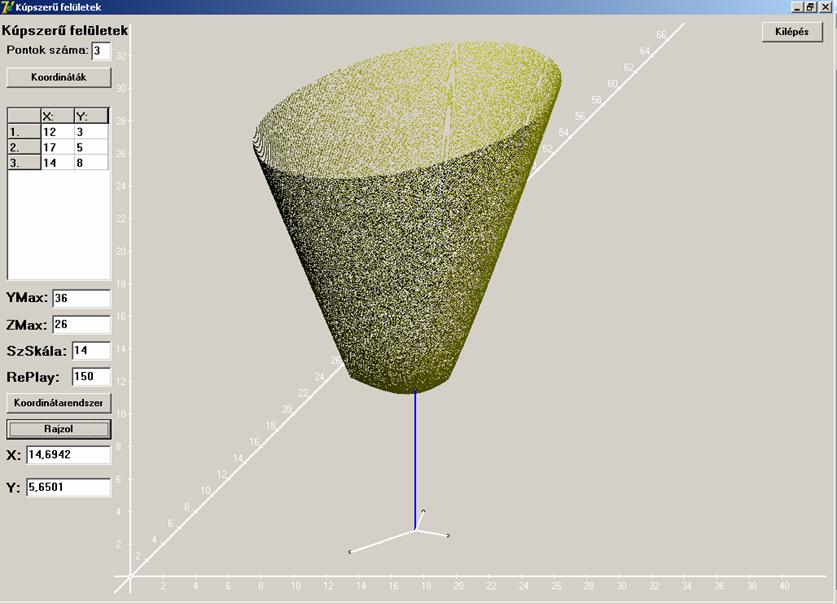
Harmadik esetként egy általános háromszöget határoznak meg, melynek nincs 120 fokos, vagy annál nagyobb szöge.

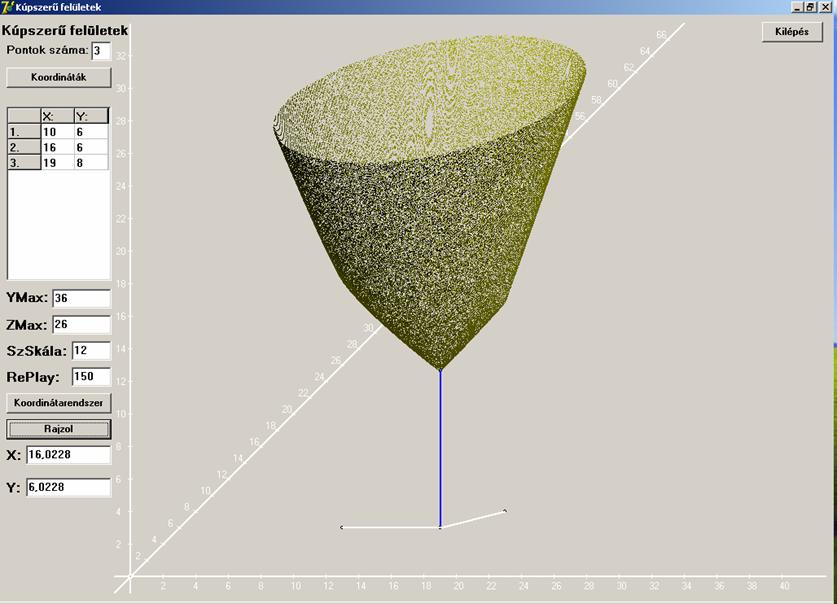
Most a háromszögnek van 120 foknál nagyobb szöge:

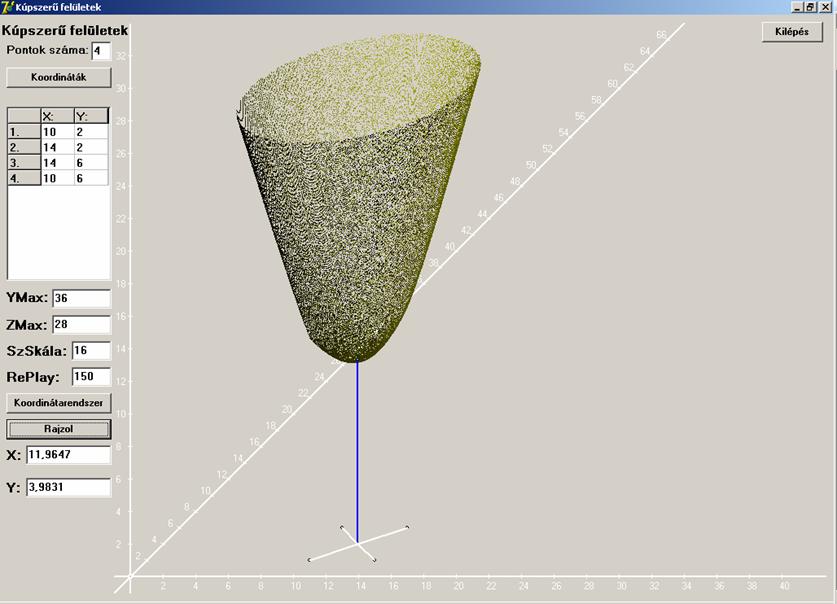
n=4

Kezdjük egy négyzettel:

Legyen a négyszög konkáv:

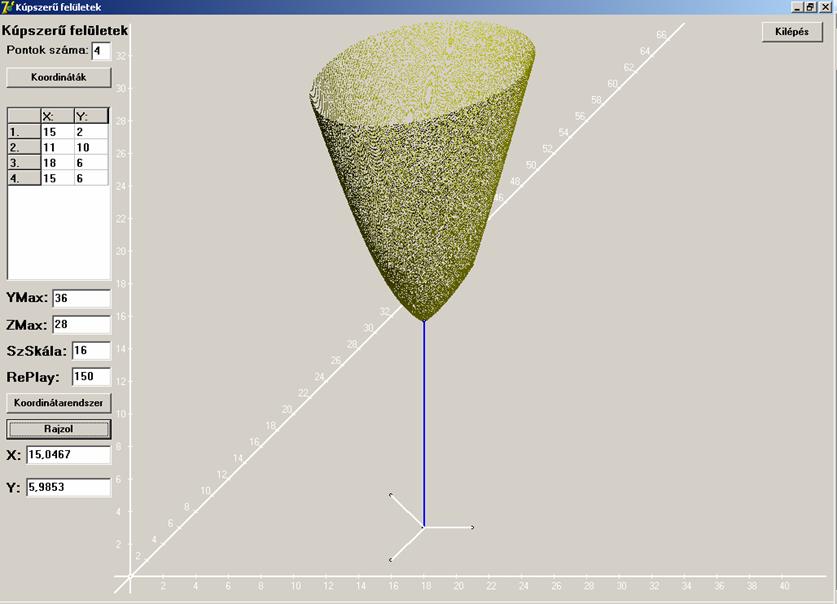
n=5

Végül legyen az 5 pont általános helyzetű, de konvex ötszöget alkosson:

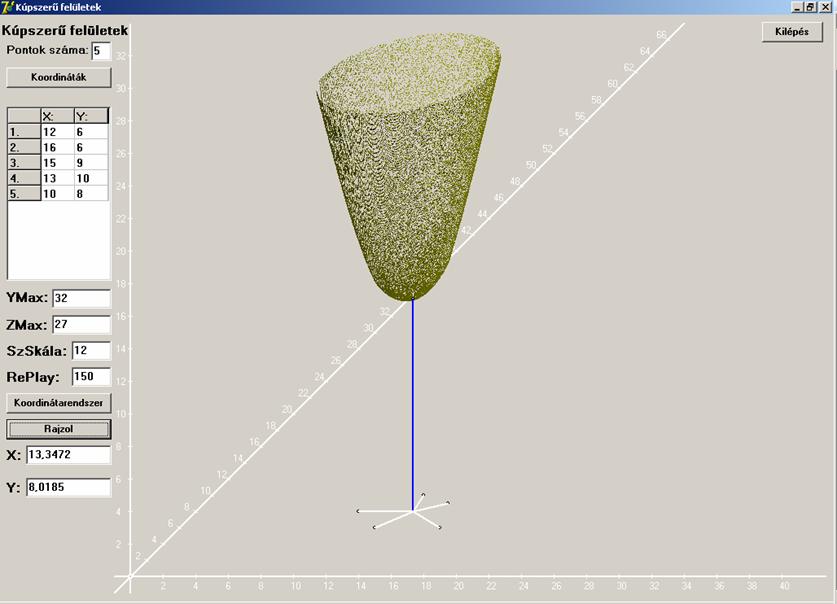
Végignézve a felületeket, túl sok változatosságot nem láthatunk rajtuk. Mindegyiknek van egy csúcspontokkal teli „alsó” része, a „felsőbb” részeken pedig mind hasonlóan viselkedik, olyan mintha kúp lenne. Személy szerint én nem is vártam sokkal másabb ábrákat. Talán, ha csak a csúcspontok közeli részeket ábrázoltam volna jobban kinagyítva, akkor változatosabb lett volna az összkép. Ha a továbbiakban ilyeket készítek, akkor elhelyezem ezen a lapon.

Következő lap: http://gorbem.hu/MT/Izogonalis9.htm