Izogonális (7)

 

„Kúpos Integrál”

 

Ezen a lapon az IMT jelentős általánosításáról olvashatunk. Az eddigi feladatokban véges összegzések szerepelnek a kitűzött feladatokban. Arra gondoltam, hogy a határozott integrál is egyfajta összegzés, csak éppen végtelen-sok tagú összeget jelent. Mi lenne, ha a távolságösszeget és az integrált valahogy összekötnénk. Első gondolatként egyszerűen csak vennénk egy abszolút érték függvény határozott integrálját egy [a, b] intervallum felett. Ugyanakkor függvényt szeretnék kapni, nem egy konstanst. Körülbelül így:

 

 

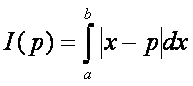
Ebben a függvényben a p a független változó. Természetesen most is minimumot keresünk. Könnyen belátható, ennek az I(p) függvénynek a minimuma a p0 = (a+b)/2 értéknél van, azaz a határozott integrál intervallumának a felénél, a határok számtani közepénél. Ugyanis:

 

 

Valóban, a függvény minimuma az intervallum közepénél van. Nos, lépjünk tovább ennél az egyszerű esetnél. Mit tehetnénk? Például azt, hogy megszorozzuk az integrandust egy tetszőleges, ámbár elég jó tulajdonságú függvénnyel. Majd ezután is tegyük fel újra a kérdést: hol lesz a keletkezett függvénynek a minimuma? Azaz bizonyítsuk be a következő tételt:

 

Tétel: Legyen

 

 

tehát egy, az [a, b] zárt intervallumon értelmezett pozitív értékű valós függvény, amely rendelkezik a következő tulajdonságokkal:

 

a) az f(x) kétszer folytonosan differenciálható,

b) létezik primitív függvénye, amelyet F(x)+c –vel jelölünk,

c) a primitív függvénye folytonosan deriválható.

 

Legyen továbbá:

 

 

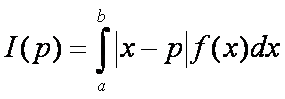
ahol p egy valós független változó, és 0<a<b valós számok.

 

Lássuk be a következő állítást: az I(p) függvény minimumhelye:

 

 

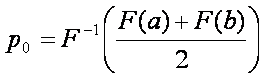
Bizonyítás. Először alakítsuk át az I(p) függvényt:

 

 

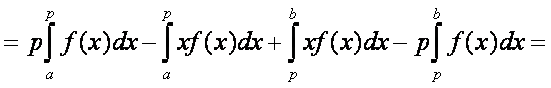
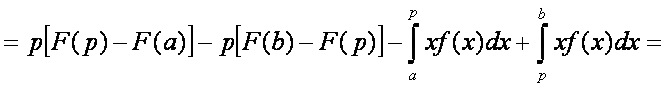
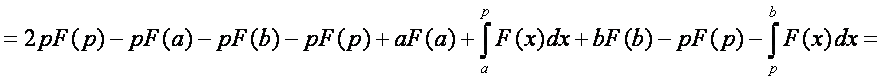
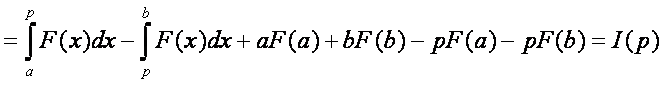
Képezzük az I(p) első deriváltját (jelölje G(x)+c az F(x) primitív függvényét):

 

 

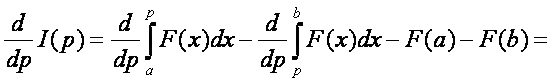
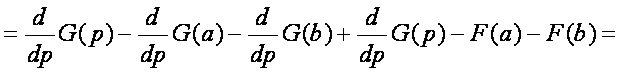
Ugyanis G-nek a deriváltja F, a G(a) és G(b) pedig konstans, tehát deriváltja nulla. Ebből már nyilvánvaló, hogy a szélsőérték helye valóban:

 

 

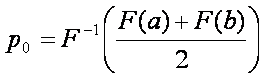
Annak érdekében, hogy megerősítést nyerjen a szélsőérték helye és minősége, egy kicsit tüzetesebben vizsgáljuk meg az I(p) függvényt. Ameddig lehet, vizsgálódjunk általánosan, aztán ábrázoljuk géppel néhány konkrét esetre a függvényeket.

 

Nézzük tehát, milyen lehet az I(p) menete. Számítsuk ki értékét az intervallum végpontjaiban. Majd írjuk fel az egyenletét a kisebb végpont előtt: I-(p), és a nagyobb végpont után: I+(p).

 

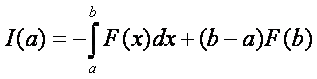
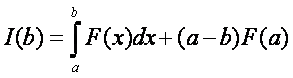
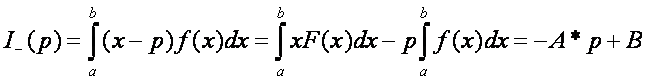
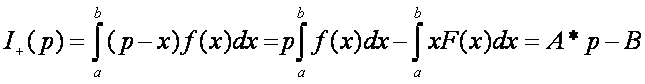
ahol: 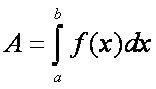        és    

 

A kapott eredmények alapján az I(p) mente már vázolható. Az x<a értékekre a függvény képe egy félegyenes, meredeksége –A. Az x>b értékekre szintén félegyenes, melynek meredeksége A. Ha a és b helyen ismerjük az függvény értékét, akkor ezek a félegyenesek már meg is rajzolhatók.

 

Az intervallum feletti alak elemzéséhez vegyük az I(p) második deriváltját.

 

 

Ebből az látszik, hogy az intervallum felett a függvény alulról konvex, amelynek minimuma a fentebbi p0 helyen van. Nézzük meg, hogy az I(p) deriválható-e a szakasz végpontjaiban. Ehhez a derivált értékét nézzük meg a végpontokban:

 

 

A két meredekség egymás negatívja. A határozott integrál definíciója alapján:

 

 

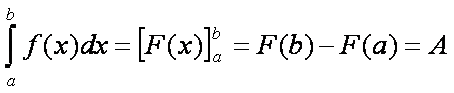
Látható, hogy a kétféleképpen kiszámított meredekség minkét végpontban azonos a félegyenesek meredekségével, így az I(p) függvény értelmezési tartományának minden pontjában differenciálható.

 

Nézzük meg még jobban a két lineáris szakaszt. Ezek meghosszabbítása az x tengelyt ugyanabban a pontban metszik, nevezetesen az:

 

 

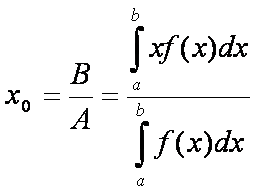
pontban. Ajaj, ez nagyon ismerősnek tűnik. Valóban, ez annak a síkidom súlypontjának az x koordinátája, amelyet az x tengely, az x = a, x = b egyenesek és az y = f(x) függvény grafikonja határoz meg. Úgy látszik, hogy minden mindennel összefügg. A teljesség kedvéért a súlypont y koordinátája:

 

 

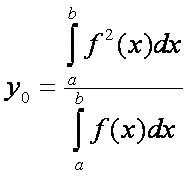
Térjünk vissza egy kicsit a p0 értékét megadó egyenletre és írjuk vissza integrálra.

 

 

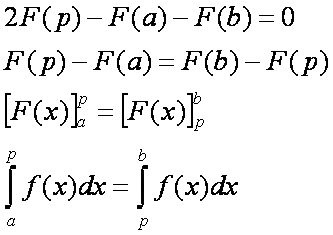
Azaz a p0 az [a, b] szakasz olyan pontja, amelyen átmenő x = p0 egyenes az f(x) alatti területet felezi. Nézzük meg, hogy a p0-ra valóban igaz-e, hogy az [a, b]-re esik:

 

 

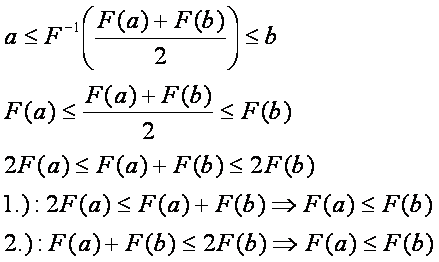
A levezetés első lépése csak akkor helyes, ha az F(x) szigorúan monoton növekvő, ami viszont abból következik, hogy egy pozitív valós függvény primitív függvénye. Azaz a p0 az [a, b] intervallumra esik. A monotonitást az 1.) és 2.) sor is kifejezi.

 

Értelmezve az eddigi eredményeket, azt mondhatjuk, hogy a függvény minimuma az intervallum végpontjainak a primitív függvénnyel meghatározott additív függvényközepénél található. A függvényközepek aktuális alakja az f(x) konkrét megválasztásától függ.

 

Megjegyezném, hogy Honlapomnak a Matematika menüpont alatti, a Közepek lapján leírtaknak, az n = 2 esetét látjuk viszont a p0 képletében. Annak eldöntését, hogy ez véletlen-e vagy sem, az olvasóra bízom. Összevetve a Közepek nevű lapon találhatókkal, röviden felsorolnám az f(x) néhány speciális esetét (a teljesség igénye nélkül, és feltételezve, hogy a és b mindenütt megengedett értéket vesz fel).

 

1.) 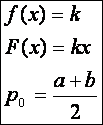 (Számtani közép.)

 

 

2.)  (Hatványközép, n=1 –re négyzetes közép.)

 

3.) 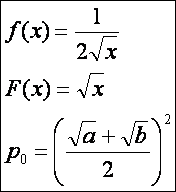 („Inverz” négyzetes közép.)

 

4.) 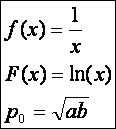 (Mértani közép.)

 

5.) 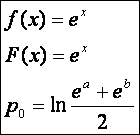 (Logaritmikus közép.)

 

6.) 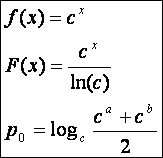 (Általános alapú logaritmikus közép.)

 

7.) 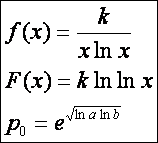 (Exponenciális közép)

 

8.) 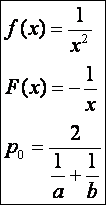 (Harmonikus közép.)

 

Amint látható, minden közismert közepet is megkaptunk szélsőérték helyként.

 

Összefoglalva I(p) egy olyan, az abszolút érték (y = |x|) függvényhez hasonló függvény (ha az [a, b] intervallum hossza tart a nullához, akkor egyre jobban hasonlít rá), amely folytonos, minden pontjában deriválható, alulról konvex, és abszolút minimumát az [a, b] intervallum p0 belső pontjában veszi fel. Mindez, amit eddig megtudtunk a témáról, indokolta számomra a választott alcímet, és az, hogy jobbat nem találtam. Olyan mintha egy ponttól (p0-tól) a mínusz és a plusz végtelenbe is növekedne a függvénynek az értéke, ráadásul a szakaszon kívül lineárisan. Talán ezért az elnevezés. Természetesen nem lett volna kötelező elnevezni a függvényeket, egyszerűen csak azt mondhattam volna, hogy vizsgáljuk meg a fentebb leírt típusú integrálokat.

 

A továbbiakban nézzünk konkrét f(x) függvényeket, amelyekhez tartozó I(p) függvényeket ábrázolni is fogjuk.

 

 

 

Térjünk tehát át a számítógéppel történő ábrázolásra. Ábrázoljuk a várhatóan legegyszerűbb I(p) függvényt. Azaz először legyen f(x) = k. Határozzuk meg a lineáris rész együtthatóit, A- és B-t.

 

 

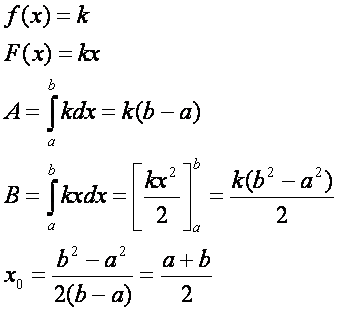
Írjuk fel I(p)–nek az [a, b] intervallum feletti részének a képletét.

 

 

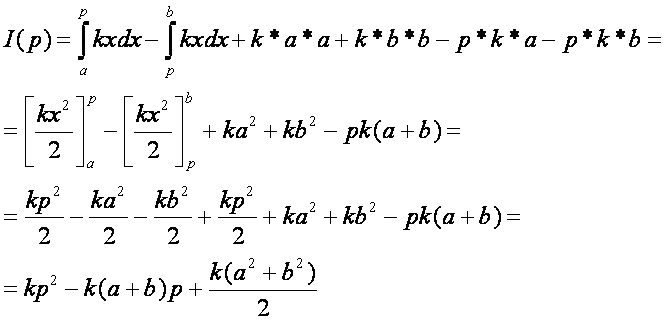
Látható, hogy a függvény most egy parabolaág. Számítsuk ki az I(a) és I(b) értékeket.

 

 

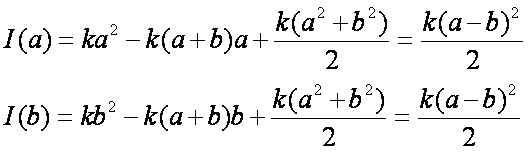
Mint látható I(a) = I(b). Ez a további függvényeknél nem lesz így, különbözni fognak.  Az I(p) deriváltja:

 

 

Ennek zérus helye valóban az a és b számtani közepe:

 

 

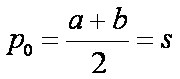
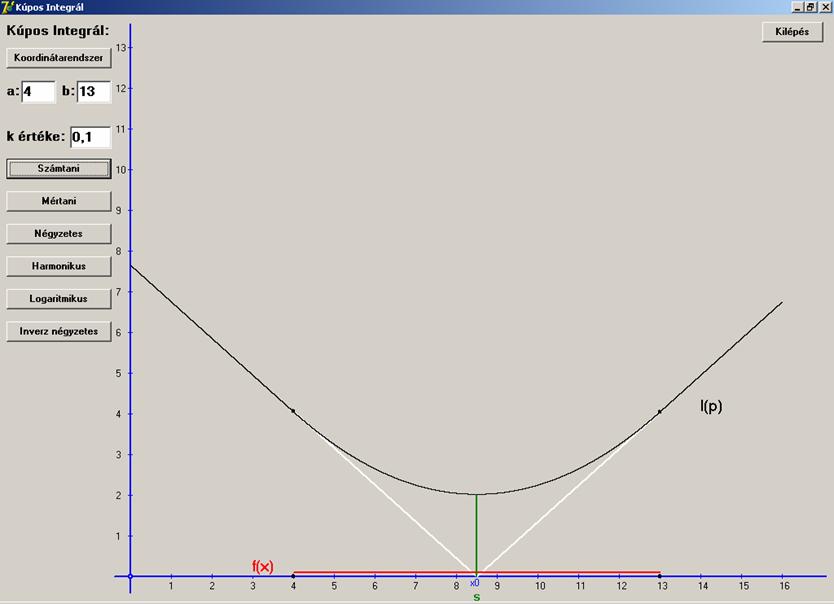
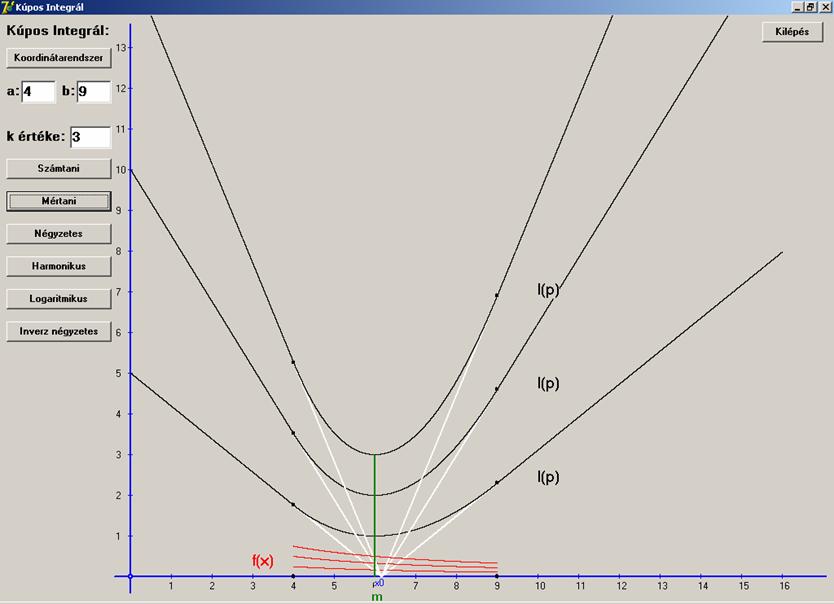
Ezek alapján a program már meg tudja rajzolni a függvényt. Lássuk mit kapunk a következő értékekre: [a, b] = [4, 13] és f(x) = 0,1. Az ábrán az f(x) függvény piros színnel van rajzolva és jelölve is. A grafikon fehérrel rajzolt egyenes szakaszai az I(p) lineáris részeinek a meghosszabbítása az x tengelyig. Látható, hogy ezek ugyanabban az x0 pontban metszik a tengelyt. Sőt ez az s ponttal is egybeesik. Hogy ez mennyire általános, az majd kiderül. Ez a p0, csak s-sel jelöljük, utalva a számtani középre. A további közepeknél, ott is utalva a közép típusára, más-más lesz ennek a pontnak jele. Zölddel jelöljük az I(p) minimumát. Az I(p) grafikonján a fekete pontok a lineáris szakaszok végpontjai, azaz az [a, b] intervallum végpontjainak megfelelő pontok. A jelölési rendszer a továbbiakban ugyanaz lesz, mint most.

 

 

Nézzük mit kapunk a ha: [a, b] = [4, 7] és f(x) = 2.

 

 

Nézzük mit kapunk a ha: [a, b] = [6, 9]. Ezen az egy intervallumon ábrázoljuk az I(p)-t az f(x) = 2,  f(x) = 1,5, f(x) = 1 és végül az f(x) = 0,5 értékek mellett, ugyanabban a koordinátarendszerben. A nagyobb értékekhez tartozó I(p) függvények is nagyobb értékeket vesznek fel.

 

 

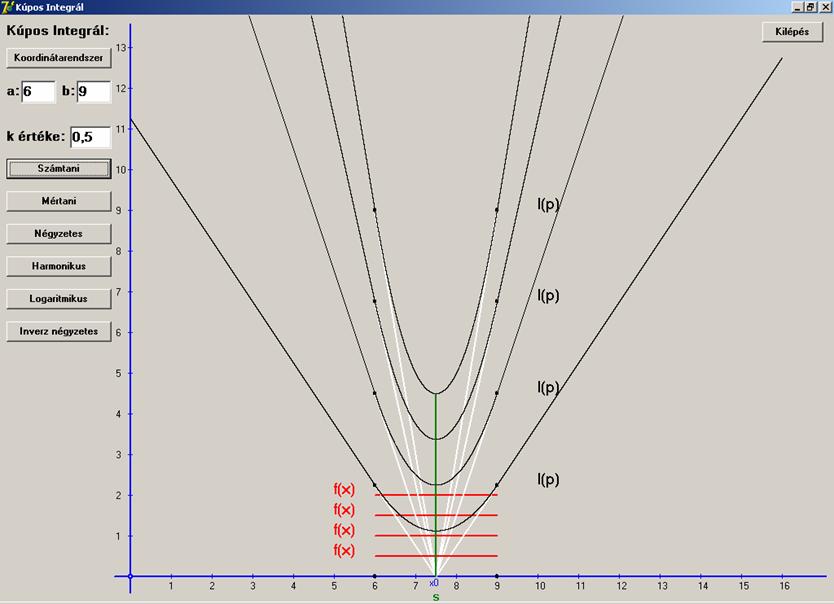
Vajon hogyan változik a függvény alakja, ha az f(x) = 1,5 -t nem változtatjuk, viszont az [a, b] intervallumot igen?

 

 

Az első két esetben az intervallum hossza sem változott. Eredménye az lett, hogy a függvény alakja sem változott, csak 5-el eltolódott (mint az intervallum). Harmadik esetben az intervallumot rövidítettem, akkor a csúcspont eltolódása kétirányú lett (jobbra 4,5 és lefelé 2 egységgel) és a lineáris részek meredekségének nagysága csökkent (nyitottabb lett a V alak). Minden ábrázolt esetben az x0 azonos volt p0-al. Vajon a további közepeknél is ez lesz a helyzet?

 

Az ábrázolás természetesen nem bizonyítja, de aránylag jól szemlélteti, hogy a függvények minden pontban differenciálhatók. Mindegyiknek az alakja nagyon hasonlít a parabolához (az intervallumon az is), hiszen ha a csúcsponttól elég messze vagyunk, akkor a parabola egyre jobban hasonlít az egyeneshez (de soha nem azonos vele).

 

 

 

Másodiknak legyen olyan a függvény, amelynek következtében a p0 a mértani közép lesz. Ez a függvény az f(x) = k/x. Határozzuk meg a szükséges értékeket.

 

 

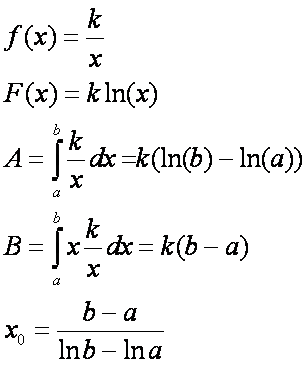
Ezek után írjuk fel az I(p) függvényt.

 

 

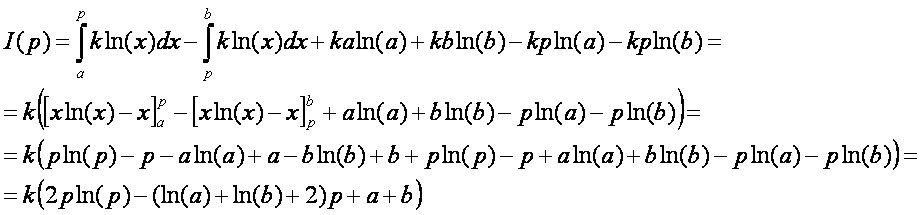
Írjuk fel az I(p) függvény deriváltját és határozzuk meg a zérus helyét.

 

 

Ezek után nézzünk néhány grafikont. A minimumot az m (mértani közép) jelöli. Először k = 1, és változtassuk meg az intervallumot [2, 8])-ról [3, 12]-re. Ezt kapjuk:

 

 

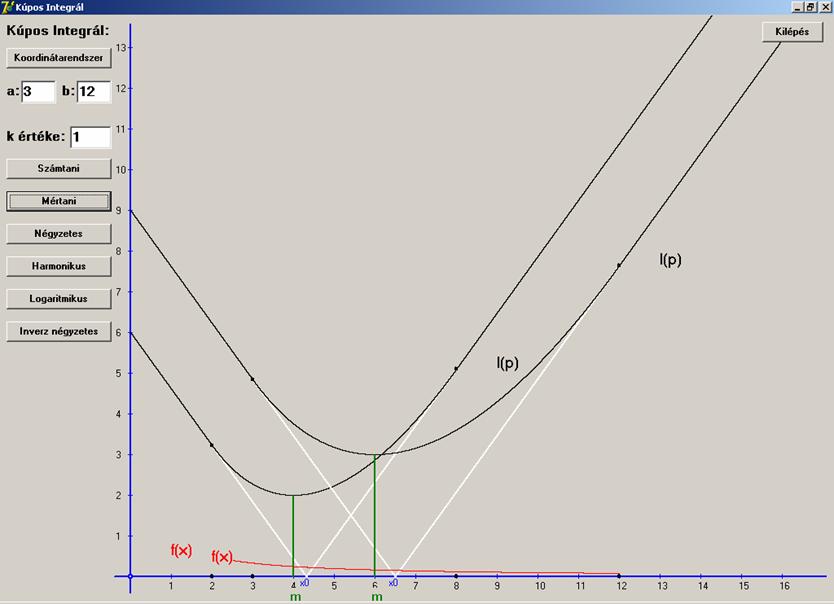
Jó látható, hogy mértani közép esetén az x0 már nem egyenlő a p0-al. Most rögzített [4, 9] intervallum mellett k-t növeljük 1, 2 és 3-ra. Ezt kapjuk:

 

 

Ugyanazon intervallumok esetén az x0 mindig ugyanakkora, amely mindig nagyobb mint az m.

 

 

 

Ebben a részben a négyzetes közepet előállító függvényt ábrázoljuk. Ez függvény az f(x) = kx. Nézzük a szokásos képleteket:

 

 

Ezek után írjuk fel az I(p) függvényt.

 

 

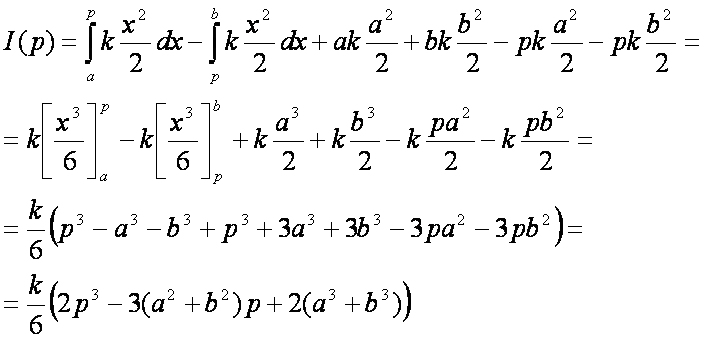
Írjuk fel az I(p) függvény deriváltját és határozzuk meg a zérus helyét.

 

 

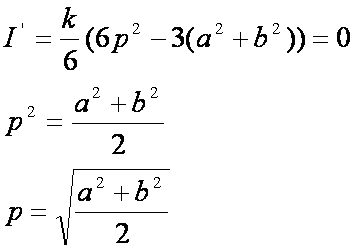
A grafikonok a következő paraméterekkel lettek megrajzolva: [1, 5] szakaszon k = 0,2 és [7, 12] szakaszon, ahol k = 0,1.

 

 

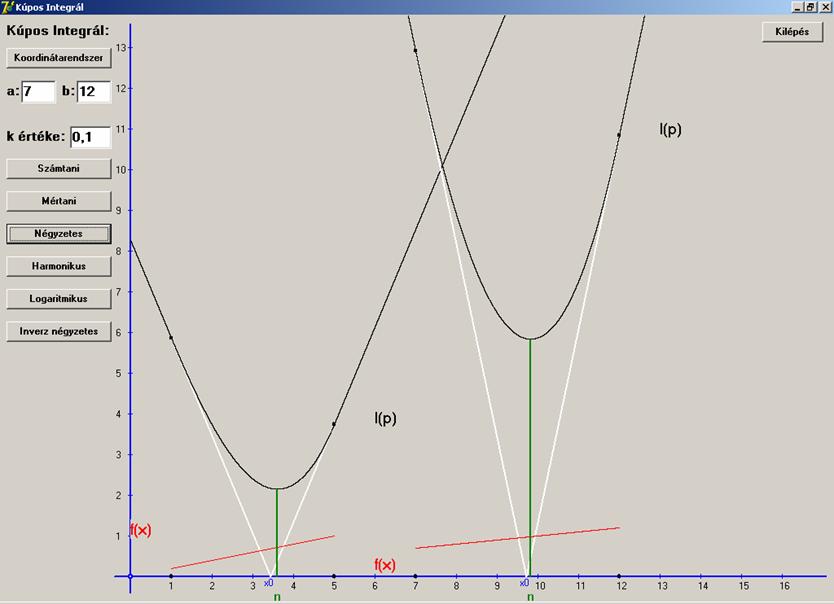
Látható, hogy most az x0 kisebb mint a p0, azaz kisebb a négyzetes középnél.

 

 

 

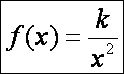
Ebben a részben a harmonikus középnek megfelelő függvény vizsgálata a cél. Ez a függvény az f(x) = k/x2 függvény lesz. Következzenek a szokásos képletek.

 

 

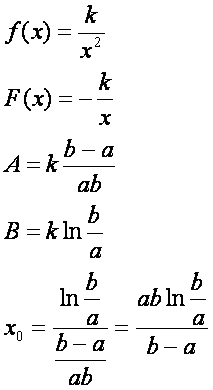
Ezek után írjuk fel az I(p) függvényt.

 

 

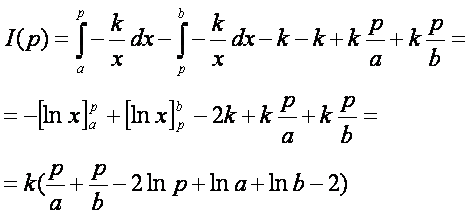
Nézzük a deriváltját és annak zérus helyét:

 

 

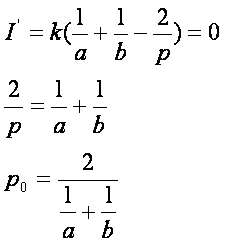
A minimum valóban a harmonikus középnél van. Ábrázoljuk a következő paraméterekkel a függvényünket: [3, 14]-es intervallumon k = 4 értékre.

 

 

A k értékét azért kellett relatív magasra választani, mert a függvényértékek aránylag kicsik, nagyon lapos lett volna a függvény egy 1 körüli k-ra. Látható, hogy az x0 most nagyobb, mint a harmonikus közép értéke.

 

 

 

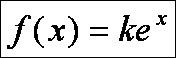
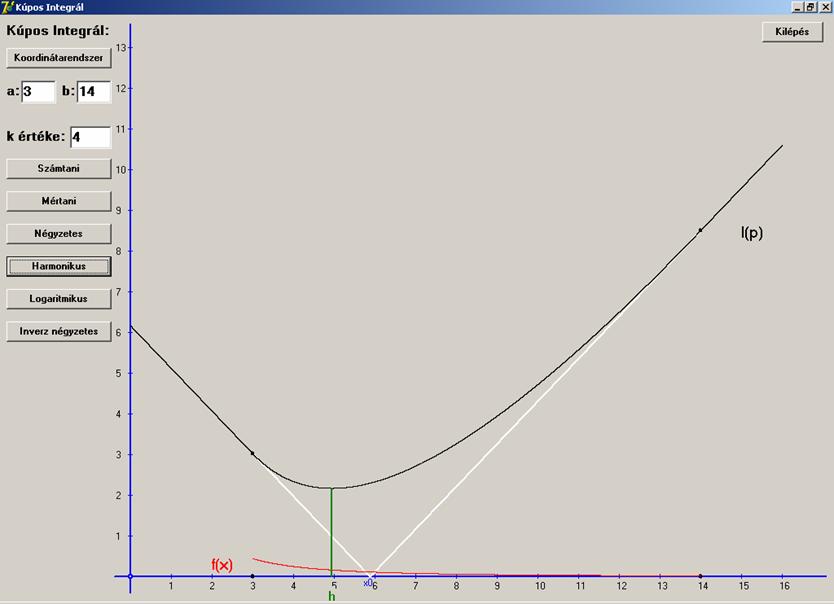
Nézünk egy példát nem szokványos középre. Ezt én logaritmikus középnek neveztem el. Generáló függvénye az f(x) = kex. Haladjunk a megszokott lépésekkel a cél felé.

 

 

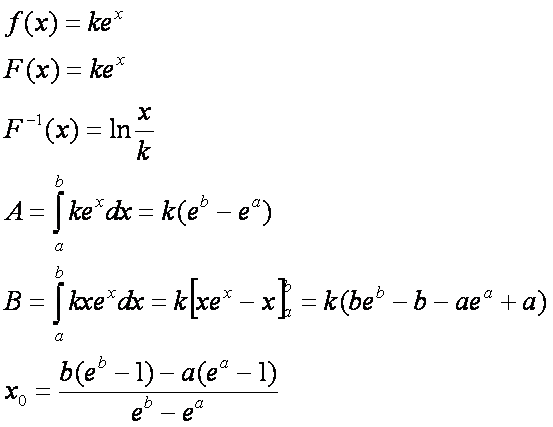
Ezek után írjuk fel az I(p) függvényt.

 

 

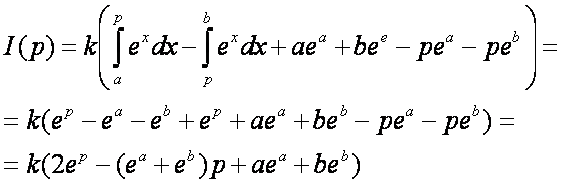
Vegyük az I(p) függvény deriváltját és határozzuk meg annak zérus helyét.

 

 

 

Az ábrázolás közben kiderült, hogy az aktuális I(p) függvény az előbbiekhez képest sokkal nagyobb értékeket vesz fel. Ez természetesen az exponenciális tagok miatt van így. Ezért kellett a k-t 0,005-nek választani. Az x0 most kisebb a p0-nál, azaz a logaritmikus középnél.

 

 

 

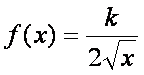
Nézzünk még egy nem szokványos közepet, mégpedig az inverz négyzetes közepet. Az elnevezés arra utal, hogy ez a négyzetes közép logikai fordítottja. Azaz, először vonunk gyököt a számokból, és végén emelünk négyzetre. De lássuk a most is a szokásos lépéseket.

 

 

Ezek után írjuk fel az I(p) függvényt.

 

 

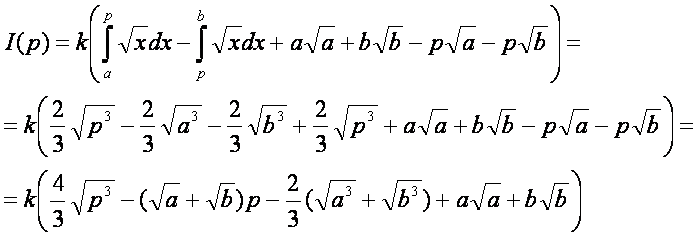
Vegyük az I(p) függvény deriváltját és határozzuk meg annak zérus helyét.

 

 

Nézzük ezek után az I(p) szokásos ábrázolásban.

 

 

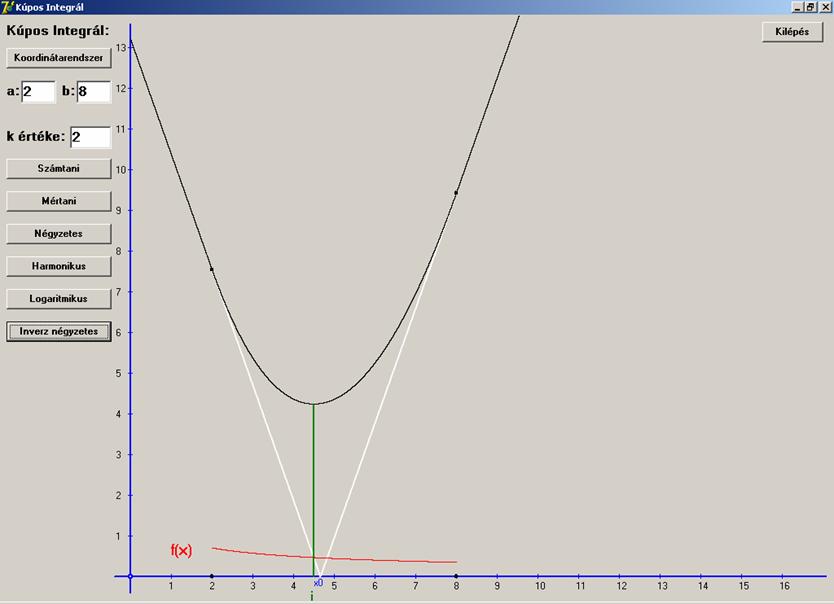
Az x0 most nagyobb a p0-nál, azaz az inverz négyzetes középnél.

 

Ábrázoltam egy képernyőn, ugyanazon intervallum felett mind a hat függvényt azért, hogy a közepek közötti nagyságrend megfigyelhető legyen. Egy kicsit sűrű lett az ábra. Ezért úgy döntöttem, hogy két részre bontom az ábrázolást. Elsőn a három kisebb közepet, a másodikon a három nagyobbat rajzoltatom le. Az intervallum legyen [2, 8]. A számtani közép értéke 5. Látható, hogy az első képernyőn minden közép kisebb ennél.

 

 

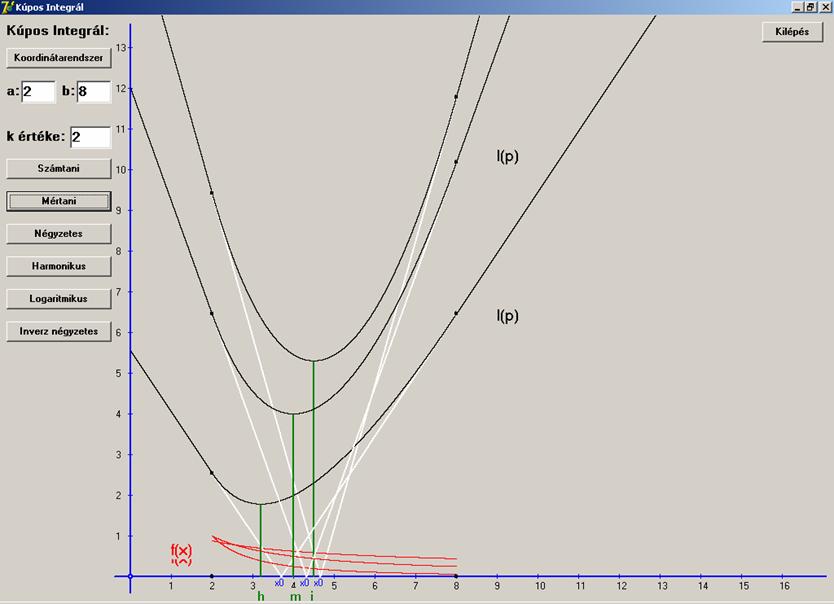
Az első ábrán a közepekhez tartozó k értékek:

 

harmonikus: k = 4,

mértani: k = 2,

inverz négyzetes: k = 2,5.

 

 

A másodikon a k értékek:

 

számtani: 0,4

négyzetes: 0,05

logaritmikus: 0,002.

 

Az, hogy melyik grafikon melyik középhez és generáló függvényhez tartozik, a h, m, i, s, n és l jelölés elárulja. Jól látszik a két képernyő alapján, hogy a közepek közötti nagysági sorrend:

 

 

Természetesen bármely kettő közötti nagyságrend algebrailag is igazolható. Nehezebben, de az x0 és a közepek közötti nagysági viszony is látható. Mindezt megkönnyítendő, íme a helyes relációk:

 

h < x0

m < x0

i < x0

x0 = s

x0 < n

x0 < l

 

Érdekességként megjegyezhetjük, hogy számtani közép középen van. Erre a középre az x0 a középpel egyenlő. A többi középre egyfajta fordított értelmű viszony áll fenn. A számtani középnél kisebb közepekre az x0 a nagyobb, míg a nagyobbakra a közepek nagyobbak x0-nál. Vizsgálódásunk végére értünk. Remélem hasznos információkkal ismertethettem meg olvasóimat.

 

Következő lap: http://gorbem.hu/MT/Izogonalis8.htm