Izogonális (6)

Gondolatok a legkisebb négyzetek módszeréről

Az első lapon (Izogonális (1)) említettem, hogy az alapfeladatnak számos átalakítása, kibővítése, kiterjesztése lehetséges. Említettem, hogy egy pont helyett kereshetnénk egyenest is, azaz:

A feladat: Adott a síkban n darab pont. Adjuk meg azt az egyenest ebben a síkban, amelytől az adott pontok távolságösszege minimális. (Ez is IMT, csak pont helyett most egyenest keresünk.)

Pontok és egyenesek egy síkon és valami minimális!? Ezek alapján eszünkbe juthat a valószínűség számításból jól ismert:

Gauss - Markov-tétel: Ha az x és y véletlen mennyiségek között lineáris kapcsolatot tételezünk fel, azaz egy y = a*x + b egyenessel közelítjük, akkor az a és b paramétereknek a legkisebb négyzetek módszerével kapott becslései az összes lineáris becslések között a legkisebb szórásúak.

A legkisebb négyzetek módszerénél az egyenes egyenletében található a és b értékét úgy választjuk meg, hogy a

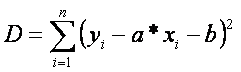
négyzetösszeg, a lehető legkisebb legyen. Egy konkrét feladattal kapcsolatban arra van szükség, hogy az a és b konstansokat meghatározzuk. Az D egyenletéből adódó Gauss-féle normálegyenletek a-ra és b-re lineáris egyenletrendszert adnak, melyek könnyen megoldhatók. Az eredmények a következők: Ha

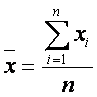és ,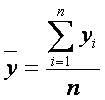

azaz a véletlen x és y mennyiségek átlagai, akkor az egyenes a és b paraméterét így kapjuk:

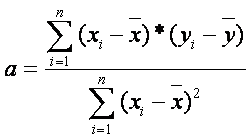
és

Jelen lapon azt vizsgálom, hogy ha a legkisebb négyzetek módszere helyett lineáris közelítést alkalmazunk (azaz nem az y szerinti eltérések négyzetével, hanem az egyenestől mért valódi távolságokkal számolunk), akkor ez milyen eltérést mutat, a közelítő egyenestől vett távolságösszeg minimalizálása tekintetében.

Térjünk át most a fentebbi feladathoz (keressünk IMT egyenest). Mivel a feladat megoldásában csak geometriai, koordináta-geometriai és analitikus fejtegetések találhatók, csak geometriai oldalról fogalmazzuk és oldjuk meg a feladatot.

A megoldás:

I. rész: Bebizonyítjuk, hogy ezen az egyenesen rajta van legalább egy az n pont közül.

Indirekt módon bizonyítunk.

A lenti ábra alapján: tegyük fel, hogy e a keresett egyenes és nincs rajta egyetlen pont sem. Ez pontosan azt jelenti, hogy e körül e₁ és e₂-vel kijelölhető egy 2d szélességű sáv, melyben nincs pont. Így az e egyenes a pontokat két részre osztja.

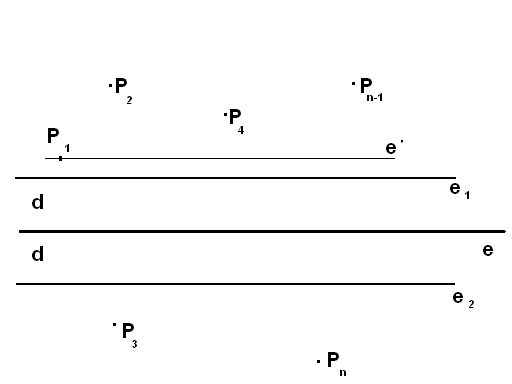
a) Ha az egyenes két oldalán ugyanannyi n/2 pont van (azaz n páros), akkor az e-vel párhuzamos és az említett sávban elhelyezkedő egyenesek vele azonosan jó tulajdonságúak sőt, ha P₁ van a legközelebb e-hez, akkor a P₁-en átmenő e-vel párhuzamos egyenes is e-vel azonosan jó tulajdonságú (e').

b) Ha a két részre szakadt pontok száma nem egyenlő, akkor, ha a P₁-el meghatározott oldalon van több, akkor e-nél minden, a P₁ oldalára eső, d sávban lévő, e-vel párhuzamos egyenes jobb tulajdonságú, mint az e (ha mozgatjuk a keresendő egyenest, akkor több ponthoz kerül közelebb, mint ahánytól távolodott). Nevezetesen, ha tekintjük a P₁-en (mint legközelebbi ponton) átmenő, e-vel párhuzamos egyenest, akkor ez, jobb tulajdonságú lesz, mint e.

Így e nem lehet a legjobb tulajdonságú egyenes, ugyanis van nála jobb (vagy vele azonosan jó) tulajdonságú, amelyre pont illeszkedik. Ezzel beláttuk, hogy az egyenesnek mindenképp át kell mennie egy ponton az adott n pont közül.

II. rész: Bebizonyítjuk, hogy ezen az egyenesen még egy további (azaz összesen legalább kettő) pont rajta van a megadott n pont közül.

Az egyenesek és pontok kölcsönös helyzete, távolsága független a koordináta reprezentációtól. Ezért K₀-ban legyenek a koordináták P_0i(a_i, b_i). Át fogunk térni minden pontban olyan koordinátarendszerre, melynek középpontja az illető pont és a tengelyek irány szerint párhuzamosak K₀ tengelyeivel. A pontok koordinátái a pontokhoz rögzített koordinátarendszerekben:

K₁-ben a P_i koordinátái P_1i(a_i-a₁, b_i-b₁),

K₂-ben a P_i koordinátái P_2i(a_i-a₂, b_i-b₂),

.

.

.

K_n-ben a P_i koordinátái P_ni(a_i-a_n, b_i-b_n), ahol i = 1,2, ... ,n.

Minden koordinátarendszerben a keresett minimális tulajdonságú egyenes egyenlete a következő alakban írható fel (mivel átmegy a lokális koordinátarendszer origóján, mint az egyik ponton az n közül):

mx - y = 0.

Az egyenletet normál alakja:

.

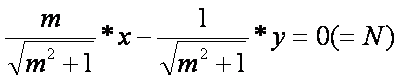Egy adott pont P(x₀, y₀) tőle vett távolsága:

,

ahol N(P) a pont koordinátáinak helyettesítési értéke.

Így a j. ponton (j<>i) átmenő egyenestől vett távolságösszeg:

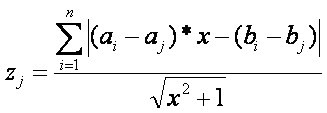
Ezek után az elvi megoldás: meghatározzuk minden j mellett a fenti függvény minimumát. (Itt lényegében n-1 db függvény minimumát kell kiszámítani, hiszen j nem lehet egyenlő i-vel.) Aztán az n-1 minimum érték közül ki kell választani a legkisebbet. Ez lenne a feladat megoldása, mármint az, hogy milyen i-re lesz a legkisebb, mert akkor az a pont lesz a másik pont, amin átmegy az egyenes. A fenti függvények szélsőértékének meghatározása az abszolút érték miatt (ha alakjukat nem változtatjuk meg) nem lehet analitikus. (deriválással nem lehet a szélső értéket meghatározni). Így nehezen járható ez az elvi megoldás.

Keressünk nem analitikus megoldást (persze analitikus eszközökkel).

Belátjuk, hogy a keresett szélsőérték szempontjából a függvény nevezője nem számít.

A fenti függvény szakaszonként a következő alakban írható fel:

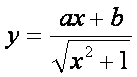
Vizsgáljuk tehát ez utóbbi függvényt. A függvény menetének vázolása érdekében képezzük az első deriváltját:

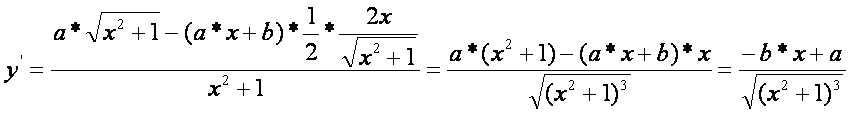
Ennek zérus-helye:

,

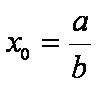ahol természetesen a b nem lehet nulla.

Az y függvény értéke a deriváltja zérus-helyénél:

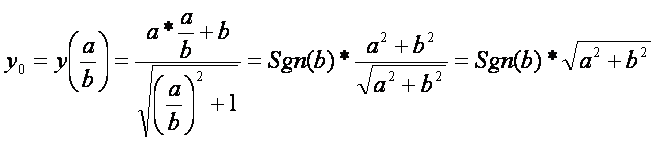
Ahol Sgn az előjelfüggvény.

Mivel a minimumhely környezetében a függvény első deriváltja előjelet vált (a számláló lineáris függvény, a nevező mindig pozitív), így a függvénynek (ha b<>0) szélsőértéke van. A szélsőérték jellegének és a függvény menetének megállapítása érdekében vegyük a függvény második deriváltját:

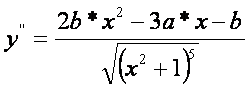
Ennek zérus-helyei:

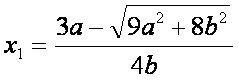
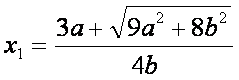
Az y függvény határértéke a végtelenben:

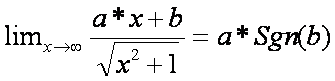
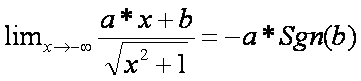
Vázoljuk a függvény lehetséges menetét. A fentiek alapján két eset lehetséges:

a) Ha b > 0, akkor az y függvény menete:

-∞	<	x1	<	x2	<	∞
	konvex	inflexió	konkáv	inflexió	konvex

Ekkor a szélsőérték csak maximum lehet. Mivel helyi maximum abszolút minimum nem lehet, ez az eset nem fordulhat elő, mivel minimumot keresünk (a konvexitás alulról értendő).

b) Ha b < 0, akkor az y függvény menete:

-∞	<	x1	<	x2	<	∞
	konkáv	inflexió	konvex	Inflexió	konkáv

Ekkor a szélsőérték csak minimum lehet. Ebben az esetben a felvett minimális érték:

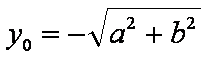
azaz negatív. Mivel a z_j bármely j-re bármely intervallumon nem negatív, így ez az eset sem fordulhat elő. Azért, hogy a függvény elemzését szemléltessük és leellenőrizzük, ábrázoljuk a függvényt a következő konkrét érékekre:

1) a = 3, b = 2 (A koordináta rendszerben fekete színű grafikon.)

2) a = 3, b = -2 (A koordináta rendszerben kék színű grafikon.)

3) a = -3, b = 2 (A koordináta rendszerben lila színű grafikon.)

4) a = -3, b = -2 (A koordináta rendszerben szürke színű grafikon.)

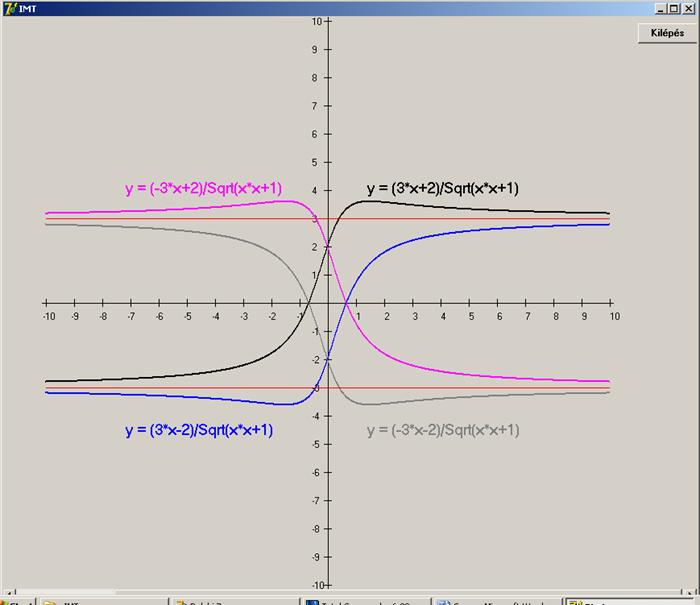
Az a és b együttható egyéb megválasztása esetén sem kapunk ezektől különböző menetű függvényeket. Látható, hogy b>0 esetén a függvénynek valóban maximuma, b<0 esetén pedig minimuma van (ami viszont negatív érték). Mint már korábban említettem b=0 nem lehet, mert ekkor sincs szélső érték (nevező nem lehet nulla). Mivel b minden lehetséges esetét végignéztük, azt a következtetést vonhatjuk le, hogy a z_j függvényeknek egyetlen differenciálható pontjában sem lehet a feladatnak megfelelő szélső értéke. Ezek a függvények tehát csak töréspontjaiban vehetnek fel minimumot. Ez pontosan azt jelenti, hogy a j. pont mellett még egy ponton átmegy a legjobb tulajdonságú egyenes.

Ezek után az egyenes meghatározásának menete:

Adottak tehát K₀-ban a P_0i(a_i, b_i) koordináták.

Képezzük:

K₁-ben a P_1i(a_i-a₁, b_i-b₁),

K₂-ben a P_2i(a_i-a₂, b_i-b₂),

...

K_n-ben a P_ni(a_i-a_n, b_i-b_n) koordinátákat.

Felírjuk a rendezett:

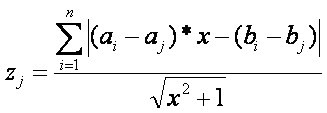
függvényeket és képezzük belőle a következőket:

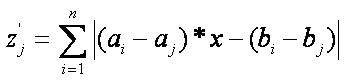
Állítsuk elő ez utóbbi függvények meredekség-sorozatait:

m₁₁, m₁₂, ... ,m_1n+1

m₂₁, m₂₂, ... ,m_2n+1

...

m_n1, m_n2, ... ,m_nn+1.

Minden meredekség-sorozat monoton növekvő, hiszen az abszolút értékes függvények tagjait pozitív előjellel adjuk össze.

Keressük meg a meredekség sorozatokban az előjelváltásokat. Ezekben a töréspontokban behelyettesítjük az x₀ = (a_i-a_j)/(b_i-b_j) értékeket és a kapott értéket

értékkel normáljuk. Az így kapott n szám közül ki kell választani a legkisebb értékeket (ez legalább két érték és hely lesz). A két hely (melyet a j határoz meg) jelenti azt a két pontot, amelyeken átmenő egyenest kerestük. Ha a minimális értékek száma több mint kettő, akkor a feladatnak több megoldása van.

Ellenőrzés és demonstráció végett a probléma vizsgálatára számítógépes program is készült. A próbafuttatások eredményei azt mutatják, hogy minél függvényszerűbb kapcsolat áll fenn a pontok koordinátái között, a lineáris illesztés és a legkisebb négyzetek módszere alapján történő illesztés annál kisebb eltérést mutat, egymáshoz képest. Mindemellett a lineáris illesztésnél a távolságösszeg mindig kisebb, mint a Gauss illesztésnél. 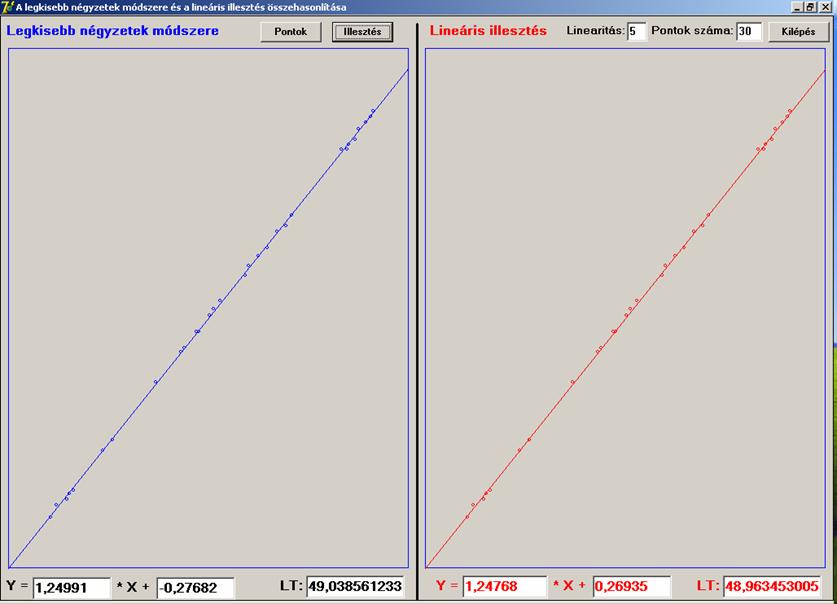Pontosabban minden olyan esetben, amikor a mérési eredmények között nincs funkcionális kapcsolat (azaz jelen esetben a pontok nem esnek egy egyenesre), a lineáris közelítés ad jobb - azaz kisebb - minimál-összeget. Nézzünk erre néhány futtatási képet. A megjelenítés igen egyértelmű. Bal oldalt a Gauss, jobb oldalt a Lineáris illesztés látható. Alul láthatjuk az illesztő egyenesek egyenletét, és a lineáris távolságösszegeket (LT).

Legyen a pontok száma 30.

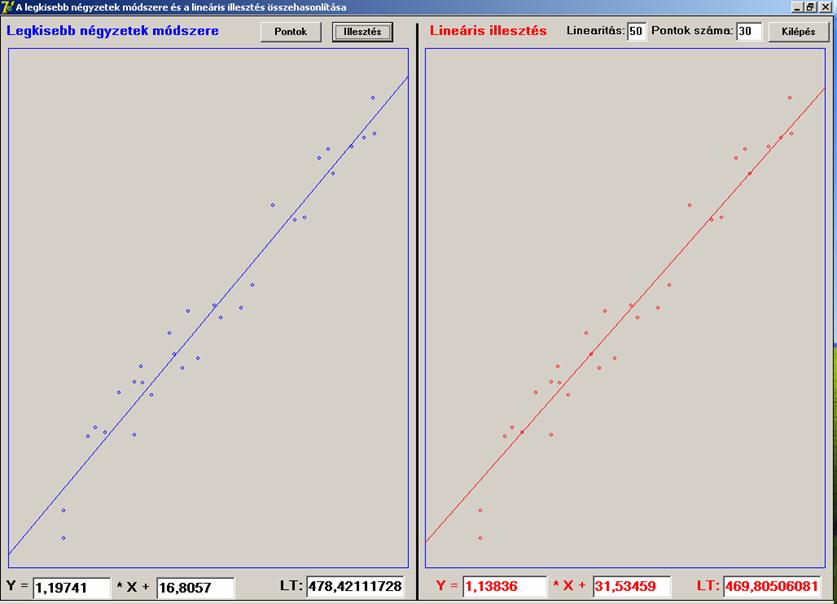
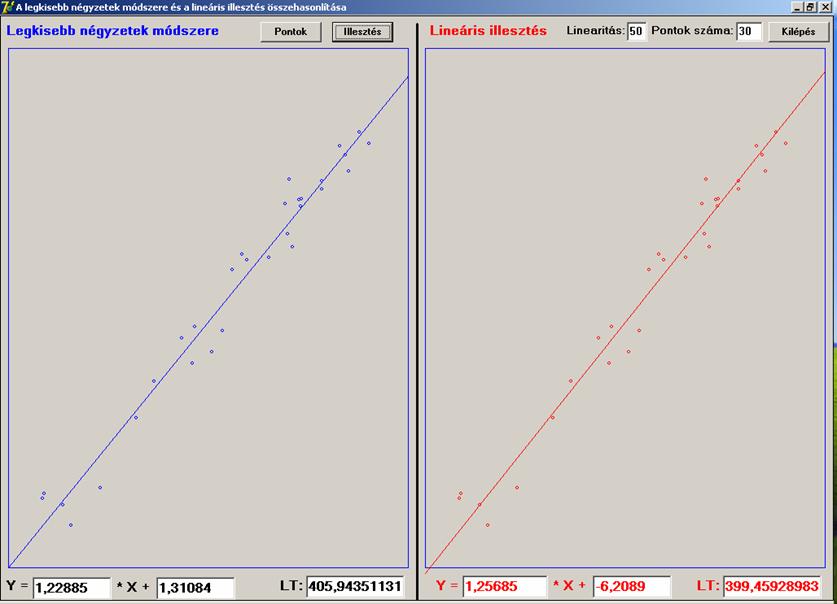
Mindkét esetben az eltérés 2% körüli a lineáris illesztés javára. Nézzünk egy 40 pontos esetet:

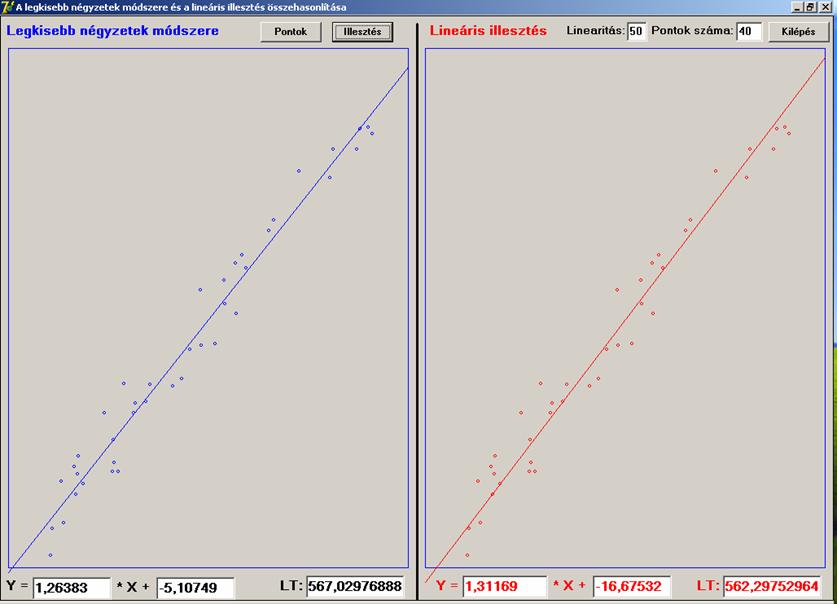
Itt az eltérés kisebb, mint 1%, szintén a lineáris közelítés javára. Javítsunk a linearitás mértékén, amellyel a pontoknak az egyenestől való eltérését csökkenthetjük:

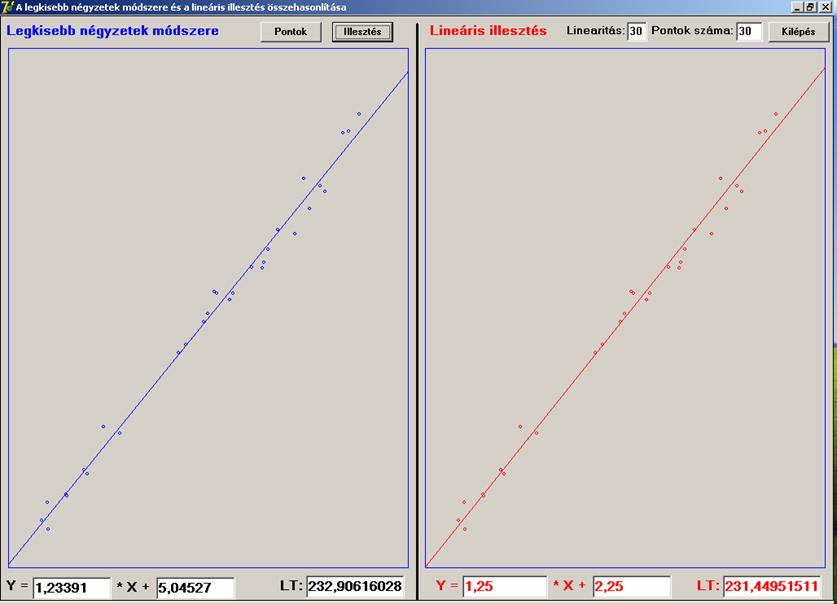
Az eltérés kisebb, mint fél százalék. Tovább csökkentve:

Az eltérés egyre kisebb. Ha a pontok számát csökkentjük, hasonlóan csökken a különbség:

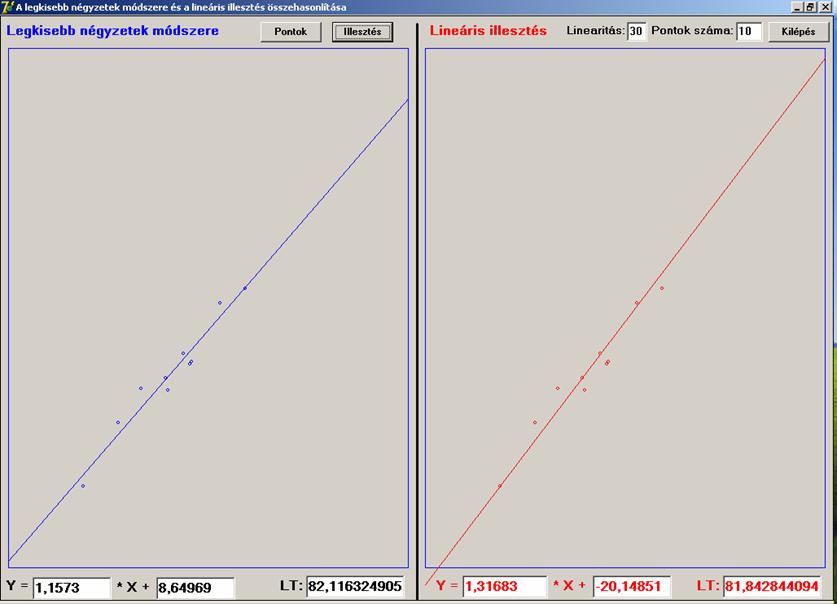
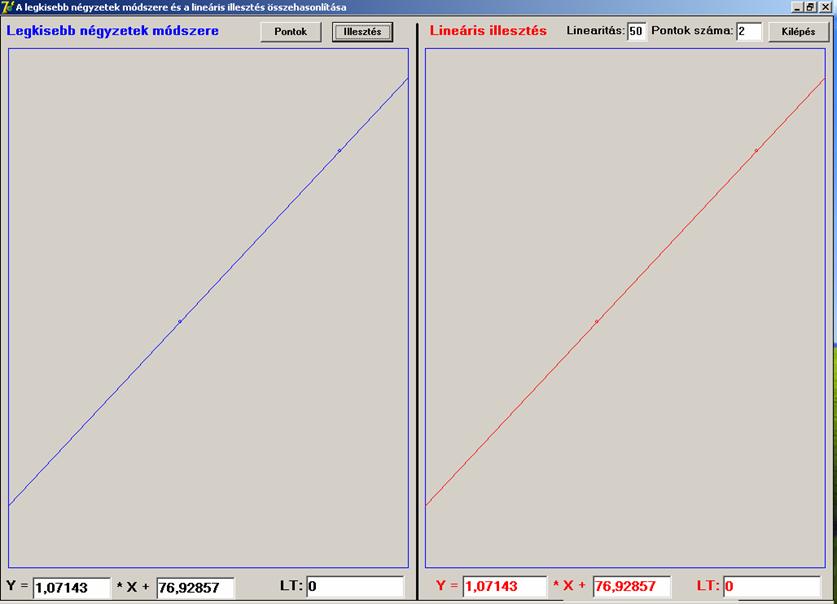
Természetesen 2 pont esete már funkcionális kapcsolatot jelent (egy egyenesen van), itt minkét közelítés 0 eltérést mutat.

Következő lap: http://gorbem.hu/MT/Izogonalis7.htm