Háromszögek (5)

Vissza: http://gorbem.hu/Matematika.php

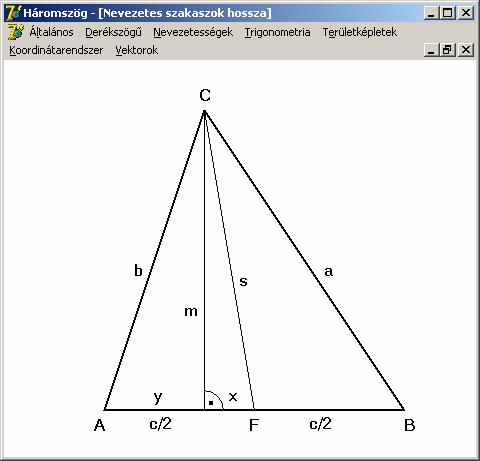
A háromszög nevezetes szakaszainak hossza

A magasságok hossza

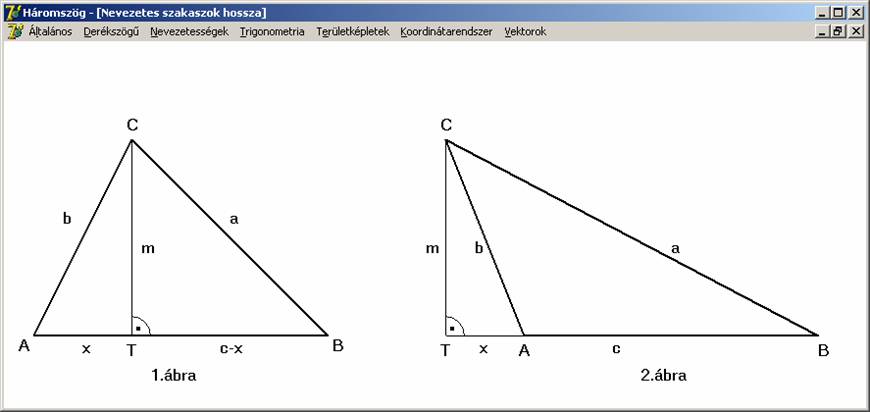
Használjuk az előző rajz 1. ábrájának jelöléseit és alkalmazzuk a Pitagorasz tételt:

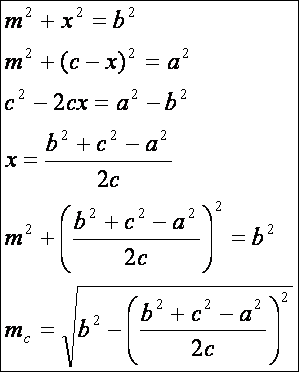
Vajon mi a helyzet tompaszögű háromszög esetén, amikor a T magasságtalppont nem esik a c oldalra (mint a fentebbi rajz 2. ábráján), csak annak meghosszabbítására:

Látható, hogy az eredmény ugyanaz. Hasonlóan a további két magasság:

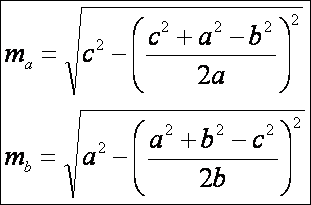
Vizsgáljuk meg egy kicsit a kapott képleteket (ténylegesen nyilván elég egyet). Az m_c képletében az a és a b szerepe nem látszik ugyanannak, mintha nem lenne mindegy, hogy milyen az oldalak sorrendje. Járjunk ennek utána, cseréljük fel a szerepüket, lássuk mit kapunk:

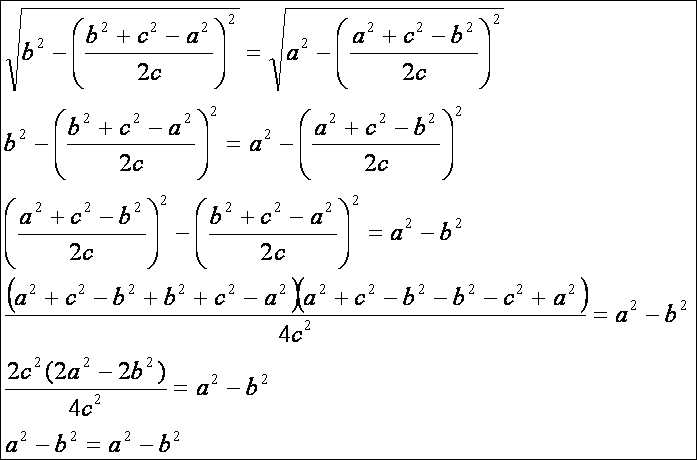
A cserével kapott képlet ugyanazt az értéket adja, mint a csere előtti. Vajon a képletben a négyzetgyök alatt mindig pozitív érték található (nulla nem lehet, mert akkor nincs háromszög)? A válasz:

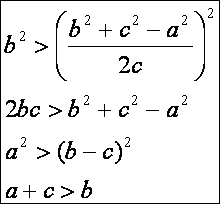
Ez a feltétel a háromszög-egyenlőtlenségre vezetett, tehát a válasz igen. Még az előző lapon (Haromszog3.htm) mutattuk meg, hogy a magasságok hossza a hozzájuk tartozó oldalak hosszával fordítottan arányosak. Ezt valóban ezek a képletek is teljesítik:

Semmi kétség afelől, hogy a képletek a helyes eredményt szolgáltatják. De nézzük még meg a háromszögek speciális eseteire is, hogy mit kapunk. Egyenlő oldalú háromszög: a = b = c:

Ez rendben van. Egyenlő szárú háromszög esetén a = b:

Ez is helyes. Legyen a háromszög derékszögű a² + b² = c²:

Tehát minden rendben, a képletek a speciális háromszögekre is alkalmazhatók. Ha már van képletünk a magasságra az oldalak segítségével, akkor van a területre is. Vajon ez elvezet a Heron képlethez?

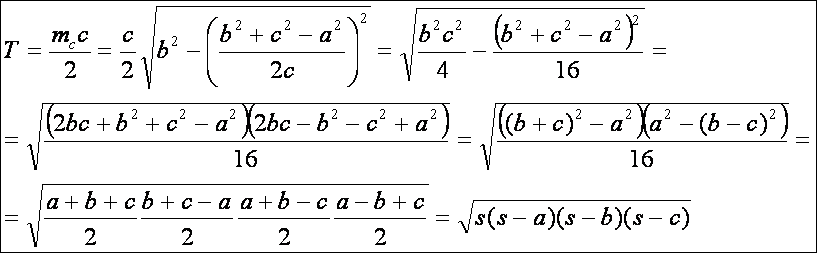
Természetesen igen, a Heron képletet kaptuk.

A szögfelezők hossza

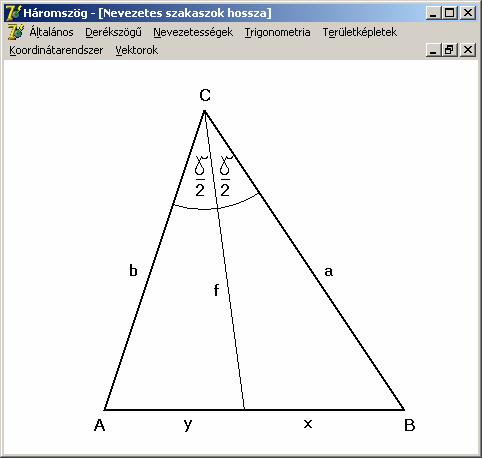
Tudjuk, hogy a szögfelező a szemközti oldalt a szomszédos oldalak arányában osztja. Használjuk ezt fel és alkalmazzuk a fenti rajz jelöléseit, valamint a koszinusz tételt:

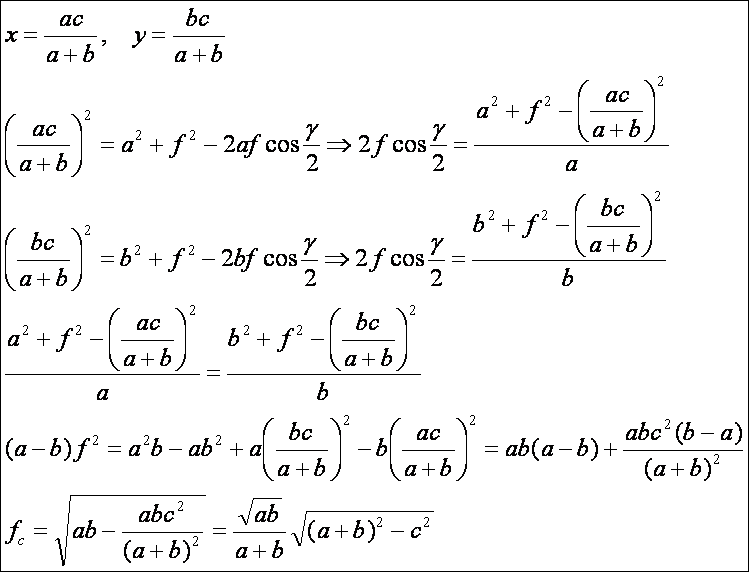
Hasonlóan a további szögfelezők:

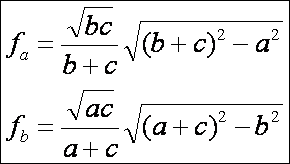
A szögfelezők képletében az oldalak jól látható módon szimmetrikusan szerepelnek, így itt ebben a témában nem kell vizsgálódni (például az f_c-ben az a és b helyzete szimmetrikus). Lássuk azt az esetet, amikor a háromszög szabályos, azaz a = b = c:

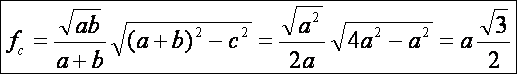
Helyes az eredmény. Nézzük azt az esetet, amikor a háromszög egyenlőszárú, azaz a = b:

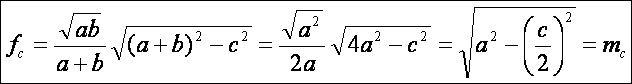
Most is minden rendben, a szögfelező a háromszög szárszögét felezi, merőleges az alapra, azaz egyúttal az alaphoz tartozó magasság is.

A súlyvonalak hossza

Használjuk az előző rajz jelöléseit és a már kiszámolt m magasságot, valamit alkalmazzuk a Pitagorasz tételt:

Hasonlóan a többi súlyvonal:

Az oldalak szimmetrikus szerepe nyilvánvaló, tehát ebben a témában nem kell vizsgálódni. Nézzük meg itt is a speciális háromszögeket. Kezdjük a szabályossal, azaz a = b = c:

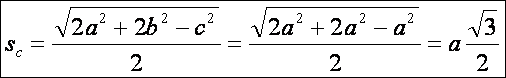
Ez rendben. Nézzük az egyenlő szárú esetet, azaz a = b:

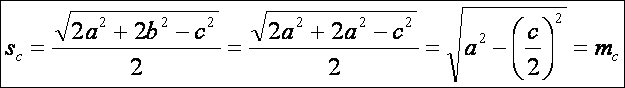
Ez is rendben. Következik a derékszögű háromszög, azaz a² + b² = c²:

Ezzel sincs semmi probléma, a derékszögű háromszögben az átfogóhoz tartozó súlyvonal a köré írható kör középpontjába vezet, így a hossza a kör sugarával, c/2-vel egyenlő.

A „KiSFiaM” tétel

Az Euler-egyenes

Az ABC háromszög köré írható kör K középpontja, az S súlypontja és az M magasságpontja (ilyen sorrendben) egy egyenesre illeszkednek, melynek neve Euler-egyenes. Az S a KM szakasz K-hoz közelebbi harmadoló pontja. Ezért a beszédes KiSFiaM elnevezés, mert a magánhangzók száma a KM szakaszainak arányát kifejezi valamint az F is a szó közepén található – mint a szakasz felezőpontja – amelynek a következő tételben még fontos szerepe lesz.

A bizonyításhoz tekintsük a következő rajz 1. ábráját. Ezek alapján a következő azonosítások érvényesek (a K’ a K pontnak az AB oldalra vonatkozó tükörképe, és a vektort aláhúzással jelöltük):

Azaz a K pontot tekintjük a sík origójának. Ekkor a súlypontba mutató helyvektor:

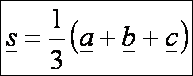
Azt kell belátnunk, hogy az m = 3s vektor valóban a magasságpontba mutat, mint ahogy azt az ábrán rajzoltuk. Tekintsük a következőt:

Vegyük a következő skaláris szorzatot (az aláhúzás nélküli betű a vele azonos nevű vektor hosszát jelöli):

Mivel a=b=c=r (mindegyik vektor hossza egyenlő a háromszög köré írható kör sugarával) így az előbbi skaláris szorzat nulla. Ami azt jelenti, hogy a CM szakasz merőleges az AB oldalra, vagyis a CM az AB oldalhoz tartozó magasságvonalon helyezkedik el. Hasonlóan a másik három oldalra vonatkozóan ugyanezt beláthatnánk, azaz az M valóban a háromszög magasságpontja. Ezzel azt is beláttuk, hogy a KM szakasznak a harmadoló pontjában a háromszög S súlypontja, hiszen az s vektor az m vektornak a harmada (ezzel azt is állítjuk, hogy a K-ból a csúcsokba mutató vektorok összege az M pontba mutat).

Megjegyzés (1): mivel az a, b és c vektor hossza azonos, az ábra szerinti AK’BK négyszög rombusz. Ezért az átlóira illeszkedő a + b és b – a vektorok nyilván merőlegesek egymásra. (Másképpen fogalmazva: két azonos nagyságú vektor összege és különbsége merőleges egymásra).

Megjegyzés (2): természetesen szabályos háromszög esetén egyértelmű Euler-egyenes és KM szakasz sem létezik, mert ekkor a K, S és M pontok egybeesnek.

A Feuerbach-kör

A KM szakasz F felezőpontja egy olyan körnek a középpontja, amely átmegy a három oldalfelező ponton, a három magasság talpponton és a magasságpontot a csúcsokkal összekötő szakaszok felezőpontján. Ezért ezt a kört szokás a kilenc pont körének, vagy Feuerbach körnek nevezni. A Feuerbach kör sugara, a háromszög köré írt kör sugarának a fele. Ennek a két körnek a hasonlósági középpontja a háromszög M magasságpontja.

A bizonyításhoz használjuk a fentebbi rajz 2. ábráját és a következő azonosításokat:

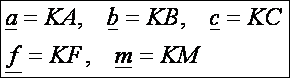
Azaz itt is a K pontot tekintjük a sík origójának. Legyen továbbá F_a, F_b és F_c az oldalak felezőpontja. T_a, T_b és T_c a magasságok talppontjai. M_a, M_b és M_c a magasságpont és a csúcsokat összekötő szakaszok felezőpontjai. F a KM szakasz felezőpontja, T pedig T_cF_c felezőpontja, továbbá R a háromszög köré írható kör sugara.

Ekkor igazak a következők:

(Egyébként az FM_c szakasz a KCM háromszög KC oldalával párhuzamos középvonala.)

Az MKF_cT_c egy derékszögű trapéz, melynek az FT szakasz a középvonala. Így az FTT_c és az FTK_c derékszögű háromszögek egybevágóak, átfogóik egyenlő hosszúak, azaz:

Ezáltal a C csúcshoz kapcsolódó T_c, F_c és M_c pontok ugyanolyan, R/2 távolságra vannak az F ponttól, azaz egy körön helyezkednek el. Ugyanígy belátható az A és B csúcsokhoz tartozó (T_a,F_a,M_a, és T_b,F_b,M_b) pontokról is, hogy ugyanezen a körön vannak. Mindebből az is következik, hogy az M pontnak az M_a pont vonatkozó tükörképe A, az M_b pontra vonatkozó tükörképe B és az M_c pontra vonatkozó tükörképe C. Azaz a Feuerbach-körnek az M középpontú kétszeres nagyítása a háromszög köré írható kör, ahogy a tétel is állítja.

Megjegyzés (1): Szabályos háromszög esetén is létezik Feuerbach-kör, csak ekkor egybeesik a beírt körrel, középpontja a háromszög középpontja lesz. A kilenc pontból pedig az oldalfelező pontok és a magasságtalppontok egybeesnek, így csak hat pont köréről beszélhetünk.

Megjegyzés (2):A beír kör és a hozzáírt körök érintik a háromszög Feuerbach körét. Az Euler egyenes akkor és csak akkor megy át a háromszög valamelyik csúcsán, ha a háromszög egyenlő szárú és ekkor az Euler egyenes a háromszög szimmetriatengelye lesz. Ebben az esetben a háromszög Izogonális pontja is az Euler egyenesre esik.

A KM szakasz hossza

A fenti megjegyzésekből kiderült, hogy szabályos háromszög esetén a KM szakasz nem létezik, vagy másképpen a hossza nulla. De milyen hosszú akkor, ha a háromszög nem szabályos. A feladat: fejezzük ki a KM szakasz hosszát a háromszög oldalaival.

Megoldás: mivel a fentebbi tételek bizonyításánál használt a, b és c vektorok (ezen az ábrán a szerepüket az x, y és z vektorok veszik át) hossza r, a köré írható kör sugara, ezért elsőnek ennek hosszát adjuk meg az oldalak segítségével. Tekintsük a következő ábrát:

Válasszuk ki a háromszögnek az egyik hegyesszögét (ilyen biztosan van), legyen ez a B csúcsnál. Rajzoljuk meg a háromszög C csúcsából induló magasságát, melynek talppontja a c oldalon legyen T_c. Húzzuk meg a háromszög köré írható körének a C -ből induló átmérőjét. Az AC’C szög és az ABC szögek kerületi szögek, ezért egyenlők. Ezáltal az AC’C és T_cBC derékszögű háromszögek hasonlóak. Ezért:

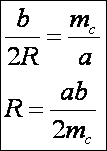
Ugyanakkor a háromszög területképletéből:

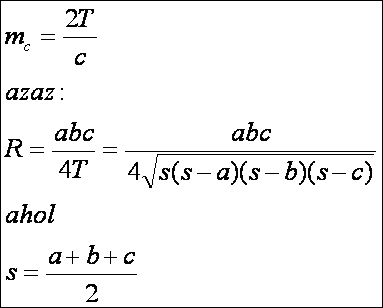
Ezek után nézzük a KM szakasz hosszát. Jelölje rendre az α, β és γ az y-z, z-x és x-y vektor-párok szögét, a rajz szerint. A fentebbi bizonyítások alapján:

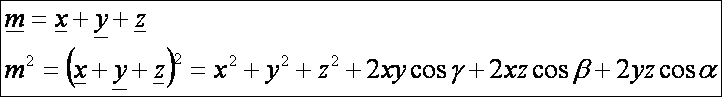
De az oldalakkal és a csúcsokba húzott sugarakkal alkotott háromszögekre a következő koszinusz tételek igazak:

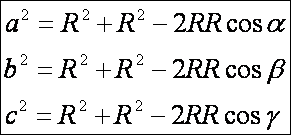
Ezekből a szögek koszinusza:

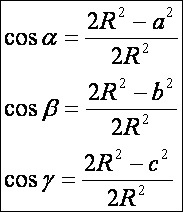
Helyettesítsük ezeket az m² képletébe és vegyük figyelembe, hogy x = y = z = r:

ahol s a félkerület. Ezzel a KM = m szakaszt kifejeztük az oldalak segítségével.

A KM szakasz hossza speciális háromszögekre

Szabályos háromszög esetén a KM hossza nulla, a kilenc pontból egybeesések miatt csak hat lesz, és minden, a K középponton átmenő egyenes a háromszög Euler egyenesének számít (vagy úgy is felfoghatjuk, hogy nem létezik). Nézzük, hogyan kapjuk a KM hosszát az egyenlő oldalú háromszög esetén, a fenti képlet alapján (a = b = c):

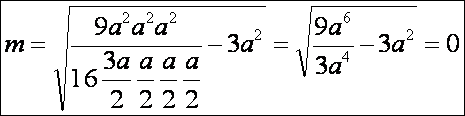
Derékszögű háromszögben M a derékszögű csúcs, K pedig az átfogó felezőpontja. Így a KM szakasz az átfogóhoz tartozó súlyvonal, melynek S a harmadoló pontja (mint súlyvonal-súlypont tulajdonság). A KM szakasz hossza derékszögű háromszögben R = c/2 = s_c. Ekkor a Feuerbach kör és a köré írható kör a derékszögű csúcsban érintik egymást és jól látható módon sugaruk aránya 1:2. Nézzük meg tehát, mit kapunk m-re derékszögű háromszögben (a² + b² = c²) a fenti képlet szerint:

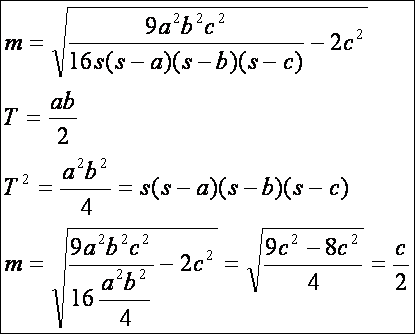
Végül mekkora m az egyenlő szárú háromszög esetén (a = b):

A K és M pont egyszerre van a háromszög belsejében (hegyesszögű háromszög), a háromszög kerületén (derékszögű háromszög) és háromszögön kívül (tompaszögű háromszög).

További nevezetes tételek háromszögekre

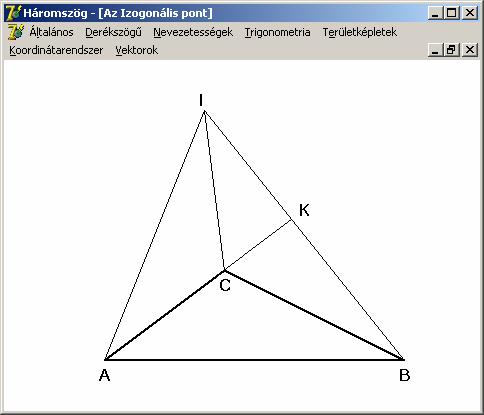
Az Izogonális pont.

Ha egy háromszögnek nincs 120º-os vagy annál nagyobb szöge, akkor azt a pontot, amelyből az oldalak ugyanazon, azaz 120º-os alatt látszanak, a háromszög Izogonális pontjának nevezzük.

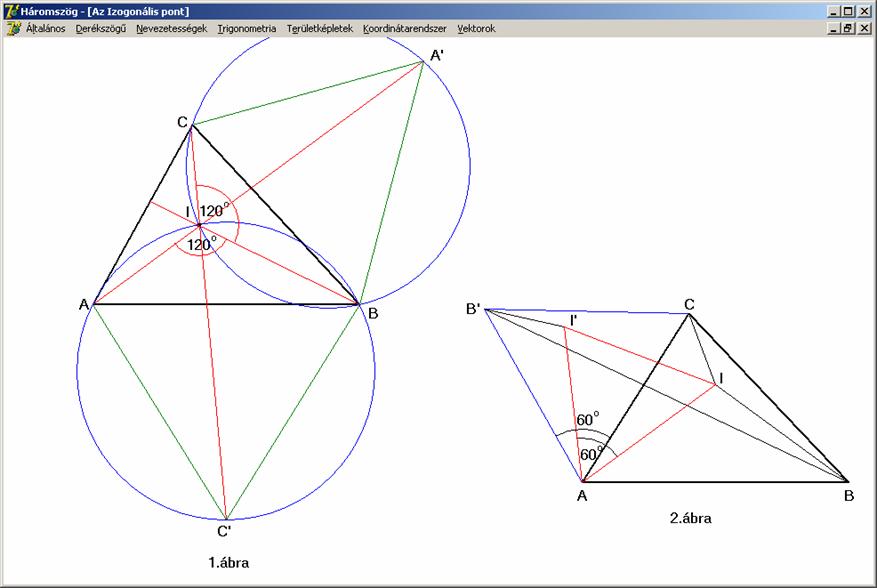
Az előző rajz 1. ábráján kétféle módot is láthatunk az Izogonális pont megszerkesztésére. Illesszünk a háromszög oldalaira kifelé szabályos háromszögeket, kapjuk a BC és AB esetén az A’ és C’ csúcsokat. Kössük össze az A-t az A’-vel, C-t a C’-vel. Mivel a háromszögnek minden szöge kisebb, mint 120º, ezért egyetlen csúcsnál sem jöhet létre egyenes-, vagy konkávszög. Ezért ezek a szakaszok az AC’BA’C konvex ötszög belsejében haladnak, mint átlók és metszik egymást, legyen ez a metszéspont az I. Nyilvánvaló, hogy az ABA’ és C’BC háromszögek egybevágók, hiszen a C’BC háromszög az ABA’ háromszögnek az óra járásával ellentétes irányú 60º-os elforgatottja a B pont körül (mellesleg így AA’ = BB’ = CC’). Az elforgatás miatt a BA’I szög a BCI szöggel megegyezik, így a BA’CI egy húrnégyszög, melynek az A’-nél lévő szöge 60º. Mivel a húrnégyszög szemközti szögeinek összege 180º, így a BIC szög 120º-os. Mindezt másik két oldalra megismételve adódik, hogy az I pont valóban az Izogonális. A 120º-os szög keletkezését a 60º-os elforgatás is bizonyítja, hiszen emiatt, ha mindhárom oldalon végrehajtjuk a szabályos háromszögek szerkesztését és a szemközti csúccsal való összekötést, akkor az I pont 6 darab 60º-os szög közös csúcsa. Ezek közül 2-2 együtt a háromszög oldalainak látószöge, amely így 120º-os. Az első szerkesztési lehetőség tehát: rajzoljunk az oldalakra kifelé szabályos háromszögeket, az újonnan keletkezett pontokat a szemközti csúcsokkal összekötve, a metszéspontok adják az Izogonális pontot. A másik lehetőség az, hogy szerkesszük meg az oldalak 120º-os látószöghöz tartozó köríveit (ezek teljes körei kék színűek az ábrán), melyek közös metszéspontja az Izogonális pont.

Tekintsük a következő feladatot: Adott a síkban n darab pont. Keresendő az a pont, amelyből az adott pontokba húzott szakaszok hosszának az összege – a sík bármely pontjára nézve – a lehető legkisebb. A háromszögek kapcsán ennek a feladatnak az n = 3 esete érdekes, ebből is csak az, amikor a három pont nem kollineáris. A feladat ekkor is két részre bontandó: van a három pont által alkotott háromszögnek 120º-nál nagyobb-egyenlő szöge, vagy nincs.

1. Lássunk egy meoldást arra az estre, ha a legnagyobb szög kisebb, mint 120º. Legyen tehát az ABC háromszög ilyen, ahogy azt a fentebbi rajz 2. ábráján is láthatjuk. Vegyünk fel a háromszög belsejében egy I pontot. Az A csúcs körül, az óra járásával ellentétes irányban, 60º-al forgassuk el az AIC háromszöget. Így kapjuk az AI’B’ háromszöget. A 60º -os elforgatás miatt az AII’ és az ACB’ háromszög szabályos, így AI’ és II’ szakaszok egyenlők. A BII’B’ törött vonal olyan hosszú szakaszokból áll, mint az I és a csúcsok közötti szakaszok. Ez a törött vonal a B és B’ pontokat köti össze, ami akkor a legrövidebb, ha egyenes. Azaz I-nek rajta kell lenni a BB’ szakaszon. Ha az I rajta van a BB’ szakaszon, akkor amiatt, hogy az AII’ szög 60º, a BIA szög (a háromszög külső szöge) 120º. Hasonlóan a további két oldalra mindezt végrehajtva adódik, hogy az I az Izogonális pont. Egyúttal azt is beláttuk, hogy az I -ből a csúcsokba húzott szakaszok összege a minimális és ez a minimális érték a BB’ szakasz hossza, amely mindhárom oldalra nézve ugyanaz: AA’ = BB’ = CC’.

Próbálkozzunk meg egy analitikus megoldással is. Vegyük fel a három pontot koordinátarendszerben úgy, hogy minden szöge kisebb legyen 120º -nál. Ilyet látunk a következő rajzon.

Jelölje D az IA, IB és IC szakaszok összegét. Ez analitikusan így állítható elő:

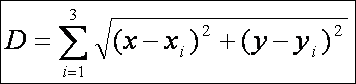
Ennek a kétváltozós függvénynek a minimumát kellene megkeresni. Közismert módszer erre a parciális deriválás, majd ezek zérus-helyeinek meghatározása, melyek a szélső értékek szükséges feltételeit adják. Íme a két parciális derivált.

Vegyük észre, hogy a törtek nevezőjében mindig az I és a pont távolsága van. Az első egyenlet számlálóiban x koordináta szerinti különbség, a másodikban az y koordináta szerinti különbség található, így ez szögfüggvényre enged következtetni. Valóban az I -hez rögzített lokális koordinátarendszerben az e egységvektor irányszögének koszinusza és szinusza szerepel a két fenti egyenletben. Írjuk fel ezeket:

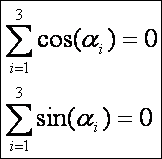
Nyilvánvaló, hogy ezek a szögfüggvény értékek nem lehetnek azonos előjelűek, hiszen akkor nem lehetne az összegük 0. Legyen a harmadik szög szinusza és koszinusza is negatív (mint például a rajzon). Így négyzetre emeléssel hamis gyök nem léphet fel. Rendezés és négyzetre emelés után ezeket kapjuk:

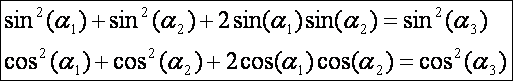
Az egyenleteket összeadva és rendezve:

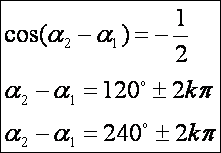
Azaz olyan összefüggéseket kaptunk, amelyből kiolvasható, hogy az I -ből a csúcsokba vezető szakaszok-os szöget zárnak be. Számolásunk eredménye nem konkrét szögérték, hanem csak a különbségekre ad feltételt. (Konkrét értékeket nem is várhattuk volna, hiszen ha a háromszöget például az I körül elforgatjuk, akkor ugyanaz a háromszög marad, de minden irányszög ugyanannyival megváltozik.) Ha az egyenleteket másképpen rendezzük (másik szög szögfüggvényértékeit tekintjük negatívnak), akkor hasonló eredményeket kapunk a további szögek különbségeire is.

Egy másik analitikus lehetőség a I meghatározására a Lagrange-féle multiplikátor módszer. Használjuk a következő ábra jelöléseit:

Ekkor a minimalizálandó függvény

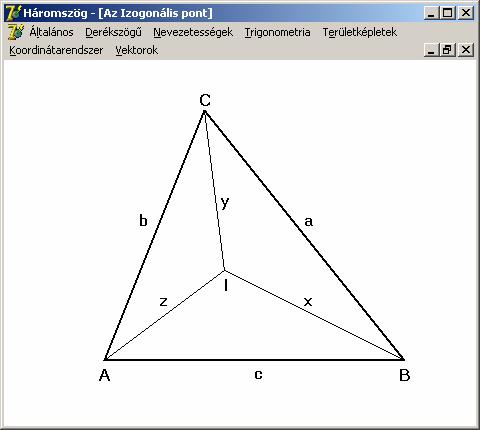
A feltételeket a koszinusz tételek szolgáltatják:

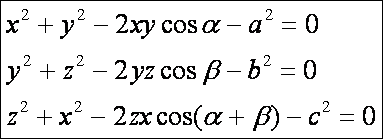
Az egyenletekben az I pontnál lévő szögek a koszinusz tételnek megfelelőek, és a harmadikban kihasználtuk, a koszinusz függvény tulajdonságát. Ezek után lássuk a D függvény leírását a Lagrange-féle módszer szerint:

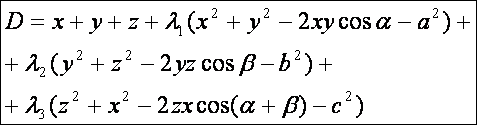
Vegyük a szükséges parciális deriváltakat, melyeknek nullának kell lenni a szükséges feltételhez:

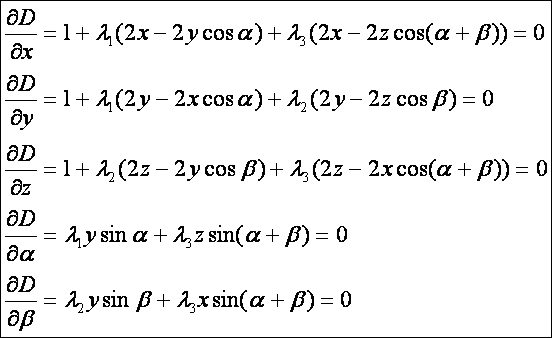
Ezzel egy 8 ismeretlenes () egyenletrendszert kaptunk, amelyet legalább a szögekre meg kellene oldani. A szükséges egyenletszám megvan, három a koszinusz tételből, öt a deriváltakból. A szögek szerinti deriváltakból ez adódik:

Ebből még nagy merészség arra gondolni, hogy sin α = sin β, de ez vezetne arra, hogy a három szög mindegyike 120º.

Az minimális szakaszösszeget a következőképpen számíthatjuk ki. Az ABC háromszögben a szokásos jelölések mellett az I az Izogonális pont, IA szakasz hossza legyen x, az IB szakasz hossza legyen y és az IC szakaszé z, a rajz szerint.

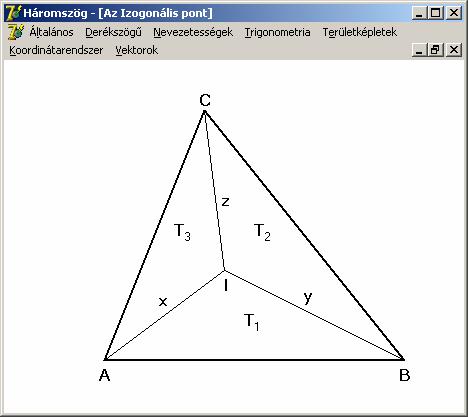
Írjuk fel a három kis háromszög területét:

Ahol

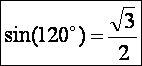
A koszinusz tétel alapján az oldalak négyzete:

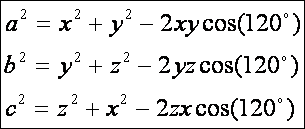
Ahol

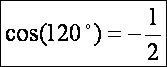
A szögfüggvényértékeket beírva, a következőket kapjuk:

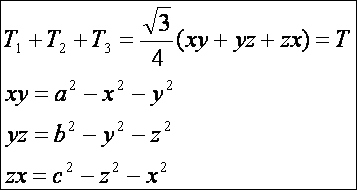
ahol T a háromszög területe. Ezekből x+y+z négyzete előállítható az oldalak és a terület segítségével. Az xy, yz és zx értékeit a T bal oldalába helyettesítve:

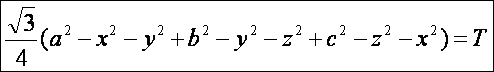
Ebből ezt kapjuk:

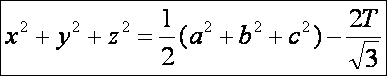
Ezt és a

egyenleteket összeadva x+y+z négyzete adódik.

Azaz az I mértéke (az x, y és z összege):

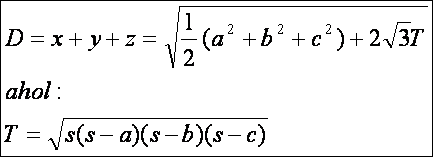
a jól is mert Heron képlet.

Talán egy kicsit több munkával az x, y és z értékeit külön-külön is meghatározhatjuk. A koszinusz tételes egyenletekből kettő így írható fel:

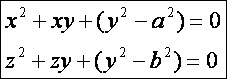
Fogjuk fel ezeket másodfokú egyenleteknek x és z -re nézve. Így a két megoldás:

Tehát:

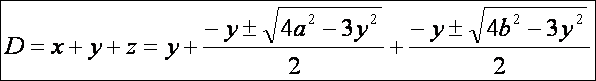
Rendezés és kétszeri négyzetre emelés után újra rendezve ezt kapjuk:

Ebből y -ra a következő adódik (szorzattá alakítások után):

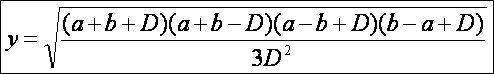
Ez hasonlít egy kicsit a Heron képletre. Hasonlóan:

Ahol tehát

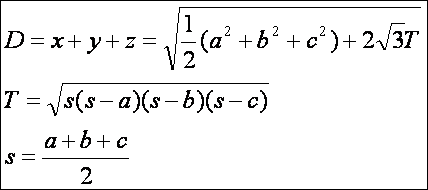
Vagyis a területet a Heron képlettel számolhatjuk, míg s a fél-kerület.

2. Második esetben a háromszög egyik szöge legalább 120º-os. A feladat megoldási pontját a továbbiakban is jelöljük I-vel. Ha ekkor is végrehajtjuk az előző esetben leírt látószög-szerkesztést, de a három körív nem fogja egymást metszeni a háromszög belsejében. Ha a háromszög egyik szöge pont 120º, akkor ebben a csúcsban metszik egymást, vagyis a kerületén. Természetesen ez megegyezik az általunk keresett I-vel, mértéke pedig a háromszög két rövidebb oldalának a hossza. Ha a háromszög egyik szöge nagyobb, mint 120º, akkor is ez a csúcs lesz az I. Bizonyításhoz tekintsük a következő ábrát (a C csúcsnál lévő szöge nagyobb mint 120º):

Az ABC háromszögön kívül vegyük fel az I pontot. Azt kellene belátni, hogy az AC + CB < IA + IB + IC az I helyétől függetlenül. Az AC meghosszabbításának és az IB metszéspontja legyen K. Felírhatók a következők:

AK = AC + CK < IK +I A

CB < CK + KB

Adjuk össze a két egyenlőtlenséget:

AC + CK + CB < IK + IA + CK +KB

CK mindkét oldalon szerepel, ezeket kivonhatjuk, valamint IK + KB = IB. Azaz:

AC + CB < IA + IK + KB = IA + IB

Ha a jobb oldalt IC-vel növeljük, akkor az egyenlőtlenség még élesebb lesz. Azaz:

AC + CB < IA + IB + IC.

A Simson egyenes.

Ha egy háromszög köré írt körének tetszőleges pontjából a háromszög oldalainak egyenesére merőlegeset bocsátunk, akkor a merőlegesek talppontjai egy egyenesre illeszkednek. Ezeket az egyeneseket Simson egyeneseknek nevezzük.

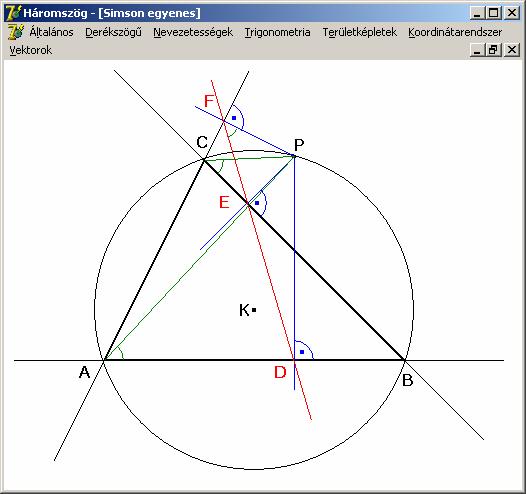
Tekintsük a fentebbi rajzot. Az ABC háromszög K középpontú köré írható körének legyen P egy tetszőleges pontja. Állítsunk P-ből merőlegeseket mindhárom oldal oldal-egyenesére. A merőlegesek (kék színnel rajzolva) az oldalakat rendre D, E és F pontokban metszi. Ezeknek a merőlegeseknek köszönhetően az ADPF és az EPFC négyszögek húrnégyszögek, hiszen szemközti szögeinek összege 180º. A kerületi szögek tétele miatt a húrnégyszög bármely oldala a szemközti csúcsaiból ugyanolyan nagyságú szög alatt látszik. Ezt felhasználva:

Az egyenlőségsor első és utolsó eleme szerint az FE és FD szakaszok egymásra esnek, azaz az F, E és D pontok egy egyenesre esnek, amit a tétel is állít, és ezzel ezt bebizonyítottuk.

Erdős-Mordell tétele.

A háromszög tetszőleges belső pontjának a csúcsoktól mért távolságösszege nem lehet kisebb az oldalaktól mért távolságösszeg kétszeresénél. (A három oldaltól mért távolságösszeg a legnagyobb oldallal szemközti csúcsban a legkisebb.) Egyenlőség csak akkor áll fenn, ha a háromszög szabályos és az adott pont a háromszög középpontja.

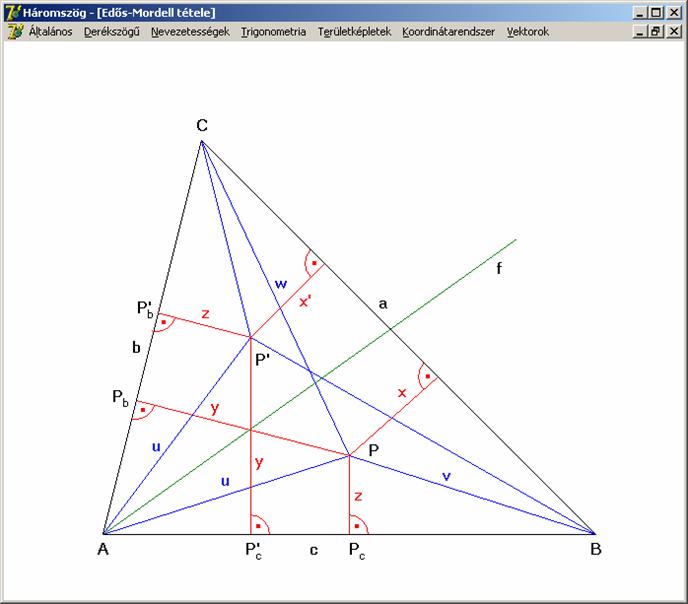
Tekintsük az előző rajzot. Felvettük rajta az ABC háromszög A csúcsánál lévő szög f szögfelezőjét. Erre a szögfelezőre tükröztük a P pontot, így kaptuk a P’-t. A P-nek és a P’-nek az b és c oldalakra eső merőleges vetületei legyenek P_b és P_c, illetve P’_b és P’_c. A tükrözés miatt AP = AP’ = u. A szögfelezőre való tükrözés miatt a PAP_c és P’AP’_b szögek, valamint a P’_cP’A és APP_b szögek egyenlők, így az érintett derékszögű háromszögek egybevágók, amiből: P’P’_c = PP_b = y és PP_c = P’P’_b = z adódik. A bizonyításhoz használjuk fel a négyszögek következő területképletét, illetve a belőle adódó egyenlőtlenséget:

Ahol e és f a négyszög átlói és ε pedig a két átló által bezárt szög. Alkalmazzuk ezt az egyenlőtlenséget az ABP’C négyszögre:

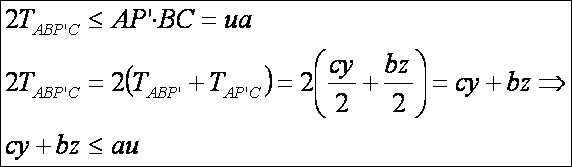
Hasonlóan a további szakaszokra:

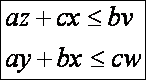
Mindebből az adódik, hogy:

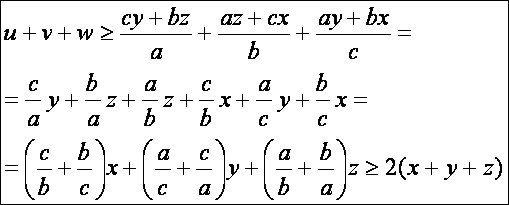
Ez utóbbi átalakítás pedig azért érvényes, mert egy nem nulla számnak és a reciprokának összege mindig nagyobb vagy egyenlő, mint kettő. Egyenlő csak akkor lehet, ha a szám 1-el egyenlő. Ebből viszont az adódik, hogy a = b = c, azaz a háromszög szabályos.

A Morley háromszög.

Ha egy háromszögben megrajzoljuk a szögeinek harmadoló egyeneseit, akkor azoknak a harmadoló-egyeneseknek a metszéspontjai, amelyek egy-egy oldalhoz közelebb haladnak, minden háromszögben egy szabályos háromszögnek a csúcsai.

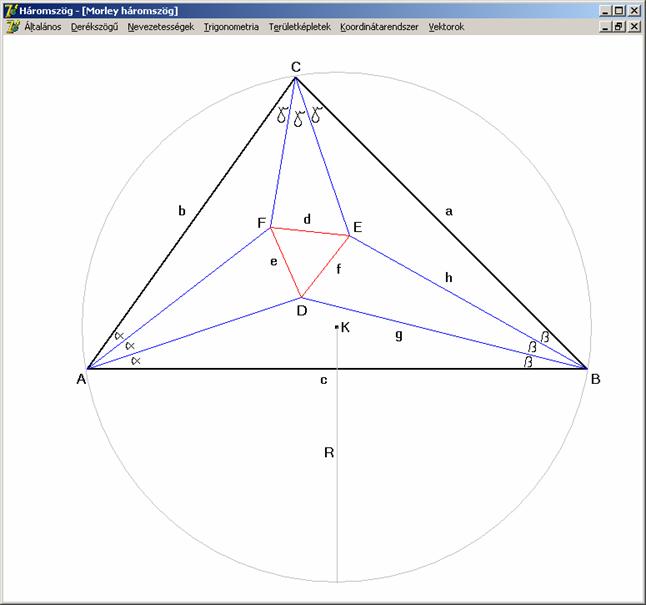
A bizonyításhoz használjuk az előző rajzot és annak jelöléseit.

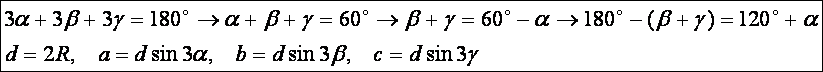
Írjunk fel egy szinusz tételt a BEC háromszögre és alkalmazzuk a szögek közötti összefüggéseket és helyettesítsük be a-nak a fenti kifejezését:

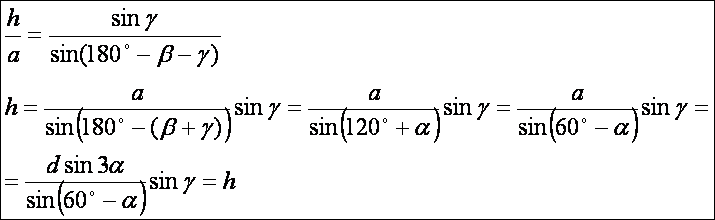
Számoljuk ki, majd célszerűen alakítsuk át a háromszoros szögek szinuszára érvényes képletet:

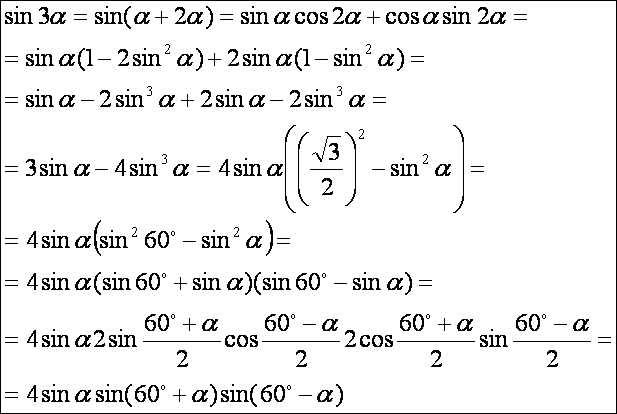
Helyettesítsük be ezt a h képletébe:

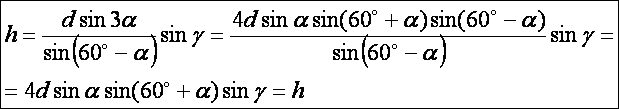
Hasonlóan kaphatjuk g-t:

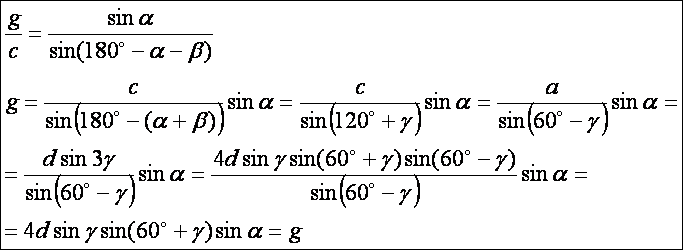
Írjunk fel a BDE háromszögre koszinusz tételt:

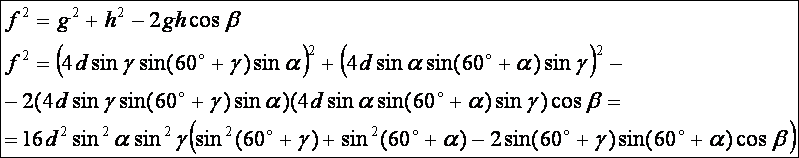
A képlet harmadik tényezőjének zárójeles része – amely maga egy koszinusz tétel a több tagot tartalmazó oldalához hasonlít – a béta szög szinuszának a négyzete. Van ugyanis olyan x, y és z oldalú háromszög, amelynek a köré írható köre egységnyi átmérőjű, és amelyet ezen a rajzon láthatunk:

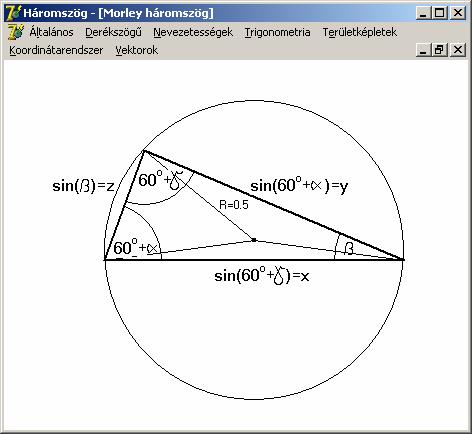
Szögei nyilván:

Oldalai és a koszinusz tétel:

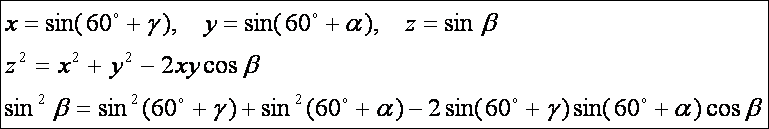
Ezt visszahelyettesítve a BDE háromszög koszinusz tételébe:

Mivel a levezetésben nem használtuk ki, hogy az a oldalhoz kapcsolódó szögharmadolókat használtuk fel, így a DEF háromszög minden oldalára ugyanez adódik, azaz ez a háromszög szabályos:

Malfatti feladata.

Szerkesszünk egy háromszögbe három egymást és a háromszög két-két oldalát érintő kört.

A Matematika Lexikon alapján a feladat megoldása: a háromszög fél-kerületét egységnek véve szerkesszünk olyan szögeket, amelyek szinuszának négyzete a háromszög oldalaival egyenlő. Majd megszerkesztjük a 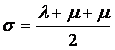szög segítségével a szögeket. Végül megrajzoljuk a szögek szinuszának négyzetét. Ez utóbbi három szakasz lesz a háromszög csúcsaiból a Malfatti-féle körökhöz húzott szakaszok a háromszög oldalain. A megoldás indoklásához tekintsük a következő rajzot:

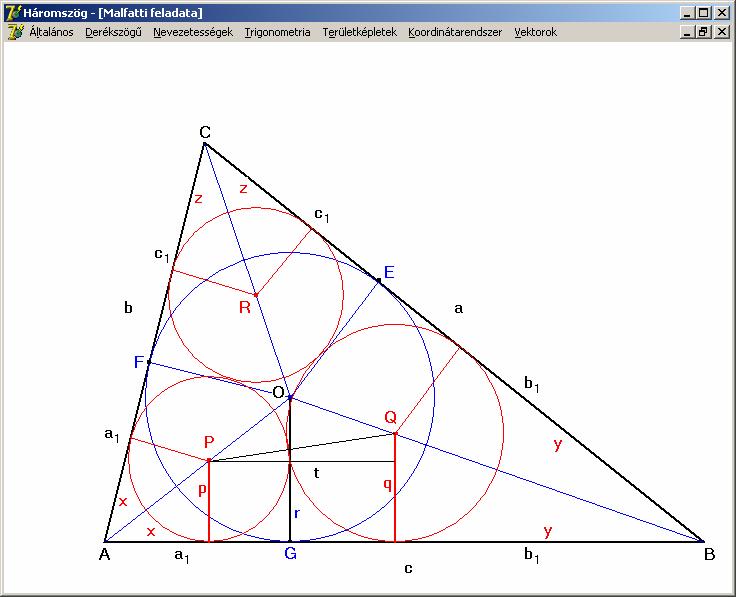
A kék színnel rajzolt kör az ABC háromszögbe beírt kör, melynek r a sugara és O a középpontja. Ez a kör az oldalakat az E, F és G pontokban érinti. Az érintő szakaszok hossza: AG = AF = a₁ = s - a, BG = BE = b₁ = s - b és CE = CF = c₁ = s – c. A piros színnel rajzolt körök a feladat megoldását jelentő Malfatti-féle körök. Ezek érintő szakaszai x, y és z. Mivel a P és O pont is az A csúcsnál lévő szög szögfelezőjén van, így p/r = x/a₁. Hasonlóan a B csúcsnál lévő szög szögfelezőjén a Q és O pontok vannak rajta ezért: q/r = y/b₁. A PQ = p + q szakasz egy olyan derékszögű háromszög átfogója, melynek az egyik befogója a t-vel jelölt szakasz. A másik befogója q – p. Írjunk fel erre a háromszögre Pitagorasz tételt és t-be helyettesítsük be a p-t és q-t az előbbi aránypárból kifejezve (használjuk továbbá a Heron képletet – s(s - a)(s - b)(s - c) = sa₁b₁c₁ – , ahol s a fél-kerület):

Ezek alapján a háromszög AB oldala:

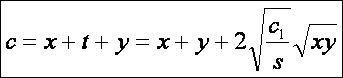
Ugyanígy kapható a másik két oldalra:

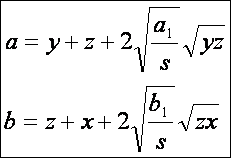
Most tekintsük a fél-kerületet egységnek:

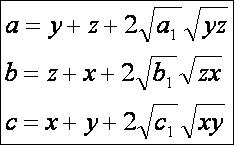
Tekintsük az a, b, c, x, y és z (egynél kisebb) értékeket a hegyesszögek szinuszainak négyzeteként, azaz:

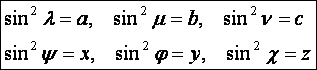
Továbbá, mivel a + a₁ = s = 1, b + b₁ = s = 1 és c + c₁ = s = 1, így a trigonometrikus Pitagorasz-tételt is felhasználva:

Az utóbbiakat felhasználva a fenti egyenletrendszer ilyen alakú lesz:

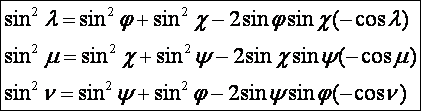
Ha az első egyenletet tekintjük, akkor az nem más, mint a sin λ oldalra felírt koszinusz tétel a sin φ, sin χ oldalú háromszögben, ahol λ = φ + χ a háromszög külső szöge. Ez utóbbinak megfelelő összefüggés a további két egyenletből is kiolvasható, azaz összegezve:

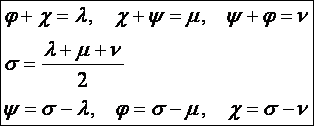
Ezzel a fentebb leírt szerkesztési eljárást megindokoltuk.

Következő lap: http://gorbem.hu/MT/Haromszog6.htm