Differenciálgeometria (6)
Görbesereg, burkoló, diszkrimináns görbe
Egy vagy több paramétertől függő görbék halmazát görbeseregnek nevezzük. Görbesereget
kapunk például, ha egy tetszőleges görbét egy ka
vektorral eltolunk, ahol a
egy konstans vektor, a k pedig egy tetszőleges valós
paraméter (akár végtelen sok értékkel). Görbesereg például azon kétegységnyi
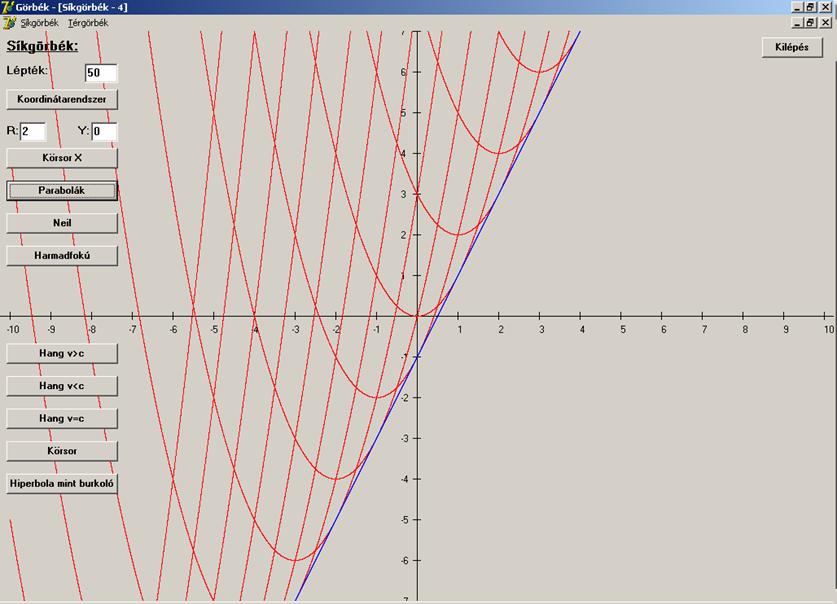
sugarú körök halmaza, melyeknek a középpontjai az x tengelyen vannak. Görbesereg az összes olyan parabola, mely az y = x2 eltolásából
keletkezik úgy, hogy azok érintik az y =
2x-1 egyenest. De görbesereg például egy henger összes csavarvonala. Ez
utóbbi térbeli, kétparaméteres görbesereget alkot. Az említett két síkbeli
görbesereg rajzban:
![]()
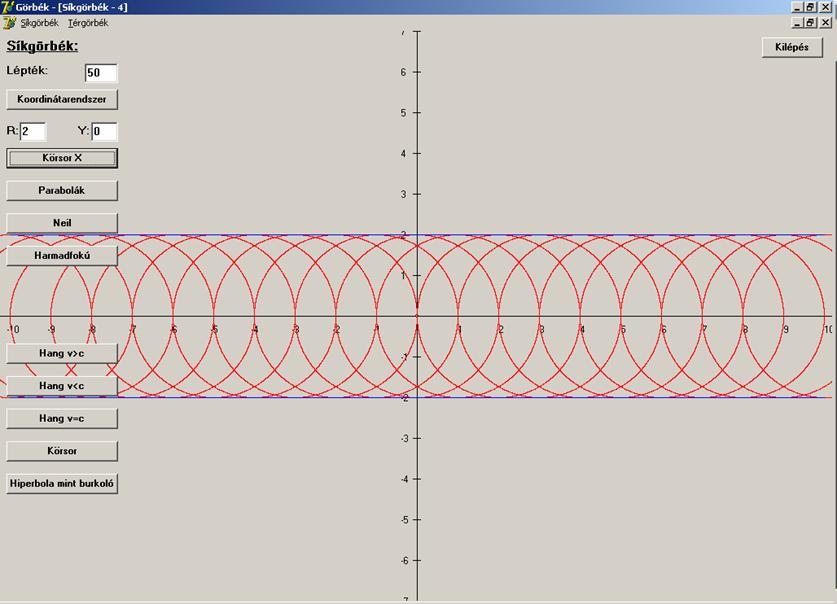
![]()
Egy síkbeli görbesereg burkolójának nevezünk egy olyan görbét, amelynek
-
a sereg minden görbéjével egyetlen közös pontja van,
-
a közös pontokban a burkoló érinti a sereggörbét.
A továbbiakban csak síkbeli görbeseregekkel
foglalkozunk. Legyen adva egy görbesereg a következő implicit formában: F(x, y, c) = 0 (ahol F kétszer deriválható függvénye a változóinak). Ahhoz, hogy egy x = x(c), y = y(c) görbe burkolója
legyen az F(x, y, c) = 0
görbeseregnek szükséges, hogy:
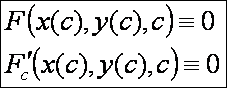
teljesüljön.
A fenti két síkbeli példában a görbesereg burkolói:
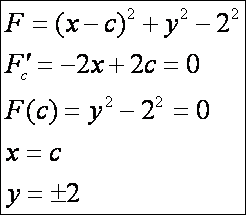
A
parabolák esetén:
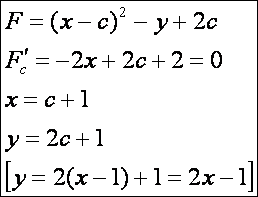
A
fenti szükséges feltétel még nem elégséges ahhoz, hogy az x = x(c), y = y(c) burkoló legyen. A
szükséges feltételeket teljesítő görbét diszkrimináns görbének nevezzük.
Lássunk példát olyan görbeseregre, hogy a feltételeket teljesítő görbe nem
burkoló.
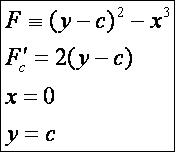
Ennek
a görbeseregnek az x = 0, y = c
egyenesen csúcspontjai vannak (Neil-féle parabolák),
azaz az x = 0 egyenes egy
diszkrimináns görbe (kék színnel jelölve):
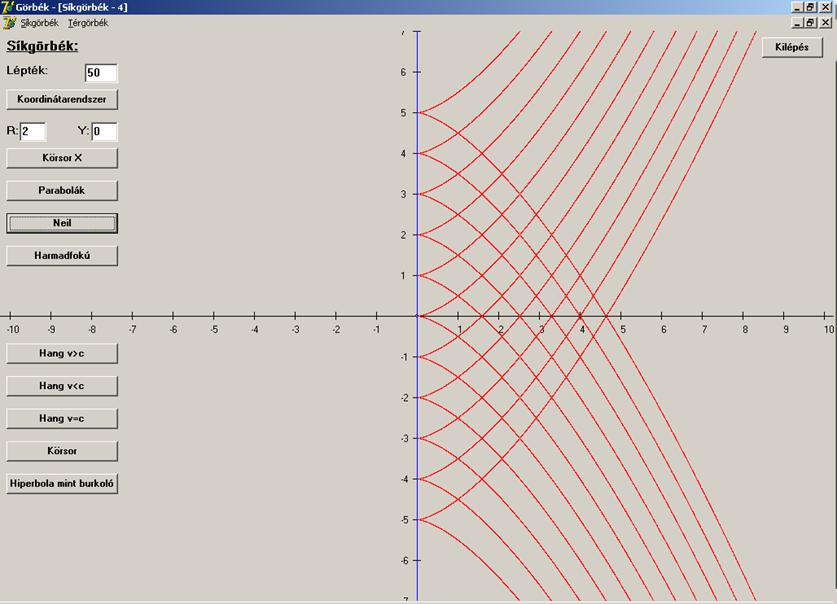
Tehát
az egyenesnek valóban egy közös pontja van a görbesereg elemeivel, de a
csúcspontok miatt nem érinti azokat, ezért nem burkoló. Ha egy
diszkrimináns-görbére még a következők is teljesülnek (elegendő feltétel),
akkor biztosan burkoló lesz:
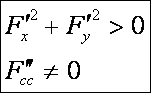
Most nézzünk egy olyan példát, amely arra mutat rá,
hogy az elegendő feltétel nem szükséges. Tekintsük a következő görbesereget és
burkolóját:
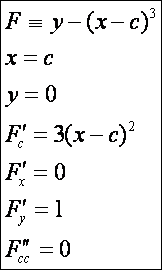
Ebben
a példában az y = x3
harmadfokú parabolákból álló görbeseregről van szó. Ennek az x tengely a burkolója (kékkel jelölve, mely
érint és egy közös pont van, habár metszi is a
görbéket), holott a második derivált minden c-ben eltűnik, azaz az elégséges feltétel második része nem
teljesül.
Mivel többek között fizikatanár is vagyok, talán érthető
a következő példa: mozogjon egy hangforrás egyenes vonalú egyenletes mozgással
egy olyan közegben, melyben a hangnak a terjedési sebessége c = Mach. A
jelenség térbeli, de most csak síkban ábrázolnám (a valóság a rajzok x tengely körüli megforgatásával állítható
elő). Ha a hangforrás v sebessége a hang terjedési sebességénél nagyobb, azaz a hangforrás
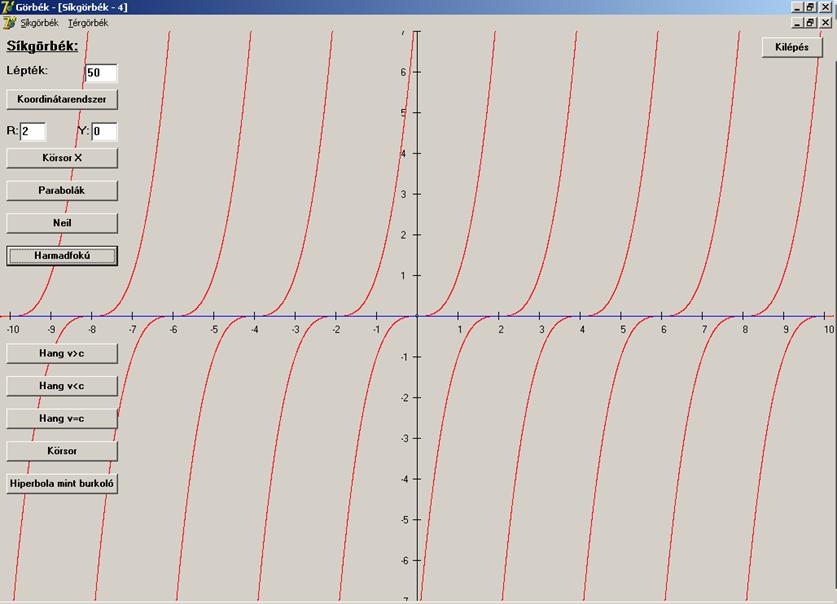
elhagyja saját hangját (legyen például a
kétszerese), akkor egy hangkúp keletkezik.
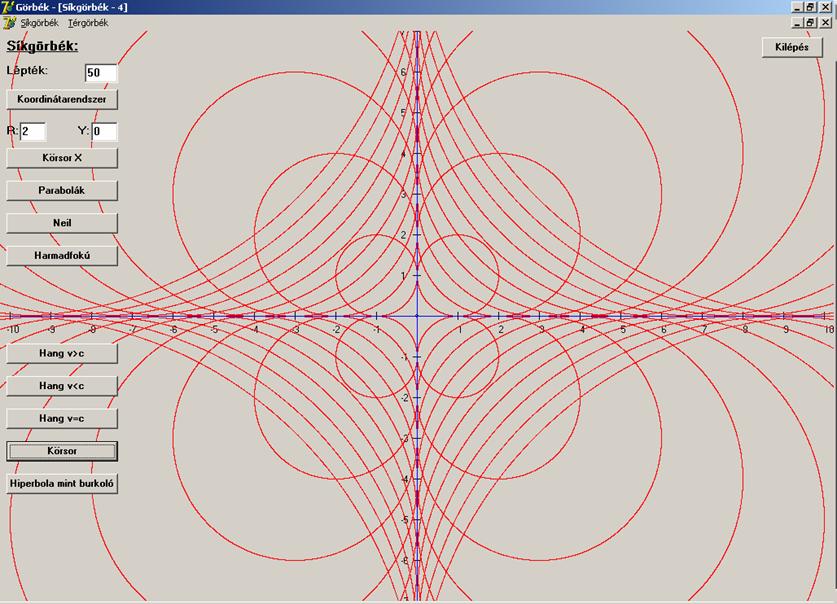
A jelenség síkbeli megfelelője esetén egy körsereget kapunk, melynek burkolója
két félegyenes (térbeli megfelelője a hangkúp, mely a saját felületére
merőleges irányban halad, vagy növekszik Mach
sebességgel):
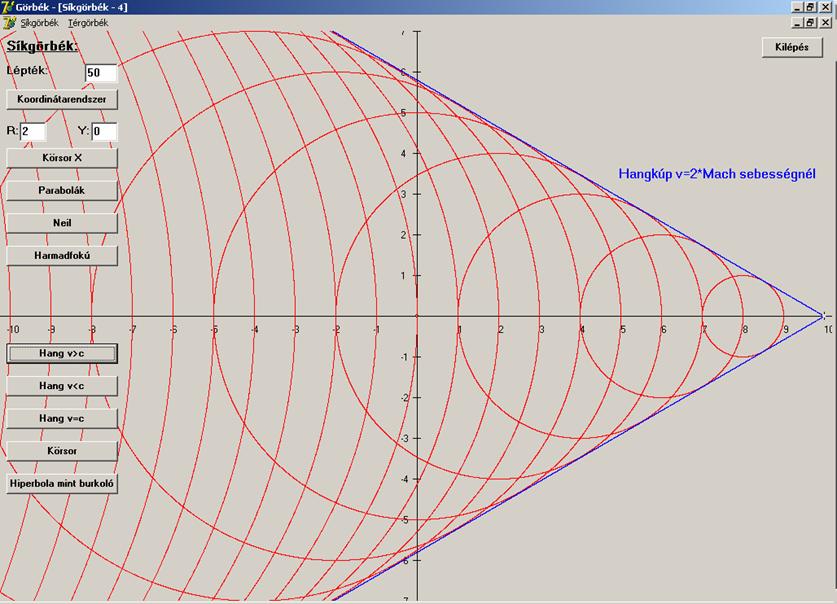
Ha
a hangforrás sebessége kisebb, mint a Mach, akkor is
kapunk a síkbeli leképezéskor körsereget, csak ekkor burkolója nem létezik.
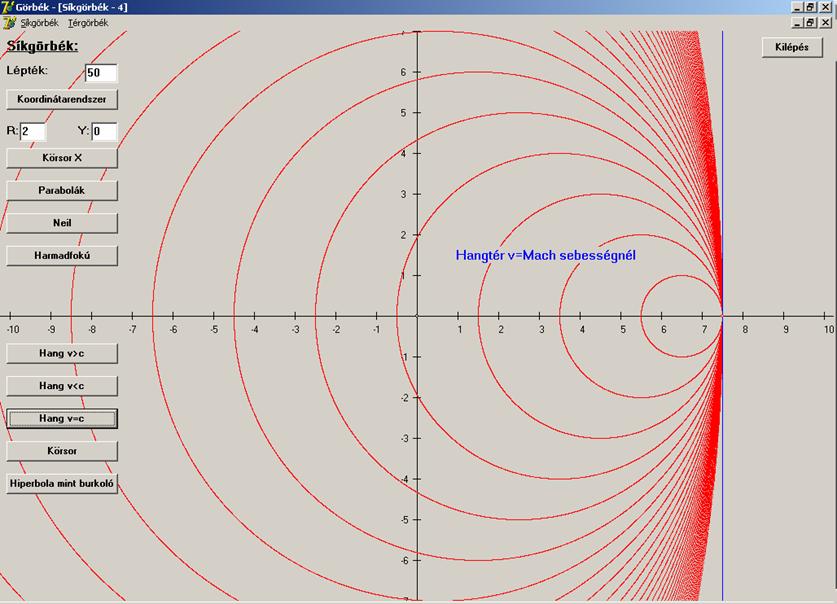
Ilyenkor a hangtér így néz ki (síkban):
Ha
a hangforrás a térben pontosan a Mach sebességgel
akar menni (fizikailag ez eléggé nehézkes), akkor hangkúp helyett egy hangsík
keletkezik, ahogy az alábbi rajzon látható. Ez a hangsík Mach
sebességgel halad a hangforrással egyező irányban, vele együtt.
Az
első és a harmadik esetben fellép az úgynevezett hangrobbanás. Látható, hogy a
második esetben a tér minden pontjára a hanghullámok időben elosztva érkeznek
meg, itt legfeljebb a Doppler-jelenség figyelhető meg (ez a frekvencia
eltolódás: közeledő hangforrásnál a magasabb, távolodónál mélyebb hangok felé).
Nem így például az első esetben. Ekkor a hangkúp előtt még nem hallunk semmit,
viszont amikor megérkezik a hang, akkor egy adott pontban sok, egymástól
különböző pontból induló hanghullám éri el a megfigyelőt, és ezeknek
a hanghullámoknak az ereje összeadódik, vagyis erős hanghatást, hangrobbanást
hallunk. Ez a hanghatás károsíthatja az élőlényeket, és épített környezetünket.
Szuperszonikus, azaz Mach feletti repülésnél is megfigyelhető
hangrobbanás. Ilyen volt például a francia Concorde
gép, amiknek a Mach feletti repülését csak az Atlanti
óceán felett engedélyezték. A legintenzívebb hatások a v = Mach sebességnél tapasztalhatók.
Kezdetben a repülők ezt csak nehezen tudták átlépni, sőt károsodtak is, esetleg
lezuhantak, mert nem bírta szerkezetük a nagy terhelést. Hogy minél kisebb
ideig haladjanak a repülőgépek a Mach közelében, ma
is legtöbbször süllyedésben (a gravitációs erőt is felhasználva) lépik át ezt a
határt.
Ábrázoljuk a következő görbesereget és határozzuk meg
a görbesereg burkolóját:

A
görbesereg tehát két körsor (az egyik körsor köreinek középpontja az y = x, a másiknak az y = -x
egyenesen vannak), burkolói pedig a koordinátatengelyek:
Határozzuk meg annak a görbeseregnek a burkolóját,
amelynek elemei ugyanakkora, T területű háromszöget zárnak be a koordinátatengelyekkel.
Legyen az egyenesek egyenlete tengelymetszetes:
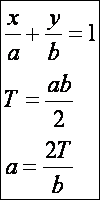
Válasszuk
az b -t a
görbesereg paraméterének (T = állandó).
A görbesereg egyenlete:
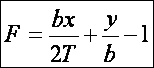
Megmutatjuk,
hogy ennek a görbeseregnek a burkolója az xy = T/2 hiperbola. Legyen a hiperbola paramétere is b:
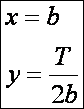
Ezeket
a görbesereg egyenletébe és annak deriváltjába helyettesítve b -t
meghatározhatjuk:
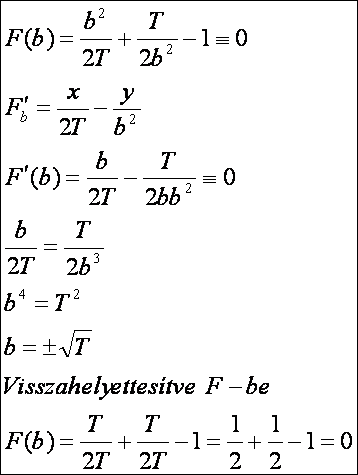
Ez
utóbbi pedig azt bizonyítja, hogy a megadott hiperbola valóban burkoló. Mivel a
T csak pozitív lehet de a és b negatív is, a burkoló másik
függvénye: xy = -T/2. Lássuk mindezt ábrázolva:

Ebben a példában az Ax + By + C = 0 egyenes seregnek az x2 + y2 = R2
kör a burkolója. Határozzuk meg, milyen feltételeknek kell eleget tenni az A, B és C együtthatóknak.
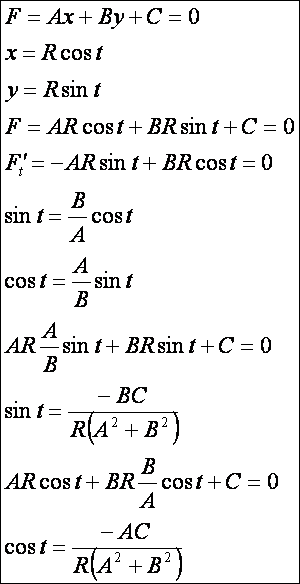
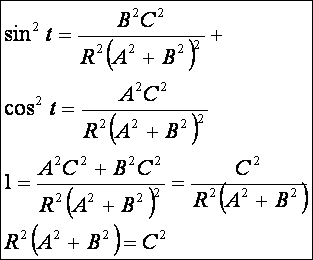
Evolúta
Legyen az ![]() síkgörbe olyan, hogy
görbületének differenciálhányadosa sehol sem tűnik el. Ekkor az
síkgörbe olyan, hogy
görbületének differenciálhányadosa sehol sem tűnik el. Ekkor az
![]() evolútáján értjük görbületi
középpontjainak a mértani helyét. Ha az evolútát
evolútáján értjük görbületi
középpontjainak a mértani helyét. Ha az evolútát ![]() jelöli, akkor
egyenlete:
jelöli, akkor
egyenlete:
![]()
Általában
az s nem ívhossza az
![]() evolútának.
evolútának.
Ha a görbét paraméteres egyenletrendszerrel (x = f1(t),
y = f2(t)) adjuk meg, akkor az evolúta
egyenlete:
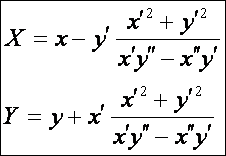
Írjuk fel és rajzoljuk is meg néhány görbe evolútáját. Első görbénk legyen az ellipszis:
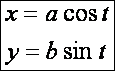
Az
evolútája:

Mindez
rajzban:
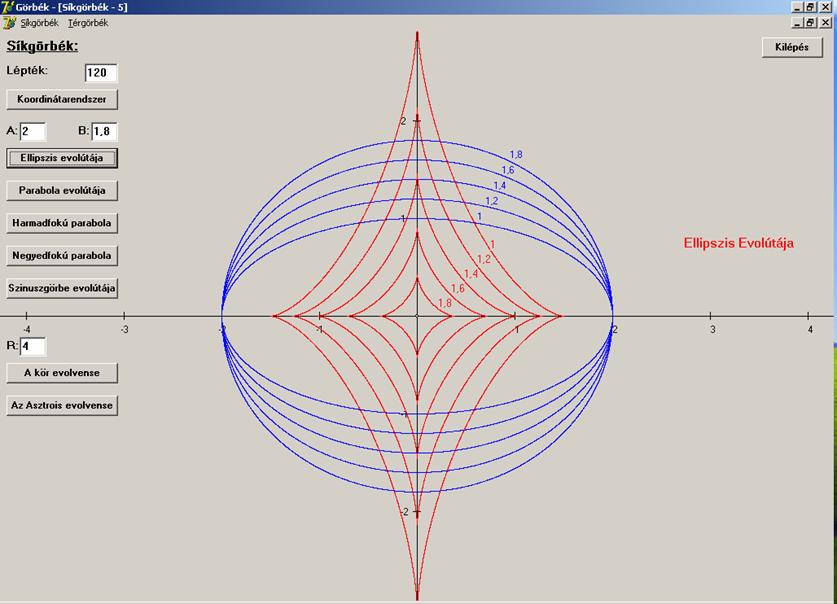
A
rajzon öt ellipszis és az evolútája látható. Az
ellipszis nagytengelye állandó (a = 2),
a kistengelyt 1 -ről
1,8 -ra növeltük. A könnyebb azonosítás végett az egymáshoz
tartozó görbéket ugyanazzal a számmal jelöltük. Az ellipszis evolútája egy négy csúcspontú görbe. A csúcspontok ott
jönnek létre, ahol az ellipszis görbületének szélső értéke van. Éppen ezeket a pontokat vettük ki a vizsgálatainkból, amikor azt
feltételeztük, hogy a görbület első deriváltja sehol sem tűnik el. Minél
kevésbé különbözik a kis- és nagytengely, az evolúta
területe annál kisebb lesz. Ha az ellipszis egyenletében a = b -t választunk, akkor kört kapunk. Az
egyenletekből látható, hogy ekkor az evolúta a kör
középpontjává zsugorodik.
Második legyen a parabola:
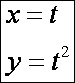
Az
evolútája:
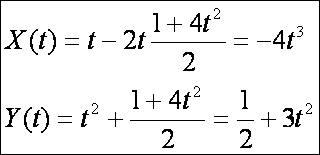
Megrajzolva:
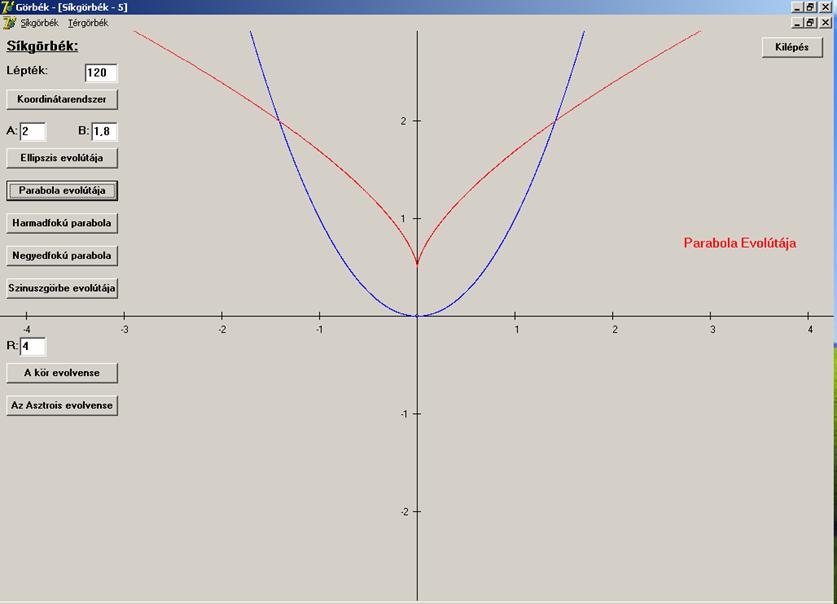
Itt
is látható, hogy a csúcspont a parabola legkisebb görbületéhez tartozik.
Most vizsgáljuk meg a harmadfokú parabolát:
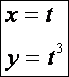
Evolútája:

Rajzban:
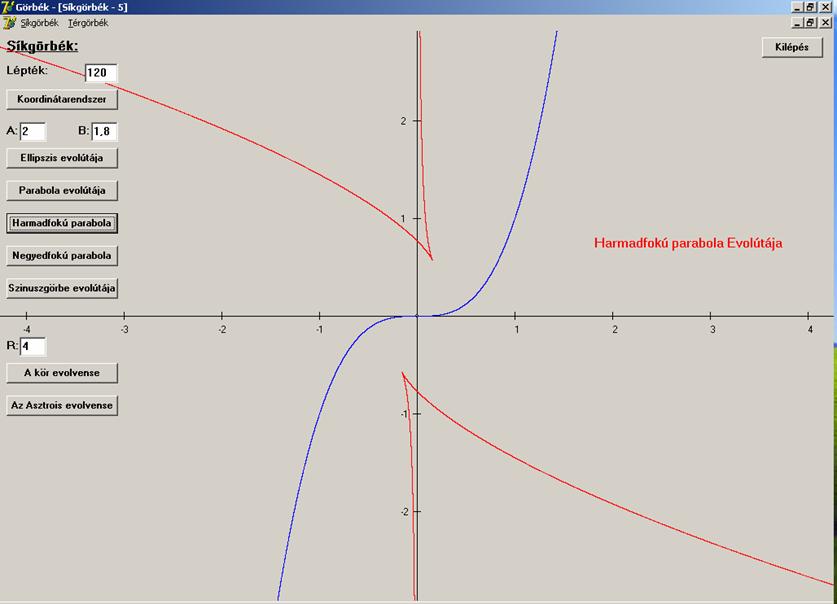
Ennek
az evolútának is van két csúcspontja.
Nézzük meg a negyedfokú parabolát is:
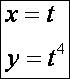
Az
evolútája:
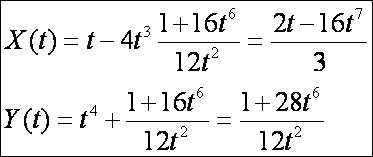
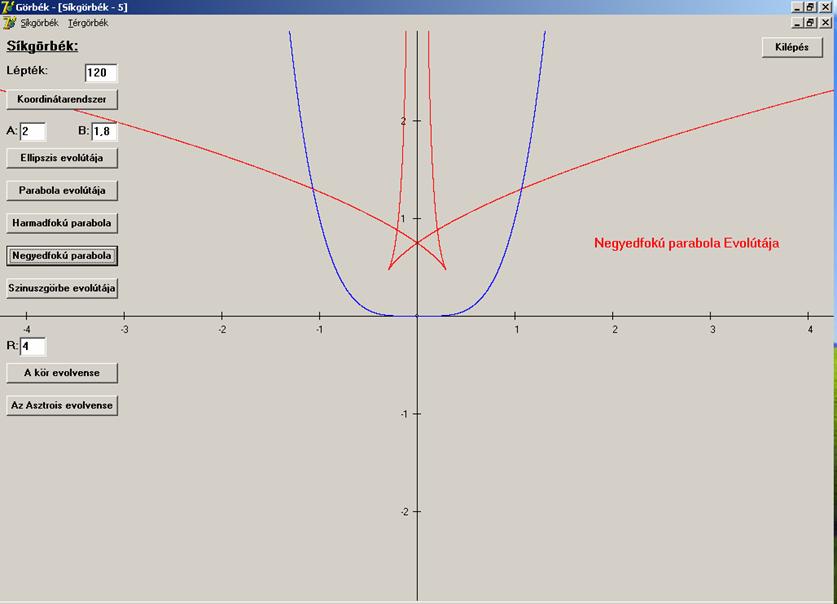
Rajzban:
Semmi
különös, ennek az evolútának is van két csúcspontja.
Végül lássuk a szinuszgörbét:
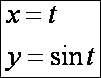
Ennek
evolútája:
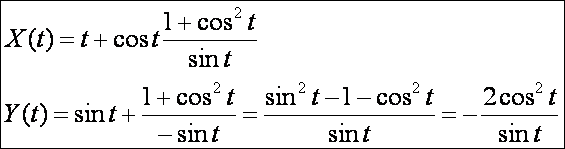
Megrajzolva:
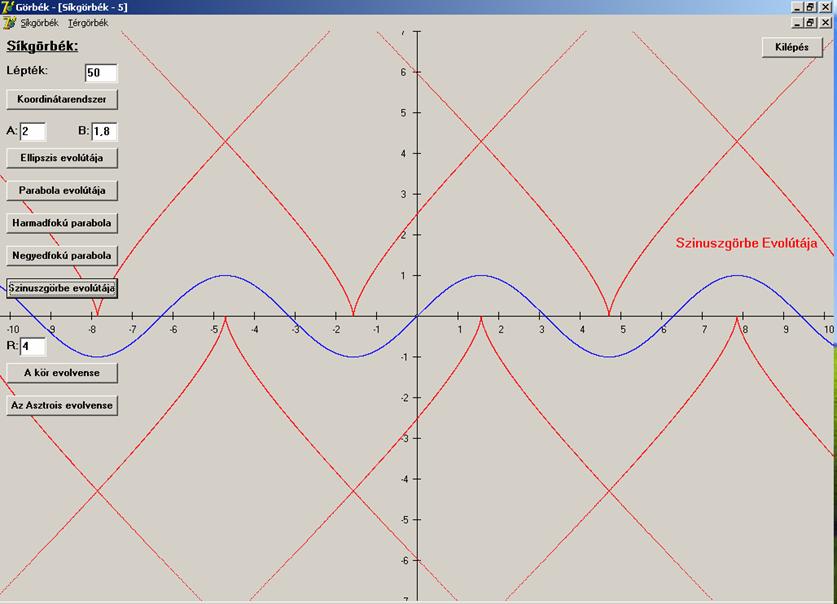
A
csúcspontmentességet itt sem úsztuk meg. A szinuszgörbe minden szélsőérték
helyéhez tartozó pontban az evolútájának csúcspontja
van.
Evolvens
Legyen az ![]() síkgörbe olyan, hogy
görbületének differenciálhányadosa sehol sem tűnik el. Ekkor az
síkgörbe olyan, hogy
görbületének differenciálhányadosa sehol sem tűnik el. Ekkor az
![]() evolvensén a görbe érintőit
végig merőlegesen metsző vonalakat értünk. Tehát nem egy görbéről, hanem egy
görbeseregről van szó. Ezeket a vonalakat szokták a
görbe ortogonális (azaz merőleges) trajektóriáinak is
nevezni. Ha a görbe evolvenseit
evolvensén a görbe érintőit
végig merőlegesen metsző vonalakat értünk. Tehát nem egy görbéről, hanem egy
görbeseregről van szó. Ezeket a vonalakat szokták a
görbe ortogonális (azaz merőleges) trajektóriáinak is
nevezni. Ha a görbe evolvenseit ![]() jelöli, akkor
egyenlete:
jelöli, akkor
egyenlete:
![]()
![]() képletében
s>s0, ahol s0 a seregparaméter. Ennek a
képletnek a helyességét deriválással könnyű belátni, hiszen:
képletében
s>s0, ahol s0 a seregparaméter. Ennek a
képletnek a helyességét deriválással könnyű belátni, hiszen:
![]()
Látható,
hogy a ![]() érintője főnormális irányú, azaz merőleges a görbe érintőjére. Az evolvens egyszerű szerkesztési módja a következő: ha
görbére az s0 ponttól
kiindulva egy fonalat görbítünk, majd ezt egy s pontban rögzítjük. Ha utána a fonalat kifeszítve az s0-tól kezdve lefejtjük,
akkor az s0 -ból induló pont egy eveolvenst
ír le. Ebben az s0
pontban az evolvensnek csúcspontja van (nem mehet át
a görbén).
érintője főnormális irányú, azaz merőleges a görbe érintőjére. Az evolvens egyszerű szerkesztési módja a következő: ha
görbére az s0 ponttól
kiindulva egy fonalat görbítünk, majd ezt egy s pontban rögzítjük. Ha utána a fonalat kifeszítve az s0-tól kezdve lefejtjük,
akkor az s0 -ból induló pont egy eveolvenst
ír le. Ebben az s0
pontban az evolvensnek csúcspontja van (nem mehet át
a görbén).
Az evolvens és az evolúta egyfajta duálisai egymásnak. Ugyanis az ![]() görbe bármely
görbe bármely ![]() evolvensének
az evolútája az
evolvensének
az evolútája az ![]() . Megfordítva:
. Megfordítva: ![]() görbe
görbe ![]() evolútájának
egyik evolvense az
evolútájának
egyik evolvense az ![]() . Továbbá az is igaz, hogy az evolúta
s1 és s2 paraméterű pontjai közé
eső ívének a hossza az eredeti görbe s1
és s2 paraméterű
pontjaiban vett görbületi sugarainak különbségével egyenlő. Jelölje
. Továbbá az is igaz, hogy az evolúta
s1 és s2 paraméterű pontjai közé
eső ívének a hossza az eredeti görbe s1
és s2 paraméterű
pontjaiban vett görbületi sugarainak különbségével egyenlő. Jelölje
![]() az
az ![]() evolúta
ívhosszát. Ekkor:
evolúta
ívhosszát. Ekkor:
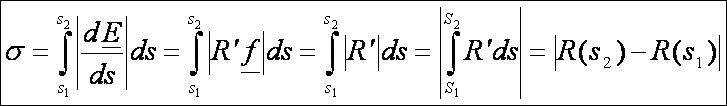
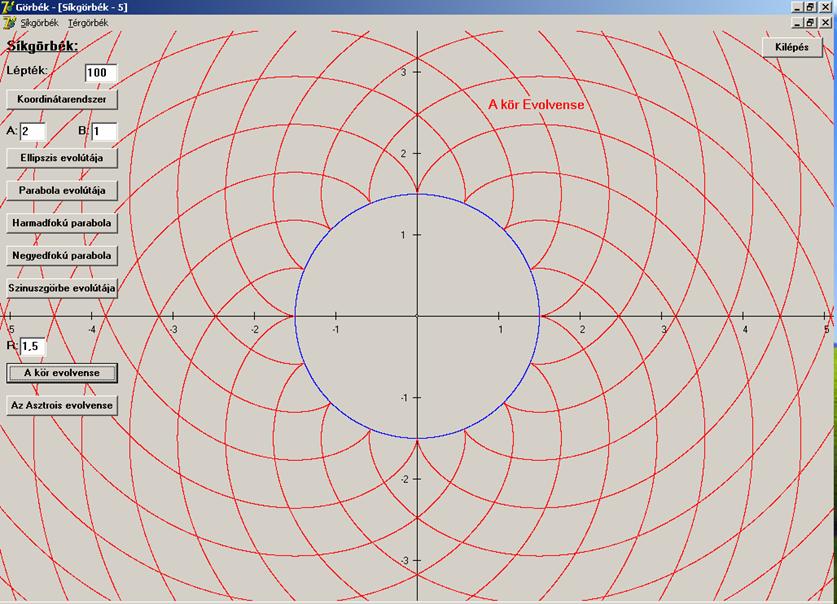
Írjuk fel és rajzoljuk is meg néhány görbe evolvensét. Kezdjük a körrel.
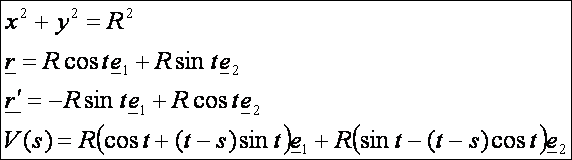
Mindez
rajzban:
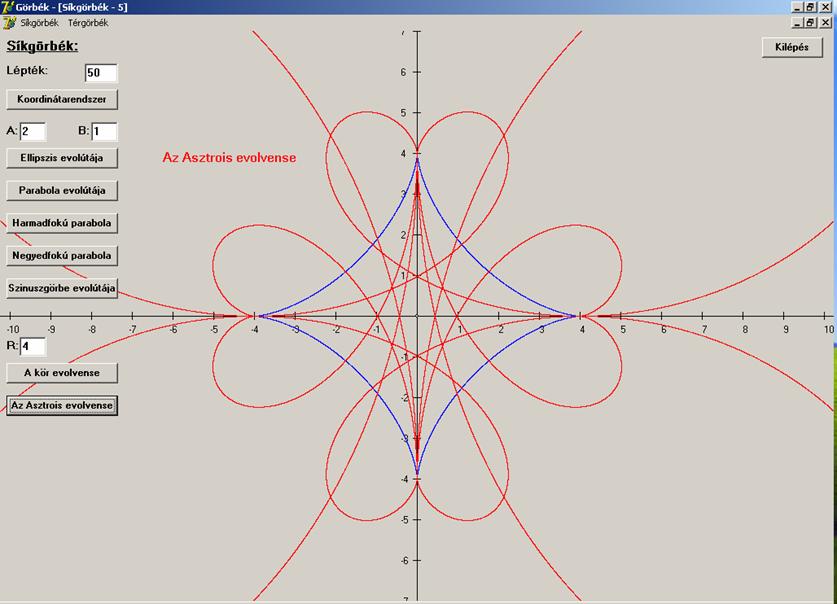
Az Astrois és evolvense:
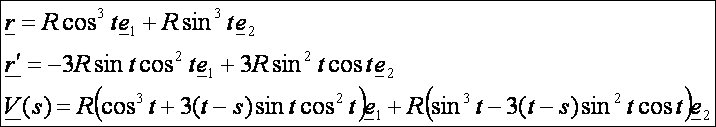
Mindez
rajzban:
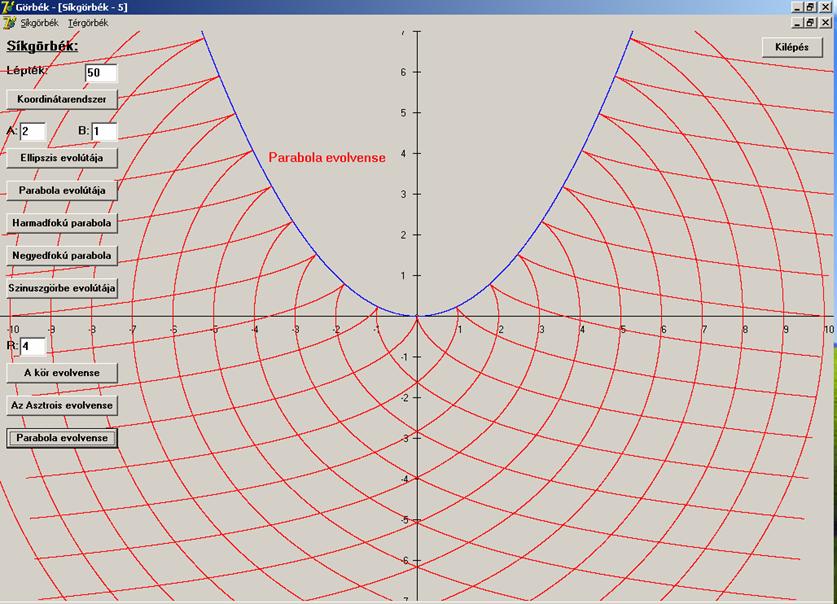
A parabola evolvense:

Rajzban
pedig:
A
fentiek igazolására először számítsuk ki a parabola ívhosszát:

A
határozatlan integrált helyettesesítéssel határozzuk meg:

Hajtsuk
végre ezt a helyettesítést:
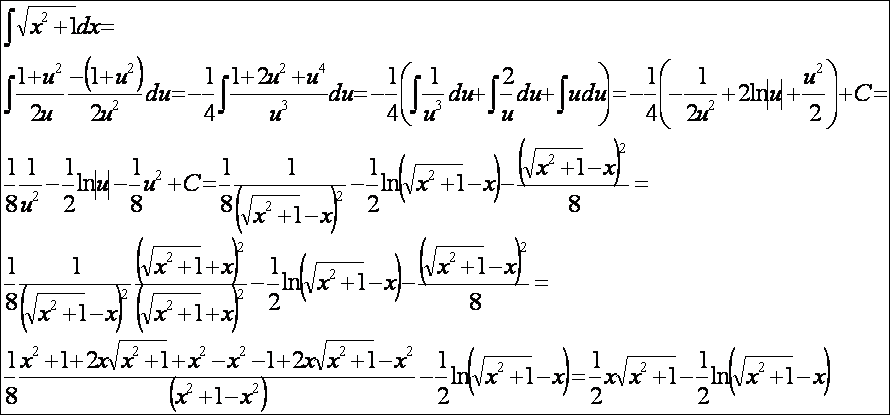
Ezek
alapján az ívhossz:
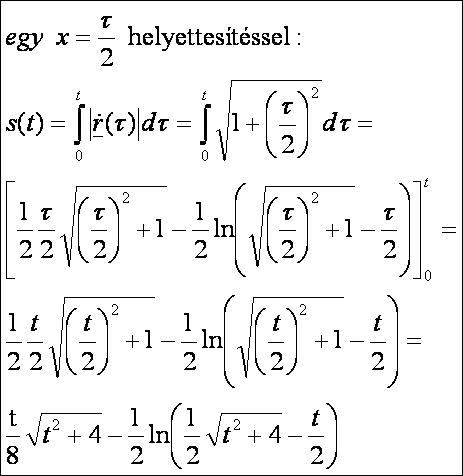
Következő
lap: http://gorbem.hu/MT/DiffGeom7.htm