Differenciálgeometria (4)

Kísérő háromél (triéder)

Vizsgálataink során mindig az egyszerűségre törekszünk. Ezért vezettük be az ívhossz-paramétert is. Ilyen paraméterezés mellett az r’(s) érintővektor egységnyi hosszúságú, melyet t(s) -sel jelölünk. A továbbiakban is ezen az úton haladunk. Tekintsük a következőket:

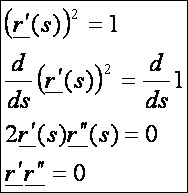
Mindebből az adódik, hogy a második derivált merőleges az első deriváltra, vagy nullvektor. Ha ez nem nullvektor, akkor a második derivált irányába mutató egységvektort főnormálisnak nevezzük és f(s) -el jelöljük, azaz:

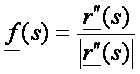
Így a görbe pontjaihoz már két, egymásra merőleges egységvektort rendeltünk (ahol lehetett). Ez a kettő a síkgörbék esetén már alkalmas lokális koordinátarendszernek. De térgörbék esetén még egy egységvektorra van szükség. Ez a vektor lesz a b(s) binormális (merőleges az érintővektorra és a főnormálisra), melyet a t(s) és f(s) vektorok vektoriális szorzataként kapjuk, ezért szintén egységvektor:

E három vektor között természetesen a következők összefüggések is érvényesek:

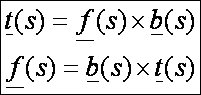
Azaz, az így értelmezett t, f és b vektorok ortonormál jobbrendszert alkotnak, melyet a görbe kísérő triéderének nevezzük. A kísérő triéder egyeneseit a következő egyenletekkel adhatjuk meg:

Az érintő egyenese:

vagy

vagy koordinátákkal:

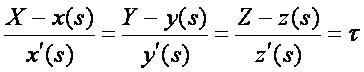
A főnormális egyenese:

vagy

A binormális egyenese:

vagy

Legyen a P₀ a görbe egy olyan pontja melyben az érintő-vektor deriváltja nem tűnik el. Tekintsünk a görbén további három olyan nem kollineáris pontot (P₁, P₂ és P₃), amelyek mindegyike a P₀ -hoz tart. Ezek a pontok minden helyzetükben egy síkot határoznak meg. Ezeknek a síkoknak a sorozata egy olyan síkhoz konvergál, melyet a P₀ -beli érintővektor és főnormális feszít fel, és amely csak a görbétől és P₀ ponttól függ. Ezt a határsíkot a görbe P₀ -beli simuló síkjának nevezzük. A kísérő triéder tehát egy lokális, derékszögű koordinátarendszer, amely három egymásra merőleges síkot határoz meg a következőképpen:

a t és az f a simulósíkot,

az f és a b a normálsíkot,

a b és a t a rektifikáló síkot.

A síkok egyenletei:

Simulósík:

vagy koordinátákkal:

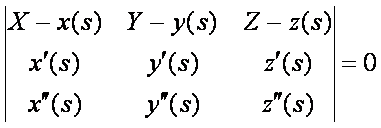
Normálsík:

Rektifikáló sík:

A simulósík és rektifikáló sík egyenletében a vektorok vegyes szorzata szerepel, azaz: abc = (a x b)c. A fenti képletekben az X, Y és Z az l egyenes illetve az L sík általános koordinátái. Az egyenesek és síkok képleteiben konkrét feladat esetén az s alatt mindig egy rögzített s₀ paramétert kell érteni. Az egyenesekre és síkokra vonatkozó egyenletek általános paraméterek esetén ugyanilyen formában érvényesek.

Görbület

A kör esetén, annak az R sugarát, görbületi sugárnak is szokták nevezni. Minél kisebb a kör sugara, annál jobban görbül, minél nagyobb, annál kevésbé. A görbe görbülete azt fejezi ki, hogy mennyire tér el a görbe az egyenestől. Kör esetén a G görbület a sugár reciproka. Hasonlók igazak általános görbe esetén is. Az érintő egységvektor változási sebességének nagysága (szögsebessége) a görbe görbülete, ami egyúttal a görbületi sugár reciproka:

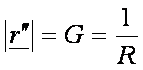
A főnormálissal:

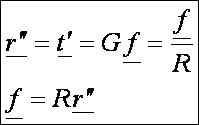
Nyilvánvaló, hogy az egyenes görbülete nulla, így görbületi sugara nem létezik (vagy végtelen). Minden olyan görbe, aminek görbülete azonosan nulla, az egyenes. Könnyen ellenőrizhető az is, hogy a definíció alapján számított görbületi sugár a körnek a sugara és így görbülete ennek a reciproka. A definícióból látható, hogy G és az R nem lehet negatív.

A körnek a görbületi középpontja a kör középpontja. Tetszőleges görbe esetén a görbületi középpont a főnormális egyenesén, a görbe aktuális pontjától R távolságra található, a főnormális vektor irányában. Ez a pont a simuló sík egy pontja. Ezzel a középponttal és R görbületi sugárral rajzolt kör a görbe simuló köre (azaz a simuló kör a simulósíkban fekszik). A leírtak alapján nyilvánvaló, hogy ennek egyenlete:

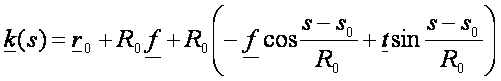
Ebben a felírásban az s a simuló körnek is ívhossz-paramétere lett.

A görbületet általános paraméter esetén a következőképpen határozható meg:

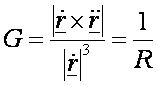
Torzió

Mielőtt a torziót definiálnánk, nézzük meg kicsit jobban a síkbeli görbéket. Síkgörbék esetén a simuló sík maga a görbe síkja. Az érintővektor és a főnormális (ha létezik) mindig a görbe síkjában marad. Ebből az adódik, hogy a binormális (ha létezik) mindig a görbe síkjára merőleges, azaz önmagával mindig párhuzamos, így mint helyvektor állandó. Ábrázoljuk, aztán elemezzük egy kicsit a következő síkbeli görbét:

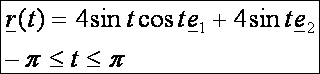
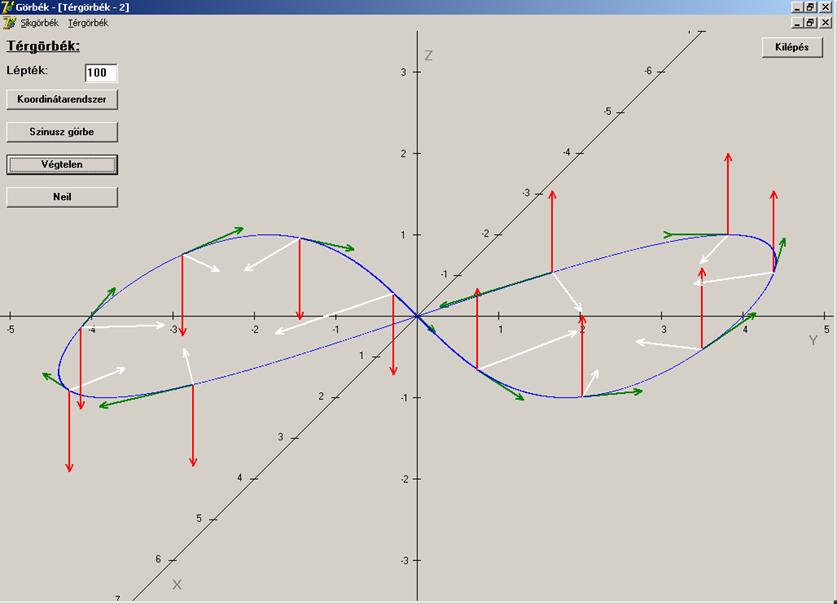
A képernyőn a kék vonal a fenti görbe, mely az (x, y) síkban fekszik, ezáltal ez a simulósíkja. Alakja eléggé hasonlít egy Lemniszkátára, de nem az. Inkább azt mondanám, hogy a végtelen jelet formázza. A görbe 12 pontjában látható a görbe kísérő triédere. A zöld vektorok az érintővektorok, a fehérek a főnormálisok (e kettő az (x, y) síkban fekszik) és a binormálisok a piros vektorok. A főnormálisok természetesen mindig a görbe belseje felé mutatnak. Ha a görbén az érintővektorok szerint végigmegyünk, akkor a főnormális az origóban (mely a görbe inflexiós pontja és kettős pontja) oldalt vált. Ebből az adódik, hogy pozitív y értékekre a binormális vektorok a z tengely pozitív irányába, negatív y értékekre a z tengely negatív irányába mutatnak. Vajon mi történik az origóban? Nézzük a deriváltakat:

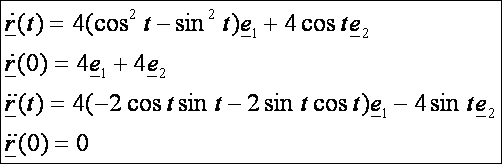
Az origóban a görbe két ága 90 fokos szögben metszi egymást (első derivált). Mivel a második derivált a t = 0 pontban nulla, így itt nincs görbülete, nincs főnormálisa és így nincs binormálisa sem.

A fenti görbe esetén a binormális vektorok szakaszonként állandók, azt mondhatjuk, hogy a síkgörbék nem csavarodnak. Térgörbék esetén ez már nem feltétlen van így. A simulósík nem állandó, így a binormális sem. A binormális változását, pontosabban változási sebességének nagyságát (szögsebességét) a görbe torziójának nevezzük és T -vel jelöljük:

Ha a kísérő triédert az érintővektorral szembe fordulva nézzük, akkor a binormális elfordulása kétféle lehet. Ha az elfordulás az óra járásával ellentétes irányú, akkor a torzió pozitív, ha megegyező, akkor negatív előjelű. Ilyen előjelválasztással élve a torzió:

Azaz a torzió a binormális ívhossz szerinti deriváltjában a főnormális mellett fellépő együttható negatívja. A torzió ívhossz-paraméterben a következőképpen számíthatjuk ki:

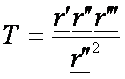
A torzió általános paraméter esetén a következőképpen határozható meg:

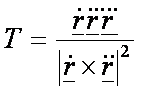
Teljes görbület, Frenet képletek

A görbe egy adott pontjához tartozó vektort a teljes görbület vektorának, vagy Darboux-vektornak nevezzük. Ennek hosszát, a:

számot teljes görbületnek (vagy Lancret-féle görbületnek) nevezzük.

Írjuk fel egy görbe adott pontjához tartozó kísérő triéder vektorainak ívhossz szerinti deriváltjait magában a kísérő triéderben:

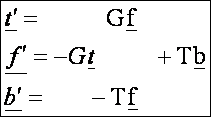
Ezeket a vektoregyenleteket Frenet képleteknek nevezzük. A Frenet formulák a Darboux-vektorral is leírhatók:

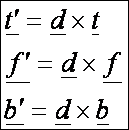
(Csak halkan jegyezném meg, hogy ez olyan, mintha a Darboux-vektor formailag átvenné a deriválás szerepét.)

Ha felírjuk egy görbe görbületét és torzióját az ívhossz függvényében, akkor a görbe természetes egyenleteihez jutunk. Ugyanis e két függvény egy mozgástól eltekintve egyértelműen meghatározza a térgörbét. Másképpen fogalmazva: ha két térgörbe görbülete és torziója pontról-pontra megegyezik, akkor azok mozgással fedésbe hozhatók. Ez azt jelenti, hogy a görbület és a torzió a görbe két invariánsa. De a görbe minden további invariánsát is meghatározzák, ezért a görbület és a torzió invariáns bázist alkot.

Ez utóbbiaknak van egy érdekes folyománya: annak szükséges és elégséges feltétele, hogy egy görbe önmagában eltolható legyen az, hogy: G = konstans és T = konstans legyen. Ilyen görbe viszont csak egyetlen egy van, ez pedig a közönséges csavarvonal.

Ennek a görbülete és torziója viszont konstans:

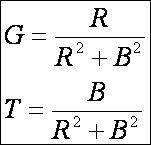
A közönséges csavarvonal G = 0 (azaz ) esetén egyenessé, T = 0 (vagyis B = 0) esetén pedig körré fajul. (Így az egyenes és a kör is önmagukban eltolhatók.)

A térgörbe vetületei a kísérő háromél síkjaiban

Nagyon tanulságos lehet megvizsgálni, hogy milyen görbéket kapunk, ha a görbének meghatározzuk a kísérő triéder síkjaira vonatkozó vetületeit. Ezek a vetületi görbék egy adott pont környezetében jellemzik a görbe viselkedését. Mindegyik vetület bizonyos értelemben csak közelíti a görbét, minél kisebb környezetre szorítkozunk, annál jobban.

A keresett vetületek egyenletének levezetését, mely Taylor-sorfejtésen alapul, most és itt nem írnám le, csak az eredményeket.

A simuló síkra vonatkozó vetület közelítő egyenlete:

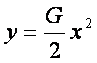
Ez egy közönséges parabola.

A normálsíkbeli közelítés:

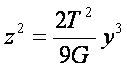
Ezt Neil-féle parabolának nevezzük.

A rektifikáló síkbeli közelítés pedig:

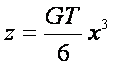
Ez egy harmadrendű parabola.

A képletekben a G a görbe görbülete, T pedig a torziója abban a pontban, ahová a lokális koordinátarendszert (kísérő triédert) felvettük. Ezek a görbék így néznek ki:

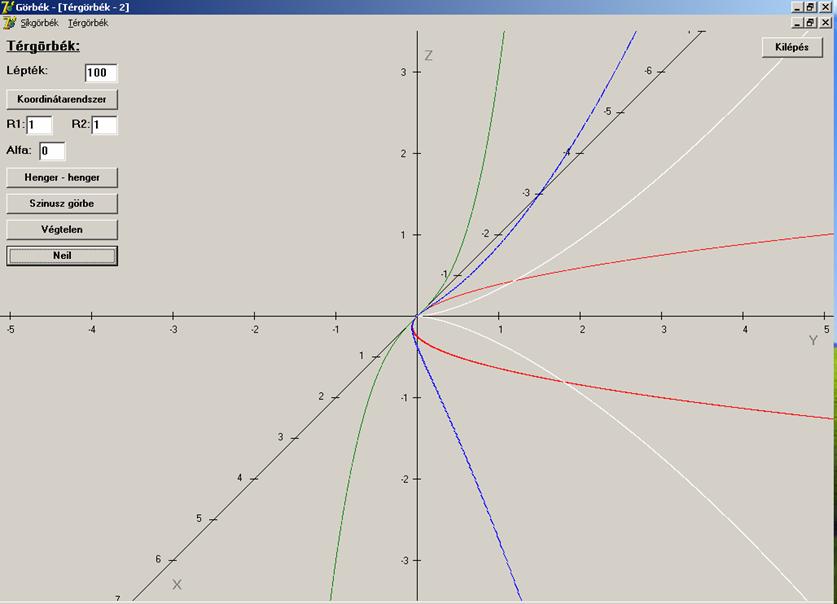
A rajzon a térgörbe kék színű, amely átmegy az origón, és érintője az x tengely. Ebben a pontban rajzoltuk fel a kísérő triéder síkjaira eső vetületeit. A koordinátasíkok és a vetületek:

(x, y) a simulósík, és benne a parabola piros színnel.

(y, z) a normálsík, és benne a Neil-féle parabola fehér színnel.

(x, z) a rektifikáló sík, és benne a harmadrendű parabola zöld színnel.

A vetületek arra világítanak rá, hogy a térgörbe elsősorban (lineáris megközelítésben) az érintő egyenesén fekszik, második (magasabb rendű) megközelítésben a simuló síkon és csak harmadrendű megközelítésben lép ki ebből a síkból (a Neil parabola szerint).

Megfigyelhetjük, hogy sem a görbének, sem a vetületeknek nincs olyan pontja, amelynek y koordinátája negatív lenne. Ez azt jelenti, hogy a görbék egyike sem lép át az (x, z) síkon. Felvetődhetne, hogy miért ilyet és nem olyat rajzoltunk, amelyek átlépnek? Csak azért, hogy ezek a görbék olyanok legyenek, amilyenek a szakirodalomban találhatók? Vagy van komolyabb indok is? Igen, van. Nézzük meg jobban a rektifikáló síkot, milyen a viszonya a görbéhez. Hát ez bizony érinti a görbét. Akkor miért nem nevezik érintő síknak? Hát azért nem, mert érintő mivolta őt nem határozza meg egyértelműen. Nem túl precízen fogalmazva: ha ezt a síkot elég kis szöggel az x tengely körül elforgatjuk, akkor még mindig egy közös pontja lesz a görbével, és még mindig a görbe az egyik oldalára esik. Azaz, ekkor is érintő síkot kapunk. Helyzetét tehát a görbe nem közvetlenül határozza meg, hanem a főnormálison keresztül, hiszen erre a vektorra merőleges. (Megjegyezném, hogy a felületeknél ilyen probléma nincs: ahol létezik érintő sík, ott egyértelmű is.) Természetesen van olyan görbe is, amely a kiszemelt pontunkban átlépi az (x, z) síkot. De ekkor az x tengely nem érintő, hanem érint és metsz, vagyis a görbének itt inflexiós pontja van. De ekkor a második derivált eltűnik, nincs főnormális, és nincs kísérő triéder. Hát ezért nem lépi át a görbe az (x, z) síkot, mert az ilyen pontokban, ebben a témakörben, nem vizsgálódhatunk.

Következő lap: http://gorbem.hu/MT/DiffGeom5.htm