Differenciálgeometria (2)

Vektorok és vektor-függvények

A háromdimenziós Euklideszi térben legyen adva egy Descartes-féle derékszögű koordinátarendszer. Ekkor a tér P pontjába mutató r helyvektorát a következő alakban írhatjuk fel:

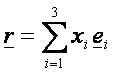
ahol az e_i a koordinátarendszer egységnyi hosszúságú bázisvektorai, x_i pedig az r vektor (vagy a P pont) adott bázisra vonatkozó koordinátái. Alkalmazzuk a továbbiakban az Einsten-féle konvenciót: amennyiben egy kifejezés egy tagjában kétszer fordul elő egy latin index, akkor arra 1 -től 3 -ig összegzést kell végrehajtani, azaz az egyszerűbb írásmód:

Mivel a bázisunk ortonormált, a bázisvektorok szorzata a Kronecker szimbólummal fejezhető ki:

Vegyük észre, hogy itt a latin indexek egy tagon belül nem ismétlődnek, tehát összegzést nem jelentenek. Ebben az esetben viszont értékük 1 -től 3 -ig bármi lehet. Ez az egyenlet tehát összesen 9 egyenlőséget takar. A Kronecker delta értéke:

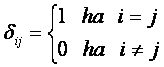
ami mátrixként felfogva a harmadrendű egységmátrix.

A közönséges egyváltozós valós függvényeket skalár-függvénynek nevezzük. Ha az r vektor értéke egy t skalártól függ, akkor vektor-skalár függvényről beszélünk. Formailag:

Tartalmilag ez három skalár koordinátafüggvényt: x_i(t) jelent. Elképzelhető, hogy egy függvény értékkészlete skalár és a függő változó vektor, ekkor skalár-vektor függvényről, ha pedig a függő és független változó is vektor, akkor vektor-vektor függvényről beszélünk. A skalár-vektor függvény geometriai megfelelője a térgörbe, a két skaláris változó vektorfüggvényének a felület, a vektorváltozó skalár-függvényének a skaláris mező, a vektorváltozó vektorfüggvényének a vektormező a geometriai megfelelője.

Mindegyik vektorfüggvény típusnál a koordináták leírása skalár-függvényekkel történik. Így elég természetes módon visszavezethető a vektor értékű függvények analízise a valós függvényekre. Egy r(t) vektor-skalár függvény akkor folytonos, ha koordinátafüggvényei folytonosak. Egy r(t) vektor-skalár függvény az értelmezési tartománya egy t₀ pontjában deriválható, ha a koordinátafüggvényei deriválhatók a t₀ pontban. A derivált egy vektor, melynek koordinátái a koordinátafüggvények deriváltjai:

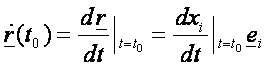
Az általános paraméter (t) szerinti deriváltat felül-ponttal fogjuk jelölni. Ha a vektor-skalár függvény értelmezési tartománya minden pontjában deriválható, akkor deriválhatónak mondjuk, és a derivált vektor-skalár függvényét -vel, vagy röviden -al jelöljük.

A görbe és előállítása

Definíció: Egy görbén olyan alakzatot értünk az Euklideszi térben, mely előállítható egy I intervallumon értelmezett r(t) vektor-skalár függvény helyvektorainak végpontjaiként (hodográfjaként), ha az r(t) leképezés kölcsönösen egyértelmű (azaz invertálható), minkét irányban folytonos, folytonosan deriválható és a differenciálhányadosa sehol sem null-vektor.

Néhány görbe vektor-skalár (szokás vektor-paraméteresnek és ha koordinátánként külön leírjuk, akkor paraméteres egyenletrendszernek is nevezni) előállítása:

a) (egy egyenes, ahol az egyenes egy pontja, pedig az irányvektora)

b) (egy kör, ahol a kör középpontja, R a sugara, síkja pedig az egymásra merőleges egységvektorok által van felfeszítve)

c) (egy tengelyű hengeres csavarvonal, ahol R>0 a henger sugara, az emelkedése)

d) (egy tengelyű egyszerű kúpos csavarvonal, ahol az emelkedése)

Minden, a feltételeknek eleget tevő r(t) függvény egyértelműen előállít egy görbét, de fordítva az egyértelműség nem áll fenn. Azaz, ugyanazon görbének lehet több, különböző paraméteres előállítása. Ha egy másik paraméterre szeretnénk áttérni a t -ről, mondjuk -ra, akkor meg kell vizsgálni a két paraméter kapcsolatát. Írja le a kapcsolatukat a leképezés. Ekkor a leképezésnek ugyanolyan tulajdonságokkal kell rendelkeznie, mint az r(t) -nek (azaz: invertálható, mindkét irányban folytonos, folytonosan differenciálható és a deriváltja nem lehet nulla). Ekkor az ilyen -t megengedett paraméter-transzformációnak nevezzük. Egy másik megengedett paraméterre való áttérés formailag az r(t) képletében a helyettesítéssel valósítható meg: . Nézünk erre egy példát. Legyen:

Hajtsunk végre ezen a görbén egy , nyilvánvalóan megengedett paraméter-transzformációt. Ekkor: . Ezt behelyettesítve:

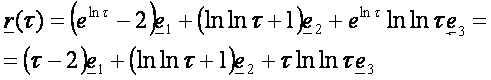
Ha az r(t) görbe pontjain a t növekedő értékein keresztül megyünk végig, akkor ez egy haladási irányt, vagy orientációt határoz meg a görbén. A akkor adja a görbén ugyanazt az orientációt, ha a szigorúan monoton növekvő függvény. Ha a szigorúan monoton csökkenő, akkor ellentétes irányú orientációt kapunk. Egy görbének tehát csak két orientációja létezik.

Ha egy görbe pontjai egy síkra illeszkednek, akkor azt mondjuk, hogy a görbe síkgörbe, ellenkező esetben térgörbe.

Síkgörbék ábrázolása

Ha a görbéket paraméteres egyenletrendszerrel adjuk meg (vektor-skalár függvény koordinátái külön egyenletekkel leírva), akkor könnyen ábrázolhatjuk őket, hiszen a görbéhez tartozó pontok mindegyik koordinátája egy paraméterrel van előállítva. Szokás ezért ezt a megadási módot explicit megadási módnak is nevezni. Abban az esetben, ha görbéket koordinátafüggvényei közötti kapcsolattal írjuk le (az x, y és z koordinátákkal), akkor ezt implicit alak nevezzük. Ezek az egyenletek gyakran (de nem mindig) könnyen átalakíthatók explicitté, ha sikerül az egyik koordinátát a többivel kifejezni, például: z = f(x, y) alakban. Számos, neves sík- és térgörbét ismerünk. Először ilyen síkgörbéket ábrázolok egy programmal. Kezdjük néhány egyszerűbbel. Az egyszerűség kedvéért az r két koordinátáját x és y -nal jelöljük:

Egyenes ( – olajzöld ):

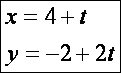
Kör ( – kék):

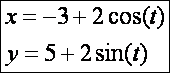
Ellipszis ( – vörös):

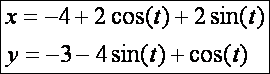
Kardioid ( – zöld):

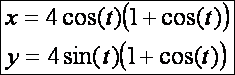
Descartes-levél ( – fekete, asszimptotája fehér):

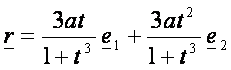
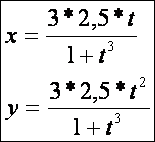
A következő sreenshot-on csak cikloisokat látunk. A ciklois paraméteres egyenletrendszere ():

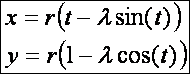
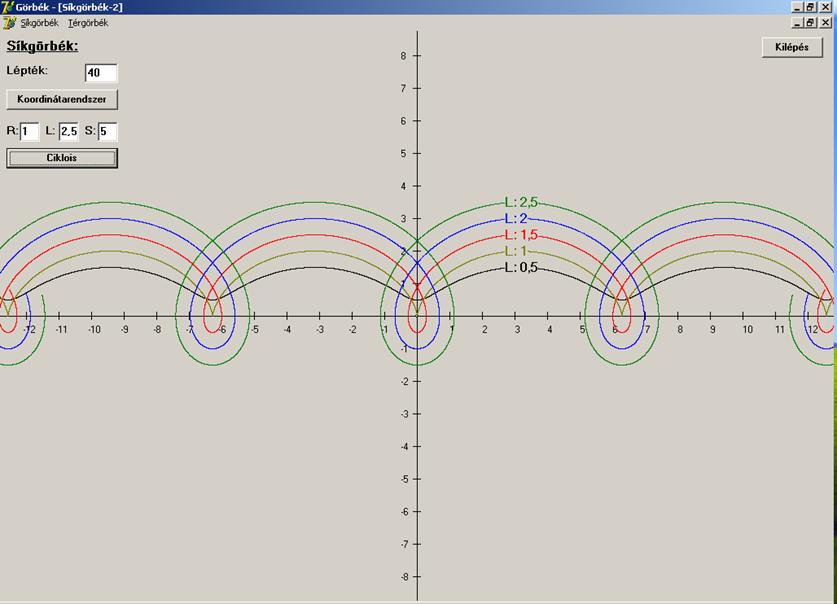
A görbe alakját a határozza meg. Ha értéke nagyobb mint 1, akkor hurkolt, ha kisebb mint 1, akkor nyújtott lesz, ha pedig az értéke 1, akkor csúcspontokkal rendelkezik a ciklois. Az R értéke mindig 1, az értékei pedig: 0.5, 1, 1.5, 2 és 2.5, ahogy az a grafikonon látható.

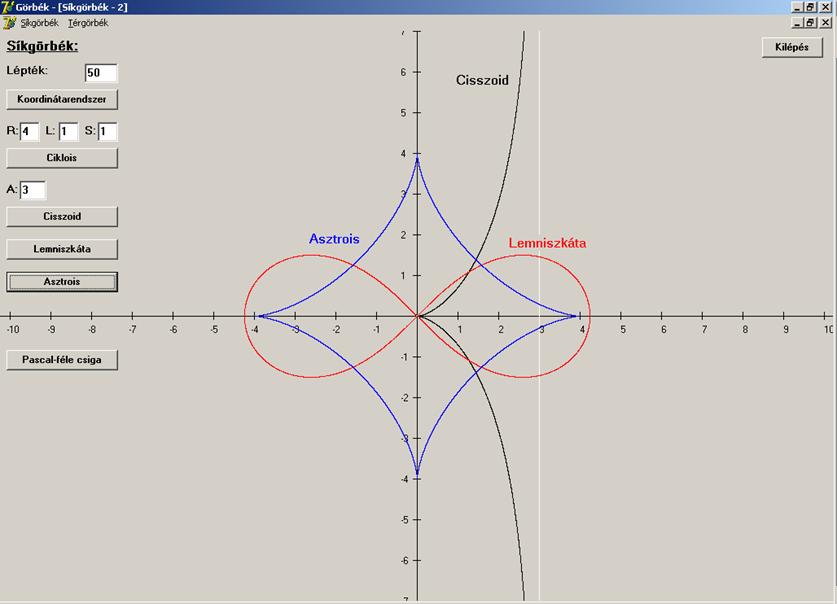
A következő képernyőn három görbét találunk:

Cisszoid ( – fekete, asszimptotája fehér):

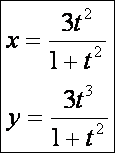
Lemniszkáta ( – vörös):

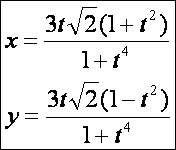
Asztrois ( – kék):

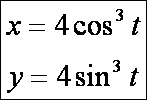
A következő képernyőn csak Pascal-féle csigákat találunk, melynek paraméteres egyenletrendszere () :

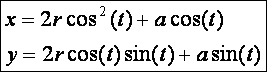
A görbe alakját az r és az a viszonya határozza meg. Az ábrázolt görbék esetén mindig r=1, az a értéke pedig 0.5, 1, 2, 3, 4 és 5. Ha 0<a<2r, akkor a görbe hurkolt, ha 2r<a<4r, akkor nem hurkolt de két inflexiós pontja van, ha a>=4r, akkor konvex az alakja. Ha a=2r, akkor a görbe egy szívgörbe (kardioid).

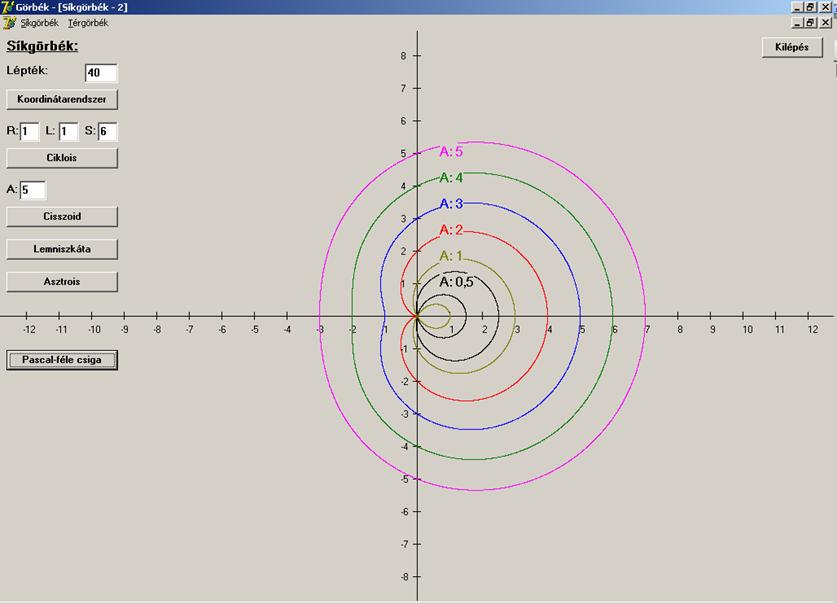
A következő képernyőn két spirálgörbe látható:

Archimédesi spirál ( – fekete):

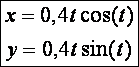
Hiperbolikus spirál ( – kék, asszimptotája fehér ):

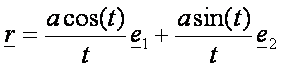
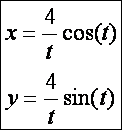
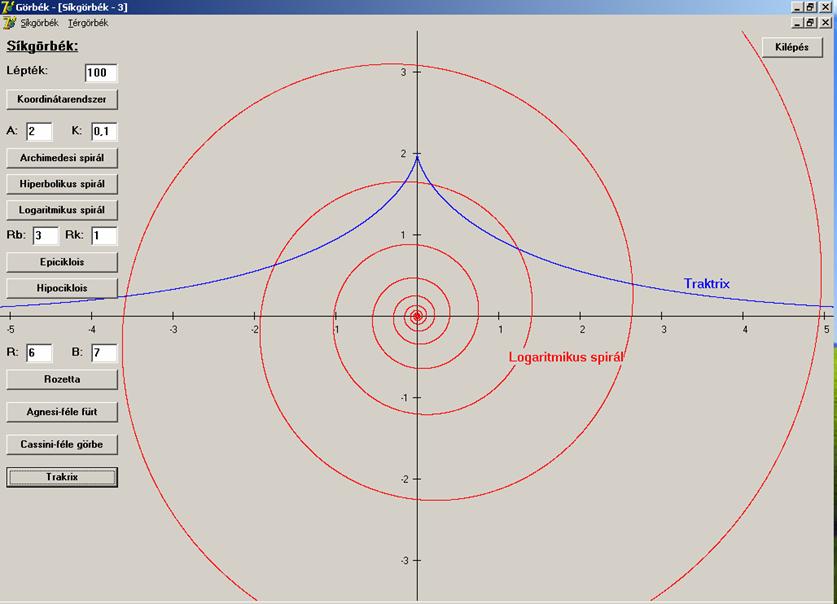
Az előző képernyőnek a folytatása, ismét egy spirál (de az előzőn már zavaró lett volna) és a trakrix, amely egy vontatási görbe (ha egy pontszerű testet egy fonállal egy olyan egyenes mentén húzunk, mely egyenesen nincs rajta a pont, akkor a pontszerű test egy traktrix mentén mozog):

Logaritmikus spirál ( – vörös):

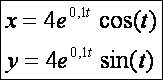
Traktrix ( – kék):

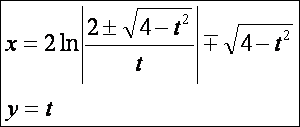
A következő képernyőn ciklois (körnek körön való gördülésével előálló) görbék láthatók:

Epiciklois ( – zöld, tartógörbe kör, ami fehér):

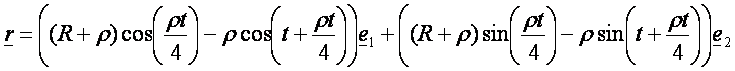
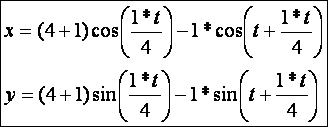
Hipociklois ( – vörös, tartógörbe kör, ami fehér):

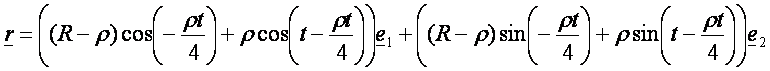
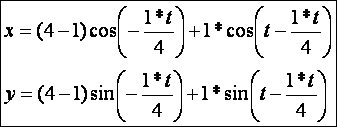
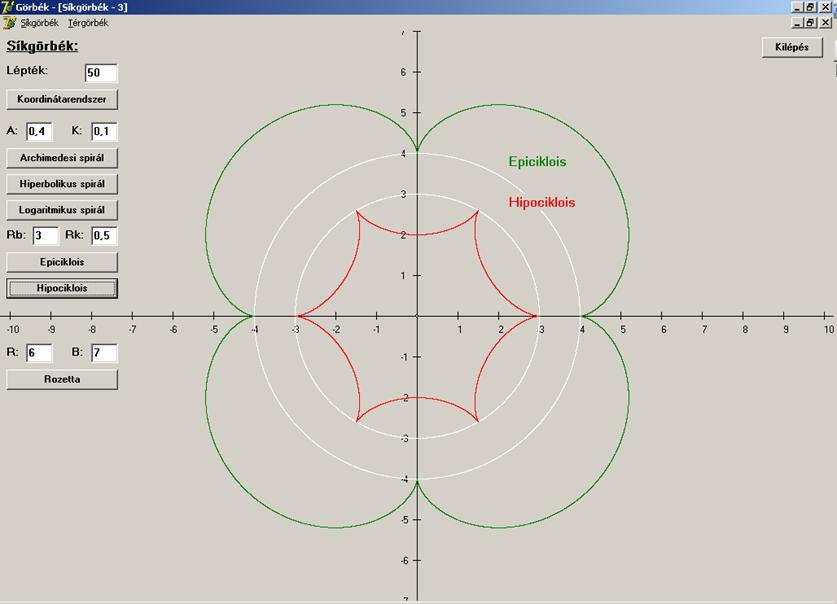
A most ábrázolt síkgörbénk a rozetta (rózsa):

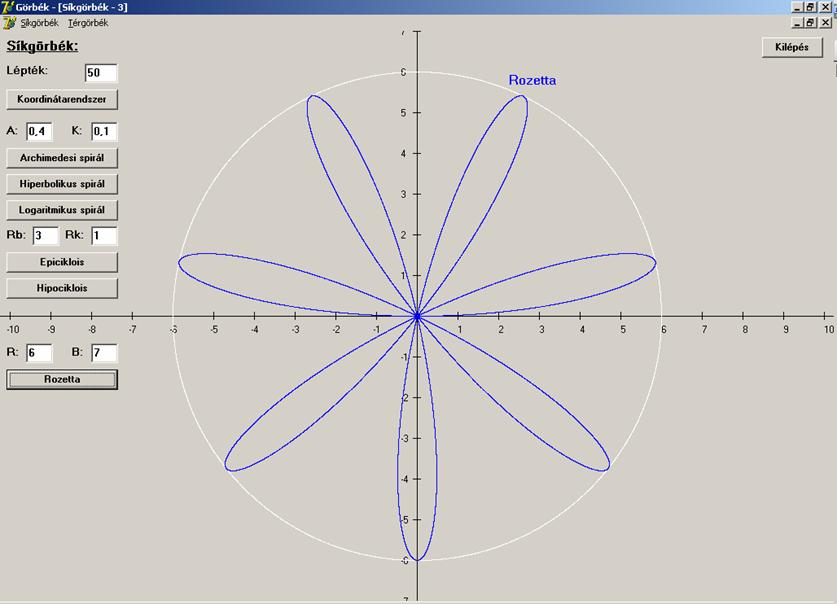
Rozetta ( – kék, tartógörbe kör, ami fehér)

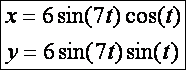
Még egy görbe:

Agnesi-féle fürt ( – kék, tartógörbe kör, ami fehér):

.

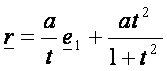
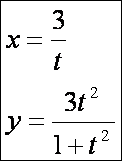
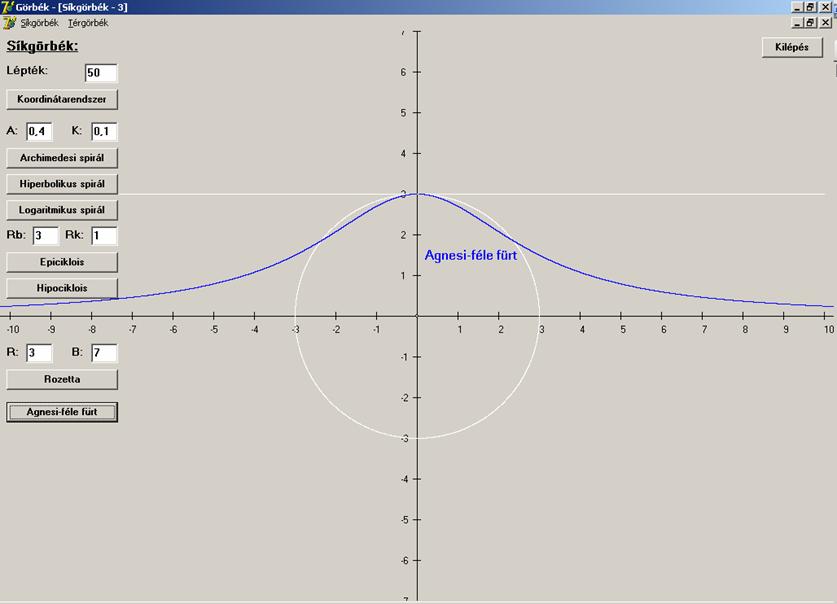
Most a Cassini-féle görbét ábrázoljuk. Definíció szerint ez azon pontok mértani helye a síkban, amelyeknek a sík két pontjától (fókuszoktól) mért távolságának szorzata állandó. Ez alapján, ha a szorzatot b²-el jelöljük, akkor a következő egyenletekhez jutunk:

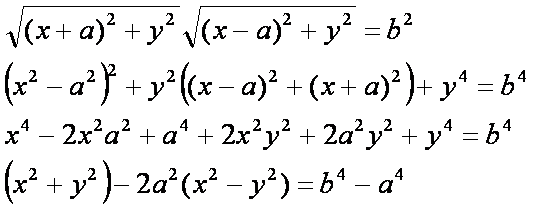
Ez utóbbi könnyen átírható polár-koordinátára. Mivel

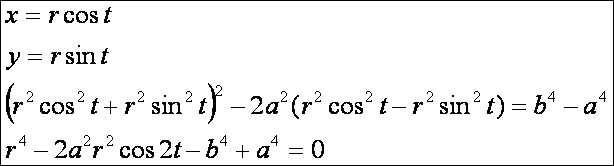
Ha bevezetjük a 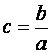jelölést, akkor a görbe lehetséges alakját a c segítségével könnyen megfogalmazhatjuk:

Ha , akkor a görbe alakja ovális.

Ha , akkor a görbe egy négy inflexiós ponttal rendelkező, zárt görbe.

Ha , akkor lemniszkáta az alakja.

Ha , akkor két független ovális görbére esik szét.

Ha , akkor a két fókuszponttá zsugorodik.

Íme néhány Cassini-féle görbe. A görbék mellé írt számok a szakaszok hosszának a szorzatát jelentik:

További két görbét ábrázolunk.

Sztrofoid( – kék) :

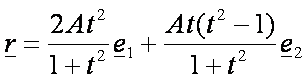
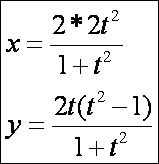
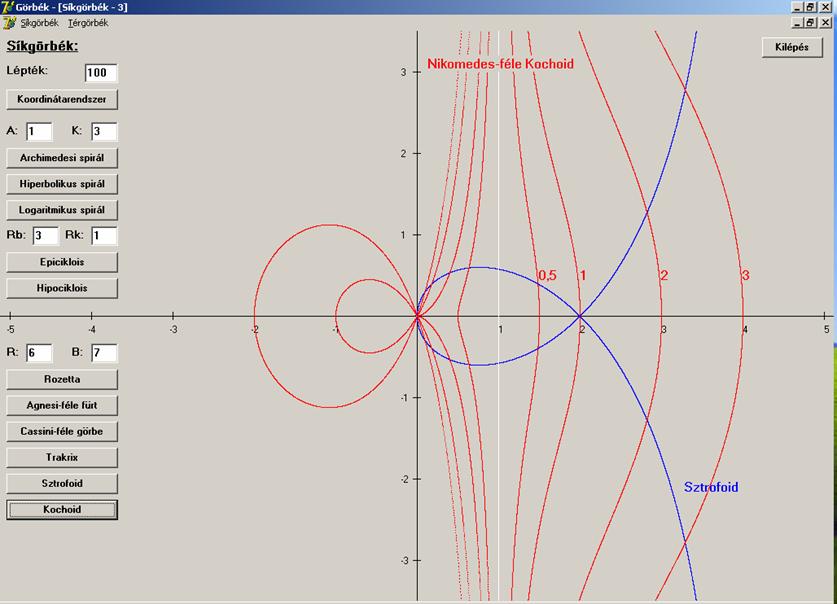
Kochoid: ha a síkgörbe pontjaihoz tartozó vektorokat egy állandó a hosszúságú szakasszal növeljük és csökkentjük, akkor az adott görbéhez tartozó kochoidot kapunk. Ha a görbe egyenlete akkor a kochoidjának egyenlete: . Most Nikomedes-féle kochoidot ábrázoljuk, mely az egyeneshez tartozó kochoid. Ennek alakja nagyban függ az a értékétől.

esetén az origó izolált pont, a görbének két egyszerű ága van (pl.: a = 0,5).

esetén az origó visszatérő pont és egyben csúcspont (a = 1).

esetén az origó csomópont, egy hurok jelenik meg a 3. és 4. síknegyedben (pl.: a = 2, a = 3).

Nikomedes-féle kochoid (– piros, az alap x = k egyenes fehér (k = 1), a számok az a értékét jelentik):

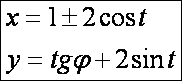
Következő lap: http://gorbem.hu/MT/DiffGeom3.htm