Differenciálgeometria (15)

A következőkben – a felület első és második alapmennyiségeinek birtokában – a felület alakjára, azaz a háromdimenziós Euklideszi térbe való beágyazásáról szeretnénk információkat kapni. Kíváncsiak leszünk a felület görbületére (pontosabban görbületeire), a felületek speciális görbéire, és főleg azokra közülük, amelyek a sík egyeneseinek felelnek meg. Célunk elérése csak több lépcsőben lehetséges. Mivel a görbék elméletében a görbe görbületével már foglalkoztunk, induljunk el innen. Nézzük meg, hogy egy felületi görbe görbülete hogyan függ az őt tartalmazó felület adataitól.

A felületi görbe görbülete

Legyen az felület felületi görbéje:

Legyen továbbá P₀ ennek a görbének egy pontja. Tegyük fel, hogy a görbe e pontbeli simulósíkja nem esik egybe a felület érintősíkjával, azaz a görbe f főnormálisa és a felület n normál-egységvektora nem merőleges egymásra. Eléggé nyilvánvaló, hogy az ezen a P₀ ponton átmenő felületi görbék görbülete nem vehet fel tetszőleges értékeket, hiszen a felület ennek valamilyen korlátot szab. Próbálkozzunk meg ennek a felületi görbének a G görbületét kifejezni a felület alapmennyiségeivel. Térjünk át a felületi görbén az ívhosszra, ami legyen s = s(t). A Frenet képlet szerint:

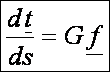
Tudjuk, hogy a görbe érintővektora:

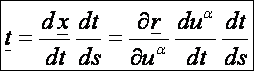
Vegyük ennek az ívhossz szerinti deriváltját:

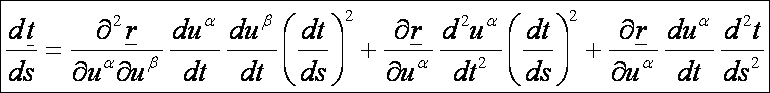
Szorozzuk meg mindkét oldalt skalárisan a felület normál-egységvektorával, és vegyük figyelembe, hogy a második és harmadik tag a felület érintősíkjában fekvő vektorok (skaláris szorzata az n -el eltűnik):

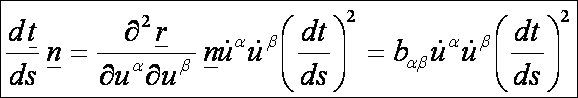
Tudjuk továbbá, hogy az inverz függvény differenciálási szabálya alapján:

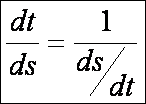
Ugyanakkor az első alapforma szerint:

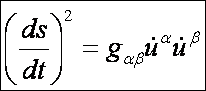
Vagyis:

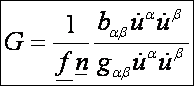
Újra megemlítve azt, hogy a görbe főnormálisa és felület normál-egységvektora nem merőlegesek egymásra.

Értelmezzük a kapott eredményt. Mivel a képletünk második tényezője az -nek nulladfokú homogén függvénye, annak értéke csak az érintő irányától függ. Azaz nem változik az értéke, ha az -t -val helyettesítjük. Az első tényező pedig csak f -től függ, hiszen az n a felület egy rögzített pontjára állandó. Azaz a felületi görbe görbülete csak az érintő irányától és a főnormális állásától függ (ha f és n nem merőlegesek).

Folytatva az elemzést: az x(t) görbe P₀ -beli simulósíkja a felületből egy síkgörbét vág ki, amelynek ugyanaz az érintője és a főnormálisa is, mint az x(t) -nek. Azaz egy felületi görbe görbülete megegyezik a simulósíkja által a felületből kimetszett görbe görbületével (természetesen, ha f és n nem merőlegesek). Ezért a felület egy adott pontjában megadott irányú és főnormálisú görbék közül elegendő az egyetlen ilyen síkgörbét vizsgálni, mert a többinek is ugyanaz a görbülete.

Nézzük meg mindezt egy rajzon. Fehér a felület, P₀ pedig a felület kiválasztott pontja. A sárga sík a pontbeli érintő sík, a kék sík a kék felületi görbe simulósíkja. A piros a kék és a zöld görbék a ponton átmenő felületi görbék. Az n a felület pontbeli normálvektora, a piros, a kék és a zöld vektorok a felületi görbék főnormálisai:

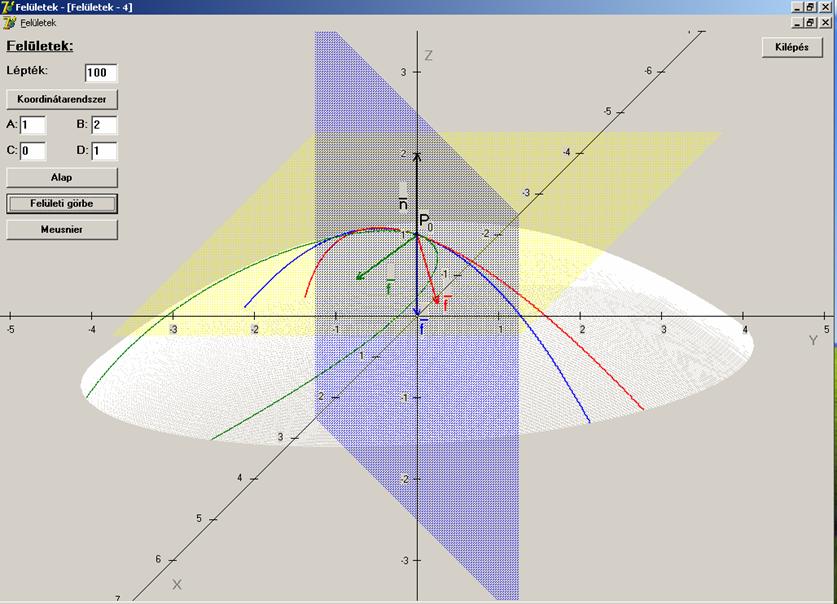
Nyilvánvalóan látszik a rajzból is, hogy minél jobban eltér a főnormális iránya a felület normálvektorának az irányától, annál nagyobb a felületi görbe görbülete (itt a zöld görbe görbülete a legnagyobb). A rajzon csak a kék felületi görbének a simulósíkja van feltüntetve. A kék felületi görbe speciális abban a vonatkozásban, hogy síkgörbe, azaz a simulósíkja önmagát metszi ki a felületből. Ez természetesen általában nincs így, a felületi görbe általában nem síkgörbe!

Példaként határozzuk meg a z = xy hiperbolikus paraboloid (1, 1) paraméterű pontján átmenő olyan felületi görbéjének a görbületét, melynek érintője és főnormálisa az a(2, -1, 4) vektorral párhuzamos. A hiperbolikus paraboloid paraméteres egyenletrendszere:

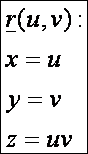
Az első alapmennyiségek:

A második alapmennyiségek (a DiffGeom14.htm lap alapján):

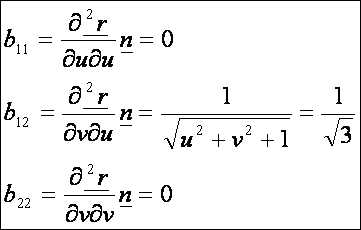
A görbe főnormálisa:

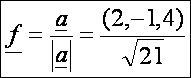
A felület normálvektora (a DiffGeom14.htm lap alapján):

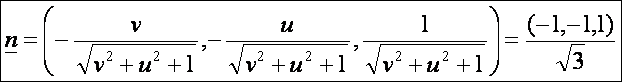
E két vektor skaláris szorzata:

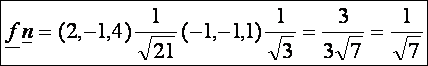
A felületi görbe görbülete:

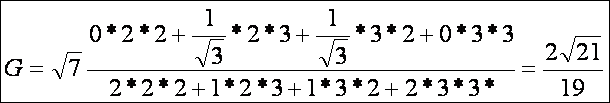
A fenti ábrához fűzött megjegyzés szerint a három felületi görbe görbülete különböző. Növekedő sorrendben: kék, piros és a legnagyobb görbületű a zöld. Ennek alapján feltehetjük a kérdést: vajon a felület adott pontján átmenő felületi görbék közül melyiknek a görbülete a legkisebb? Nyilvánvalóan annak a görbének, amelyre az fn szorzat eggyel egyenlő, azaz amikor a főnormális és a normálvektor párhuzamos. Bármely ilyen görbe görbülete egyenlő egy olyan síkgörbe görbületével, amelyet a görbe érintője és a felület normálvektora által felfeszített sík vág ki a felületből.

Meusnier tétel

Egy felületnek a normálvektorára illeszkedő síkokkal való metszésvonalait normálmetszeteknek nevezzük. A többi síkmetszetet szokás ferde metszetnek nevezni. A normálmetszet görbülete:

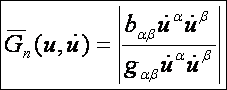
Tehát a normálmetszet görbülete a legkisebb az adott érintőjű síkmetszetek közül. Az ettől legfeljebb csak előjelben különböző

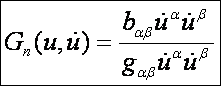
értéket az adott irányhoz tartozó normálgörbületnek nevezzük. A normálgörbület, melynek előjele lehet pozitív és negatív is, jobban jellemzi a felület görbületi viszonyait, mint a normálmetszet görbülete. Ezt jól példázza a hiperbolikus paraboloid esete. Ennek a felületnek bármely pontjában van olyan normálmetszet, ahol a főnormális és a felület normálvektora egyező, és olyan is, amely különböző irányú. Így a pontbeli normálgörbületek között van pozitív és negatív is.

Ha a főnormális és a felületi normál-egységvektor szögét -vel jelöljük, akkor a következők írhatók:

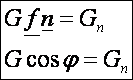
Ha az összefüggést a görbületek helyett a görbületi sugarakkal írjuk fel, ezt kapjuk:

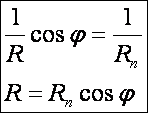
Ez utóbbi összefüggést Meusnier tételének nevezzük.

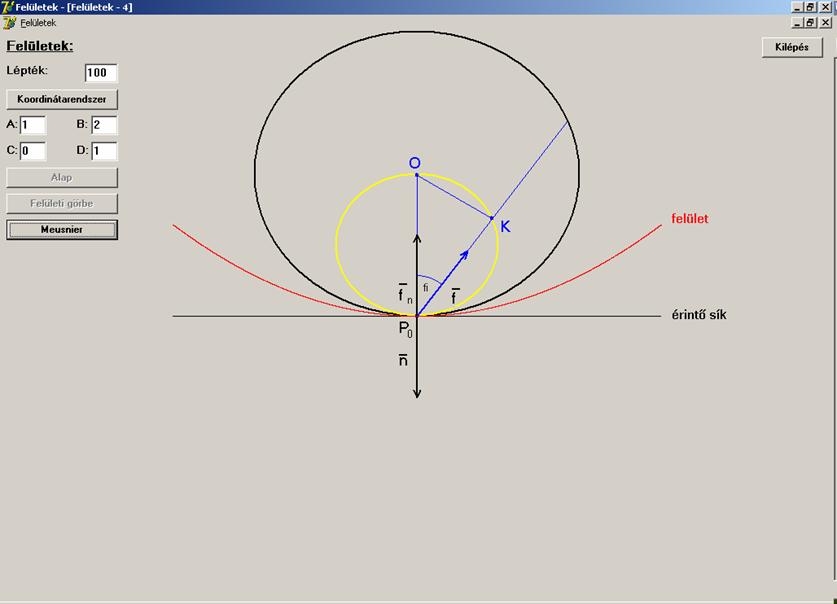
Vegyük fel a felületnek egy adott érintőirányra merőleges metszetét a P₀ pontban (így az érintővektor a rajz síkjára merőleges), melyet a következő ábrán láthatunk. Ezen a piros színű görbe a felület és a sík metszésvonala. A fekete színű egyenes az érintő síkot szemlélteti. A fekete kör az sugárral rajzolt gömb síkmetszete. Ekkor a Meusnier tétel geometriai jelentése az, hogy bármely, a P₀ ponton átmenő, adott érintőirányú felületi görbe simulósíkja ebből a felvett gömbből a görbe simulókörét metszi ki. Ezt a síkot az érintővektor és az f főnormális feszíti fel. A kimetszett simuló kör középpontját K jelöli. A sárga kör az összes lehetséges K helyét mutatja, amely egy átmérőjű kör (kivéve a P₀ pontot).

Most újra egy feladat következzen. Határozzuk meg a z = x² + y² forgásparaboloid egy pontjában annak a síkmetszetnek a görbületét, melynek síkja merőleges az illető ponton átmenő meridián görbére és a felületi normálissal Pi/4 szöget zár be. A forgásparaboloid paraméteres egyenletrendszere:

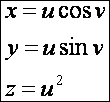
A forgásparaboloid pontja legyen az u = 1 és v = 1 paraméterértékekkel meghatározva. A forgásparaboloid első alapmennyiségei (DiffGeom11.htm alapján) az adott pontban:

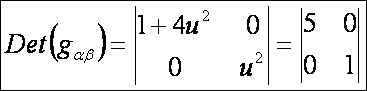
A forgásparaboloid második alapmennyiségei (DiffGeom14.htm alapján) az adott pontban:

Az fn szorzat értéke:

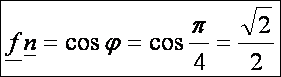
Mivel a görbe merőleges a meridián görbére:

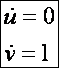
Így a felületi görbe görbülete:

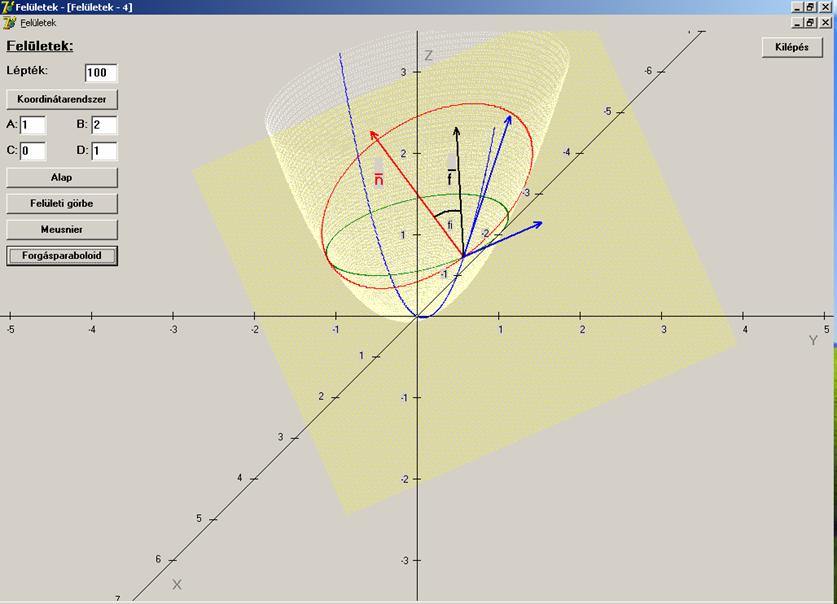
Mindez rajzban (fehér a paraboloid, sárga a metsző sík, kék parabola a meridián, kék vektorok a paramétervonal-érintők, piros vektor a felület normálvektora, fekete vektor a metszet görbe főnormálisa, piros a sík és a paraboloid metszésvonala):

Főnormálgörbületek, a Gauss és Minkowski féle görbületek

Már ennek a lapnak a bevezetőjében is utaltam rá, hogy a felületnek nincs olyan egyértelmű görbülete (speciális esetektől eltekintve) mint a görbéknek. A görbület a görbéhez kapcsolt fogalom. Már eddig is felületi görbék görbületeiről beszéltünk és nem a felület görbületéről. A továbblépés alapja most is a felületi görbék görbülete. Tekintsük a normálgörbületet. Ez a kiválasztott felületi pont mellett még a normálmetszet irányától is függ. Értéke két határ között mozog. Nem lehet akármekkora kicsi és nagy sem. Keressük meg a normálgörbület irány szerinti szélsőértékeit. A normálgörbület:

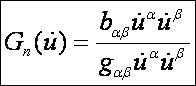
Mivel ez a függvény az pont kivételével folytonos és differenciálható, a szélsőérték létezésének feltétele a differenciálhányados eltűnése. Képezzük a deriváltat:

A középső tört első tagjában az első alapformával lehet egyszerűsíteni. A második tagban a második és az első alapforma hányadosa pedig G_n-el egyenlő. Így:

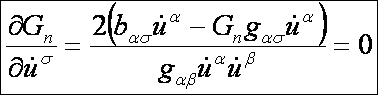
Vagyis a szélsőérték feltétele:

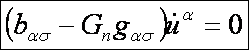
Ez két egyenletet jelent G_n-re nézve. Ennek a homogén egyenletrendszernek akkor létezik triviálistól különböző megoldása, ha a

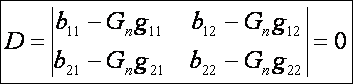
determináns eltűnik. A D -re egy másodfokú egyenletet kaptunk:

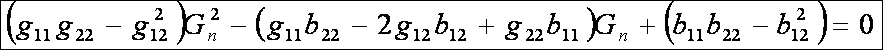
Legyen ennek a másodfokú egyenletnek G₁ és G₂ a két gyöke. Ezt a két görbületet főnormálgörbületnek nevezzük. Azokat az irányokat pedig, amelyekben ezek létrejönnek főirányoknak nevezzük.

A másodfokú egyenlet gyökök és együtthatók közötti összefüggései alapján:

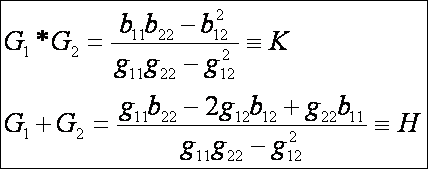
A K -t a felület szorzat, vagy Gauss-féle görbületének, a H -t pedig összeg, vagy Minkowski-féle görbületének nevezzük.

Felvetődhet a kérdés, vajon mi van akkor, ha a két előbbi görbület egyenlő (minimum és maximum azonos), amit jelöljünk G₀ -al. Ez akkor lehetséges, ha

azaz a felület első és második alapmennyiségei arányosak. Ekkor minden normálgörbület azonos, minden irány szélsőérték-irány. Ha G₀ nem nulla, akkor ez a gömbfelületre igaz. Ez azt jelenti, hogy a gömb egy konstans görbületű felület, amelynek minden normálmetszete egy főkör, és amelynek minden pontjában a Gauss görbülete, ahol R a gömb sugara. Egy tetszőleges felület azon pontjait, ahol a két főnormálgörbület egyenlő, gömbi pontoknak nevezzük. Az olyan gömbi pontokat, amelyekre G₀ = 0 igaz, síkpontoknak nevezzük. A sík minden pontja ilyen pont. Nyilvánvaló, hogy ebben az esetben a második alapmennyiségek mindegyike 0. Megjegyezzük még, hogy ha G₁ <> G₂, akkor az ezeknek megfelelő irányok egymásra merőlegesek.

A gömb főnormálgörbületei

A fentiek alapján szükségünk van a gömb alapmennyiségeire. Az első alapmennyiségek:

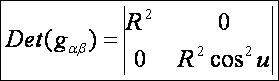
A második alapmennyiségek:

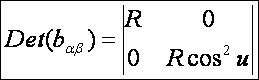
Ezek alapján a főnormálgörbületek:

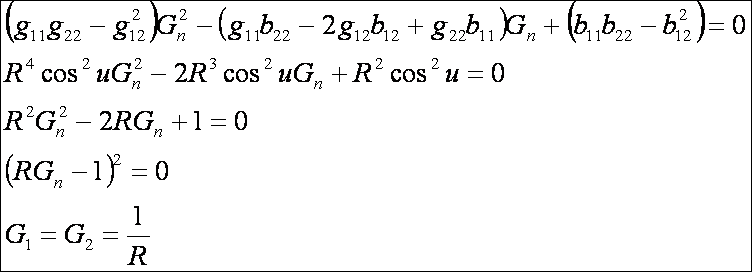
A henger főnormálgörbületei

Az első alapmennyiségek:

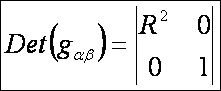
A második alapmennyiségek:

Ezek alapján a főnormálgörbületek:

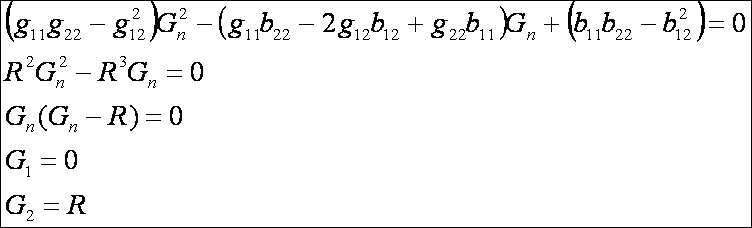
Ez az eredmény számomra meglepő. Én jobban örültem volna, ha a G₂ nem R lenne, hanem az R -nek a reciprokával lenne kapcsolatos. Ennek ellenére a levezetésekben sehol sem találtam hibát, tehát el kell fogadnom. A henger Gauss görbülete 0, ami a továbbiakban még fontos lehet.

A kúp főnormálgörbületei

Az első alapmennyiségek:

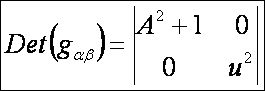
A második alapmennyiségek:

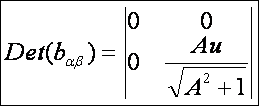
Ezek alapján a főnormálgörbületek:

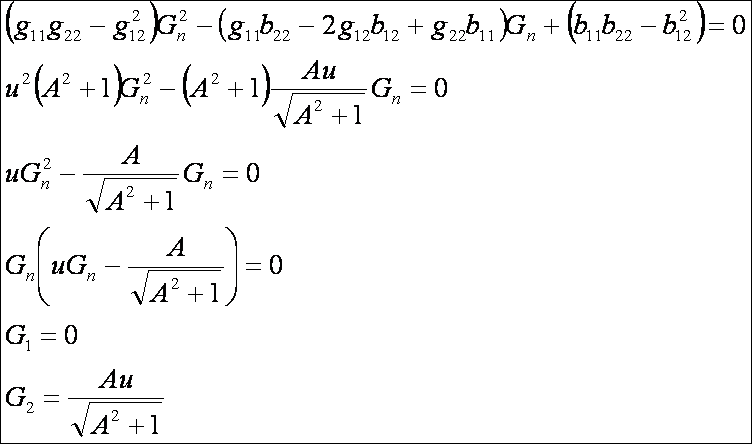
A kúpnak is 0 a Gauss görbülete.

A hiperbolikus paraboloid főnormálgörbületei

Az első alapmennyiségek:

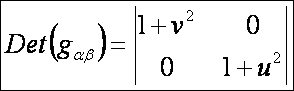
A második alapmennyiségek:

Ezek alapján a főnormálgörbületek:

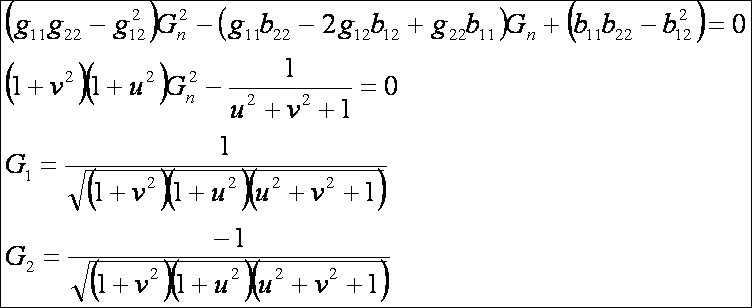
E lap fentebbi részén hivatkoztunk erre az eredményre. Mint látható a hiperbolikus paraboloid két főnormálgörbülete különböző előjelű, azaz a normálgörbületek között is vannak különböző előjelűek. Látható továbbá az is, hogy ennek a felületnek a Minkovszki görbülete nulla.

Euler tétele

Legyen egy felület kiválasztott pontjában a G egy tetszőleges irányhoz tartozó normálgörbület. Legyen ugyanitt G₁ és G₂ a főnormálgörbületek (melyekhez tartozó irányok egymásra merőlegesek), legyen továbbá a G és a G₁ iránya által bezárt szög. Ekkor:

Ezt az igen egyszerű összefüggést Euler tételének nevezzük. Ezzel a felületi görbületekkel kapcsolatos elemzésünk végére érkeztünk. Megállapíthatjuk, hogy a felületnek nincs a görbékhez hasonló görbülete (egy érték, kivétel a gömb és a sík esetét). Viszont az egy ponton átmenő felületi görbék görbületét a fenti képlet segítségével nagyon egyszerűen meghatározhatjuk.

Euler tételének alkalmazásaként határozzuk meg a z = xy hiperbolikus paraboloid pontjaiban az eltűnő normálgörbületek irányát:

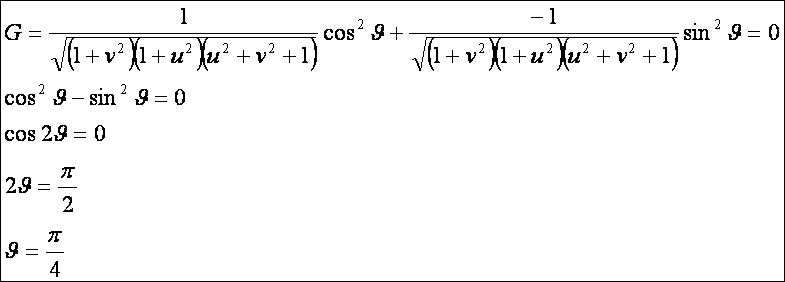
Azaz a nulla normálgörbületi irányok 45 fokos szöget zárnak be egymással. Másképp fogalmazva, a felület minden pontján átmegy két olyan egyenes, amelyek 45 fokos szöget zárnak be egymással.

A Dupin-féle indikátrix

Már a gömbi- és a síkpontok fogalmával is azt érzékeltettük (egy speciális esetben), hogy vajon a felület miként viselkedik egy pontja környezetében. Lokálisan gömbi pont esetén a gömbhöz, síkpont esetén a síkhoz hasonló az alakja. Ebben a részben, a pont környezetében való viselkedésre további megállapításokat fogunk tenni.

Ha az

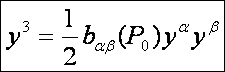
oszkuláló paraboloidot (amely vagy elliptikus paraboloid, vagy hiperbolikus paraboloid, esetleg elfajuló parabolikus henger) olyan koordinátarendszerben írjuk fel, ahol a felületi paramétervonal-érintők a főirányokba mutatnak (a sík esetén ez nem valósítható meg, ezért a vizsgálatainkból ezt most kizárjuk), akkor (mivel az Euler tétel miatt), a következőt kapjuk:

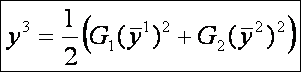
ahol ebben az új koordinátarendszerbeli általános koordináták. Ez azt mutatja, hogy az oszkuláló paraboloidot már főnormálgörbületek meghatározzák. Az oszkuláló paraboloidnak a felület egy pontjában lévő érintősíktól távolságra lévő síkokkal alkotott metszeteinek az érintősíkra vett merőleges vetületeit a felület adott pontbeli Dupin-féle indikátrixának nevezzük. Ennek egyenlete:

Így a Dupin-féle indikátrix típusát már a felület pontbeli Gauss görbületéből meg tudjuk határozni. Nevezetesen: a Dupin-féle indikátrix aszerint ellipszis, hiperbola vagy elfajuló egyenes-pár, amint a Gauss-féle görbület pozití, negatív vagy nulla.

Az oszkuláló paraboloid eredeti egyenletéből is felírható a Dupin-féle indikátrix egyenlete:

Ez pedig aszerint ellipszis, hiperbola vagy elfajult egyenes-pár, miszerint a második alapmennyiségek determinánsa pozitív, negatív vagy nulla. Egy felület adott pontját a pontbeli Dupin-féle indiátrix alakjától függően, (praktikusan a második alapmennyiségek determinánsának előjele alapján) elliptikus, hiperbolikus illetve parabolikus pontoknak nevezzük.

A háromféle indikátrixot egy ábrán ábrázoltuk. A piros színű ellipszis, a kék színű a két hiperbola, melyből az egyik a 0.5 a másik a -0.5 értékből adódik (a közös asszimptóták a fekete színű egyenesek), és zöld színnel az elfajuló egyenes-párt láthatjuk.

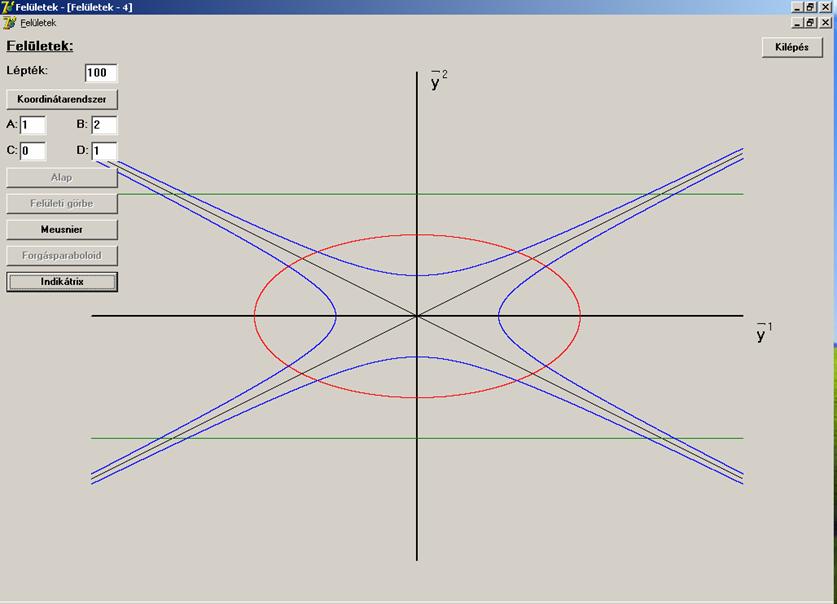
A következő ábrákon az oszkuláló paraboloid lehetséges eseteit látjuk a Dupin-féle indikátrixot adó metszetekkel együtt. Az elsőn elliptikus paraboloidot (fehér) és a kék ellipszist, ami a z = 0.5 síkkal való metszete.

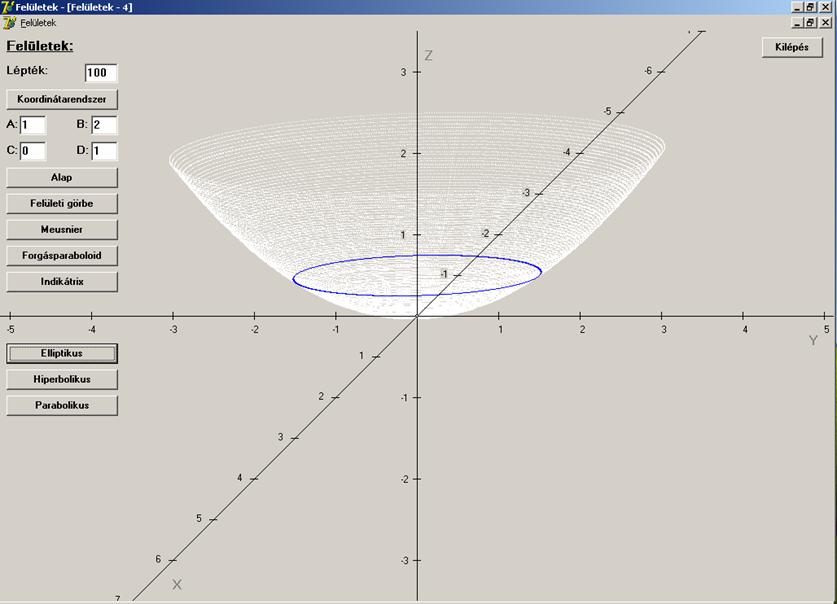
A másodikon hiperbolikus paraboloidot ábrázoltunk (fehér). A kék színű hiperbola a z = 0.5 síkkal való metszete, a piros színű hiperbola pedig a z = -0.5 sikkal való metszete.

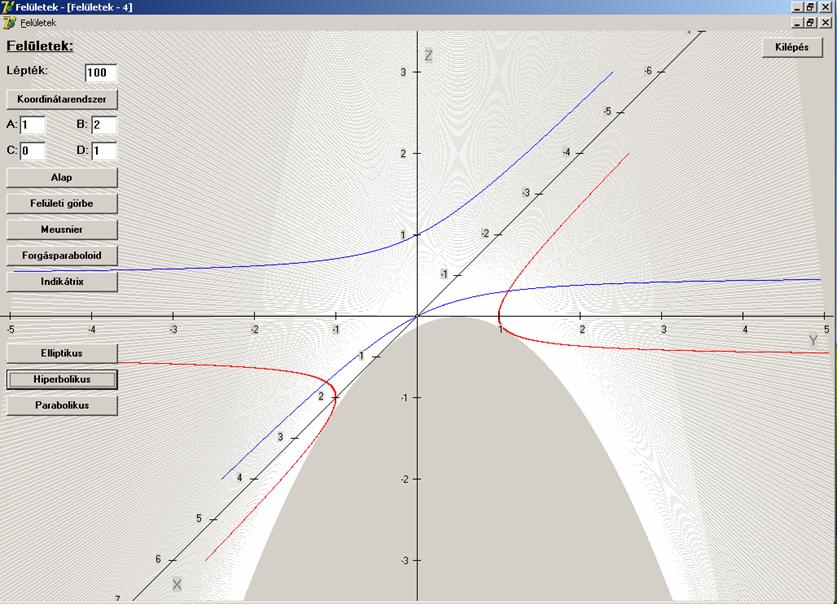
A harmadikon egy parabolikus henger (fehér) látható. A két kék egyenes a z = 0.5 síkkal való metszete.

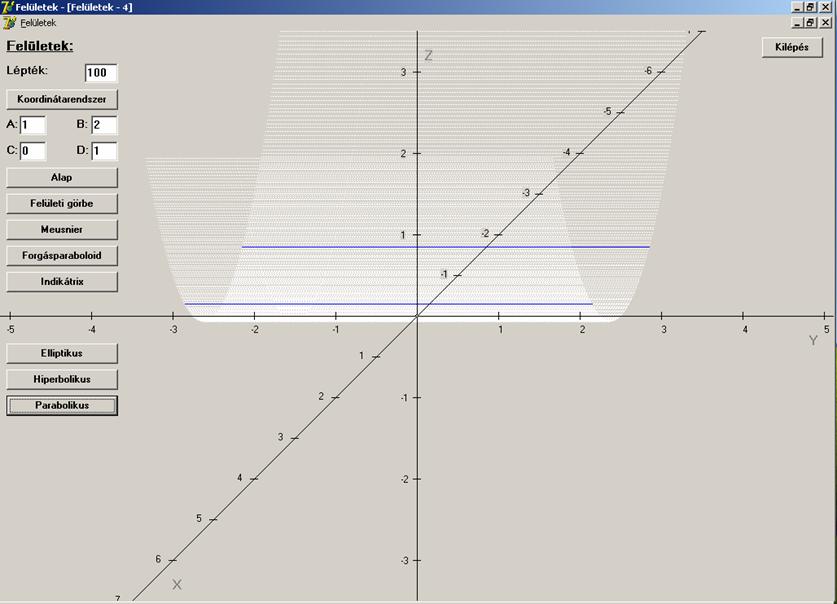
Megjegyezzük, hogy ha a felület egy adott pontja érintő síkjában minden irányban felmérjük az irányhoz tartozó normárgörbület reciprokának a négyzetgyökét, akkor a Dupin-féle indikátrix pontjait kapjuk.

Igazak továbbá a következők:

- a felület elliptikus pontjainak elég kis környezetében a felület minden pontja a pontbeli érintősík egyik oldalán helyezkedik el.

- a felület hiperbolikus pontjainak tetszőleges kicsiny környezetében vannak olyan pontok, amelyekből az egyik az érintősík egyik, a másik az érintősík másik oldalán helyezkedik el, azaz az érintősík a felületet metszi is.

- a felület parabolikus pontjainak elég kis környezetében lévő pontok az érintő sík egyik oldalán vagy az érintősíkon vannak.

Egy hiperbolikus vagy parabolikus pontokon áthaladó olyan felületi görbét, melynek minden érintője az ottani Dupin-féle indikátrix valamelyik asszimptótája, illetve parabolikus pontokban az egyenes-pár irányába mutat, asszimptota vonalnak nevezzük. Asszimptóta irányokhoz tartozó normálgörbület értéke nulla. Képletben:

Elliptikus pontokon nem megy át asszimptota vonal. Parabolikus pontokon egy asszimptóta vonal, hiperbolikus pontokon két asszimptota vonal halad át. Ha egy asszimptota vonal görbülete nem tűnik el, akkor ebben az esetben a felületi görbe főnormálisa és a felület normál egységvektora egymásra merőleges. Ezt az esetet az utóbbi vizsgálatainkból kizártuk, vagyis azt, amikor a görbe simulósíkja és a felület érintősíkja egybeesik.

Azokat a felületi görbéket, amelynek érintője mindig az illető pontban érvényes valamelyik főirányba, azaz a Dupin-féle indikátrix tengelyirányába mutat, görbületi vonalaknak nevezzük. A felület minden pontján két görbületi vonal halad át, melyek egymásra merőlegesek.

Példaként osztályozzuk a fentiek szerint egy tórusz felületi pontjait. A tórusz paraméteres egyenletrendszere (ahol R > r):

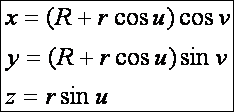
A tórusz második alapmennyiségei:

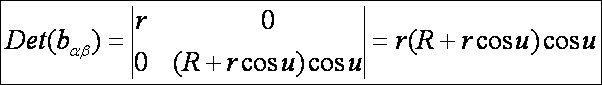
Parabolikus pontokra:

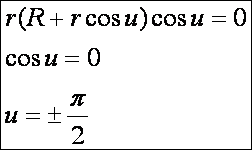
Elliptikus pontokra:

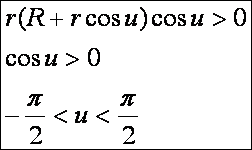
Hiperbolikus pontokra:

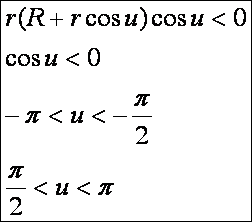
Mindezt egy rajzon is megnézhetjük. A z = B és z = -B síkok a tóruszt egy-egy körben érintik. A rajzon ezek a körök feketével láthatók. A tórusz felületi pontjai közül ezek a parabolikus pontok. A tórusz külső része, a fehérrel jelölt pontok az elliptikus pontok, a tórusz belső része, a sárgával jelöltek a felület hiperbolikus pontjai. Látható, hogy a parabolikus és a hiperbolikus pontokat elliptikus pontok választják el egymástól.

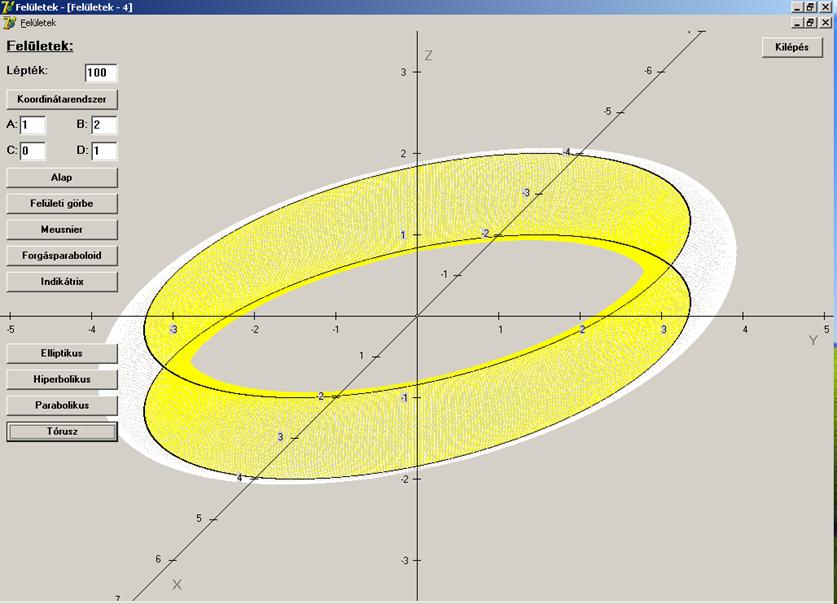
Befejezésként minősítsük a következő felület pontjait:

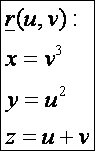
Meghatározzuk a felület második alapmennyiségeit. Az első deriváltak:

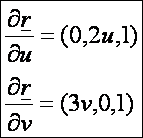
A normálvektor:

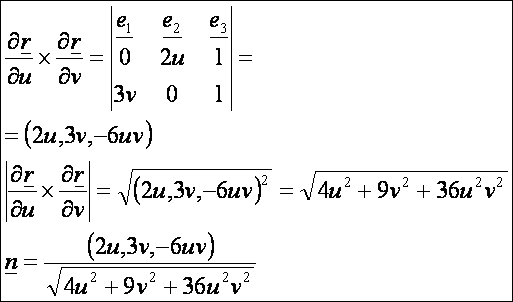
A második deriváltak:

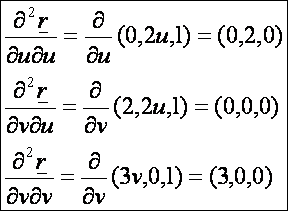
A második alapmennyiségek:

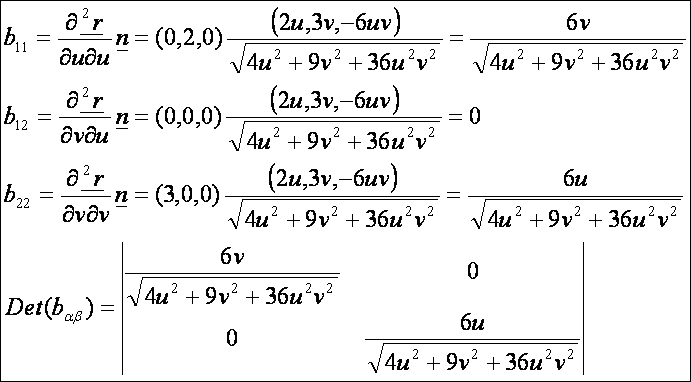
A parabolikus pontokra:

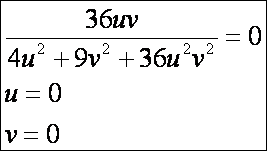
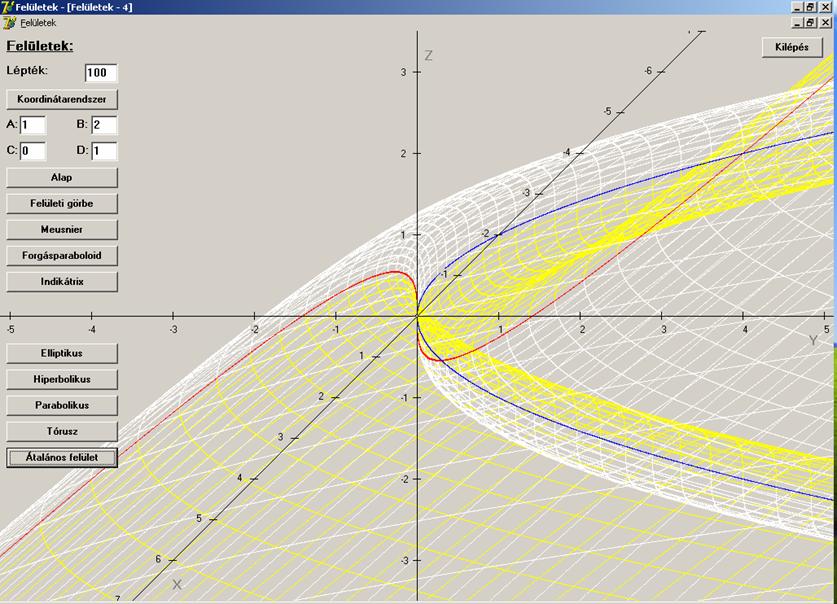
A rajzon piros az u = 0 paramétervonal, kék a v = 0 paramétervonal, amelyeken a felület parabolikus pontjai találhatók. Ahol uv > 0, ott a felületnek elliptikus pontjai vannak és fehérek a paramétervonalak, ahol uv < 0 ott a felületnek hiperbolikus pontjai vannak és sárgák a paramétervonalak.

Következő lap: http://gorbem.hu/MT/DiffGeom16.htm