Differenciálgeometria (14)

Felületek második alapmennyiségei

Ha egy felületet a pontja környezetében Taylor-sorba fejtünk (egy felülettel közelítjük), úgy hogy a másodfokúnál magasabb tagokat elhanyagoljuk, akkor egy olyan másodrendű felületet kapunk, amely az eredetit másodrendben közelíti, és amelynek egyenlete:

A következő rajzon a fehér a vizsgált felület, a piros a Taylor-sorral előállított másodrendű felület, sárga az érintő sík. Az r vektor a felületre, az vektor a másodrendű felületre, az r₀ a P₀ érintési pontba mutató vektor. Az e₁ és e₂ vektorok a paramétervonal-érintők, amelyek felfeszítik az érintő síkot, az n vektor az érintősíkra merőleges és normálvektora az felületnek és a másodrendű felületnek is. Ennek a három felületnek egyetlen közös pontja van a P₀.

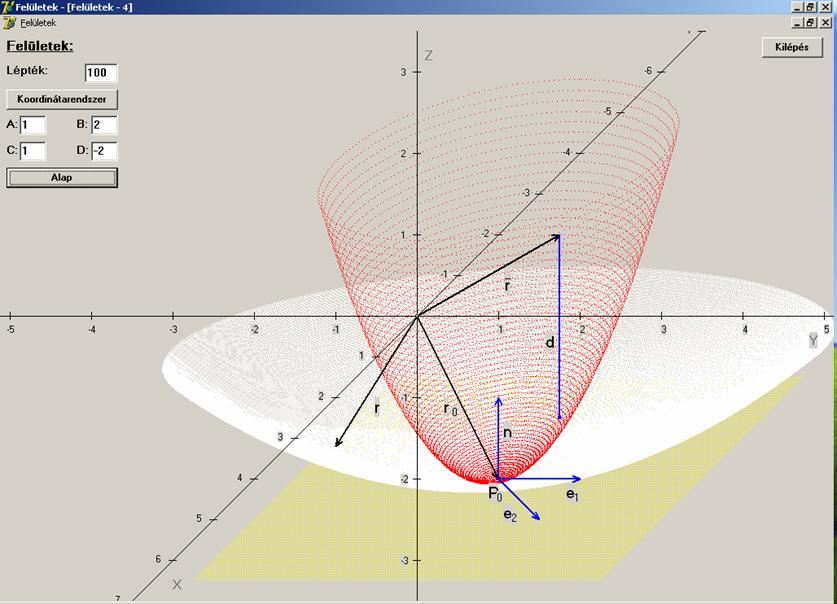
A d a másodrendű felület egy pontjának távolsága az érintő síktól. Ezt a d távolságot a következőképpen kapjuk:

Az ebben a képletben szereplő belső szorzatokat a felület második alapmennyiségeinek nevezzük és így jelöljük:

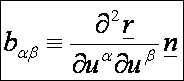
Az alapmennyiségek száma összesen négy. Ezek közül viszont a kétszer folytonosan differenciálható felületek esetén csak három lesz különböző, hiszen ebben az esetben a vegyes parciális deriválás sorrendje felcserélhető. Ezt a három mennyiséget Gauss L, M és N -el jelölte, azaz:

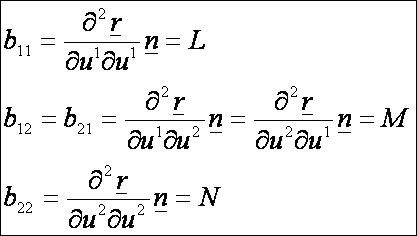
A második alapmennyiségekkel képzett

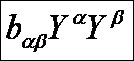
kvadratikus formát a felületek második alapformájának nevezzük.

Ha a P₀ pontban felveszünk egy olyan koordinátarendszert, melynek a paramétervonal-érintők és a pontbeli normálvektor az egységvektorai, akkor a fentebbi közelítő felület egyenlete:

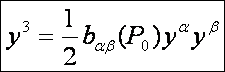
ahol yⁱ a lokális koordinátarendszerre vonatkozó koordinátákat jelöli. Jól látható, hogy ez egy paraboloidnak az egyenlete. Ezt a közelítő felületet oszkuláló paraboloidnak nevezzük.

Itt jegyezném meg, hogy a felületek első alapmennyiségeiben a felületnek az első deriváltjai szerepelnek, itt viszont a második deriváltak. Az első alapmennyiségek az ívhossz, a szög és felszínmérésben játszottak szerepet, azaz a felület metrikáját határozták meg. Nem mondtak semmit a felületnek a háromdimenziós Euklideszi térbe való beágyazásáról, a felület alakjáról. Mindezt jól mutatja az a példa, amikor egy síklapot hengerré vagy kúppá hajlítunk, akkor a felületi metrika nem változik (itt az egymásnak megfelelő pontokban az első alapmennyiségek azonosak), a térbeli forma, alak viszont igen. Ennek a formának a leírására lesznek alkalmasak a felület második alapmennyiségei.

Néhány felület második alapformája

A gömb

A gömb szokásos paraméteres előállítása:

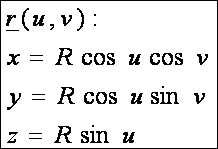
Az első deriváltak:

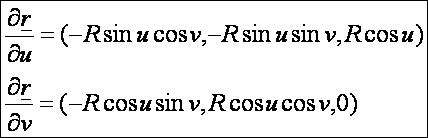
A normálvektor:

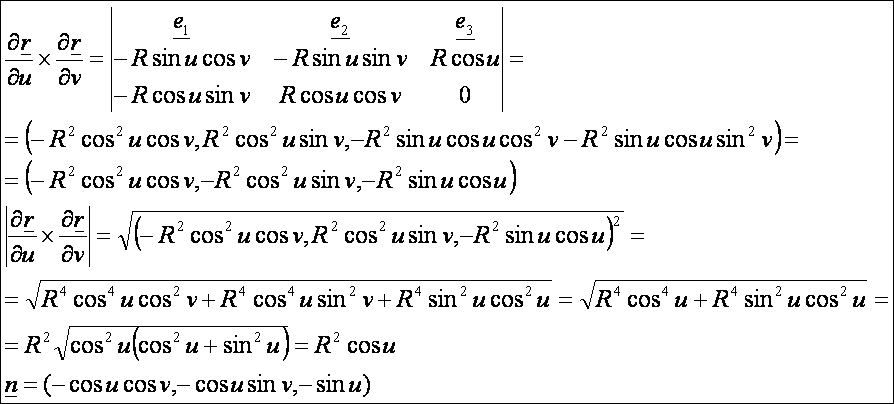
A második deriváltak:

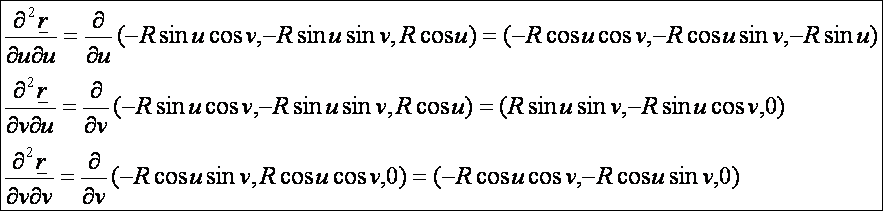
A második alapmennyiségek:

A gömb második alapformája:

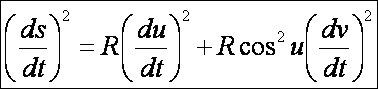
Emlékeztetőül az első alapforma:

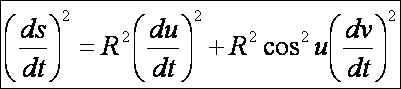
Az első alapforma a másodiknak az R –szerese.

A körhenger

A körhenger paraméteres előállítása:

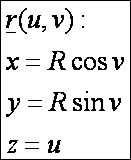
Az első deriváltak:

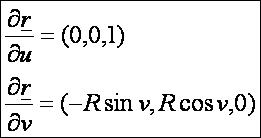
A normálvektor:

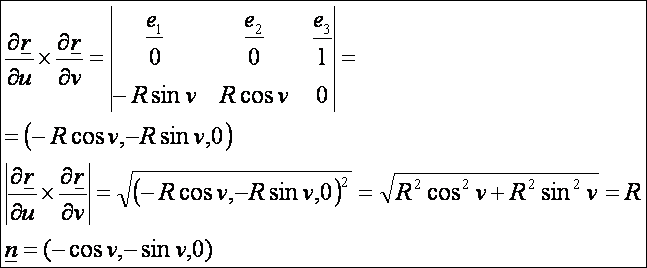
A második deriváltak:

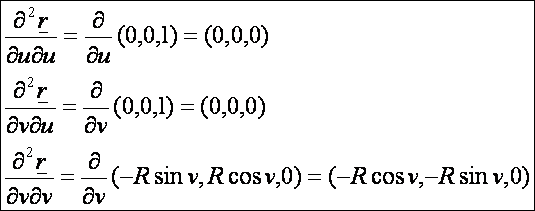
A második alapmennyiségek:

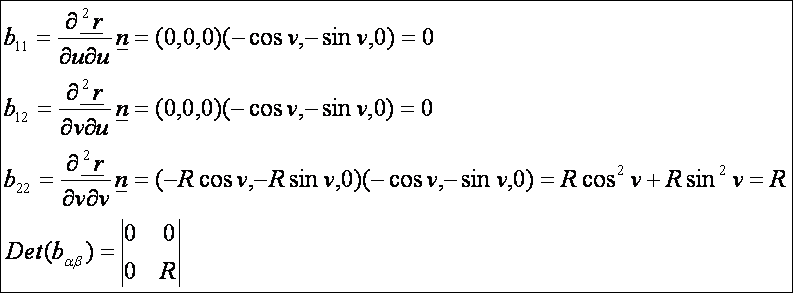
A henger második alapformája:

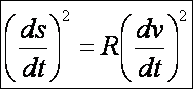
A kúp

A kúp paraméteres előállítása:

Az első deriváltak:

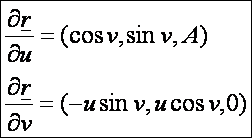
A normálvektor:

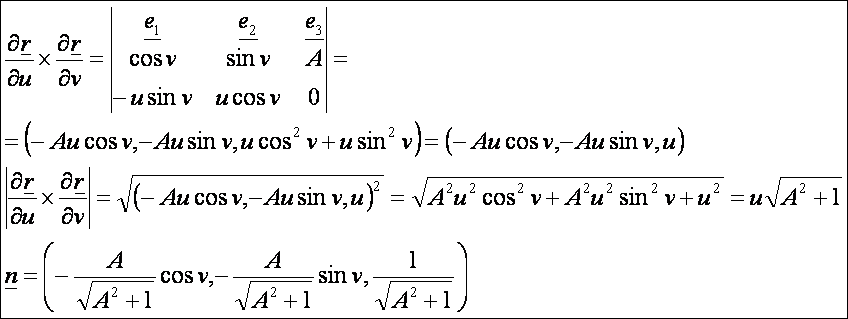
A második deriváltak:

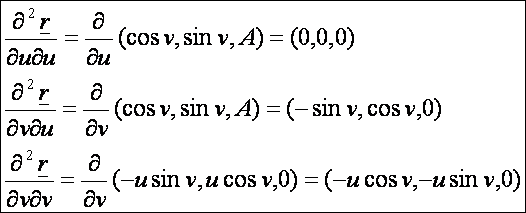
A második alapmennyiségek:

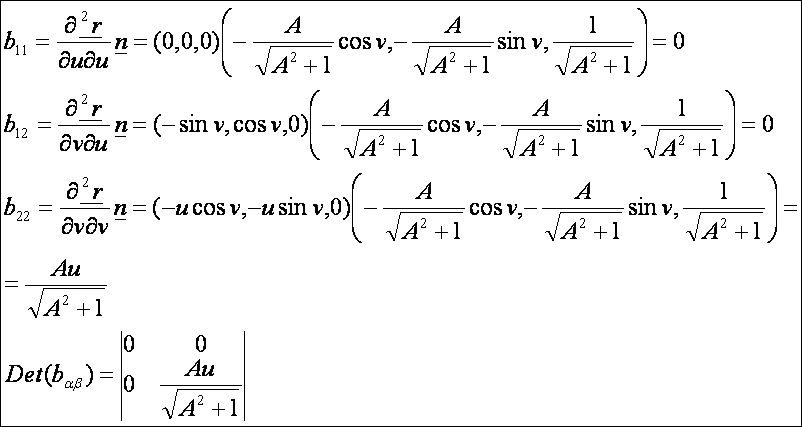
A kúp második alapformája:

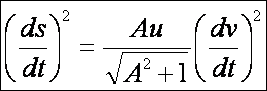
Az egyenes csavarfelület

Az egyenes csavarfelület paraméteres előállítása:

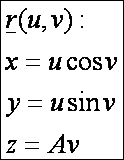
Az első deriváltak:

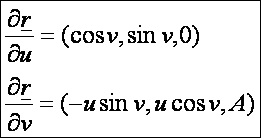
A normálvektor:

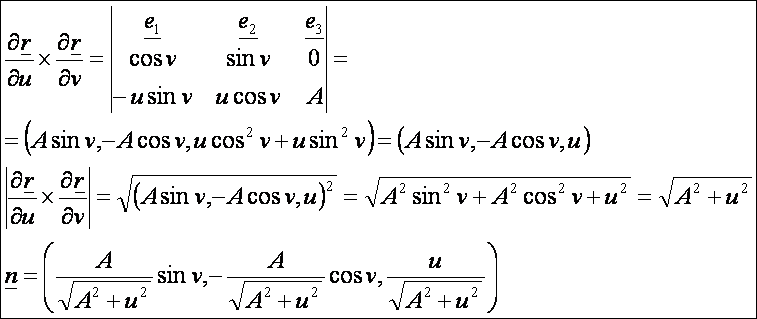
A második deriváltak:

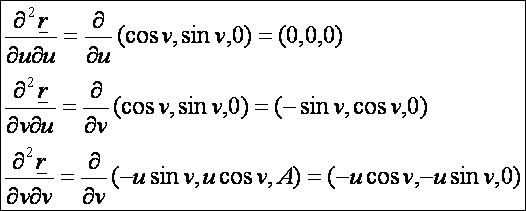
A második alapmennyiségek:

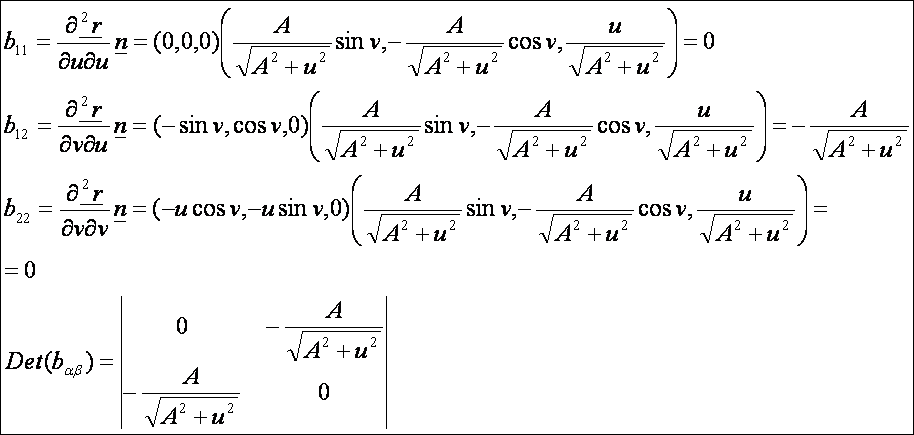
Az egyenes csavarfelület második alapformája:

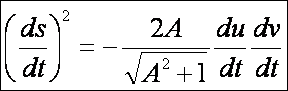
A hiperbolikus paraboloid

A hiperbolikus paraboloid paraméteres előállítása:

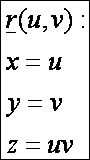
Az első deriváltak:

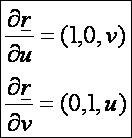
A normálvektor:

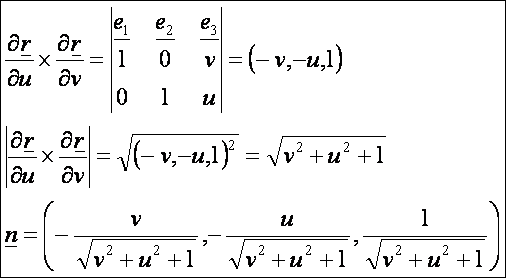
A második deriváltak:

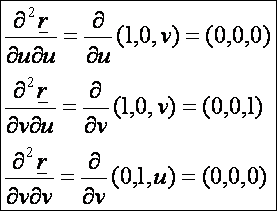
A második alapmennyiségek:

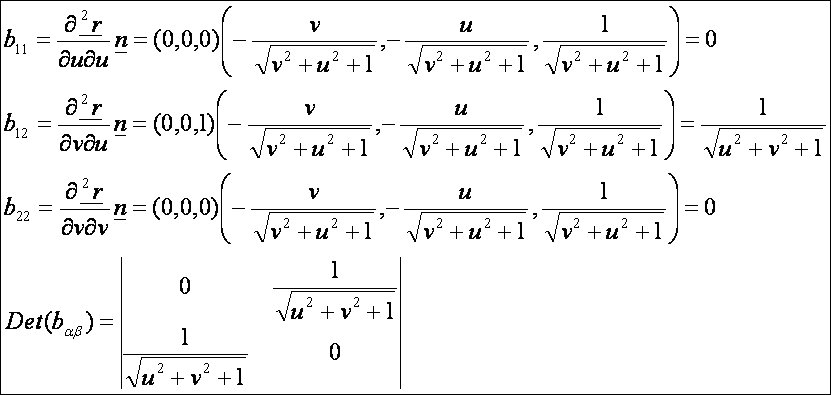
A hiperbolikus paraboloid második alapformája:

A forgásparaboloid

Az forgásparaboloid paraméteres előállítása:

Az első deriváltak:

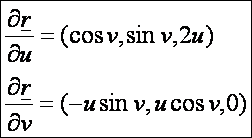
A normálvektor:

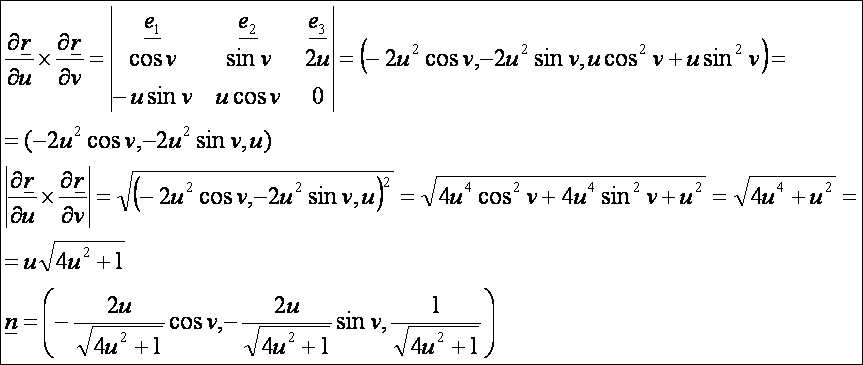
A második deriváltak:

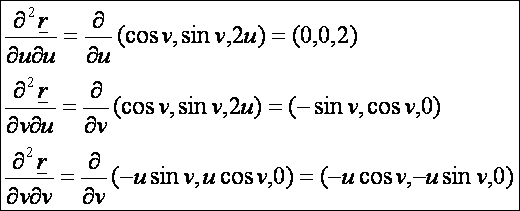
A második alapmennyiségek:

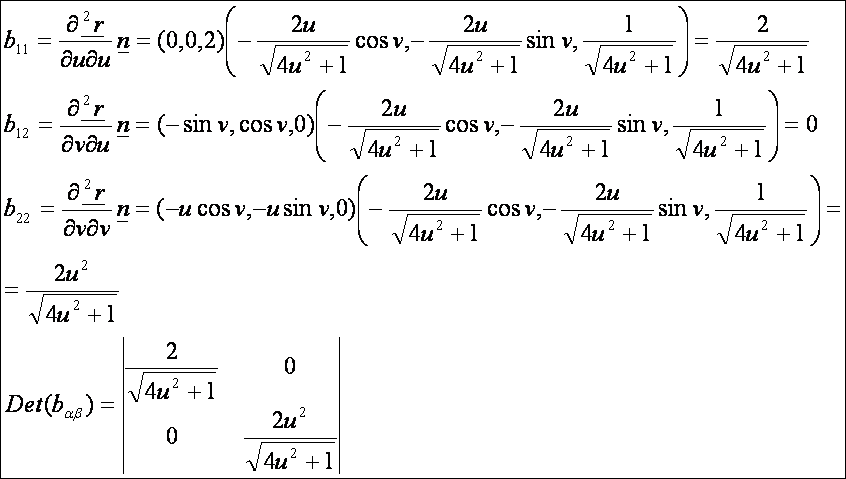
A forgásparaboloid második alapformája:

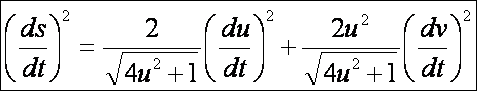
A katenoid

A katenoid a koszinusz hiperbolikusz függvény forgásfelülete, amelynek paraméteres előállítása:

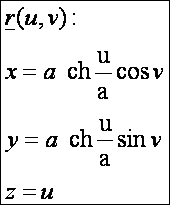
Az első deriváltak:

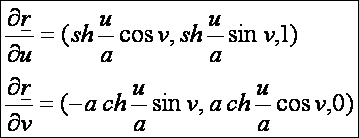
A normálvektor:

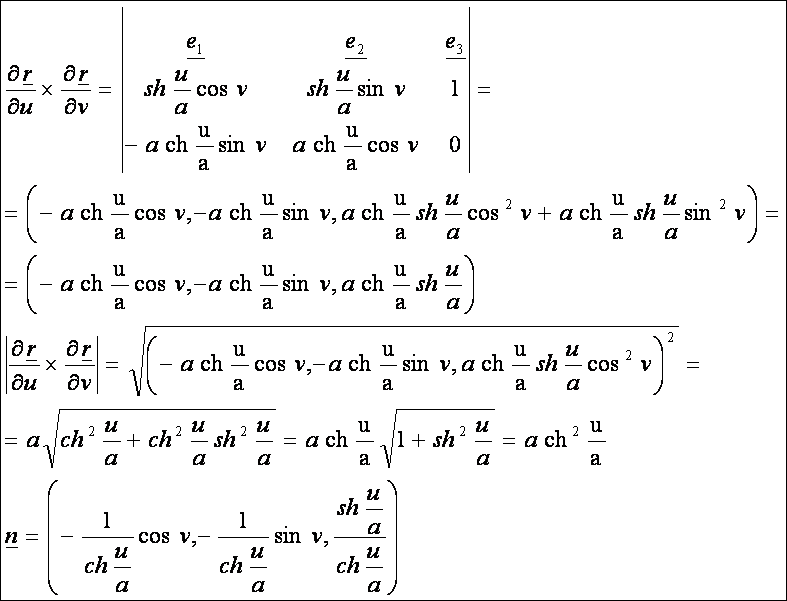
A második deriváltak:

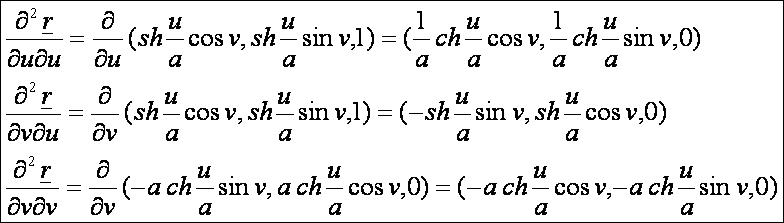
A második alapmennyiségek:

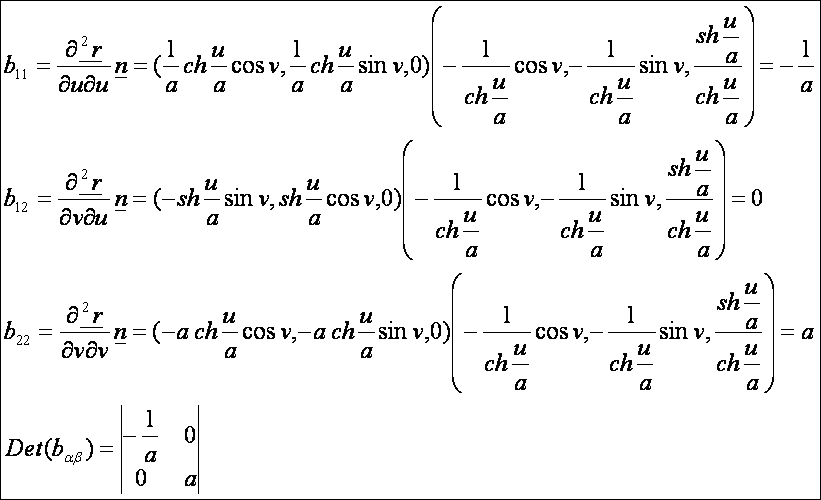
A katenoid második alapformája:

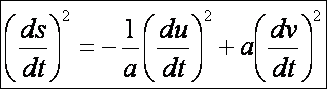
A sík

A sík paraméteres előállítása:

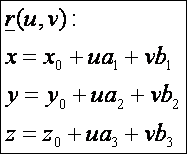
Az első deriváltak:

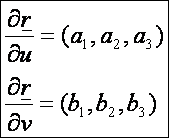
A normálvektor:

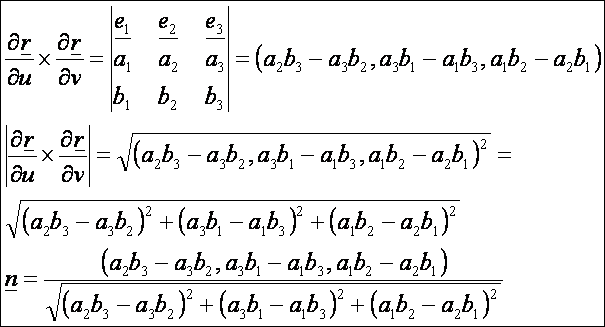
A második deriváltak:

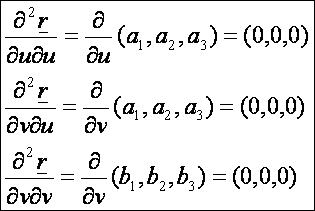
A második alapmennyiségek:

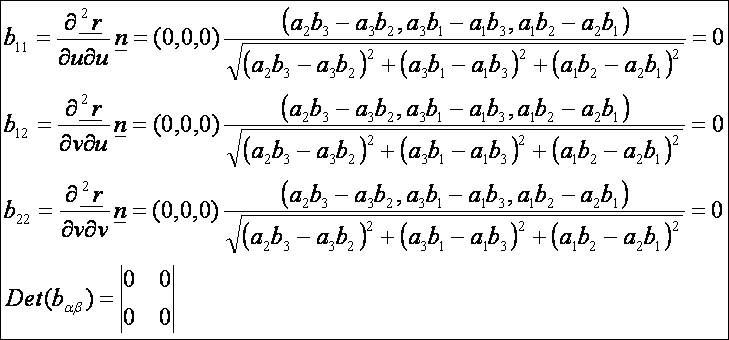
A sík második alapformája:

A forgásellipszoid

A forgásellipszoid paraméteres előállítása:

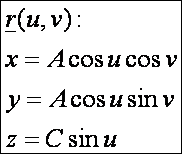
Az első deriváltak:

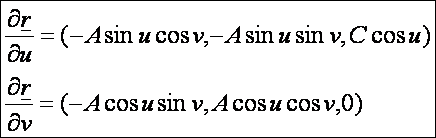
A normálvektor:

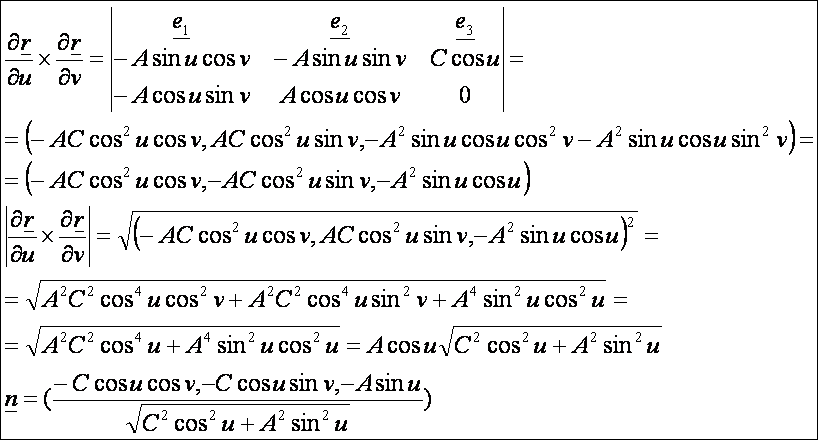
A második deriváltak:

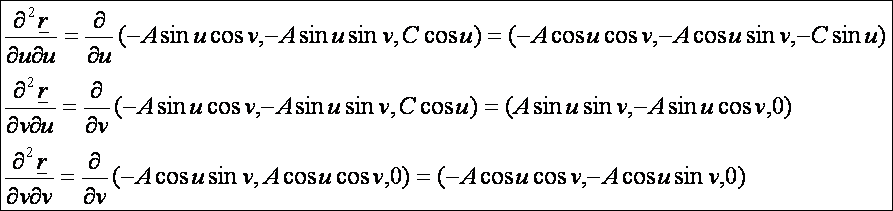
A második alapmennyiségek:

A forgásellipszoid második alapformája:

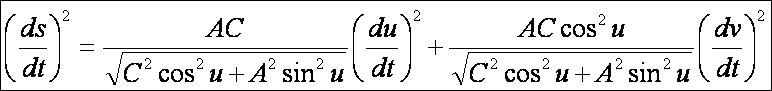
Az egyköpenyű forgáshiperboloid

Az egyköpenyű forgáshiperboloid paraméteres előállítása:

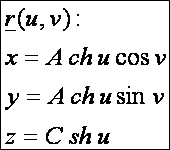
Az első deriváltak:

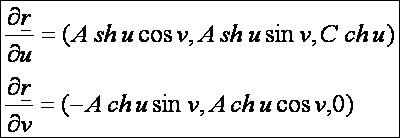
A normálvektor:

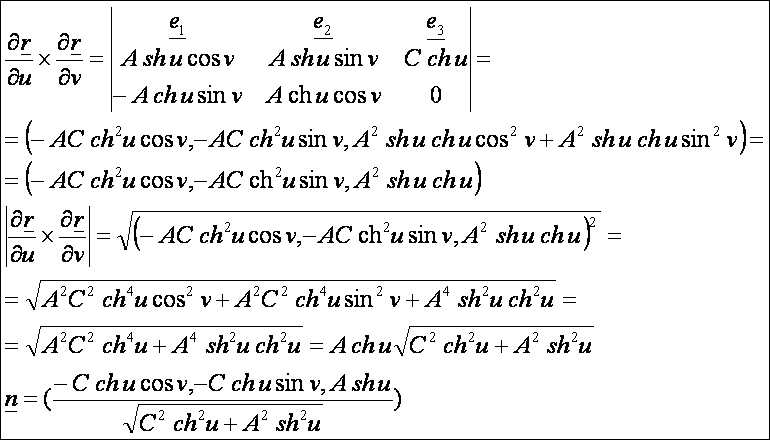
A második deriváltak:

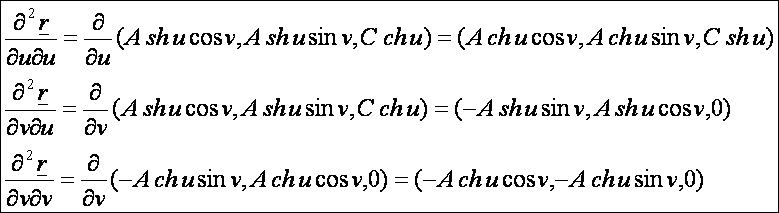
A második alapmennyiségek:

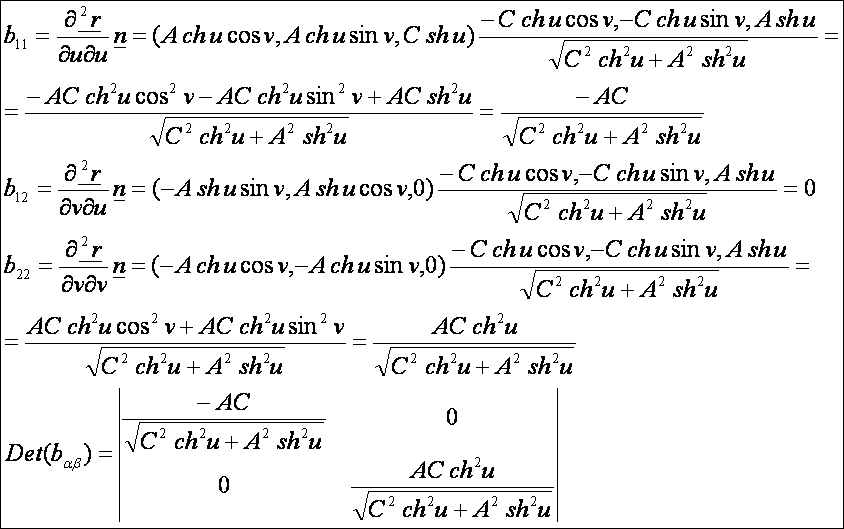
Az egyköpenyű forgáshiperboloid második alapformája:

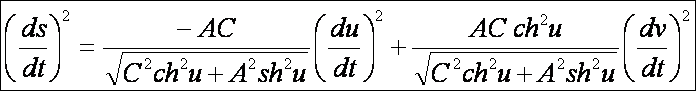
A kétköpenyű forgáshiperboloid

A kétköpenyű forgáshiperboloid paraméteres előállítása:

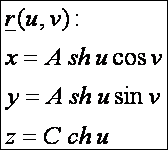
Az első deriváltak:

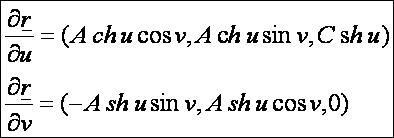
A normálvektor:

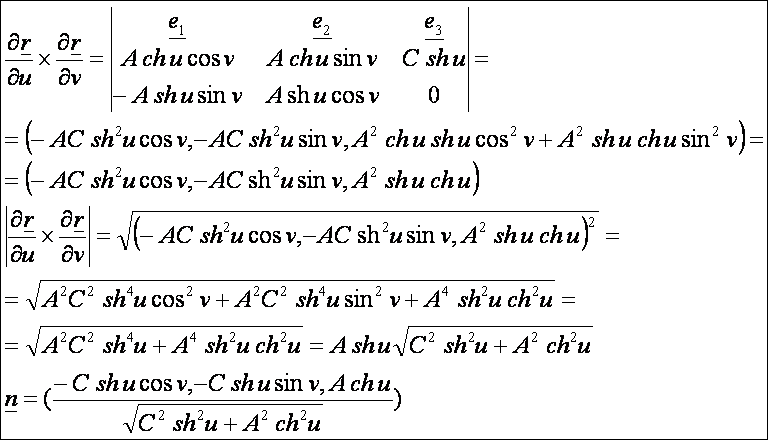
A második deriváltak:

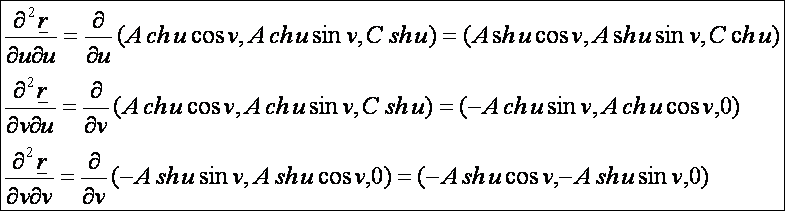
A második alapmennyiségek:

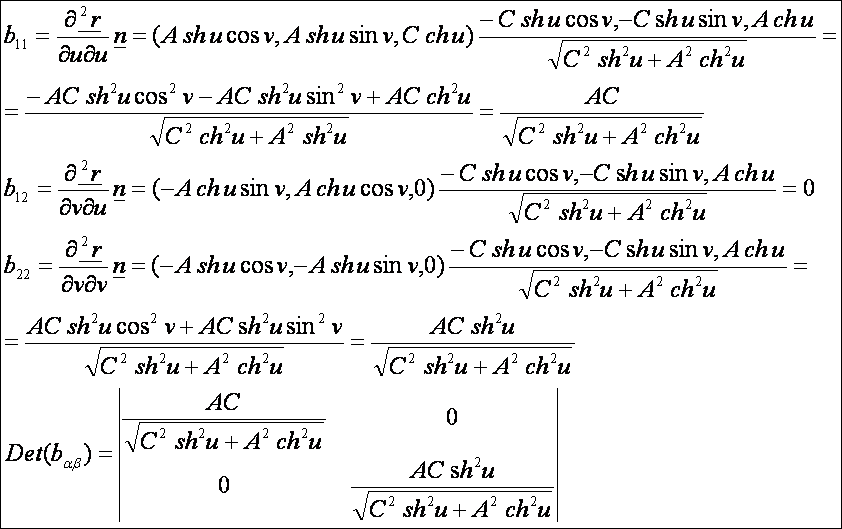
A kétköpenyű forgáshiperboloid második alapformája:

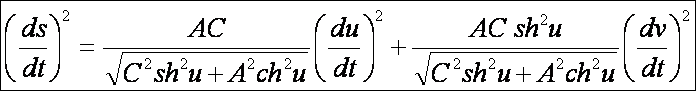
A tórusz

A tórusz paraméteres előállítása:

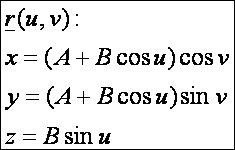
Az első deriváltak:

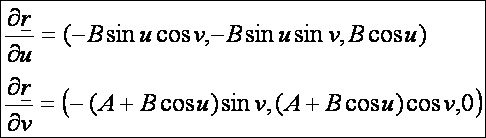
A normálvektor:

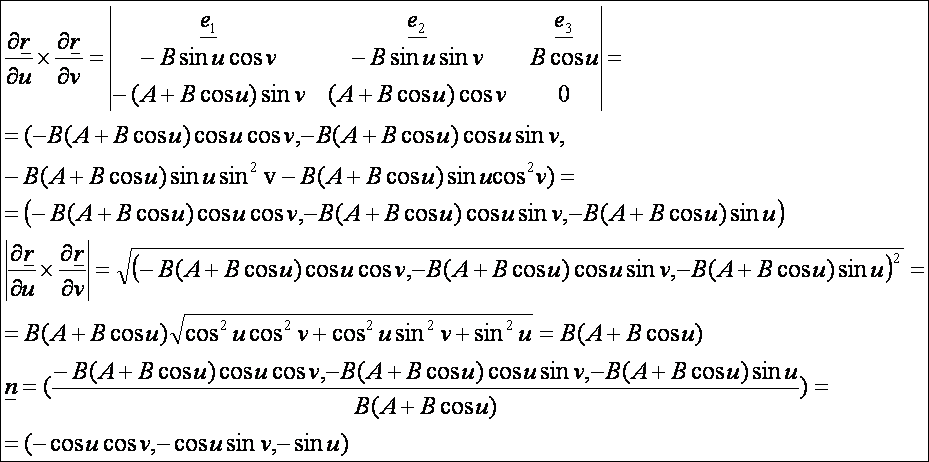
A második deriváltak:

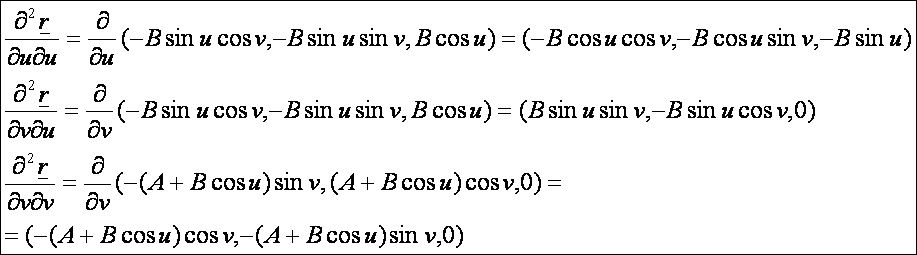
A második alapmennyiségek:

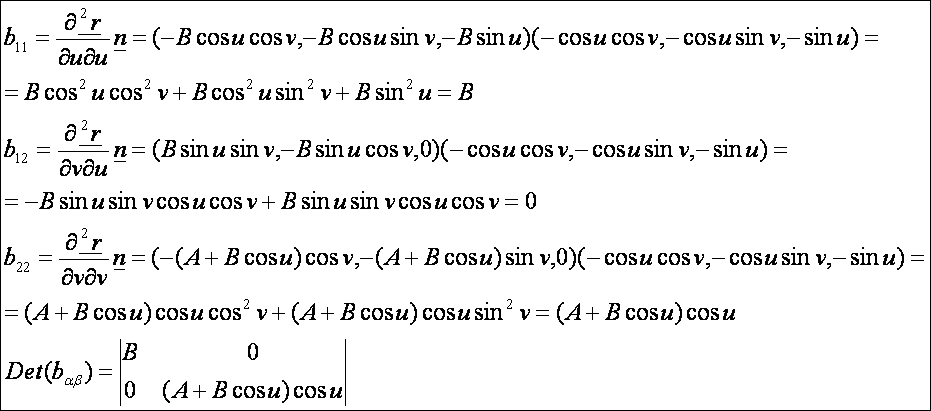
A tórusz második alapformája:

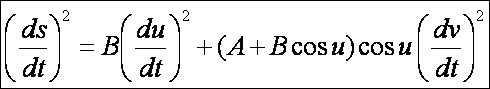
Következő lap: http://gorbem.hu/MT/DiffGeom15.htm