Abszolút érték (1)

Fogalma: egy valós szám abszolút értékén értjük magát a számot, ha a szám nem negatív és negatívját, ha a szám negatív (vagyis mindenképpen egy nem negatív számot). Az abszolút érték a számegyenesen kifejezi a számnak a 0 -tól mért távolságát (a számegyeneses érvényes egységben mérve, ami a 0 és az 1 távolsága). Nyilván csak egyetlen számnak, a 0 -nak az abszolút értéke nulla.

Az abszolút érték segítségével függvényeket is megadhatunk. A legegyszerűbb ilyen függvény az . Legtöbbször – naiv egyszerűséggel – ezt szokták abszolút-értékes függvénynek nevezni. Ezt azért nevezném problémásnak, mert minek nevezzük akkor az olyan egyéb (számtalan sokféle) függvényt, aminek képletében az abszolút-érték jele szerepel.

Az illendőség kedvéért azért felsorolnám az függvény legfontosabb tulajdonságait. A függvény az értelmezési tartományának minden pontjában folytonos. Értelmezési tartománya a valós számok halmaza, értékkészlete a nem negatív valós számok halmaza. A intervallumban szigorúan monoton csökken (képe félegyenes, meredeksége -1). A intervallumban szigorúan monoton nő (képe félegyenes, meredeksége 1). Alakja V betűt formáz. A (0, 0) pontban töréspontja van. Ebben a töréspontban a függvénynek abszolút minimuma van – aminek az értéke 0. Ennek a pontnak a kivételével minden pontban differenciálható, deriváltja az előjelfüggvény (Az előjelfüggvénynek a jele: SGN(X), mely negatív számhoz -1 -et, pozitív számhoz +1 -et, nullához 0-t rendel – ami itt most kimarad a deriváltból). A függvény képe:

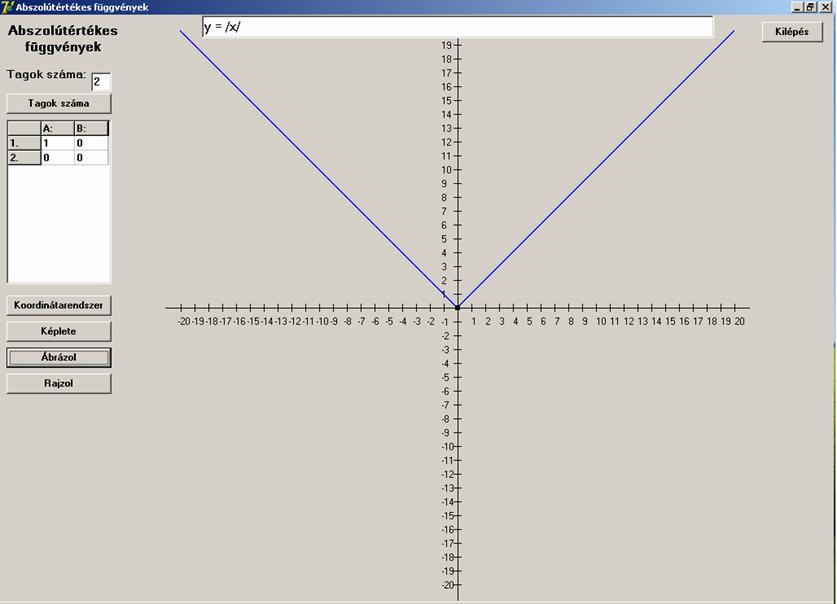
Explicit alakú abszolút-értékes függvények.

A fentieknél ez a jegyzet egy kicsit többre vállalkozik. Legalább arra, hogy néhány egyszerűbb esetre nézve egy átfogó képet alkosson az abszolút-érékes függvények tulajdonságairól. Elsőként a következő függvénycsoportról lesz szó: egyváltozós, elsőrendű, lineáris, rendezett abszolút-értékes explicit függvényekről, amely ezen belül lehet homogén, vagy vegyes.

Magyarázat:

Egyváltozós: a független változók száma egy.

Elsőrendű: a képletben nincs egymásba ágyazott abszolútérték-jel.

Lineáris: a változók hatványkitevője 1.

Rendezett: a képletben a tagok a benne szereplő konstansok csökkenő rendjében szerepelnek (csak a könnyebb olvashatóság és az ábrázolás miatt). Minden abszolút értéken belüli független változónak az együtthatója 1.

Explicit: a függő változó ki van fejezve a függvény egyenletében (az egyik oldalon csak ő szerepel és máshol nem található az egyenletben).

Homogenitás: vegyes, ha van benne olyan független változót tartalmazó tag, amely nincs abszolútérték-jelbe zárva, egyébként homogén.

Példa egy ilyen függvényre:

Ez a függvény nem homogén, hanem vegyes, mert az abszolút-értékes tagok mellett van egy olyan tag is, amelynek független változója nincs abszolút-értékbe zárva (-x). Minden, a leírásnak megfelelő explicit függvény képlete ilyen alakra hozható (az abszolút-értékből való kiemeléssel, az abszolút értéken belüli előjelváltással (), esetleg összevonással és rendezéssel (tagok cseréjével).

Természetesen a függvények ábrázolására (mert egyelőre ez lesz a fő cél) írtam egy programot. Nézzük is meg, hogyan fest az előző függvény:

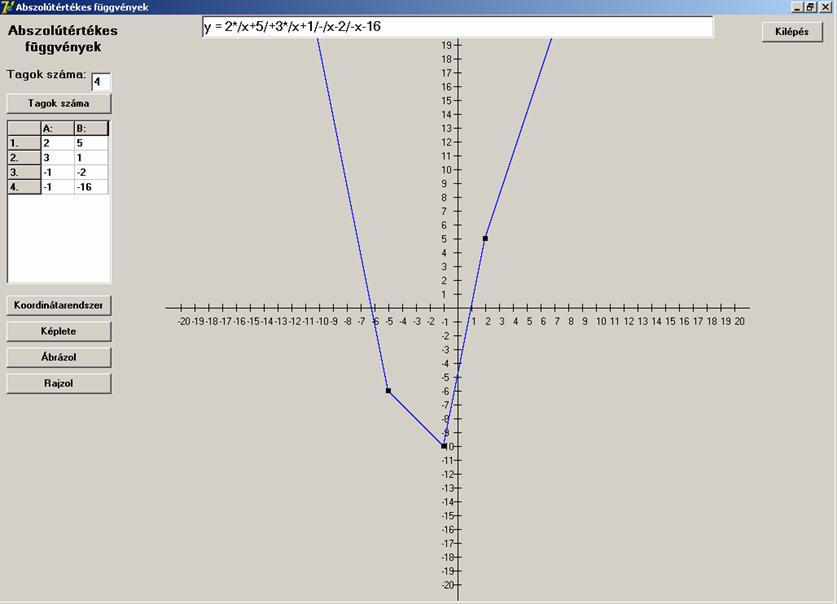
A töréspontokat fekete négyzetek jelölik. A rendezettségnek itt van jelentősége. A töréspontok x koordinátája rendre a tagok belsejében lévő konstansok negatívja: -5, -1 és 2. A törött vonal meredekségei pedig az együtthatókból adódnak:

Töréspontok		-5		-1		2
Együtthatók	2		3		-1		-1
Tartományok	x<-5		-5<x<-1		-1<x<2		x>2
Homogén rész meredeksége	-2-3+1 = -4		2-3+1 = 0		2+3+1 = 6		2+3-1 = 4
Inhomogén rész meredeksége	-1		-1		-1		-1
Végső meredekség	-4-1 = -5		0-1 = -1		6-1 = 5		4-1 = 3

Tehát a meredekségek: -5, -1, 5 és 3. Amellett, hogy a fenti táblázat minden éréke helyes, egy kicsit számolós az ellenőrzése. Annak érdekében, hogy átláthatóbb legyen a meredekségek kiszámításának módja, általános alakban is megadjuk a számolás menetét. Ehhez a függvényben azonosítókat vezetünk be a meredekségekre és a konstansokra is. Íme a képlet:

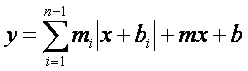
Azért m -et választottunk együtthatóknak, mert ezek a függvény meredekségeit fogják adni. Egyébként az egyenes tengelymetszetes alakja is ilyen jeleket használ: y = mx + b. Az összegzést azért csak n-1-ig hajtjuk végre, mert így illeszkedik a rajzoláshoz használt programhoz, ahol az inhomogén rész az n. tag. Jelölje M_i az egyes szakaszok meredekségét. Ezek a képletben szereplő m_i -kel így fejezhető ki (n= 4 esetén, három töréspont négy szakasszal):

M₁ = -m₁-m₂-m₃+m

M₂ = m₁-m₂-m₃+m

M₃ = m₁+m₂-m₃+m

M₄ = m₁+m₂+m₃+m

A képzési szabályból ez adódik az egymást követő meredekségekre:

, , és

Megjegyezném, hogy ha az M₁ és M₄ egymásnak negatívja, akkor az m éréke 0, azaz a függvény homogén. Megfordítva, ha a függvény homogén, akkor az első és utolsó meredekség egymás additív ellentettje. Ezek után a következő lépésekkel lehet a legkönnyebben ábrázolni a tárgyalt típusú abszolútértékes-függvényeket:

1. Hozzuk rendezett alakra (együtthatók, konstansok csökkenő sorrendben).

2. Számítsuk ki –b₁-nél a helyettesítési értéket, legyen ez h₁. Az első töréspont balról jobbra haladva (-b₁, h₁), amit felvehetünk a koordinátarendszerbe.

3. Számítsuk ki a M_i-ket a fentebbi szabály szerint.

4. Az M_i-k, a balszélső pont és a töréspontok x koordinátája segítségével a szakaszok – azaz a függvény grafikonja – már megrajzolható.

Ezek után rajzoltassunk még néhány érdekes alakú függvényt a programmal – ha már úgyis könnyen megy neki. Először néhány homogén esetet lássunk. Legyen alakja árokhoz hasonló:

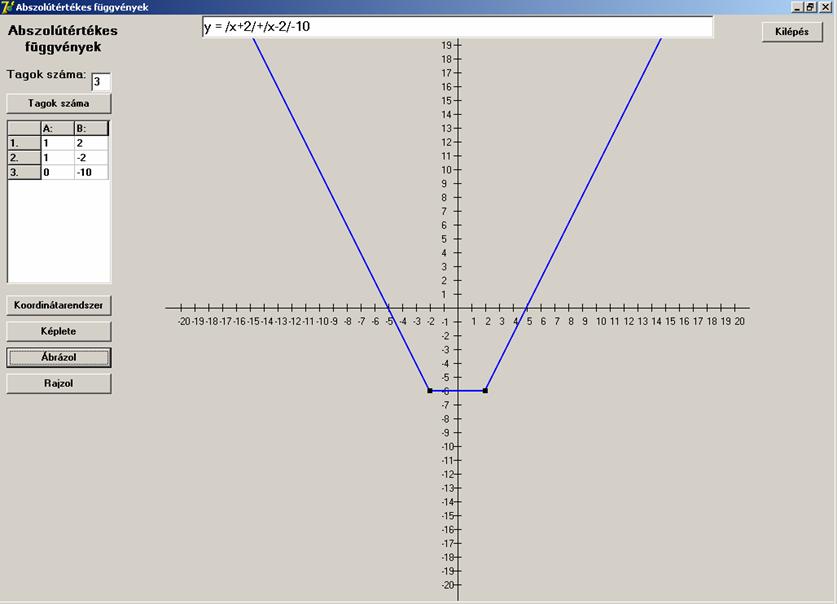
Legyen W alakú:

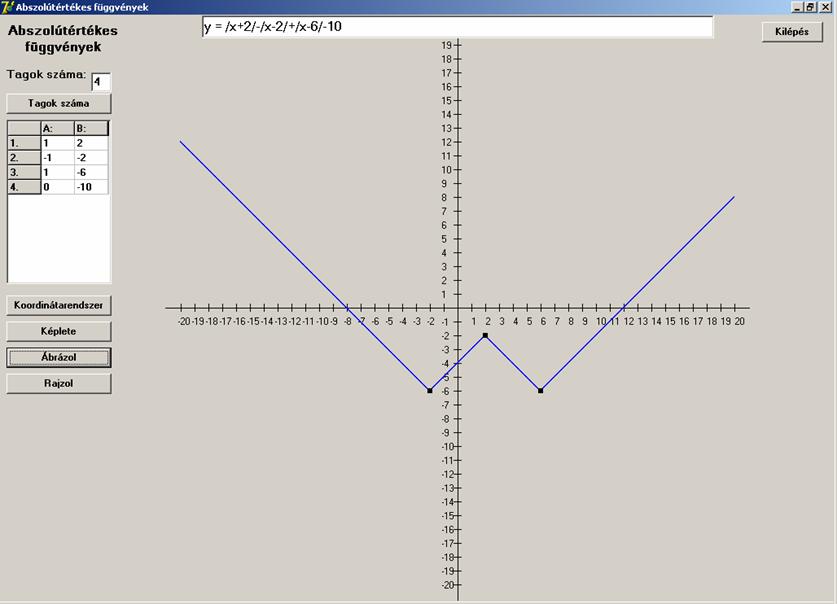
Tartalmazzon sok töréspontot, legyen fűrészfog alakú:

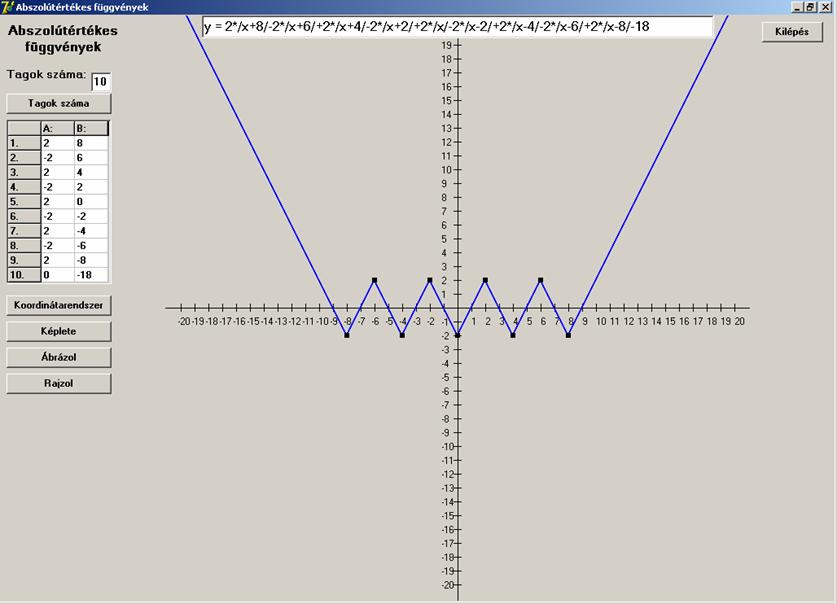
Legyen lépcső alakú:

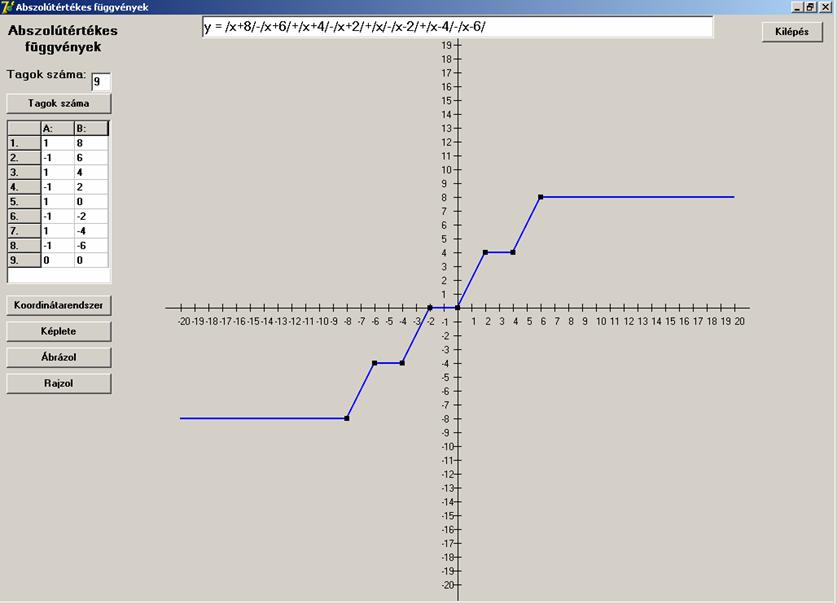
Végül legyen kettős domb alakú (trapézjel egy részlete):

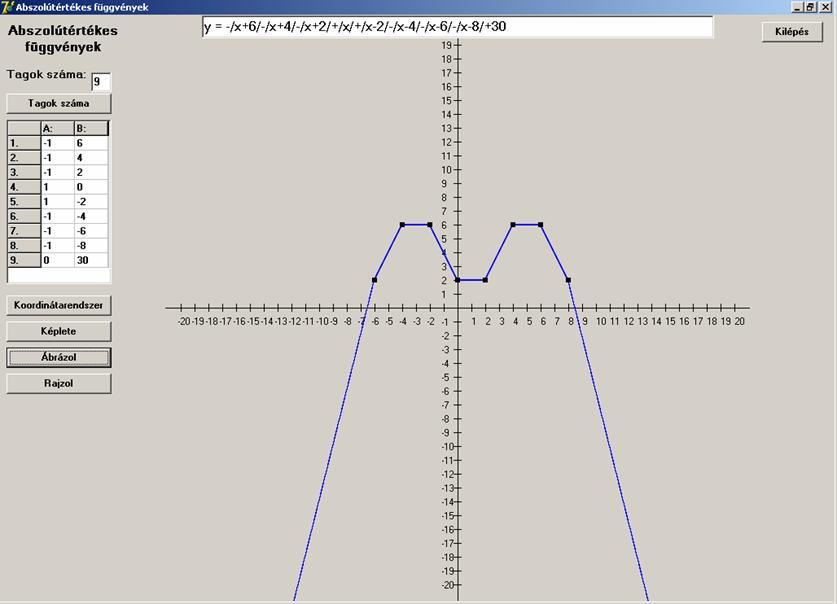
Ezek után következzen néhány inhomogén eset. Először legyen olyan, mint egy meredek hegyoldal a síkság mellett:

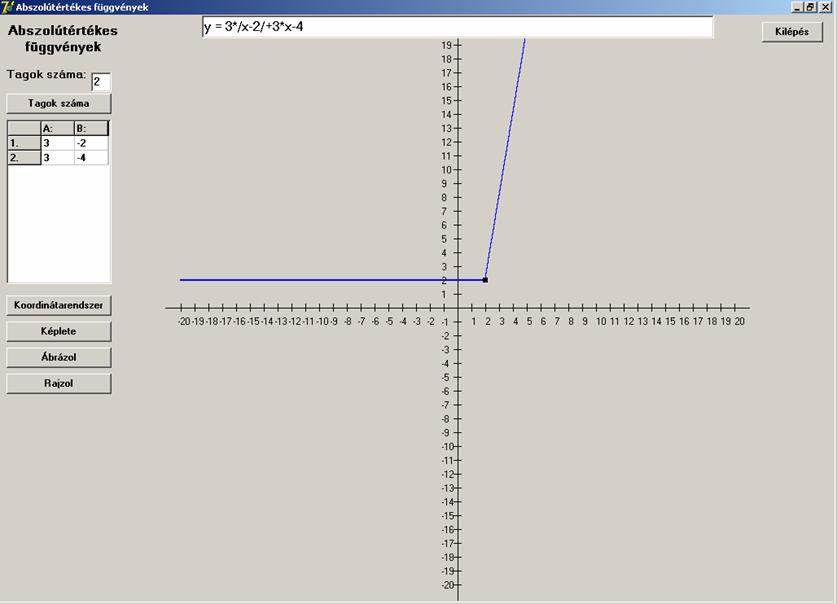
Következő nézzen úgy ki, mint egy villám:

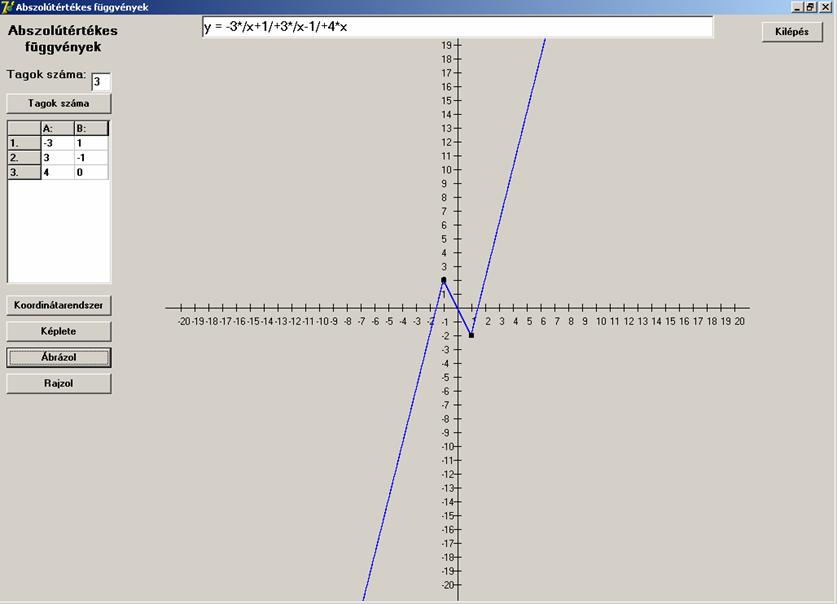
Végül pedig egy látványos:

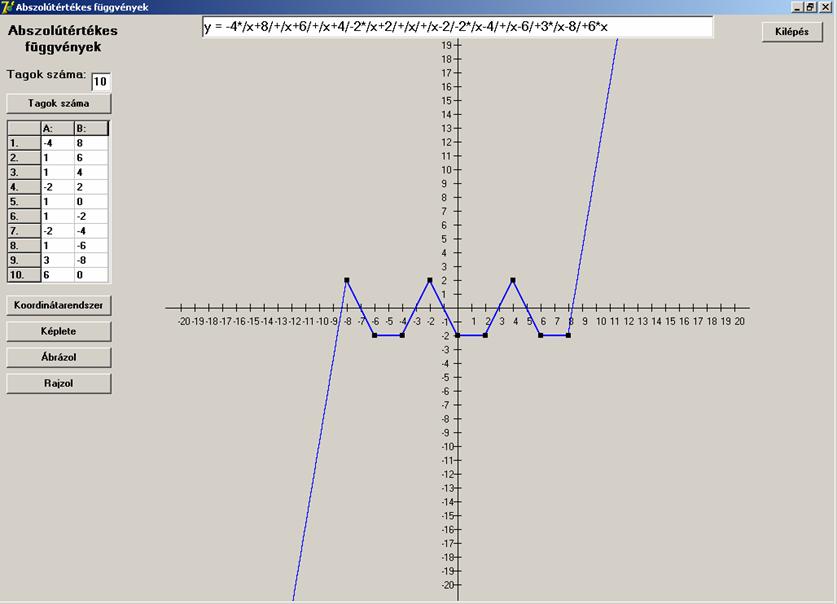
A feladat meg is fordítható a következő értelemben. Rajzoljunk egy tetszőleges összefüggő törött vonalat a koordinátarendszerbe. (Természetesen olyat, amely függvényt ad meg, azaz bármely, y tengellyel párhuzamos egyenessel csak egyetlen metszéspontja van – ettől lesz függvény). Ezek után adjuk meg a grafikonhoz függvény egyenletét. Természetesen a pontok koordinátái és a szakaszok meredeksége megállapítható a grafikonból. A megoldás:

1. Állapítsuk meg a grafikonból az M_i meredekségeket.

2. Az M_i -k segítségével határozzuk meg az m_i és az m együtthatókat a fentebbi összefüggések alapján.

3. A töréspontok x koordinátáinak negatívja adja a b_i értékeket.

4. A b meghatározásához helyettesítsük be egy pontnak a koordinátáit a függvény képletébe, majd átrendezéssel az értéke adódik. Ha például a függvény az y tengelyt a h₀ -ban metszi, akkor a képlet utolsó elemét így számíthatjuk ki:

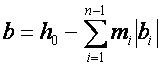
Eddig csak elsőrendű (abszolútértékes-jelet egymásba nem záró) képletekkel megadott abszolút-értékes függvényekkel foglalkoztunk. Nézzük mi a helyzet a magasabb rendű függvényekkel. Egészítsük ki a programot az ilyen függvények rajzolási lehetőségével. Ábrázoljunk a következő másodrendű függvényt:

Íme a képe:

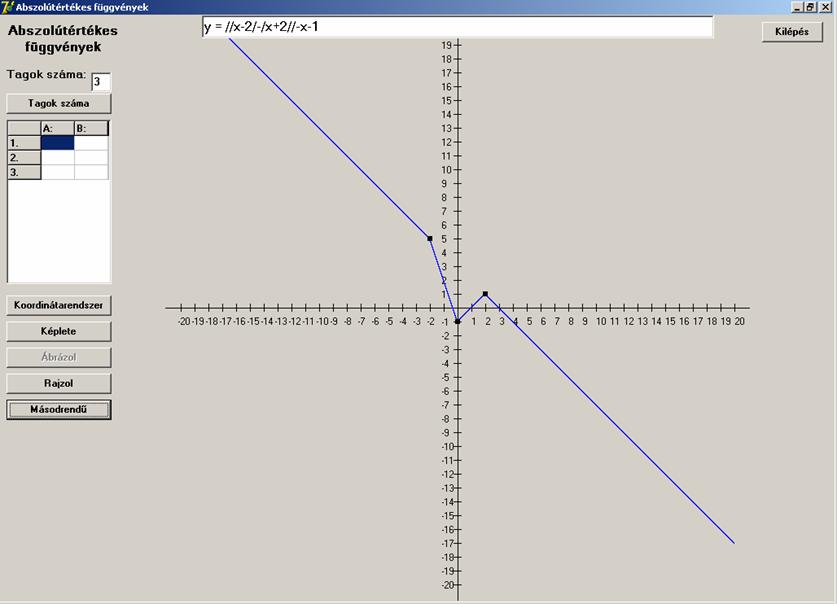
Vegyünk egy harmadrendűt:

Ábrázoljuk:

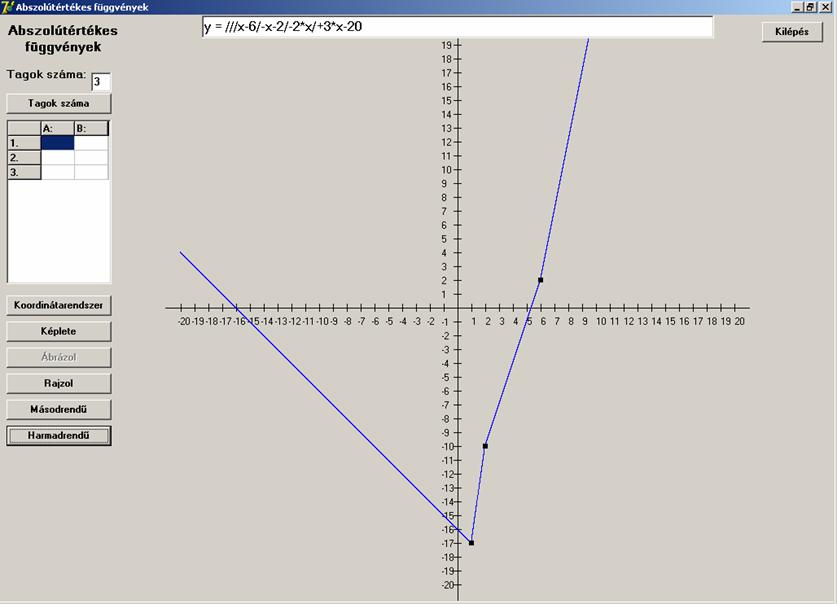
Azt mondhatnám, hogy semmi extra. Újra törött vonalakat kaptunk. Most alkalmazzuk az előbb leírt módszert, amikor a függvény képéből felírjuk a függvény egyenletét (képletét). Ez utóbbi, harmadrendű függvénynek három töréspontja van. Töréspontjai: (1, -17), (2, -10) és (6, 2). Tengelymetszete: (0, -16). Meredekségek: M₁ = -1, M₂ = 7, M₃ = 3 és M₄ = 5. A fenti képletek alapján:

Ezek alapján ennek a függvénynek az elsőrendű alakja:

Következmény:

Amit ábrázolás nélkül ki nem találtunk volna. Ábrázoljuk a most kapott elsőrendű függvényt is.

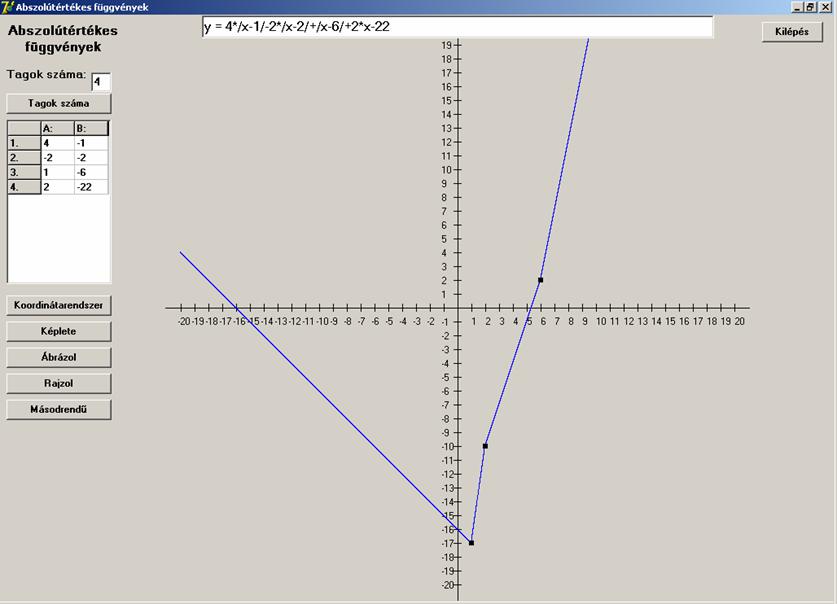
Látható, hogy teljesen egyezik a harmadrendűvel. Hasonlóan járhatunk el a fentebbi, másodrendű függvénnyel is. A függvény képéből írjuk fel az elsőrendű alakját. Annak a töréspontjai: (-2, 5), (0, -1) és (2, 1). Tengelymetszete: (0, -1). A meredekségek: M₁ = -1, M₂ = -3, M₃= 1 és M₄ = -1. Az elsőrendű alak meredekségei: m₁ = -1, m₂ = 2, m₃ = -1 és m = -1. A konstans értéke: b = -1-(-1*2+2*0-1*2) = -1-(-4) = -1+4 = 3. Azaz az elsőrendű alak:

Ellenőrzésképpen ezt is ábrázoljuk:

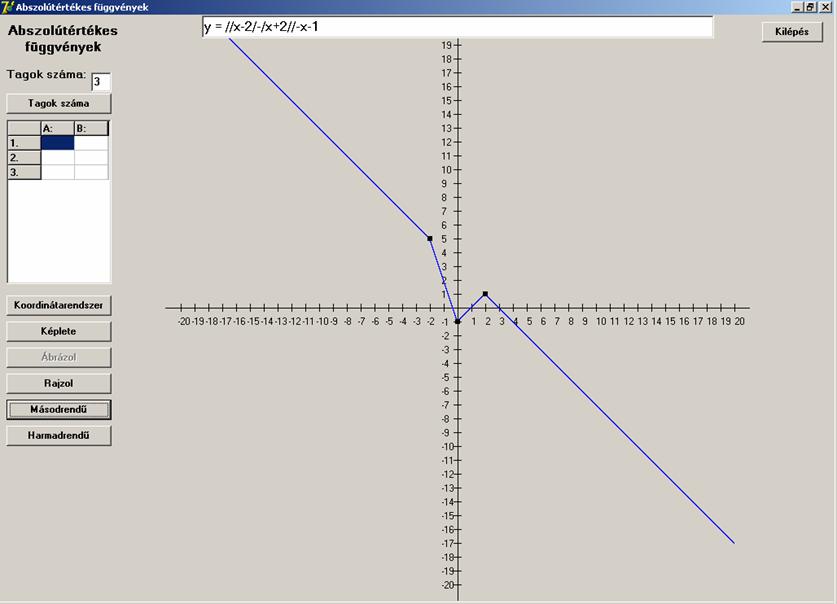
Teljes az egyezés, azaz:

Ezek után azt mondhatjuk, hogy szerencsés volt csak az elsőrendű függvényekkel foglalkozni részletesebben, mert minden magasabb rendűnek van elsőrendű alakja is.

A következő részben implicit abszolút-értékes függvényekkel foglalkozom.