Nyerő négyzet

Írjunk az amőbához hasonló játékprogramot, amelyben a cél az, hogy jeleinket egy négyzet csúcsaiban kell elhelyezni. A négyzet elhelyezkedése nemcsak tengelyirányú lehet, azaz az oldalai akár L alakban is elhelyezkedhetnek a rácshoz képest.

A program írja ki a képernyőre a szabályokat:

- az X gép jele, és a gép kezdi a játékot,

- az O a játékos jele,

- a gép és a játékos felváltva helyezik el jelüket a rácson,

- az nyer, akinek 4 jele egy négyzet négy csúcsában helyezkedik el,

- a négyzet oldali nem feltétlen párhuzamosak a rácsrendszer soraival, oszlopaival.

A gép valamilyen algoritmus szerint találjon maga számára célravezető lépéseket. Legyen védekező és némi támadó stratégiája. A játék csak a megadott keretek között folytatódhat. Bármikor meg lehessen szakítani a játékot (Kilépés). Lehessen új játékot kérni. Ha véget ér a játék, az eredményt írja a képernyőre: Győztem, Győztél. A nyerő jelsorozatot vörös színnel jelenítse meg.

A program egy futtatási képe:

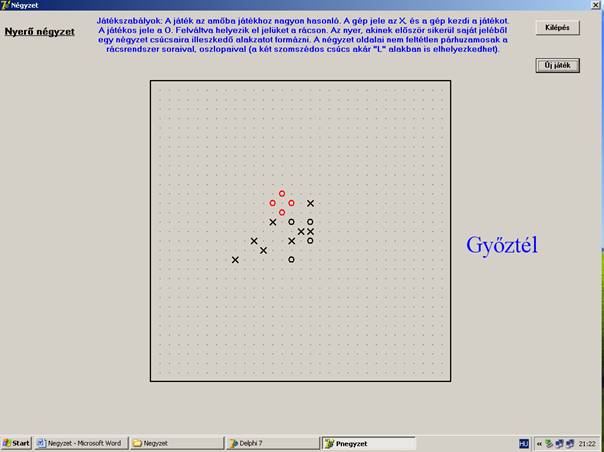
A program listája:

unit UNegyzet;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes,

Graphics, Controls, Forms, Dialogs, StdCtrls;

type
  TfmNegyzet = class(TForm)
    lbNegyzet: TLabel;
    lbSzabaly: TLabel;
    btKilepes: TButton;
    btUjJatek: TButton;
Procedure Kepre;
Function Vege: Byte;
Procedure Gep;
procedure FormPaint(Sender: TObject);
procedure btKilepesClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure FormMouseMove(Sender: TObject; Shift: TShiftState; X,
      Y: Integer);
procedure FormClick(Sender: TObject);
procedure btUjJatekClick(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

Const Max=31;
      D=16;
      Dx=8;
      Dy=8;
      R=5;

var
  fmNegyzet: TfmNegyzet;
  Xk, Yk, Mx, My, F: Integer;
  Mezo: Array[0..Max+1,0..Max+1] Of Byte;
  VegeVan: Byte;

implementation

{$R *.dfm}

procedure TfmNegyzet.btKilepesClick(Sender: TObject);
begin
  Close;
end;

procedure TfmNegyzet.FormCreate(Sender: TObject);
begin
  Canvas.Brush.Color:= clBtnFace;
  Randomize;
end;

procedure TfmNegyzet.FormPaint(Sender: TObject);
Var I, J: Integer;
begin
  Xk:= ClientWidth Div 2;
  Yk:= ClientHeight Div 2;
With Canvas Do
Begin
    F:= Max Div 2;
With Canvas Do
Begin
With Pen Do
Begin
        Color:= clBlack;
        Width:= 2;
End;
      Rectangle(Xk-(F+1)*D,Yk-(F+1)*D, Xk+(F+1)*D,Yk+(F+1)*D);
For I:= -F To F Do For J:= -F To F Do
      Pixels[Xk+I*D, Yk+J*D]:= 0;
End;
    Mezo[F+1,F+1]:= 1;
    Kepre;
End;
end;

Procedure TfmNegyzet.Kepre;
Var I, J: Integer;
Begin
For I:= -F To F Do For J:= -F To F Do With Canvas Do
Begin
With Pen Do
Case Mezo[I+F+1,J+F+1] Of
      1,2: Color:= clBlack;
      3,4: Color:= clRed;
End;
Case Mezo[I+F+1,J+F+1] Of
      1,3: Begin
MoveTo(Xk+I*D-R,Yk+J*D-R);
             LineTo(Xk+I*D+R,Yk+J*D+R);
             MoveTo(Xk+I*D-R,Yk+J*D+R);
             LineTo(Xk+I*D+R,Yk+J*D-R);
End;
      2,4: Ellipse(Xk+I*D-R,Yk+J*D-R,Xk+I*D+R,Yk+J*D+R);
End;
End;
End;

procedure TfmNegyzet.FormMouseMove(Sender: TObject; Shift: TShiftState; X,
  Y: Integer);
begin
  Mx:= X; My:= Y;
end;

procedure TfmNegyzet.FormClick(Sender: TObject);
begin
If VegeVan<>0 Then Exit;
If (Mx<Xk-F*D) Or (Mx>Xk+F*D) Or
     (My<Yk-F*D) Or (My>Yk+F*D) Then Exit;
If Mezo[(Mx-Xk+(F+1)*D+Dx) Div D,(My-Yk+(F+1)*D+Dy) Div D]<>0 Then Exit;
With Canvas Do
Begin
With Font Do
Begin
      Name:= 'Times New Roman';
      Size:= 30;
      Color:= clBlue;
End;
    Mezo[(Mx-Xk+(F+1)*D+Dx) Div D,(My-Yk+(F+1)*D+Dy) Div D]:= 2;
Case Vege Of
      1: TextOut(Xk+(F+2)*D,Yk,' Győztem ');
      2: TextOut(Xk+(F+2)*D,Yk,' Győztél ');
End;
    Kepre;
If VegeVan=0 Then
Begin
      Gep;
Case Vege Of
        1: TextOut(Xk+(F+2)*D,Yk,' Győztem ');
        2: TextOut(Xk+(F+2)*D,Yk,' Győztél ');
End;
      Kepre;
End;
End;
end;

Function TfmNegyzet.Vege: Byte;
Var I, J, N, M, V: Word;
Begin
Vege:= 0; VegeVan:= 0;
For I:= 1 To Max Do For J:= 1 To Max Do If Mezo[I,J]<>0 Then
Begin
    V:= Max-I; If Max-J<V Then V:= Max-J;
For N:= 1 To V Do For M:= 0 To V Do
If ((I+N-M)>0) And ((I-M)>0) Then
If (Mezo[I,J]=Mezo[I+N  ,J  +M]) And
       (Mezo[I,J]=Mezo[I+N-M,J+N+M]) And
       (Mezo[I,J]=Mezo[I  -M,J+N  ]) Then
Begin
      Vege:= Mezo[I,J]; VegeVan:= Mezo[I,J];
      Inc(Mezo[I,    J    ],2);
      Inc(Mezo[I+N  ,J  +M],2);
      Inc(Mezo[I+N-M,J+N+M],2);
      Inc(Mezo[I  -M,J+N  ],2);
      Break;
End;
End;
End;

Procedure TfmNegyzet.Gep;
Var I, J, N, M, P, Q, R, V, Z: Word;
Begin
For I:= 1 To Max Do For J:= 1 To Max Do
Begin
    V:= Max-I; If Max-J<V Then V:= Max-J;
For N:= 1 To V Do For M:= 0 To V Do
If ((I+N-M)>0) And ((I-M)>0) Then
Begin
      P:= 0; Q:= 0; R:= 0; Z:= 0;
If Mezo[I,J]=0 Then Begin Inc(R); Z:= 1 End;
If Mezo[I,J]=1 Then Inc(P);
If Mezo[I,J]=2 Then Inc(Q);
If Mezo[I+N  ,J  +M]=0 Then Begin Inc(R); Z:= 2 End;
If Mezo[I+N  ,J  +M]=1 Then Inc(P);
If Mezo[I+N  ,J  +M]=2 Then Inc(Q);
If Mezo[I+N-M,J+N+M]=0 Then Begin Inc(R); Z:= 3 End;
If Mezo[I+N-M,J+N+M]=1 Then Inc(P);
If Mezo[I+N-M,J+N+M]=2 Then Inc(Q);
If Mezo[I  -M,J+N  ]=0 Then Begin Inc(R); Z:= 4 End;
If Mezo[I  -M,J+N  ]=1 Then Inc(P);
If Mezo[I  -M,J+N  ]=2 Then Inc(Q);
If (R=1) And ((P=3) Or (Q=3)) Then
Begin
Case Z Of
          1: Mezo[I,J]:= 1;
          2: Mezo[I+N  ,J  +M]:= 1;
          3: Mezo[I+N-M,J+N+M]:= 1;
          4: Mezo[I  -M,J+N  ]:= 1;
End;
        Exit;
End;
End;
End;

For I:= 1 To Max Do For J:= 1 To Max Do
Begin
    V:= Max-I; If Max-J<V Then V:= Max-J;
For N:= 1 To V Do For M:= 0 To V Do
If ((I+N-M)>0) And ((I-M)>0) Then
Begin
      P:= 0; Q:= 0; R:= 0; Z:= 0;
If Mezo[I,J]=0 Then Begin Inc(R); Z:= 1 End;
If Mezo[I,J]=1 Then Inc(P);
If Mezo[I,J]=2 Then Inc(Q);
If Mezo[I+N  ,J  +M]=0 Then Begin Inc(R); Z:= 2 End;
If Mezo[I+N  ,J  +M]=1 Then Inc(P);
If Mezo[I+N  ,J  +M]=2 Then Inc(Q);
If Mezo[I+N-M,J+N+M]=0 Then Begin Inc(R); Z:= 3 End;
If Mezo[I+N-M,J+N+M]=1 Then Inc(P);
If Mezo[I+N-M,J+N+M]=2 Then Inc(Q);
If Mezo[I  -M,J+N  ]=0 Then Begin Inc(R); Z:= 4 End;
If Mezo[I  -M,J+N  ]=1 Then Inc(P);
If Mezo[I  -M,J+N  ]=2 Then Inc(Q);
If (R=2) And ((P=2) Or (Q=2)) Then
Begin
Case Z Of
          1: Mezo[I,J]:= 1;
          2: Mezo[I+N  ,J  +M]:= 1;
          3: Mezo[I+N-M,J+N+M]:= 1;
          4: Mezo[I  -M,J+N  ]:= 1;
End;
        Exit;
End;
End;
End;
Repeat
    I:= Random(Max)+1;
    J:= Random(Max)+1;
Until (Mezo[I,J]=0) And
        (Mezo[I-1,J-1]+Mezo[I  ,J-1]+Mezo[I+1,J-1]+
         Mezo[I-1,J  ]+              Mezo[I+1,J  ]+
         Mezo[I-1,J+1]+Mezo[I  ,J+1]+Mezo[I+1,J+1]>0);
  Mezo[I,J]:= 1;
//(0,0); (n,0);(n,n);(0,n); (0,1);(-1,1);(-1,0)
End;

procedure TfmNegyzet.btUjJatekClick(Sender: TObject);
Var I, J: Integer;
begin
For I:= 0 To Max+1 Do For J:= 0 To Max+1 Do Mezo[I,J]:= 0;
  VegeVan:= 0;
With Canvas Do
Begin
    Pen.Color:= clBtnFace;
    Brush.Color:= clBtnFace;
    Rectangle(Xk+(F+2)*D,Yk,Xk+(F+13)*D,Yk+3*D);
End;
  FormPaint(Sender);
end;

end.