Fakocka
Egy rokoni látogatás alkalmával akadt a kezembe egy fakocka, amely gyakorlatilag egy doboz volt, melynek a tömör belsejét kisebb kockákra illetve hasábokra vágták szét (a játékot a NET-en ördöglakat kategóriába is besorolják). Én gyanútlanul kiborítottam az egészet és megpróbáltam visszarakni, úgy ahogy eredetileg volt, azaz hézagmentesen és szabályos, teljes kitöltéssel. Mondanom sem kell, nem sikerült. Azért, hogy mindenki számára egyértelmű legyen, hogy milyen játékról is beszélek, lefényképeztem összerakott állapotban is és kiszedve a nagy kockából a kisebb elemeket. Íme:

Összerakott fakocka

Szétszedett állapot
Mielőtt továbblépnénk, végezzünk egy kis számvetést. A képekről kiderül, hogy a teljes kocka belső éle 5 egységnyinek tekinthető, azaz a térfogata 125 térfogategység. Nézzük, hogyan jön ez össze a kisebb elemekből:
|
1*1*1 |
kocka |
5 db |
5*1 |
5 térfogategység |
|
1*2*4 |
hasáb |
6 db |
6*8 |
48 térfogategység |
|
2*2*3 |
hasáb |
6 db |
6*12 |
72 térfogategység |
|
Összesen: |
17 db |
|
125 térfogategység |
|
Láthatjuk, hogy a számvetés eredményes. A kis kockák és hasábok térfogatának összege a nagy kocka térfogatával megegyezik, azaz elvileg (de az első képre tekintve látható, hogy gyakorlatilag sincs) nincs semmi akadálya a hézagmentes visszarakásnak. Mivel többszöri próbálkozásomra sem sikerült a kockát eredeti állapota szerint összerakni, arra gondoltam, írok rá programot, ami majd megkeresi a helyes elrendezést.
Első gondolat: szisztematikusan keresse meg a megoldást, az összes eset végigjárásával. Ehhez határozzuk meg, hogy hányféleképpen helyezhetjük a kisebb elemeket a nagy kockába. Az összes lehetséges elhelyezések számát a következő szorzat adja:
(125/1)*(124/2)*…*(121/5)*(120/1)*(119/2)*…*(115/6)*(114/1)*(113/2)*…*(109/6)* 36*66
A 125 helyből először ki kell választani 17-et, majd az 5+6+6-féle elemet ezeken el kell helyezni, ugyanakkor azt is figyelembe kell venni, hogy a kis kockákat egyféleképpen, a hasábokat viszont 3- illetve 6-féle pozícióban helyezhetjük a tér kiválasztott pontjába. A képlet első része a 125 alatt a 17 (azaz 125 elemnek a 17-ed osztályú ismétlés nélküli kombinációja) és a 17 elemnek az ismétléses (5-6-6) permutációja szorzatának egyszerűsítése. A második részben azt vettük figyelembe, hogy az egyikféle (2*2*3-ast) 6 darab hasábot 3-, a másik 6 darabot (az 1*2*4-est) 6-féleképen helyezhetjük a tér egy adott pontjába (csak pozitív koordinátájú elhelyezéssel számoltunk). Készítsünk ennek kiszámítására egy kis Excel táblázatot:
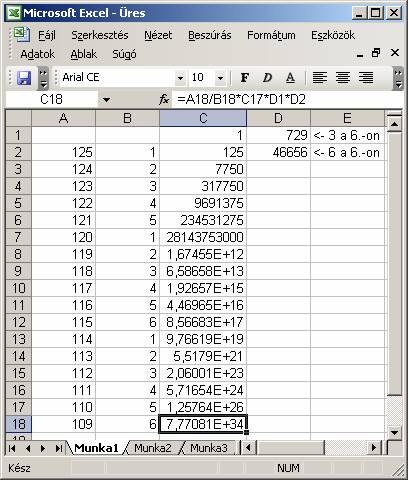
A C oszlopot a C2 húzásával töltöttük fel, melynek tartalma: =A2/B2*C1. Majd a szerkesztőlécben látható módon a C18-at módosítottuk. Azt kaptuk, hogy az összes esetek száma valamivel több, mint egy nagyságrenddel megközelíti a milliárd negyedik hatványát! Ennyi esetet (mert mi van, ha csak az utolsó lépésekben kapjuk meg a megoldást) a mai számítógépekkel végignézni lehetetlen, pontosabban túlságosan hosszú ideig tartana.
Második gondolat: próbáljuk megkeresni a megoldást – a sokszor már eredményesnek bizonyult – ütközésmentesítő algoritmussal. Ez az algoritmus egy olyan genetikus algoritmus, amelynek csak egyetlen egyede van, nincs benne keresztezés, csak két egymás után létrejött egyed között van szelekció, van viszont mutáció. Az algoritmus menete a következő:
– az állapottérben felveszünk egy darab egyedet, véletlen elemekkel,
– egy függvénnyel megállapítjuk az egyed jóságát (hibapontjainak vagy ütközéseinek számát),
– véletlenül kiválasztjuk az egyed egy elemét és megjegyezzük a választást a hibaponttal együtt,
– véletlen értékre megváltoztatjuk a kiválasztott elemet (mutáció),
– újra megállapítjuk az egyed jóságát és megjegyezzük,
– ha az új hibaszám nem rosszabb az előzőnél, akkor a véletlen választást megtartjuk, ha rosszabb, akkor az elem értékét az előzőre visszaállítjuk (szelekció),
– a mutációt és szelekciót addig folytatjuk (áttérünk a következő generációra), amíg vagy 0 hibát nem kapunk (megoldottuk a feladatot), vagy egy előre adott generációszámot el nem érünk.
Ha arra gondolunk, hogy gyakorlatilag csak egyetlen megoldás keresünk a sok-sok milliárd közül (elvileg 24 van, de ezek egymás transzformáltjai), akkor túlságosan gyors eredményre nem számíthatunk. A paramétereket, amelyek a megengedett hibaszám ismétléseit jelentik, illetve az összes lépések számát elég magasan, milliós illetve milliárdos nagyságrendben kell majd keresni. Ehhez persze elég gyors gépre is szükség lesz, hogy értelmes idő alatt megoldás szülessen.
A következő táblázatban a paraméterek 100.000.000 lépés alapján alakultak ki úgy, hogy minden hibaértékre ugyanaz az Ismétlések maximuma:
|
Ismétlés maximuma |
Legjobb |
Hiba maximuma |
Változás maximuma |
Újra |
|
10.000 |
11 / 1 db |
34 |
9.999 |
16.231 |
|
50.000 |
4 / 1 db |
14 |
49.936 |
934 |
|
100.000 |
4 / 8 db |
12 |
99.575 |
520 |
|
200.000 |
4 / 7 db |
10 |
198.372 |
285 |
|
500.000 |
4 / 4 db |
10 |
499.954 |
136 |
|
1.000.000 |
4 / 5 db |
10 |
974.700 |
72 |
|
2.000.000 |
4 / 4 db |
6 |
1.805.416 |
39 |
|
3.000.000 |
4 / 3 db |
6 |
1.887.272 |
29 |
|
5.000.000 |
4 / 1 db |
6 |
4.140.705 |
16 |
Egy kis értelmezés:
Ismétlések maximuma: maximálisan ennyiszer ismétlődhetett egy hibaszám, ha ezt elérte, akkor teljesen új véletlen egyedet generált. Mivel a legjobbnak látszó beállítás a 100000 volt, a legtöbb esetben ezzel a paraméterrel futtattam a programot.
Legjobb: mekkora volt a legjobb elrendezés hibaszáma és hány darabolt állított elő belőle.
Hiba maximuma: amely hibaszám a legtöbbször szerepelt a generálás során.
Változás maximuma: amikor ugyanolyan hibaszám mellett az eljárás keres megoldást, előfordult hogy például 3 milliós maximum esetén 1.887.272 lépés után talált olyat, ami jobb megoldást jelentett és cserélt egyedet a program.
Újra: ennyiszer generált teljesen új elemet a program a teljes futási idő alatt.
Néhány futtatási kép:
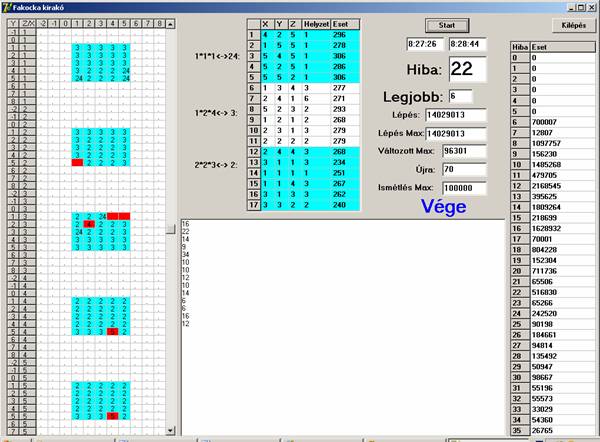
Magyarázat:
A baloldali rácsban a nagy kocka öt szelete látható Z=1-től Z=5-ig.
A zöldeskék területen lévő számok jelentése: 24 – egységkocka helye, 3 – 1*2*4-es hasáb, 2 – 2*2*3-as hasáb helye.
Piros háttérrel rendelkező számok jelentése: olyan számok, amelyek nem esnek a [2,3,24] halmazba, illetve üres a mező. A piros mezők száma az egyed hibapontjainak a száma.
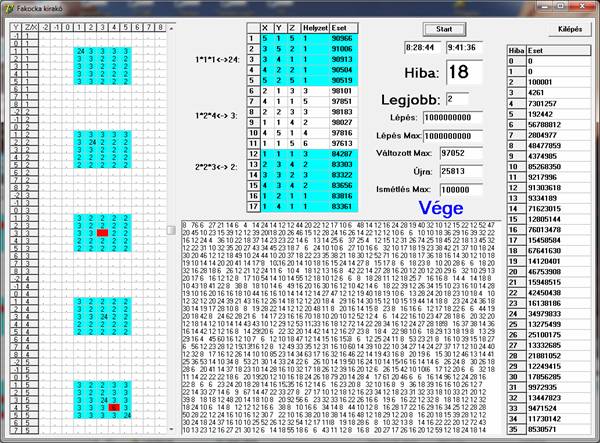
Ezen a képernyőn a milliárdnyi lépés után sem talált megoldást a program. A két hibapont egy üres helyből és egy kettős átfedésből adódik. Az X=3, Y=3 és Z=3 hely üres, az X=4, Y=4 és Z=5 helyen két 3-as kódú hasáb ütközése található. A középső rácsban az aktuális elhelyezkedést és helyzeteket látjuk és azt, hogy hány Esetben szerepelt a kérdéses elem eredményes cserében.

Ezen a képernyőn egy eredményes futtatást láthatunk, mely kb. 6 percig tartott. A baloldali rácsban nincs piros mező. A legjobb érték közvetlenül a megoldás megtalálása előtt 2 hibapont volt. A jobboldali rácsban azt láthatjuk, hogy az egyes hibapont értékek a teljes futási idő alatt hányszor fordultak elő. Megjegyezném, hogy a páratlan hibapontok száma sokkal kisebb, mint a párosoké. A középső nagy listadobozban a milliónkénti aktuális hibapontok láthatók.
A megoldásból az ügyesebbeknek csak annyit kell megjegyezni, hogy a kis kockák a megoldásban a nagy kocka testátlójában foglalnak helyet. Ha ennek tudatában végezzük az összerakást, akkor van remény arra, hogy a gépi eredmény elemzése nélkül is sikerül.
Akiknek még így is nehéz feladat a kocka összerakása, segítségül egy másik programban a megoldást géppel, axonometriában megrajzoltattam. Ebből is néhány screenshot:
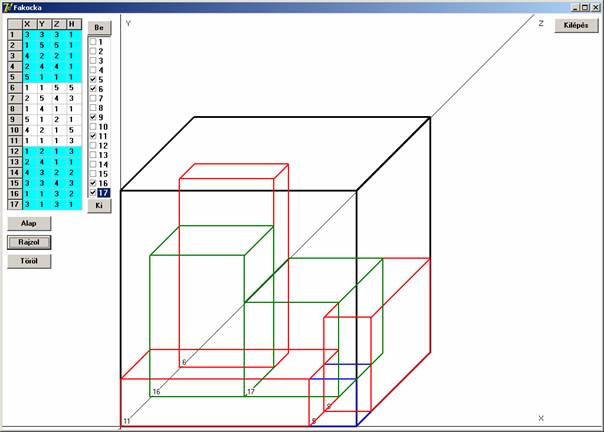
A kocka alsólapján (az X-Z síkon) nyugvó elemek
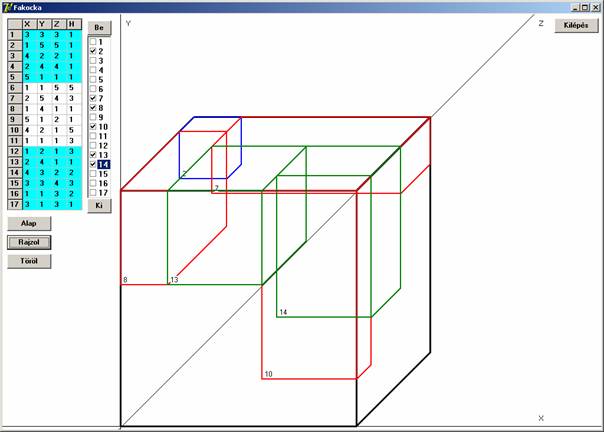
A kocka felső (az X-Z síkkal párhuzamos) lapján nyugvó elemek
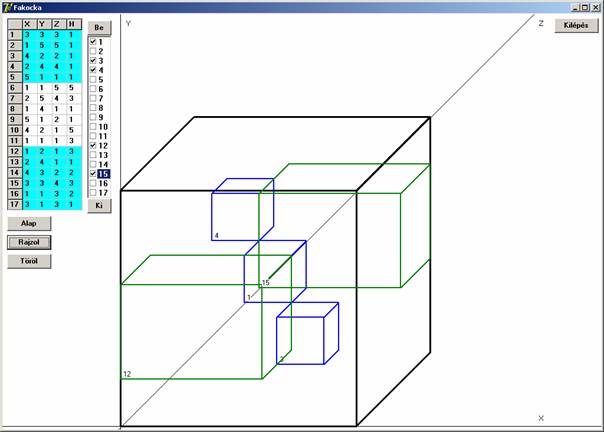
Azok az elemek (belsők), amelyek az előző két elrendezésből kimaradtak
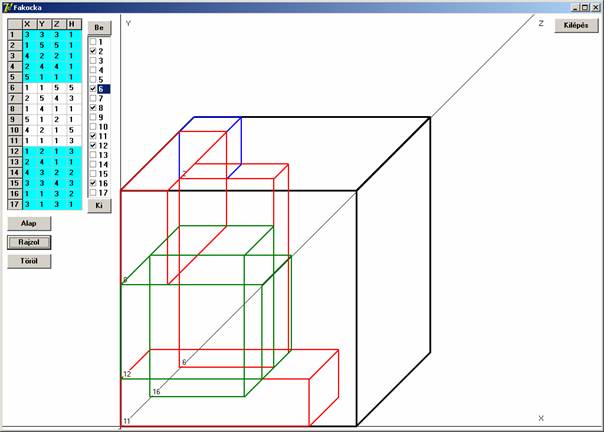
A kocka baloldali lapján (az Y-Z síkon) nyugvó elemek

A kocka jobboldali (az Y-Z síkkal párhuzamos) lapján nyugvó elemek
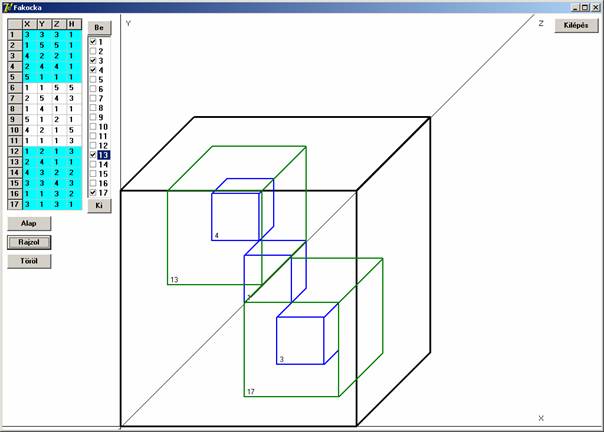
Azok az elemek (belsők), amelyek az előző két elrendezésből kimaradtak
Íme a kockakirakó program listája:
(* 1*1*1 = 1 5*1 = 5 Index: 1 - 5 Helyzet: 1 Azonositó: 24
1*2*4 = 8 6*8 = 48 Index: 6 - 11 Helyzet: 1 - 6 Azonositó: 3
2*2*3 = 12 6*12 = 72 Index: 12 - 15 Helyzet: 1 - 3 Azonositó: 2
--------------------
Osszesen: 125
**)
unit UFKK;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Grids;
Const VH1=6;
VH2=3;
type
TfmFKK = class(TForm)
btKilepes: TButton;
sgMoni: TStringGrid;
lbKesz: TLabel;
edHiba: TEdit;
edBest: TEdit;
sgElem: TStringGrid;
lbHiba: TLabel;
btStart: TButton;
edLSz: TEdit;
edStart: TEdit;
edStop: TEdit;
ldHelp: TListBox;
lbElso: TLabel;
lbMasod: TLabel;
lbHarmad: TLabel;
edUjra: TEdit;
edMValt: TEdit;
sgIsm: TStringGrid;
lbBest: TLabel;
lbLSz: TLabel;
lbValtMax: TLabel;
lbUjra: TLabel;
edMax: TEdit;
lbMax: TLabel;
lbIMax: TLabel;
edIMax: TEdit;
Procedure UresTer;
Procedure ElemDel(N: Word);
Procedure ElemTerbe(N: Word);
Procedure Kepre;
Procedure ElemMake(N,IH: Word);
Procedure General;
Function Utkozesek: Word;
procedure btKilepesClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure sgMoniDrawCell(Sender: TObject; ACol, ARow: Integer;
Rect: TRect; State: TGridDrawState);
procedure btStartClick(Sender: TObject);
procedure sgElemDrawCell(Sender: TObject; ACol, ARow: Integer;
Rect: TRect; State: TGridDrawState);
procedure edMaxChange(Sender: TObject);
procedure edIMaxChange(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
TElem=Record
X, Y, Z: Integer; //kezdohely
H: Word; //helyzet
Eset: LongInt; //eredmenyes cserek szama
End;
var
fmFKK: TfmFKK;
Ter: Array[-2..8,-2..8,-2..8] Of Word;
ElemT, BT: Array[0..17] Of TElem;
Kezd, RKezd: Word;
IsmT: Array[0..35] Of Int64;
Max: Int64;
IMax, PMax: LongInt;
implementation
{$R *.dfm}
procedure TfmFKK.btKilepesClick(Sender: TObject);
begin
Close;
end;
procedure TfmFKK.sgMoniDrawCell(Sender: TObject; ACol, ARow: Integer;
Rect: TRect; State: TGridDrawState);
begin
With sgMoni.Canvas.Brush Do
Begin
If Not((gdSelected In State) Or (gdFixed In State)) Then
Begin
If (StrToInt(sgMoni.Cells[0,ARow])>0) And
(StrToInt(sgMoni.Cells[0,ARow])<6) And
(StrToInt(sgMoni.Cells[1,ARow])>0) And
(StrToInt(sgMoni.Cells[1,ARow])<6) And (ACol>4) And (ACol<10) Then
Color:= clAqua Else Color:= clWindow;
If (StrToInt(sgMoni.Cells[0,ARow])>0) And
(StrToInt(sgMoni.Cells[0,ARow])<6) And
(StrToInt(sgMoni.Cells[1,ARow])>0) And
(StrToInt(sgMoni.Cells[1,ARow])<6) And (ACol>4) And (ACol<10) And
(sgMoni.Cells[ACol,ARow]<>'2') And
(sgMoni.Cells[ACol,ARow]<>'3') And
(sgMoni.Cells[ACol,ARow]<>'24') Then
Color:= clRed;
End;
If (gdSelected In State) Then Color:= clYellow;
End;
sgMoni.Canvas.TextRect(Rect,Rect.Left+6,Rect.Top,sgMoni.Cells[ACol,ARow]);
If gdFocused In State Then sgMoni.Canvas.DrawFocusRect(Rect);
end;
procedure TfmFKK.sgElemDrawCell(Sender: TObject; ACol, ARow: Integer;
Rect: TRect; State: TGridDrawState);
begin
With sgElem.Canvas.Brush Do
Begin
If Not((gdSelected In State) Or (gdFixed In State)) Then
If (ARow In [1..5]) Or (ARow In [12..17]) Then
Color:= clAqua Else Color:= clWindow;
If (gdSelected In State) Then Color:= clYellow;
End;
sgElem.Canvas.TextRect(Rect,Rect.Left+3,Rect.Top+1,sgElem.Cells[ACol,ARow]);
If gdFocused In State Then sgElem.Canvas.DrawFocusRect(Rect);
end;
procedure TfmFKK.FormCreate(Sender: TObject);
Var I,J: Integer;
begin
Randomize; Kezd:=1; RKezd:=17;
Max:= StrToInt(edMax.Text); IMax:= StrToInt(edIMax.Text); PMax:= IMax;
With sgMoni Do
Begin
ColWidths[1]:= 28; RowHeights[0]:= 14;
Cells[0,0]:= 'Y'; Cells[1,0]:= 'Z/X';
For I:= -2 To 8 Do Cells[I+4,0]:= IntToStr(I);
For I:= -2 To 8 Do For J:= -2 To 8 Do Cells[0,(I+2)*11+J+3]:= IntToStr(J);
For I:= -2 To 8 Do For J:= -2 To 8 Do Cells[1,(I+2)*11+J+3]:= IntToStr(I);
RowHeights[RowCount-1]:= 0; Row:= RowCount-1;
End;
With sgElem Do
Begin
ColWidths[ColCount-1]:= 48;
ColWidths[4]:= 48;
Cells[1,0]:= 'X'; Cells[2,0]:= 'Y'; Cells[3,0]:= 'Z';
Cells[4,0]:= 'Helyzet';
For I:= 1 To 17 Do Cells[0,I]:= IntToStr(I); Cells[ColCount-1,0]:= 'Eset';
RowHeights[RowCount-1]:= 0; Row:= RowCount-1;
End;
With sgIsm Do
Begin
ColWidths[0]:= 32;
Cells[0,0]:= 'Hiba'; Cells[1,0]:= 'Eset';
For I:= 0 To 35 Do Cells[0,I+1]:= IntToStr(I);
RowHeights[RowCount-1]:= 0; Row:= RowCount-1;
End;
UresTer; For I:= 1 To 17 Do ElemT[I].Eset:= 0; Kepre;
end;
Procedure TfmFKK.UresTer;
Var I, J, K: Integer;
Begin
For I:= -2 To 8 Do For J:= -2 To 8 Do For K:= -2 To 8 Do Ter[I,J,K]:= 0;
End;
Procedure TfmFKK.ElemDel(N: Word); //N. elemet kiveszi a terbol
Var D: Word;
Begin
With ElemT[N] Do
Case N Of
1..5: Begin
D:= 24;
Dec(Ter[X,Y,Z],D);
End;
6..11: Begin //1*2*4
D:= 3;
Case H Of
1: Begin //1-2-4
Dec(Ter[X, Y, Z ],D); Dec(Ter[X, Y+1,Z ],D);
Dec(Ter[X, Y, Z+1],D); Dec(Ter[X, Y+1,Z+1],D);
Dec(Ter[X, Y, Z+2],D); Dec(Ter[X, Y+1,Z+2],D);
Dec(Ter[X, Y, Z+3],D); Dec(Ter[X, Y+1,Z+3],D);
End;
2: Begin //1-4-2
Dec(Ter[X, Y, Z ],D); Dec(Ter[X, Y, Z+1],D);
Dec(Ter[X, Y+1,Z ],D); Dec(Ter[X, Y+1,Z+1],D);
Dec(Ter[X, Y+2,Z ],D); Dec(Ter[X, Y+2,Z+1],D);
Dec(Ter[X, Y+3,Z ],D); Dec(Ter[X, Y+3,Z+1],D);
End;
3: Begin //4-1-2
Dec(Ter[X, Y, Z ],D); Dec(Ter[X, Y, Z+1],D);
Dec(Ter[X+1,Y, Z ],D); Dec(Ter[X+1,Y, Z+1],D);
Dec(Ter[X+2,Y, Z ],D); Dec(Ter[X+2,Y, Z+1],D);
Dec(Ter[X+3,Y, Z ],D); Dec(Ter[X+3,Y, Z+1],D);
End;
4: Begin //2-1-4
Dec(Ter[X, Y, Z ],D); Dec(Ter[X+1,Y, Z ],D);
Dec(Ter[X ,Y, Z+1],D); Dec(Ter[X+1,Y, Z+1],D);
Dec(Ter[X ,Y, Z+2],D); Dec(Ter[X+1,Y, Z+2],D);
Dec(Ter[X ,Y, Z+3],D); Dec(Ter[X+1,Y, Z+3],D);
End;
5: Begin //2-4-1
Dec(Ter[X, Y, Z ],D); Dec(Ter[X+1,Y, Z ],D);
Dec(Ter[X, Y+1,Z ],D); Dec(Ter[X+1,Y+1,Z ],D);
Dec(Ter[X, Y+2,Z ],D); Dec(Ter[X+1,Y+2,Z ],D);
Dec(Ter[X, Y+3,Z ],D); Dec(Ter[X+1,Y+3,Z ],D);
End;
6: Begin //4-2-1
Dec(Ter[X, Y, Z ],D); Dec(Ter[X, Y+1,Z ],D);
Dec(Ter[X+1,Y, Z ],D); Dec(Ter[X+1,Y+1,Z ],D);
Dec(Ter[X+2,Y, Z ],D); Dec(Ter[X+2,Y+1,Z ],D);
Dec(Ter[X+3,Y, Z ],D); Dec(Ter[X+3,Y+1,Z ],D);
End;
End;
End;
12..17: Begin //2*2*3
D:= 2;
Case H Of
1: Begin //2-2-3
Dec(Ter[X, Y, Z ],D); Dec(Ter[X, Y, Z+1],D);
Dec(Ter[X, Y, Z+2],D); Dec(Ter[X+1,Y, Z ],D);
Dec(Ter[X+1,Y, Z+1],D); Dec(Ter[X+1,Y, Z+2],D);
Dec(Ter[X, Y+1,Z ],D); Dec(Ter[X, Y+1,Z+1],D);
Dec(Ter[X, Y+1,Z+2],D); Dec(Ter[X+1,Y+1,Z ],D);
Dec(Ter[X+1,Y+1,Z+1],D); Dec(Ter[X+1,Y+1,Z+2],D);
End;
2: Begin //2-3-2
Dec(Ter[X, Y, Z ],D); Dec(Ter[X, Y+1,Z ],D);
Dec(Ter[X, Y+2,Z ],D); Dec(Ter[X+1,Y, Z ],D);
Dec(Ter[X+1,Y+1,Z ],D); Dec(Ter[X+1,Y+2,Z ],D);
Dec(Ter[X, Y, Z+1],D); Dec(Ter[X, Y+1,Z+1],D);
Dec(Ter[X, Y+2,Z+1],D); Dec(Ter[X+1,Y, Z+1],D);
Dec(Ter[X+1,Y+1,Z+1],D); Dec(Ter[X+1,Y+2,Z+1],D);
End;
3: Begin //3-2-2
Dec(Ter[X, Y, Z ],D); Dec(Ter[X+1,Y, Z ],D);
Dec(Ter[X+2,Y, Z ],D); Dec(Ter[X, Y+1,Z ],D);
Dec(Ter[X+1,Y+1,Z ],D); Dec(Ter[X+2,Y+1,Z ],D);
Dec(Ter[X, Y, Z+1],D); Dec(Ter[X+1,Y, Z+1],D);
Dec(Ter[X+2,Y, Z+1],D); Dec(Ter[X, Y+1,Z+1],D);
Dec(Ter[X+1,Y+1,Z+1],D); Dec(Ter[X+2,Y+1,Z+1],D);
End;
End;
End;
End;
End;
Procedure TfmFKK.ElemMake(N,IH: Word); //N. elemet keszit H helyzetben
Begin
With ElemT[N] Do
Begin
H:= IH;
Case N Of
1..5: Begin X:= Random(11)-2; Y:= Random(11)-2; Z:= Random(11)-2 End;
6..11: Begin X:= Random(8)-2; Y:= Random(8)-2; Z:= Random(8)-2 End;
12..17: Begin X:= Random(9)-2; Y:= Random(9)-2; Z:= Random(9)-2 End;
End;
End;
End;
Procedure TfmFKK.General;
Var I: Word;
Begin
For I:= 1 To 5 Do ElemMake(I,1);
For I:= 6 To 11 Do ElemMake(I,Random(VH1)+1);
For I:= 12 To 17 Do ElemMake(I,Random(VH2)+1);
For I:= 1 To 17 Do ElemTerbe(I);
End;
Procedure TfmFKK.ElemTerbe(N: Word); //N. elemet beteszi a terbe
Var D: Word;
Begin
With ElemT[N] Do
Case N Of
1..5: Begin
D:= 24;
Inc(Ter[X,Y,Z],D);
End;
6..11: Begin //1*2*4
D:= 3;
Case H Of
1: Begin //1-2-4
Inc(Ter[X, Y, Z ],D); Inc(Ter[X, Y+1,Z ],D);
Inc(Ter[X, Y, Z+1],D); Inc(Ter[X, Y+1,Z+1],D);
Inc(Ter[X, Y, Z+2],D); Inc(Ter[X, Y+1,Z+2],D);
Inc(Ter[X, Y, Z+3],D); Inc(Ter[X, Y+1,Z+3],D);
End;
2: Begin //1-4-2
Inc(Ter[X, Y, Z ],D); Inc(Ter[X, Y, Z+1],D);
Inc(Ter[X, Y+1,Z ],D); Inc(Ter[X, Y+1,Z+1],D);
Inc(Ter[X, Y+2,Z ],D); Inc(Ter[X, Y+2,Z+1],D);
Inc(Ter[X, Y+3,Z ],D); Inc(Ter[X, Y+3,Z+1],D);
End;
3: Begin //4-1-2
Inc(Ter[X, Y, Z ],D); Inc(Ter[X, Y, Z+1],D);
Inc(Ter[X+1,Y, Z ],D); Inc(Ter[X+1,Y, Z+1],D);
Inc(Ter[X+2,Y, Z ],D); Inc(Ter[X+2,Y, Z+1],D);
Inc(Ter[X+3,Y, Z ],D); Inc(Ter[X+3,Y, Z+1],D);
End;
4: Begin //2-1-4
Inc(Ter[X, Y, Z ],D); Inc(Ter[X+1,Y, Z ],D);
Inc(Ter[X ,Y, Z+1],D); Inc(Ter[X+1,Y, Z+1],D);
Inc(Ter[X ,Y, Z+2],D); Inc(Ter[X+1,Y, Z+2],D);
Inc(Ter[X ,Y, Z+3],D); Inc(Ter[X+1,Y, Z+3],D);
End;
5: Begin //2-4-1
Inc(Ter[X, Y, Z ],D); Inc(Ter[X+1,Y, Z ],D);
Inc(Ter[X, Y+1,Z ],D); Inc(Ter[X+1,Y+1,Z ],D);
Inc(Ter[X, Y+2,Z ],D); Inc(Ter[X+1,Y+2,Z ],D);
Inc(Ter[X, Y+3,Z ],D); Inc(Ter[X+1,Y+3,Z ],D);
End;
6: Begin //4-2-1
Inc(Ter[X, Y, Z ],D); Inc(Ter[X, Y+1,Z ],D);
Inc(Ter[X+1,Y, Z ],D); Inc(Ter[X+1,Y+1,Z ],D);
Inc(Ter[X+2,Y, Z ],D); Inc(Ter[X+2,Y+1,Z ],D);
Inc(Ter[X+3,Y, Z ],D); Inc(Ter[X+3,Y+1,Z ],D);
End;
End;
End;
12..17: Begin //2*2*3
D:= 2;
Case H Of
1: Begin //2-2-3
Inc(Ter[X, Y, Z ],D); Inc(Ter[X, Y, Z+1],D);
Inc(Ter[X, Y, Z+2],D); Inc(Ter[X+1,Y, Z ],D);
Inc(Ter[X+1,Y, Z+1],D); Inc(Ter[X+1,Y, Z+2],D);
Inc(Ter[X, Y+1,Z ],D); Inc(Ter[X, Y+1,Z+1],D);
Inc(Ter[X, Y+1,Z+2],D); Inc(Ter[X+1,Y+1,Z ],D);
Inc(Ter[X+1,Y+1,Z+1],D); Inc(Ter[X+1,Y+1,Z+2],D);
End;
2: Begin //2-3-2
Inc(Ter[X, Y, Z ],D); Inc(Ter[X, Y+1,Z ],D);
Inc(Ter[X, Y+2,Z ],D); Inc(Ter[X+1,Y, Z ],D);
Inc(Ter[X+1,Y+1,Z ],D); Inc(Ter[X+1,Y+2,Z ],D);
Inc(Ter[X, Y, Z+1],D); Inc(Ter[X, Y+1,Z+1],D);
Inc(Ter[X, Y+2,Z+1],D); Inc(Ter[X+1,Y, Z+1],D);
Inc(Ter[X+1,Y+1,Z+1],D); Inc(Ter[X+1,Y+2,Z+1],D);
End;
3: Begin //3-2-2
Inc(Ter[X, Y, Z ],D); Inc(Ter[X+1,Y, Z ],D);
Inc(Ter[X+2,Y, Z ],D); Inc(Ter[X, Y+1,Z ],D);
Inc(Ter[X+1,Y+1,Z ],D); Inc(Ter[X+2,Y+1,Z ],D);
Inc(Ter[X, Y, Z+1],D); Inc(Ter[X+1,Y, Z+1],D);
Inc(Ter[X+2,Y, Z+1],D); Inc(Ter[X, Y+1,Z+1],D);
Inc(Ter[X+1,Y+1,Z+1],D); Inc(Ter[X+2,Y+1,Z+1],D);
End;
End;
End;
End;
End;
Function TfmFKK.Utkozesek: Word;
Var I, J, K: Integer;
N: Word;
Begin
N:= 0;
For I:= -2 To 8 Do For J:= -2 To 8 Do For K:= -2 To 8 Do
If (I In [1..5]) And (J In [1..5]) And (K In [1..5]) Then
Begin If Not (Ter[I,J,K] In [2,3,24]) Then Inc(N) End Else
Begin If Ter[I,J,K]>0 Then Inc(N,Ter[I,J,K]) End;
Utkozesek:= N;
End;
Procedure TfmFKK.Kepre;
Var I, J, K: Integer;
Begin
With sgMoni Do
Begin
For K:= -2 To 8 Do For I:= -2 To 8 Do For J:= -2 To 8 Do
If Ter[I,J,K]>0 Then Cells[I+4,J+3+(K+2)*11]:= IntToStr(Ter[I,J,K]) Else
Cells[I+4,J+3+(K+2)*11]:= '.';
End;
With sgElem Do For I:= 1 To 17 Do With ElemT[I] Do
Begin
Cells[1,I]:= IntToStr(X); Cells[2,I]:= IntToStr(Y);
Cells[3,I]:= IntToStr(Z); Cells[4,I]:= IntToStr(H);
Cells[5,I]:= IntToStr(Eset);
End;
End;
procedure TfmFKK.btStartClick(Sender: TObject);
Var AE: TElem;
I, A, H, RH, Best: Word;
N: Int64;
Ism, Ujra, MValt: LongInt;
begin
edStart.Text:= TimeToStr(GetTime); lbKesz.Visible:= False;
N:= 0; UresTer; edHiba.Text:= '0'; edBest.Text:= '0';
General; Kepre;
H:= Utkozesek; edHiba.Text:= IntToStr(H);
Best:= 100; Ism:= 0; RH:= 1000; Ujra:= 1; MValt:= 0; RePaint;
While (H>0) And (N<Max) Do
Begin
Case H Of
0..6: IMax:= PMax;
7..12: IMax:= PMax Div 2;
13..18: IMax:= PMax Div 4;
19..24: IMax:= PMax Div 8;
25..30: IMax:= PMax Div 16;
31..36: IMax:= PMax Div 32;
End;
If H<=35 Then Inc(IsmT[H]);
Inc(N);
If RH=H Then Inc(Ism) Else
Begin
If Ism>MValt Then
Begin MValt:= Ism; edMValt.Text:= IntToStr(MValt); edMValt.Repaint End;
Ism:= 0;
End;
RH:= H; If RH<Best Then Begin Best:= RH; BT:= ElemT End;
A:= Random(RKezd)+Kezd; AE:= ElemT[A]; ElemDel(A);
Case A Of
1..5: ElemMake(A,1);
6..11: ElemMake(A,Random(VH1)+1);
12..17: ElemMake(A,Random(VH2)+1);
End;
ElemTerbe(A);
If Utkozesek>RH Then
Begin ElemDel(A); ElemT[A]:= AE; ElemTerbe(A) End Else
Begin H:= Utkozesek; If H<RH Then Inc(ElemT[A].Eset) End;
If Ism=IMax Then //ujrakezdi
Begin
Inc(Ujra); If MValt=IMax Then MValt:= 0; Ism:= 0; UresTer;
General; H:= Utkozesek;
End;
If N Mod 1000000=0 Then //megjelenit
Begin
Kepre;
For I:= 0 To 35 Do sgIsm.Cells[1,I+1]:= IntToStr(IsmT[I]);
edLSz.Text:= IntToStr(N); edHiba.Text:= IntToStr(H);
edBest.Text:= IntToStr(Best);
ldHelp.Items.Add(IntToStr(H)); edUjra.Text:= IntToStr(Ujra);
edMValt.Text:= IntToStr(MValt); RePaint;
End;
End;
H:= Utkozesek; edLSz.Text:= IntToStr(N); edHiba.Text:= IntToStr(H);
edBest.Text:= IntToStr(Best); Kepre;
If H>0 Then
Begin
UresTer; ElemT:= BT; For I:= 1 To 17 Do ElemTerbe(I); Kepre;
lbKesz.Caption:= 'Vége';
End;
lbKesz.Visible:= True;
edStop.Text:= TimeToStr(GetTime);
end;
procedure TfmFKK.edMaxChange(Sender: TObject);
Var Kod: Integer;
begin
Val(edMax.Text,Max,Kod);
end;
procedure TfmFKK.edIMaxChange(Sender: TObject);
Var Kod: Integer;
begin
Val(edIMax.Text,IMax,Kod);
end;
end.