Bűvös négyzet készítése Genetikus algoritmussal

Bűvös négyzet alatt olyan négyzetes számtáblázatot értünk, amelynek soraiban, oszlopaiban és átlóiban elhelyezkedő számok összege mindig ugyanaz. Az átlók mellett néha az átlókkal párhuzamosan elhelyezkedő (mellékátlókban lévő) számok összegét is be szokták venni ebbe a kritériumba, néha csak bizonyos számokat, például csak prímeket, néha tetszőleges számokat írhatunk a négyzetekbe.

Az alap bűvös négyzetekben mindig 1-től n²-ig szerepelnek a számok. Ebben a fejezetben ilyen bűvös négyzetek generálásáról lesz szó. A generálást genetikus algoritmus segítségével fogjuk megoldani.

Egyedeknek az 1-től n²-ig terjedő számok egy permutációját fogjuk tekinteni. Egy populációban maximum 40 egyedet fogunk szerepeltetni, míg a generációk maximális számát 10000-ben határozzuk meg. Ezek értékeket természetesen az algoritmus beindítása előtt módosíthatók.

Az egyedek minősítése (fitness értéke, ami most inkább bad points-nak lenne mondható) a következő: minden n-re a program az egyedek generálásakor megállapítja a bűvös szám értékét, azaz kiszámolja 1-től n²-ig a számok összegét és osztja n-el. Ennek kellene lenni minden összegnek a sorokban, oszlopokban és a két átlóban. A fitness érték úgy adódik, hogy minden sorban és oszlopban, valamint a két átlóban meghatározzuk a tényleges összegeket, vesszük mindegyiknek az eltérését a szükséges értéktől és összeadjuk az így kapott 2*n+2 darab számot. Ez egy véletlen feltöltés esetén nagyobb, mint 0. Minél kisebb ez az összeg annál jobbnak tartunk egy egyedet. Ha az összeg 0, akkor a táblázat egy bűvös négyzet.

A genetikus algoritmus lépései a következők:

A 0. generáció előállítása, mely 40 db permutációja az 1-n² számoknak.

Szelekciónál két jó minősítésű (a fitness értékek átlagánál kisebb) egyedet választunk a keresztezéshez szülőként. Az egyik szülő mindig olyan, hogy nála jobb tulajdonságú nincs a populációban.

Keresztezésnél a következőre kell figyelnünk: az egyedek önmagukban hordozzák azt a megkövetelt tulajdonságot (fenotípusát), hogy csupa különböző számból állnak. Az egyszerű egy, vagy többpontos keresztezéseknél könnyen adódna olyan egyed, mely ezt a tulajdonságát elveszítené, életképtelenné lenne. Az életképtelen egyedek kiszűrése külön problémát és az algoritmus szempontjából fölösleges lépések sokaságát jelentené. Csak olyan keresztezési módszert engedhetünk meg, amelyek a permutációkon újra permutációkat (csupa különböző géneket) állít elő az egyes egyedeken belül. Három ilyen keresztezési módszer közül választhatunk a generálás előtt:

- Partially Matched Crossover (PMX), mely egy két vágási pontos keresztezés, melynél a vágási pontok közötti gének helyet cserélnek, majd a kialakított génpárok segítségével a gének kicserélésre kerülnek.

- Order Crossover (OX), mely szintén egy kétpontos keresztezés, ahol a szülőkből a gének a ciklikus sorrendjük megtartásával kerülnek át az utódokba.

- Cycle Crossover (CX), mely vágási pont nélküli keresztezés, melyben a gének egymásba kapcsolásával egy ciklust hozunk létre. A ciklusban szereplő egyedek az utódokban ugyanott szerepelnek, míg a ciklusból kimaradt gének kicserélődnek. (Itt az is előfordulhat, hogy a gének teljes láncot alkotnak, vagy csak egyelemű láncot, és ekkor az utódok génkészlete a szülőkkel megegyezik.)

Mutációnál az alapértelmezett értéket 30-nak állítottam be, amely 0,3 valószínűségű változtatást jelent a populáció minden rossz egyedének minden génjére. A jó egyedek génjeninél egy 5 értékű rátát alkalmaz az algoritmus, valamint a legjobb egyed génjeit nem változtatja.

Mind keresztezésnél, mind a mutációnál csak olyan egyedek kerülhetnek az új populációba, melyek lényegesen nem rosszabb tulajdonságúak, mint elődeik. Nevezetesen a megengedett romlás 5%-nyi. A sikertelen egyedgenerálást ellenére a program új generációként kezeli az ebben az esetben változatlanul hagyott populációt is (ha nem így lenne akkor nem vennénk észre a beragadást egy állapotba, külön figyelni kellene erre is egy változóval, melyet ki kellene íratni).

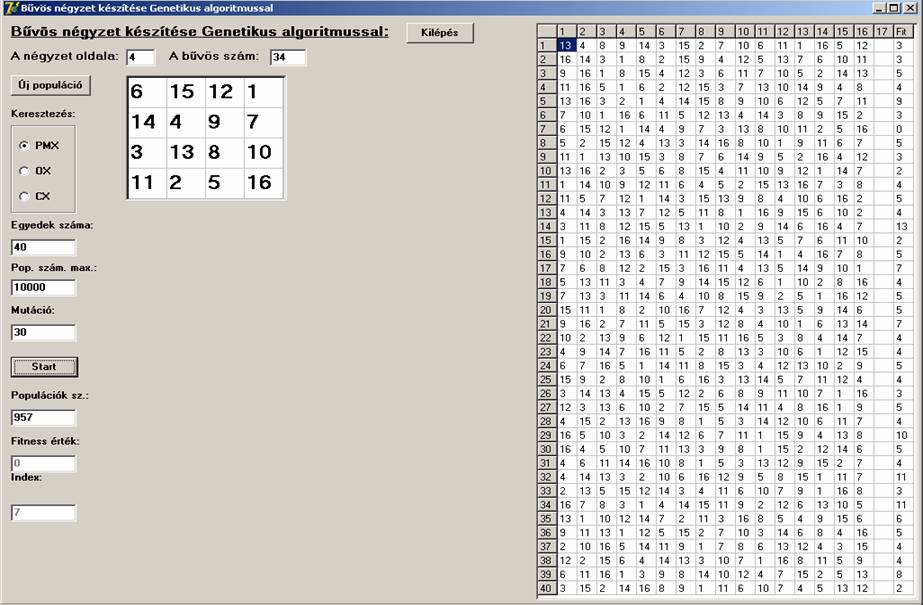
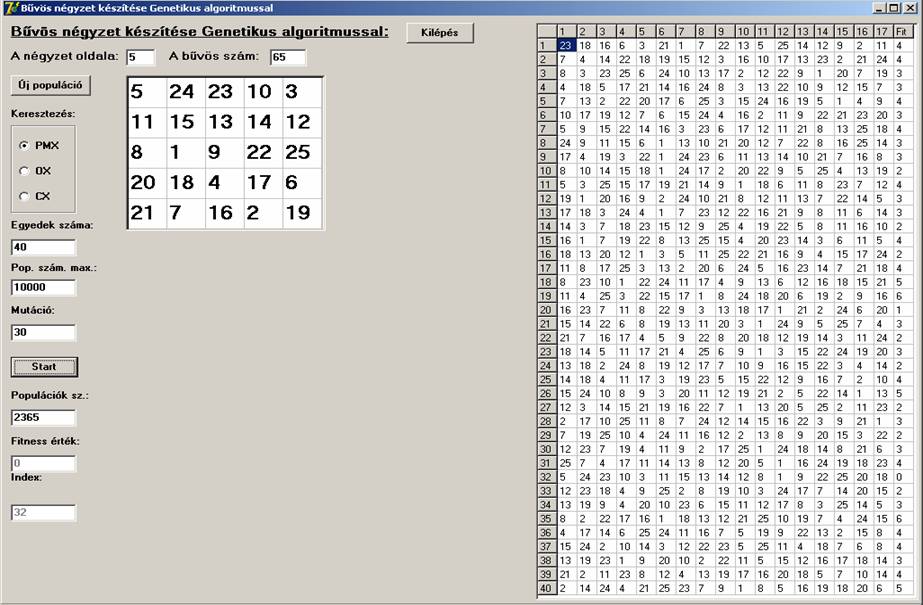
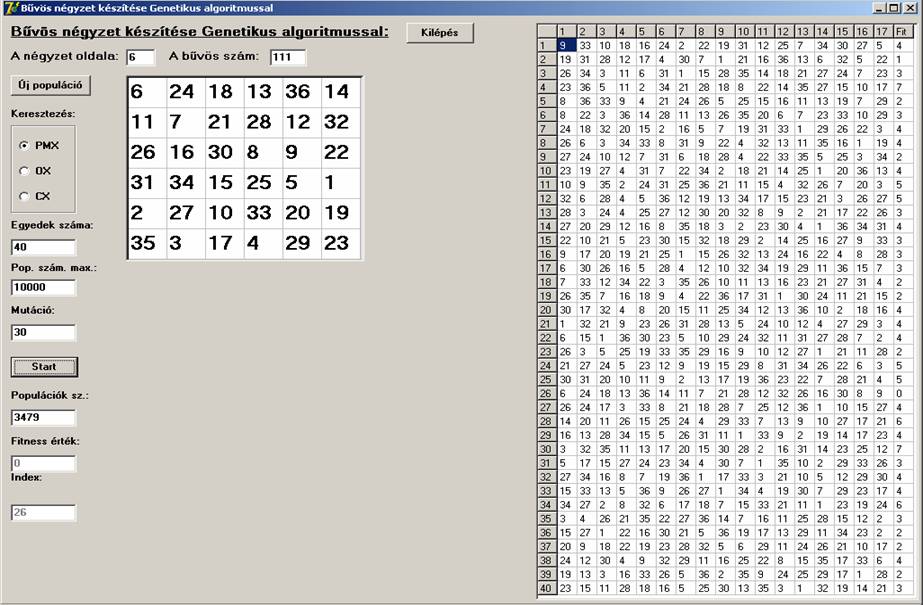
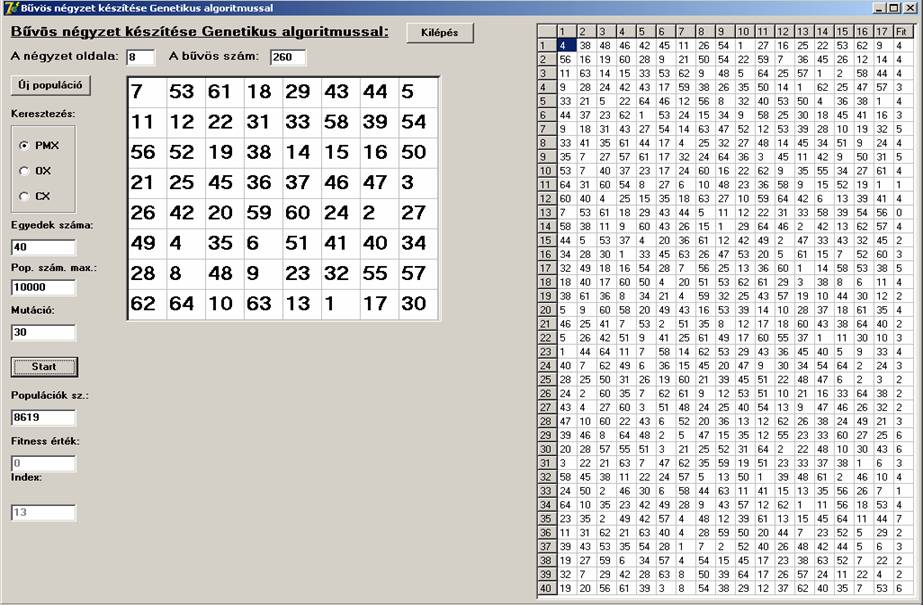
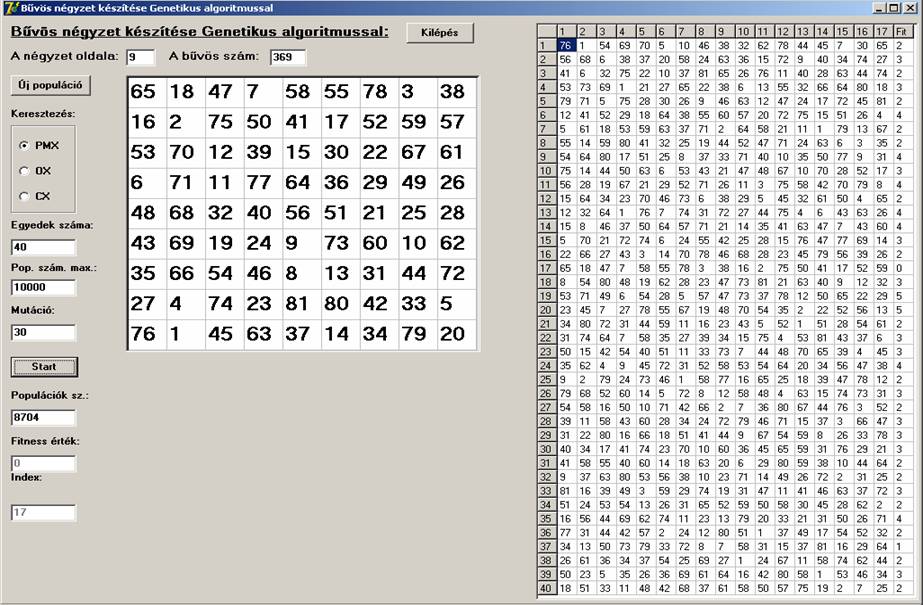
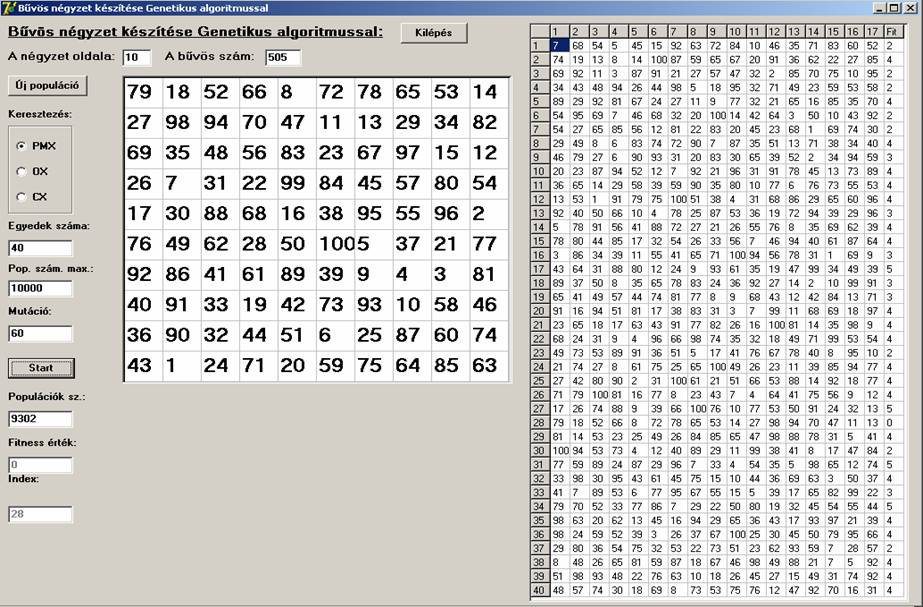
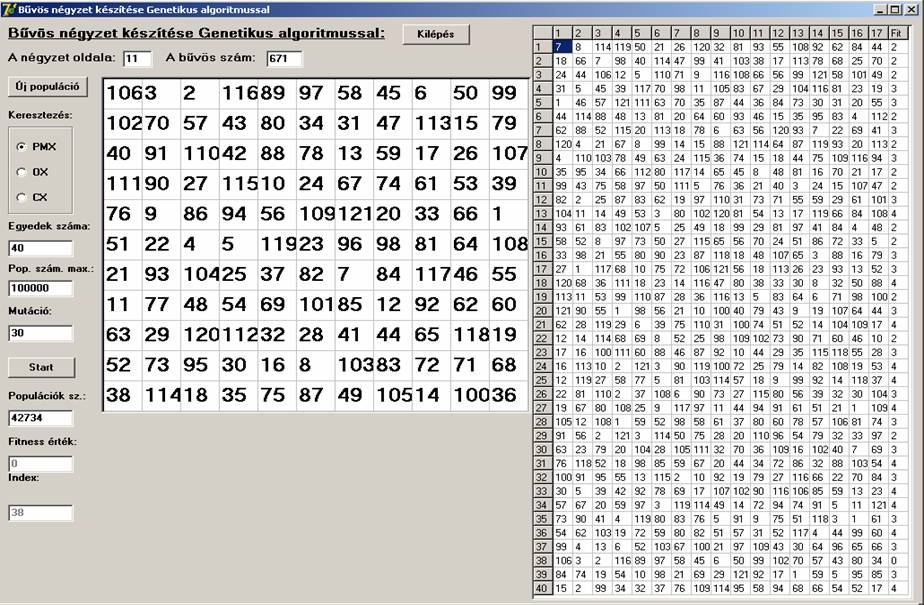
A továbbiakban n=3-tól n=11-ig egy-egy screenshot-on megtekinthetjük a generált bűvös nézeteket. A 40 egyed fitness értékeit és a génjeit is megjeleníti a program, de génekből csak maximum az első 17-et.

A program listája:

unit UGenBuv;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes, 

Graphics, Controls, Forms, Dialogs, StdCtrls, Grids, ExtCtrls;

Const Max=20;
EgyedSzM=100;
      GAL=3;

type
TfmGenBuv = class(TForm)
lbGenBuv: TLabel;
btKilepes: TButton;
lbNegyzOld: TLabel;
edNOld: TEdit;
btStart: TButton;
sgGenBuv: TStringGrid;
sgEgyed: TStringGrid;
btUjPop: TButton;
edPopSz: TEdit;
edKesz: TEdit;
lbPopSz: TLabel;
lbFitness: TLabel;
lbKereszt: TLabel;
rgKereszt: TRadioGroup;
lbBuvosSz: TLabel;
edBuvosSz: TEdit;
lbIndex: TLabel;
edIndex: TEdit;
lbPopSzM: TLabel;
edPopSzM: TEdit;
lbEgyedSz: TLabel;
edEgyedSz: TEdit;
edMutSz: TEdit;
lbMutSz: TLabel;
Procedure PopInit;
Procedure Josaga(E: Word);
Procedure Vizsgal;
Procedure PopKepre;
Procedure Tablara(E: Word);
Procedure Keresztez;
Procedure Mutacio;
procedure btKilepesClick(Sender: TObject);
procedure btStartClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure edNOldChange(Sender: TObject);
procedure btUjPopClick(Sender: TObject);
procedure edPopSzMChange(Sender: TObject);
procedure edEgyedSzChange(Sender: TObject);
procedure edMutSzChange(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

TSzam=Record
    NN: Array[1..Max*Max] Of Word;
End;

TEgyed=Record
    ENN: TSzam;
    EOK: Word;
EJo: Boolean;
End;
var
fmGenBuv: TfmGenBuv;
EgyedT: Array[0..EgyedSzM] Of TEgyed;
Josag: Real;
  Uj1, Uj2: TEgyed;
EgyedSz, NOld, Tablan, JokSz, Ker1, Ker2, Kozep, OsszJo: Word;
  IR1, IR2, IJ1, IJ2, OKMin, IMin, OldMin, MutSz: Word;
PopSz, PopSzM: LongInt;

implementation

{$R *.dfm}

procedure TfmGenBuv.btKilepesClick(Sender: TObject);
begin
Close;
end;

procedure TfmGenBuv.FormCreate(Sender: TObject);
Var I: Integer;
begin
Randomize;
EgyedSz:= 40; Mutsz:= 30; PopSz:= 1; PopSzM:= 10000;
rgKereszt.ItemIndex:= 0;
btStart.Enabled:= False;

With sgEgyed Do
Begin
RowCount:= EgyedSz+1;
For I:= 1 To ColCount-2 Do Cells[I,0]:= IntToStr(I);
For I:= 1 To RowCount-1 Do Cells[0,I]:= IntToStr(I);
Cells[ColCount-1,0]:= 'Fit';
End;

end;

procedure TfmGenBuv.edPopSzMChange(Sender: TObject);
Var Kod: Integer;
begin
Val(edPopSzM.Text,PopSzM,Kod);
end;

procedure TfmGenBuv.edEgyedSzChange(Sender: TObject);
Var Kod: Integer;
begin
Val(edEgyedSz.Text,EgyedSz,Kod);
end;

procedure TfmGenBuv.edMutSzChange(Sender: TObject);
Var Kod: Integer;
begin
Val(edMutSz.Text,MutSz,Kod);
end;

procedure TfmGenBuv.edNOldChange(Sender: TObject);
Var Kod: Integer;
begin
Val(edNOld.Text,NOld,Kod); If NOld<3 Then NOld:= 3;
edNOld.Text:= IntToStr(NOld);
btStart.Enabled:= False;
end;

Procedure TfmGenBuv.PopInit;
Var I, J, K, L, P: Word;
    T: TSzam;
Begin
For I:= 1 To Max*Max Do T.NN[I]:= I;
For K:= 1 To EgyedSz Do With EgyedT[K] Do
Begin
For L:= 1 To Max*Max*Max Do
Begin
Repeat
I:= Random(NOld*NOld)+1;
        J:= Random(NOld*NOld)+1;
Until I<>J;
      P:= T.NN[I]; T.NN[I]:= T.NN[J]; T.NN[J]:= P;
End;
    ENN:= T;
    EOK:= 0;
EJo:= False;
End;
End;

Procedure TfmGenBuv.Josaga(E: Word);
Var I, J, N, S: Word;
    V: Array[1..Max,1..Max] Of Word;
Begin
With EgyedT[E] Do
Begin
For I:= 1 To NOld*NOld Do V[(I-1) Mod NOld+1,(I-1) Div NOld+1]:= ENN.NN[I];
    S:= 0;
For I:= 1 To NOld Do
Begin
      N:= 0; For J:= 1 To NOld Do Inc(N,V[I,J]); Inc(S,Abs(N-Kozep));
      N:= 0; For J:= 1 To NOld Do Inc(N,V[J,I]); Inc(S,Abs(N-Kozep));
End;
N:= 0; For J:= 1 To NOld Do Inc(N,V[J,J]); Inc(S,Abs(N-Kozep));
    N:= 0; For J:= 1 To NOld Do Inc(N,V[J,NOld-J+1]); Inc(S,Abs(N-Kozep));
    EOK:= S;
End;
End;

Procedure TfmGenBuv.Vizsgal;
Var I: Word;
Begin
OsszJo:= 0; OKMin:= 65000; IMin:= 1;
For I:= 1 To EgyedSz Do With EgyedT[I] Do
Begin Inc(OsszJo,EOK); If EOK<OKMin Then Begin OKMin:= EOK; IMin:= I End End;
Josag:= OsszJo/EgyedSz;
For I:= 1 To EgyedSz Do With EgyedT[I] Do If EOK<Josag Then
EJo:= True Else EJo:= False;
End;

Procedure TfmGenBuv.PopKepre;
Var I, J: Word;
Begin
With sgEgyed Do
Begin
For I:= 1 To ColCount-1 Do For J:= 1 To RowCount-1 Do Cells[I,J]:= '';
For J:= 1 To EgyedSz Do With EgyedT[J] Do For I:= 1 To NOld*NOld Do
Begin
Cells[I,J]:= IntToStr(ENN.NN[I]);
Cells[ColCount-1,J]:= IntToStr(EOK);
End;
End;
End;

Procedure TfmGenBuv.Tablara(E: Word);
Var I: Word;
Begin
With sgGenBuv Do For I:= 1 To NOld*NOld Do
Cells[(I-1) Mod NOld+1,(I-1) Div NOld+1]:= IntToStr(EgyedT[E].ENN.NN[I]);
End;

Procedure TfmGenBuv.Keresztez;
Var I, J, V, R, A, B, C, P, T, U: Word;
    P1, P2: TSzam;
    Van: Boolean;
Begin
  Inc(PopSz);

V:= Random(EgyedSz)+1; R:= 0; IR1:= 0;
For I:= V+1 To EgyedSz Do With EgyedT[I] Do
If Not EJo And (EOK>R) Then Begin R:= EOK; IR1:= I End;
For I:= 1 To V  Do With EgyedT[I] Do
If Not EJo And (EOK>R) Then Begin R:= EOK; IR1:= I End;

  V:= Random(EgyedSz)+1; R:= 0; IR2:= 0;
For I:= V+1 To EgyedSz Do With EgyedT[I] Do If I<>IR1 Then
If Not EJo And (EOK>R)Then Begin R:= EOK; IR2:= I End;
For I:= 1 To V  Do With EgyedT[I] Do If I<>IR1 Then
If Not EJo And (EOK>R) Then Begin R:= EOK; IR2:= I End;

  V:= Random(EgyedSz)+1; R:= 65000; IJ1:= 0;
For I:= V+1 To EgyedSz Do With EgyedT[I] Do
If EJo And (EOK<R) Then Begin R:= EOK; IJ1:= I End;
For I:= 1 To V  Do With EgyedT[I] Do
If EJo And (EOK<R) Then Begin R:= EOK; IJ1:= I End;

  V:= Random(EgyedSz)+1; IJ2:= 0;
For I:= V+1 To EgyedSz Do With EgyedT[I] Do If I<>IJ1 Then
If EJo Then IJ2:= I;
For I:= 1 To V  Do With EgyedT[I] Do If I<>IJ1 Then
If EJo Then IJ2:= I;

//keresztezés -> Uj1, Uj2: TEgyed
If IJ1*IJ2*IR1*IR2<>0 Then
Begin
    Uj1:= EgyedT[IJ1];
    Uj2:= EgyedT[IJ2];
Case rgKereszt.ItemIndex Of
0: Begin //PMX (Partially Matched Crossover)
           A:= 0; B:= 0;
For I:= Ker1+1 To Ker2 Do
Begin
For J:= 1 To NOld*NOld Do
If Uj1.ENN.NN[J]=Uj2.ENN.NN[I] Then A:= J;
For J:= 1 To NOld*NOld Do
If Uj2.ENN.NN[J]=Uj1.ENN.NN[I] Then B:= J;
             P:= Uj1.ENN.NN[I];
             Uj1.ENN.NN[I]:= Uj2.ENN.NN[I];
             Uj2.ENN.NN[I]:= P;
             P:= Uj1.ENN.NN[A];
             Uj1.ENN.NN[A]:= Uj2.ENN.NN[B];
             Uj2.ENN.NN[B]:= P;
End;
End;
1: Begin //OX (Order Crossover)
           P1:= Uj1.ENN;
           P2:= Uj2.ENN;

For I:= Ker1+1 To Ker2 Do For J:= 1 To NOld*NOld Do
If Uj2.ENN.NN[J]=P1.NN[I] Then Uj2.ENN.NN[J]:= 0;
For I:= Ker1+1 To Ker2 Do For J:= 1 To NOld*NOld Do
If Uj1.ENN.NN[J]=P2.NN[I] Then Uj1.ENN.NN[J]:= 0;

           A:= 0; B:= 0;
For I:= Ker1+1 To NOld*NOld Do
Begin
If Uj1.ENN.NN[I]<>0 Then
Begin
               Inc(A); If A=Ker1+1 Then A:= Ker2+1; P1.NN[A]:= Uj1.ENN.NN[I];
End;
If Uj2.ENN.NN[I]<>0 Then
Begin
               Inc(B); If B=Ker1+1 Then B:= Ker2+1; P2.NN[B]:= Uj2.ENN.NN[I];
End;
End;

For I:= 1 To Ker1 Do
Begin
If Uj1.ENN.NN[I]<>0 Then
Begin
               Inc(A); If A=Ker1+1 Then A:= Ker2+1; P1.NN[A]:= Uj1.ENN.NN[I];
End;
If Uj2.ENN.NN[I]<>0 Then
Begin
               Inc(B); If B=Ker1+1 Then B:= Ker2+1; P2.NN[B]:= Uj2.ENN.NN[I];
End;
End;

With Uj1.ENN Do
Begin
For I:= 1 To Ker1 Do NN[I]:= P1.NN[I];
For I:= Ker1+1 To Ker2 Do NN[I]:= P2.NN[I];
For I:= Ker2+1 To NOld*NOld Do NN[I]:= P1.NN[I];
End;

With Uj2.ENN Do
Begin
For I:= 1 To Ker1 Do NN[I]:= P2.NN[I];
For I:= Ker1+1 To Ker2 Do NN[I]:= P1.NN[I];
For I:= Ker2+1 To NOld*NOld Do NN[I]:= P2.NN[I];
End;

End;
      2: Begin //CX (Cycle Crossover)
For I:= 1 To NOld*NOld Do Begin P1.NN[I]:= 0; P2.NN[I]:= 0 End;
For I:= 1 To NOld*NOld Do If Uj1.ENN.NN[I]=Uj2.ENN.NN[I] Then
Begin P1.NN[I]:= Uj1.ENN.NN[I]; P2.NN[I]:= Uj2.ENN.NN[I] End;
           A:= 1;
While P1.NN[A]<>0 Do Inc(A); B:= A;
Repeat
             P1.NN[A]:= Uj1.ENN.NN[A];
             P2.NN[A]:= Uj2.ENN.NN[A];
             C:= 0; For J:= 1 To NOld*NOld Do
If Uj1.ENN.NN[J]=P2.NN[A] Then C:= J; A:= C;
Until A=B;
For I:= 1 To NOld*NOld Do
Begin
If P1.NN[I]=0 Then P1.NN[I]:= Uj2.ENN.NN[I];
If P2.NN[I]=0 Then P2.NN[I]:= Uj1.ENN.NN[I];
End;
           Uj1.ENN:= P1;
           Uj2.ENN:= P2;
End;
End;
EgyedT[0]:= Uj1; Josaga(0); T:= EgyedT[0].EOK;
EgyedT[0]:= Uj2; Josaga(0); U:= EgyedT[0].EOK;

If T+U<=1.05*(EgyedT[IR1].EOK+EgyedT[IR2].EOK) Then
Begin
EgyedT[IR1]:= Uj1; Josaga(IR1);
EgyedT[IR2]:= Uj2; Josaga(IR2);
End;
End;
End;

Procedure TfmGenBuv.Mutacio;
Var I, J, K, L, P, U: Word;
    T: TSzam;
Begin
  Inc(PopSz);
For L:= 1 To EgyedSz Do With EgyedT[L] Do
If L<>IMin Then For K:= 1 To NOld Do
If Not EJo And (Random(100)<MutSz) Or EJo And (Random(100)<MutSz/5) Then
Begin
    U:= EOK;
    T:= ENN;
Repeat
      I:= Random(NOld*NOld)+1;
      J:= Random(NOld*NOld)+1;
Until I<>J;
    P:= T.NN[I]; T.NN[I]:= T.NN[J]; T.NN[J]:= P;
EgyedT[0].ENN:= T;
Josaga(0);
If EgyedT[0].EOK<=1.05*U Then ENN:= T;
End;
End;

procedure TfmGenBuv.btStartClick(Sender: TObject);
Var I: Word;
begin
rgKereszt.Enabled:= False;
btUjPop.Enabled:= False;
OKMin:= 65000; IMin:= 0; PopSz:= 1;
Repeat
OldMin:= OKMin; edPopSz.Text:= IntToStr(PopSz); edPopSz.Repaint;
If IJ1*IJ2*IR1*IR2<>0 Then Keresztez Else
Begin Mutacio; For I:= 1 To EgyedSz Do Josaga(I) End;
Vizsgal; PopKepre; sgEgyed.Repaint;
If OKMin<OldMin Then
Begin
edKesz.Text:= IntToStr(OKMin); edKesz.Repaint;
edIndex.Text:= IntToStr(IMin); edIndex.Repaint;
Tablara(IMin); sgGenBuv.Repaint;
End;
Until (OKMin=0) Or (PopSz>PopSzM);

Tablara(IMin);
rgKereszt.Enabled:= True;
btUjPop.Enabled:= True;

end;

procedure TfmGenBuv.btUjPopClick(Sender: TObject);
Var I, J: Word;
Kod: Integer;
begin
Val(edNOld.Text,NOld,Kod);
Kozep:= (NOld*NOld*(NOld*NOld+1) Div 2) Div NOld;
edBuvosSz.Text:= IntToStr(Kozep);
  Ker1:= NOld*NOld Div 3; Ker2:= 2*NOld*NOld Div 3;
With sgGenBuv Do
Begin
DefaultColWidth:= 42;
DefaultRowHeight:= 36;
Width:= 43*NOld+7;
Height:= 37*NOld+5;
ColCount:= NOld+2;
RowCount:= NOld+2;
ColWidths[0]:= 0;
RowHeights[0]:= 0;
ColWidths[ColCount-1]:= 0;
RowHeights[RowCount-1]:= 0;
    Col:= ColCount-1;
Row:= RowCount-1;
For I:= 0 To ColCount-1 Do For J:= 1 To RowCount-1 Do Cells[I,J]:= '';
Visible:= True;
End;
PopInit;
For I:= 1 To EgyedSz Do Josaga(I);
Vizsgal;
PopKepre;
btStart.Enabled:= True;
end;

end.