Palindromszámok
Egy karaktersort Palindromnak nevezünk, ha elölről és a végéről olvasva is ugyanazon karaktersorozatot kapjuk. Közismert, Palindromnak nevezett magyar mondatok a következők:
- Géza kék az ég
- Indul a pap aludni
- Kis Elek elesik, stb.
Ezek a példák csak kiejtés szerinti Palindromok, mert szigorú értelemben nem azok, a figyelembe nem vett szóközök, illetve a kis- és nagy betűk különbözősége miatt.
Egy számot Palindromszámnak nevezünk, ha valamelyik számrendszerben számjegyei szigorú értelemben véve Palindrom karaktersort alkotnak. Számos Web helyen utánanézhetünk például a 10-es és számrendszerekben Palindrom számoknak, de nem 10-es számrendszerbeli Palindrom számokra is számos példát találunk. Megadják számukat és képzési eljárásukat.
Tennék egy kis látszólagos kitérőt. Amikor az információ egységéről és méréséről tanulunk informatika órán, fel szoktam tenni azt a kérdést, hogy hány bit információhoz jutunk, ha valakinek megtudjuk a születésnapját. A megoldás igen egyszerű. Mivel 366-féle lehetőségből tudjuk meg azt, hogy melyik a születésnap, ezért a 365-öt (a szabály szerint 366-1-et) felírjuk kettes számrendszerben, ahány jegyű kettes számrendszerbeli számot kapunk, annyi bit-egész információmennyiséghez jutottunk. (Az információmennyiség meghatározási szabálya szerint, a lehetséges eseteknek egyformán valószínűnek kell lenni, ami itt nem teljesül, hiszen február 29-e valószínűsége a többinek a negyede. De, mivel az információt csak egész számként – és nem valósként – kapjuk, így ez az eredményen – a bitek számában – nem jelent különbséget, hiszen a 365 messze van 2 bármelyik hatványától, tehát csak annyi a különbség, hogy az utolsó bit 0, vagy 1.) Az átírást osztással hajtjuk végre:
365 : 2 = 182, maradék 1.
182 : 2 = 91, maradék 0.
91 : 2 = 45, maradék 1.
45 : 2 = 22, maradék 1.
22 : 2 = 11, maradék 0.
11 : 2 = 5, maradék 1.
5 : 2 = 2, maradék 1.
2 : 2 = 1, maradék 0.
1 : 2 = 0, maradék 1.
A szabály szerint a maradékok fordított sorrendben (utolsó maradék az első jegy, az első pedig az utolsó) adják a kettes számrendszerbeli alakot. Történt aztán, hogy az egyik tanítvány elfelejtette ez utóbbi szabályrészt, azaz a maradékokat a létrejöttük sorrendjében írta fel. Speciálisan az eredmény ugyanaz, mint a fordított sorrend, merthogy ez a szám Palindrom. Ilyenkor fel szoktam tenni a diákoknak azt a kérdést, hogy vajon mely számok kettes számrendszerbeli alakja Palindrom. Nem volt még diák, aki azzal fordult volna hozzám, hogy foglalkozott a problémával, esetleg segítséget kért volna.
Így aztán magam kezdtem ebben a témában vizsgálódni. Sőt még tovább is léptem. Arra gondoltam, hogy az alapfeladat igen egyszerű, bonyolítsunk rajta egy kicsit. Így a jelen lapon elsőként arra a kérdésre keresem a választ, hogy melyek azok a számok, amelyek 10-es és 2-es számrendszerben is Palindromok. Írtam egy programot az ilyen számok megkeresésére. A programban megadhatjuk, hogy mely számtól induljon a keresés. A program a 0 kivételével csak páratlan számok között keres, hiszen egy kettes számrendszerbeli szám biztosan 1-el kezdődik, és mivel Palindrom, 1-re is kell végződnie, azaz a szám biztosan páratlan. Start után a minél gyorsabb futás érdekében csak minden tízmilliomodik számnál frissül a képernyő. A program kiírja az utolsónak megtalált számot és a megtalálási időpontját is. A kapott listát egy Palind.csv állományba ki is menthetjük, sőt a következő futtatás idején be is tölthetjük, azzal a számmal együtt, ameddig a program a vizsgálat során már eljutott. Ez utóbbira a hosszú futási idő miatt van szükség, így több menetben eljuthatunk nagyon nagy számokig.
A megfelelő tulajdonságú számok száma nem lehet túl nagy, hiszen – mint ahogy azt a futtatási kép is mutatja – 1000 milliárdig csak 39 ilyen szám van. A program futtatási képe a 1000 milliárdig tartó keresés végén – mely napokig tartott – a következő:
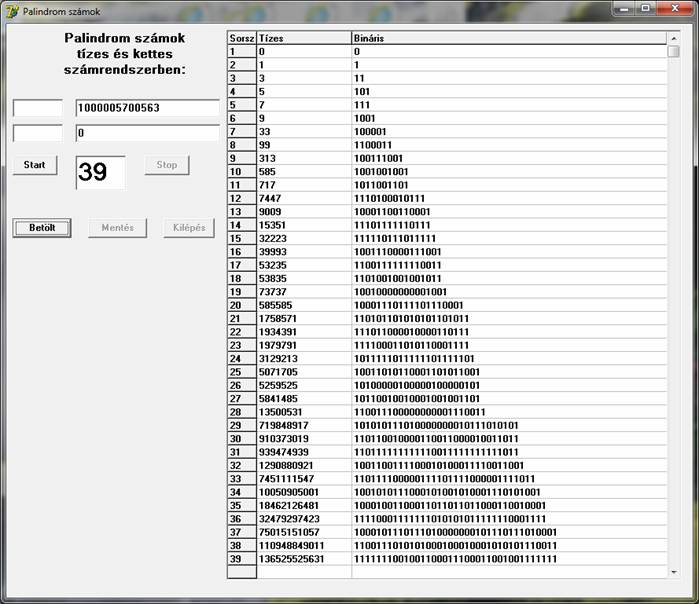
Ezek alapján szerintem elég logikus a következő kérdés: vajon hány ilyen szám létezik, ha ekkora értékig csak 39-et találtam. Vajon véges vagy végtelen az ilyen számoknak a száma? A választ egyelőre nem tudom. Ha valakinek van ötlete hozzá, szívesen megismerném.
A következő általánosítás abban az irányban történt, hogy mi a helyzet akkor, ha a 10-es mellett nem 2-es, hanem 3-as számrendszerben keresünk. Palindrom alakokat. Most csak 1 milliárdig kerestem. Íme a futási kép:
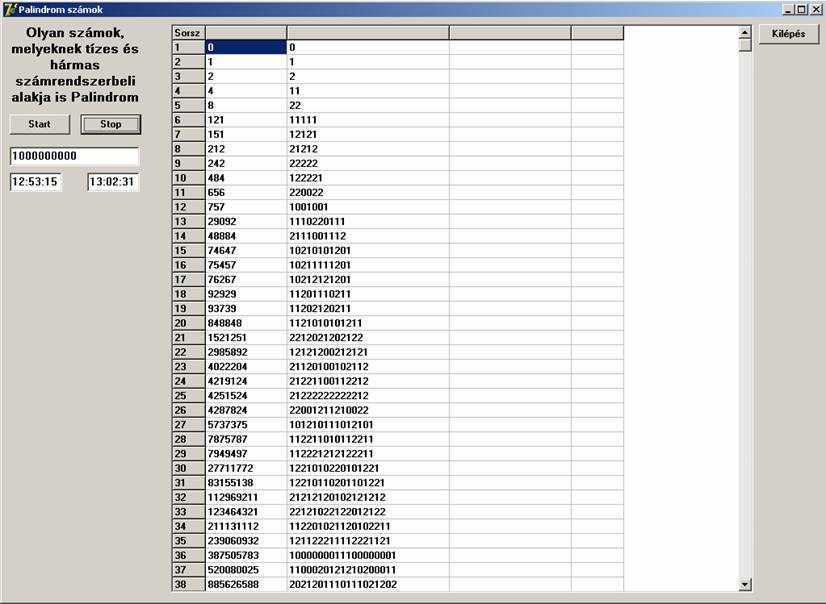
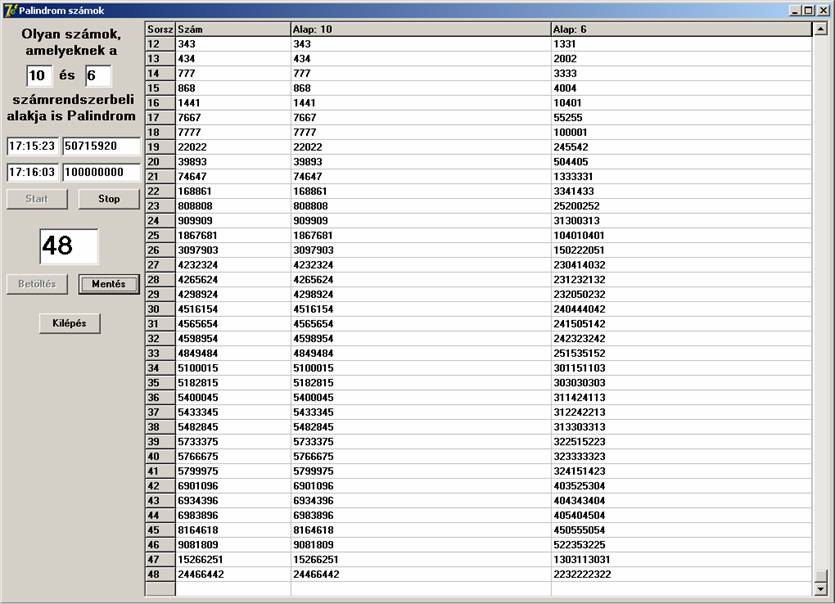
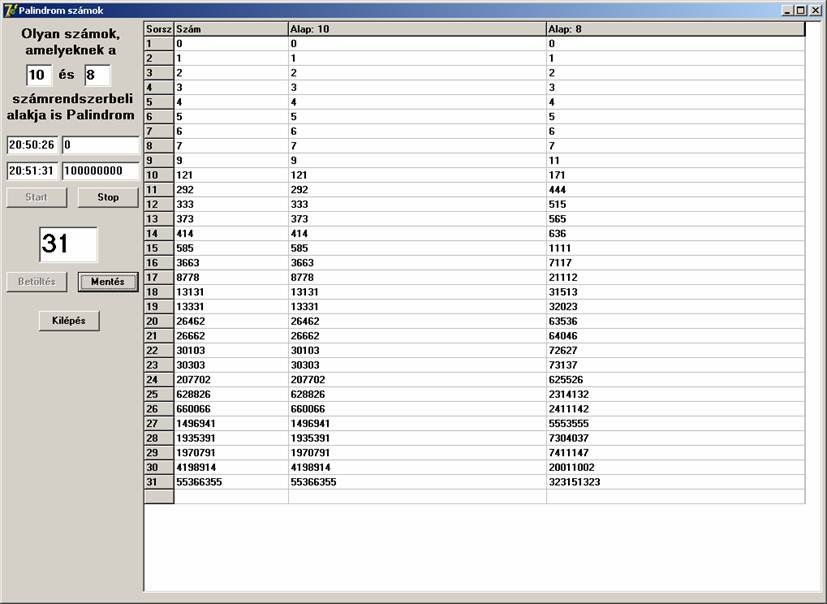
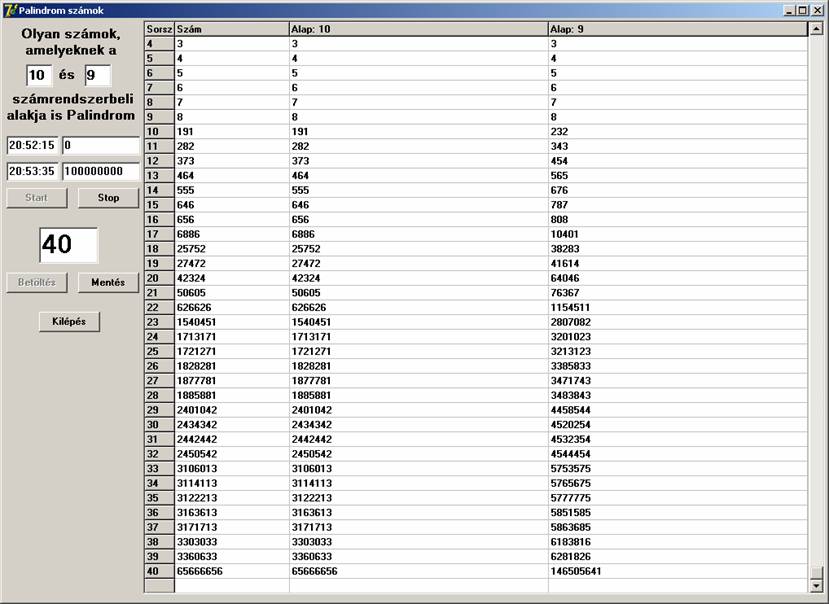
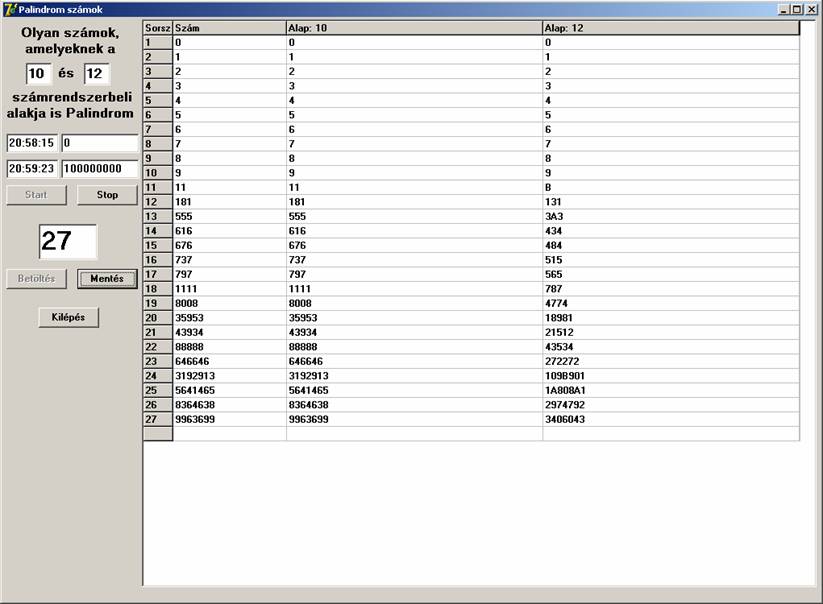
Ekkor úgy döntöttem, hogy általánosítom a program lehetőségeit. Lehessen inputon megadni azt a két alapot, amelyben keresünk. Az első alap mindig 10 volt, a másodikat 16-ig változtattam, valamint 100 millióig történt a keresés. A futási képek:
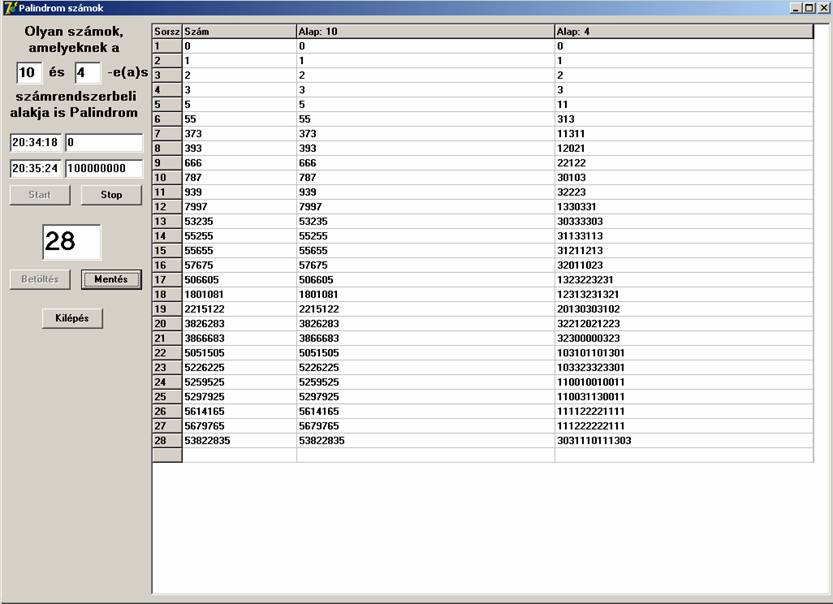




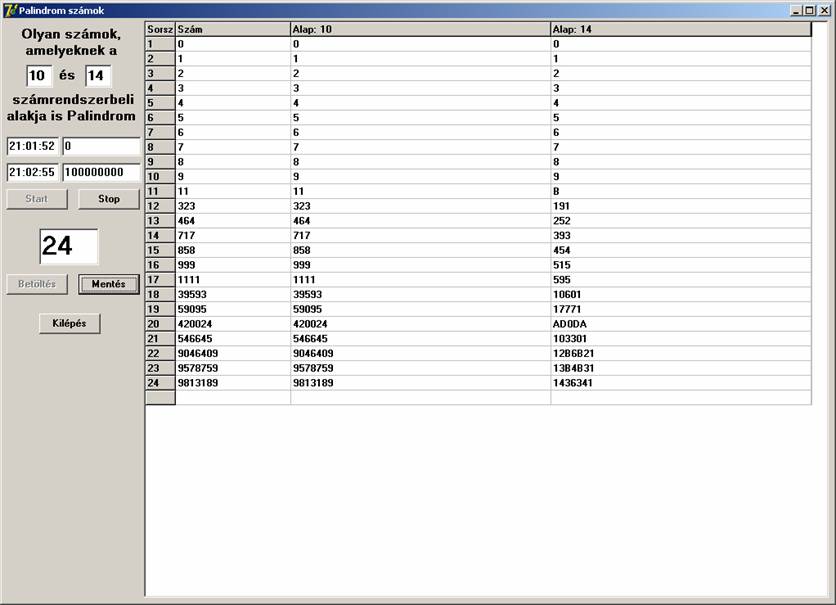
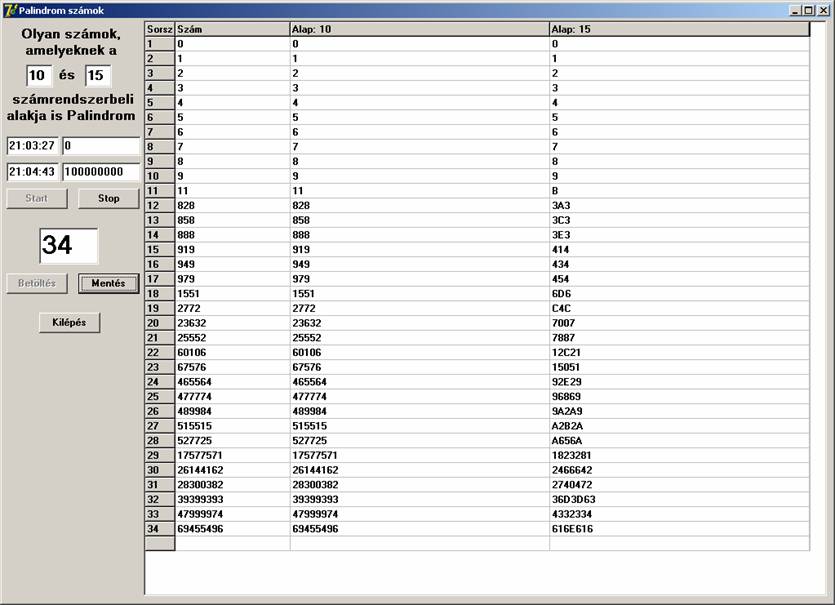
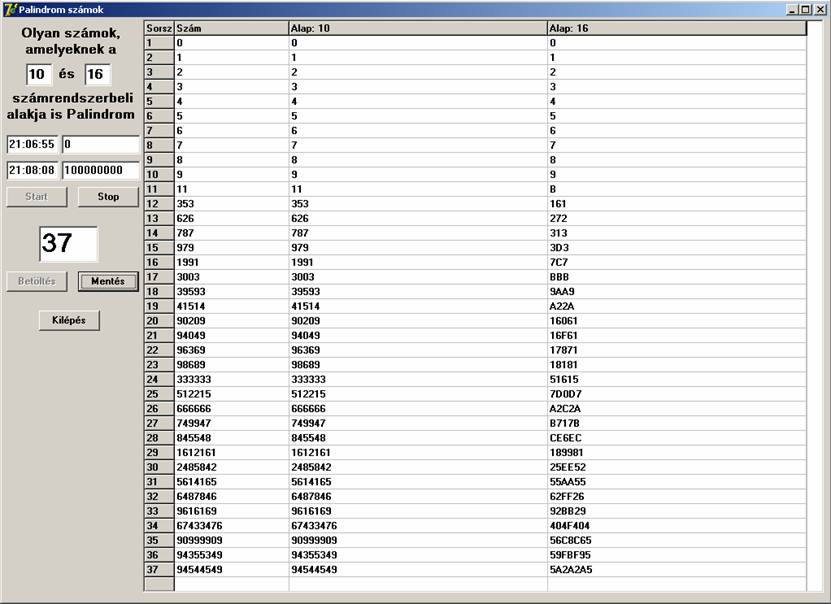
Összefoglalva:
10 – 2: 39 db 1 billióig.
10 – 3: 32 db 100 millióig.
10 – 4: 28 db ’’
10 – 5: 20 db ’’
10 – 6: 48 db ’’
10 – 7: 20 db ’’
10 – 8: 31 db ’’
10 – 9: 40 db ’’
10 – 11: 52 db ’’
10 – 12: 27 db ’’
10 – 13: 41 db ’’
10 – 14: 24 db ’’
10 – 15: 34 db ’’
10 – 16: 37 db ’’.
A következő lépés az volt, hogy elszakadtam a 10-es számrendszertől és két egymás utáni értéket választottam a két alapnak. (A futtatási határértékek azért kisebbek. mint fentebb, mert mindkét számrendszerbe át kell írni a 10-es alakról a számokat, így a vizsgálat időigényesebb.) A következő eredményeket kaptam:
2 – 3: 5 db 5 milliárdig.
3 – 4: 10 db 20 millióig.
4 – 5: 12 db 20 millióig
5 – 6: 17 db 10 millióig
6 – 7: 20 db 4 millióig
7 – 8: 27 db 10 millióig
8 – 9: 31 db 2 millióig
9 – 10: 32 db 2,5 millióig.
Ezek közül számomra a legérdekesebb az első. Kettes és hármas számrendszerben is Palindrom szám 5 milliárdig összesen 5 van, ráadásul ebből csak három a nem triviális, hiszen a 0 és az 1 bármilyen számrendszerben Palindrom. Nézzük ennek a futási képét:

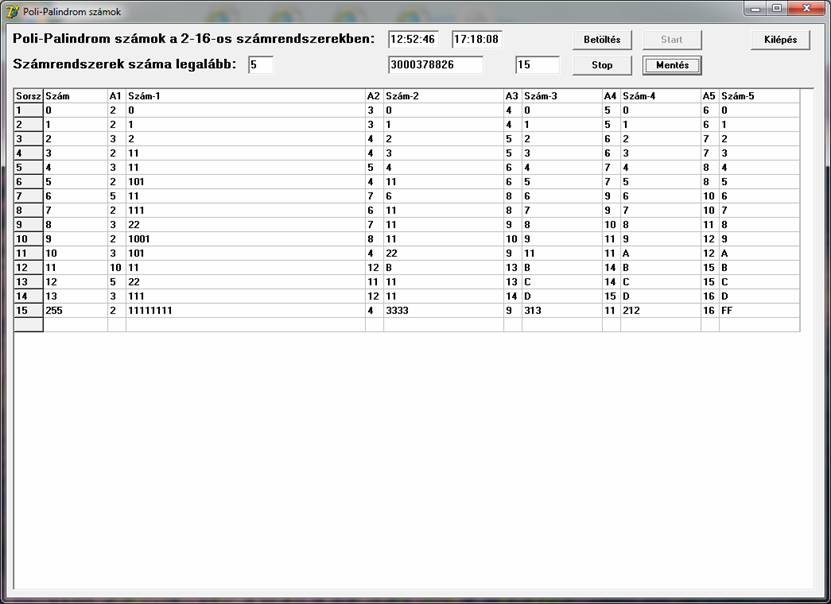
Nevezzem Poli-Palindrom számoknak azokat a számokat, amelyeknek kettőnél több számrendszerben is Palindrom az alakjuk. A táblázatok egyszerű összevetésével találtam egy olyan számot, ami négy számrendszerben is Palindrom: a tízes számrendszerbeli 373 négyesben 11311, nyolcasban 565, míg kilencesben 454 alakú. Nyilvánvaló volt a további vizsgálódási irány, keressünk minél több számrendszerben Palindrom számokat. Ennek érdekében tovább módosítottam a programot. Arra gondoltam, hogy a számrendszerek alapját 2-16 intervallumból választom. (Nincs semmi elvi akadálya, hogy az alap magasabb legyen, de úgy gondoltam számomra ezek az esetek is elég érdekesek lehetnek.) Az első futtatásoknál kiderült, hogy a triviális számok (0-16) kivételével kevés olyan szám van, ami 4-nél több számrendszerben is Palindrom és olyanból sincs túl sok, amely 4-ben is az. Lássunk egy ilyen futtatási képet, 1 milliárd értékig:
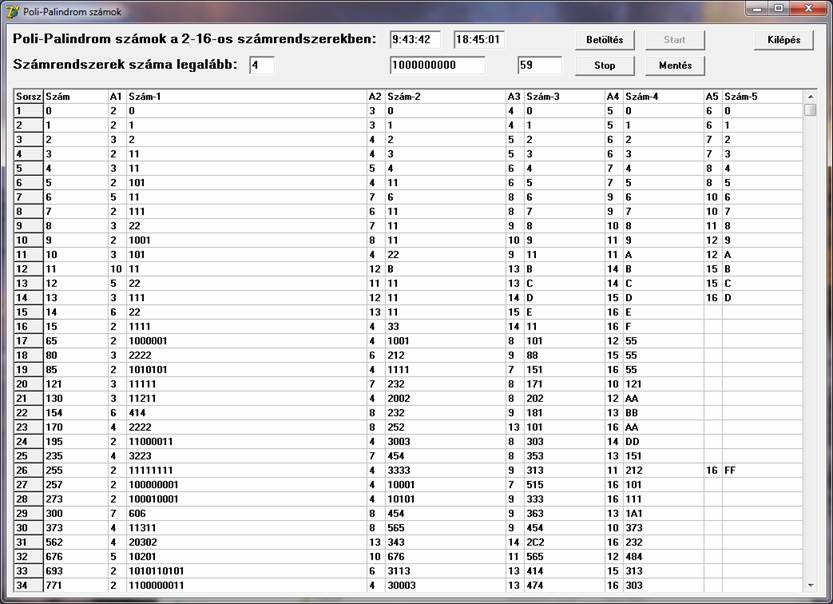
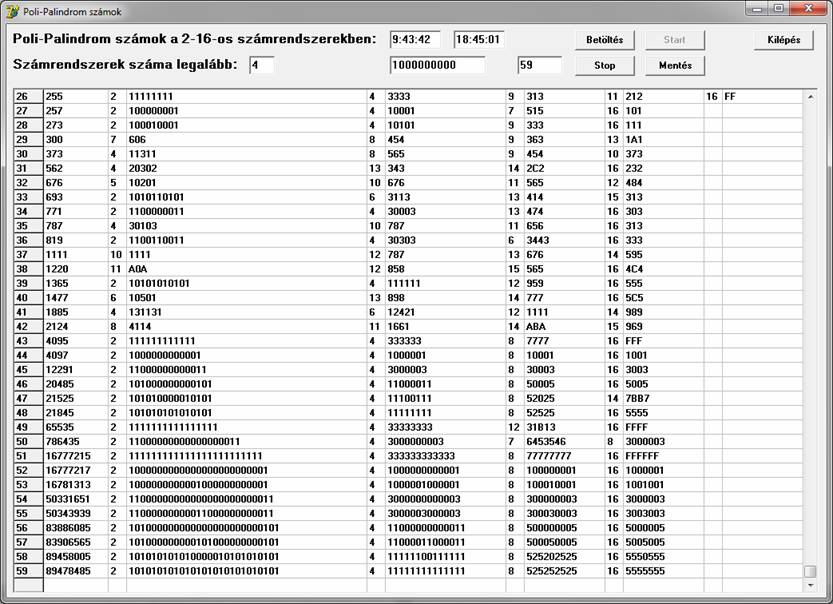
Csak maximálisan 5 számrendszerbeli alakot jelenítek meg. A lista elején 13-ig természetesen további Palindrom alakok lennének láthatók, de ezek mind eléggé triviális értékek, könnyen előállíthatók. 1 milliárdig összesen csak 59 olyan szám létezik, amelyik legalább 4 számrendszerben Palindrom alakú. A táblázat egyik érdekessége, hogy az utolsónak megtalált 9 szám mindegyike 2, 4, 8 és 16-os számrendszerekben Palindrom alakú.
A másik érdekesség, hogy a táblázatban található egy olyan nem triviális szám is, amely 5 számrendszerben is Palindrom. Ez a decimális 255. De több ilyet nem látunk. Ezért, csak ennek az esetnek a vizsgálatára újrafutattam a programot, ezúttal 3 milliárdig, de újabb ilyen tulajdonságú számot nem találtam: