Izogonális pont (5)

Egy geometriai szélsőérték feladat

Feladat: Adott a síkban n darab pont. Keresendő az a pont, amelyből az adott pontokba húzott szakaszok hosszának az összege – a sík bármely pontjára nézve – a lehető legkisebb.

Ebben a részben néhány konkrét esetre szintvonalakat fogunk rajzoltatni a programmal. Ha az (x, y) pont bejárja a síkot (független változók), akkor a távolságfüggvény egy kétváltozós függvény, melynek ábrázolása csak térben lehetséges (illetve síkban a teret érzékeltető ábrázolásmóddal, például axonometriával). A kétváltozós függvény tulajdonságairól, alakjáról fogalmat alkothatunk úgy is, ha az (x, y) síkkal párhuzamos metszeteit lerajzoljuk az (x, y) síkra. Ezeket szintvonalaknak nevezzük. Emlékeztetőül a függvényünk:

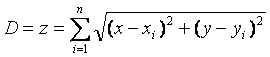
A szintvonalakat úgy kaphatjuk, hogy z-nek konkrét értéket adunk, majd az így kapott két-ismeretlenes egyenletet az y implicit függvényének tekintjük, és azt az (x, y) síkon ábrázoljuk.

Egy pont esetén ez nagyon egyszerű, könnyen felismerhető a kör egyenlete:

Két pont esetén is kitalálható, hogy mi az egyenlet. Ekkor ugyanis két ponttól vett távolságösszegnek kell állandónak lenni, ami nem más, mint az ellipszis. Már itt is gondok lehetnek az ábrázolással, hiszen a közismert egyenlet csak olyan helyzetű ellipszist ad meg, amelynek tengelyei koordinátatengelyekkel párhuzamos (kanonikus). Emlékeztetőül:

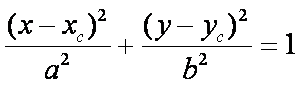
Ahol az a és b az ellipszis féltengelyei, (x_c, y_c) pedig a középpontja. Egy tetszőleges helyzetű ellipszis egyenlete pedig így néz ki:

Ax² + Bxy + Cy² + Dx+ Ex + F = 0

Ahol B²<4AC.

Több pontra a megoldás még bonyolultabb. Ehhez jó lenne, ha az y-t sikerülne kifejezni az összefüggésből. Az explicit alak előállítása már csak azért is akadályokba ütközik, mert négy vagy több négyzetgyököt és egy nem nulla tagot tartalmazó egyenletből a gyökök négyzetre emeléssel el sem tüntethetők. Nézzük milyen felületeket és szintvonalakat kapunk n különböző eseteire.

n=1

Ebben az esetben a kétváltozós függvény kúpfelületet határoz meg, melynek minden szintvonala kör. Ezeket ábrázolva koncentrikus köröket kapunk:

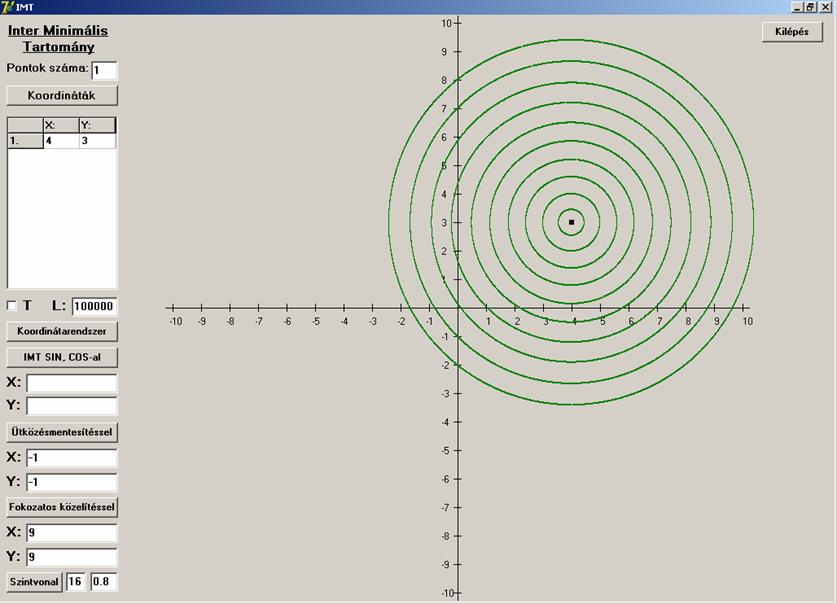
Nemcsak szintvonalakból, hanem tengelymetszetekből is következtethetünk a felületek alakjára. Tudjuk, hogy a kúpfelület síkmetszetei másodfokú görbék abban az esetben, ha a sík nem halad át a csúcspontján. (Ha tengelyre merőleges akkor kör, ha tengellyel párhuzamos, akkor hiperbola, ha az alkotójával párhuzamos parabola, egyébként ellipszis.) Ha a sík áthalad a csúcsponton akkor a metszet elfajult másodrendű görbe lesz. (Pont akkor, ha csak egy közös pontja van a felülettel, egyenes akkor, ha a sík egy alkotójában érinti a kúpot, egyébként egymást metsző egyenes-pár.) Most ez utóbbi esetet ábrázoljuk. Azaz vegyük az (x, z) koordinátasíkkal való metszetét és rajzoljuk az (x, y) síkra. Ezt a piros törött vonal jelzi, mely V alakú. Koordinátageometriából tudhatjuk, hogy ez az abszolút-értékes függvénynek () a képe, melynek az origóban töréspontja van, azaz itt nem deriválható.

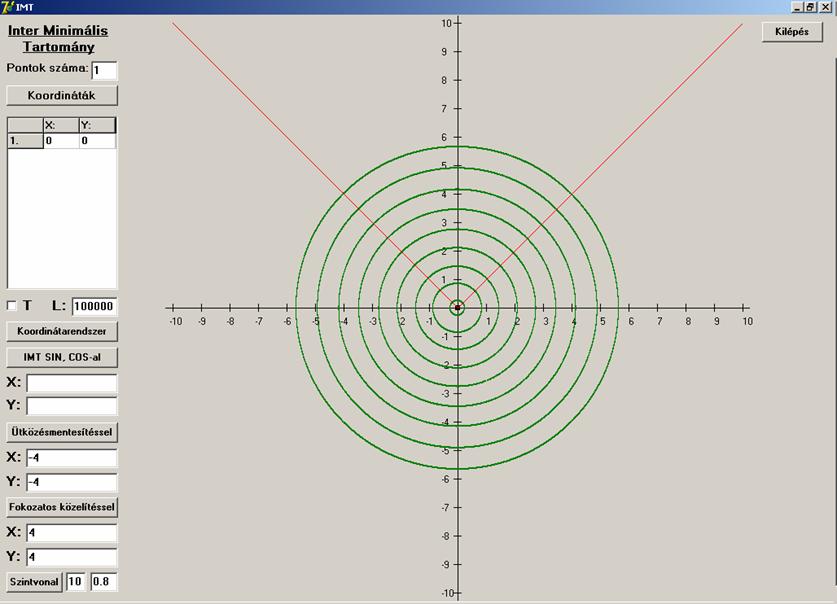
Így függvénytanilag a kúpfelület egy folytonos, minden pontjában konvex (érintő síkjának az egyik oldalára eső) felület, amely a csúcspontja kivételével minden pontjában differenciálható is. (A csúcspontjára végtelen sok olyan sík illeszthető, melynek a kúppal csak egy közös pontja van, azaz nincs egyértelmű érintő sík.)

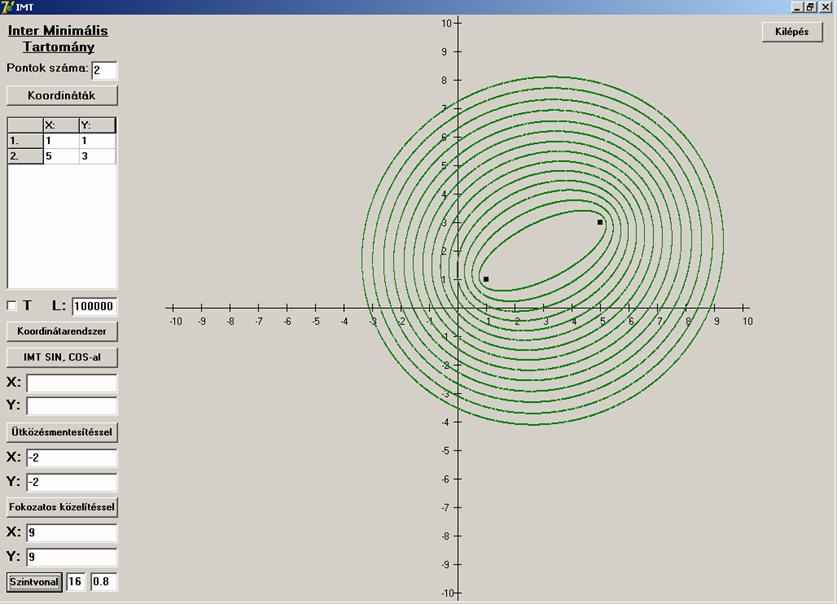
n=2

Ebben az esetben csak kúpszerű (jobb híján nevezzük így) felületet kapunk, melynek két „csúcspontja” van a megadott pontok felett, a két pont távolságával egyező magasságban. A kúphoz hasonlóan konvex, de a két csúcspontjában nem differenciálható. A két pont között a felület egy egyenes szakaszt tartalmaz, amely nem más, mint egy elfajult ellipszis, olyan, amelynek paramétere a két pont távolsága. Minden más esetben a metszete ellipszis lesz:

Nézzük két pontra is a tengelymetszetet:

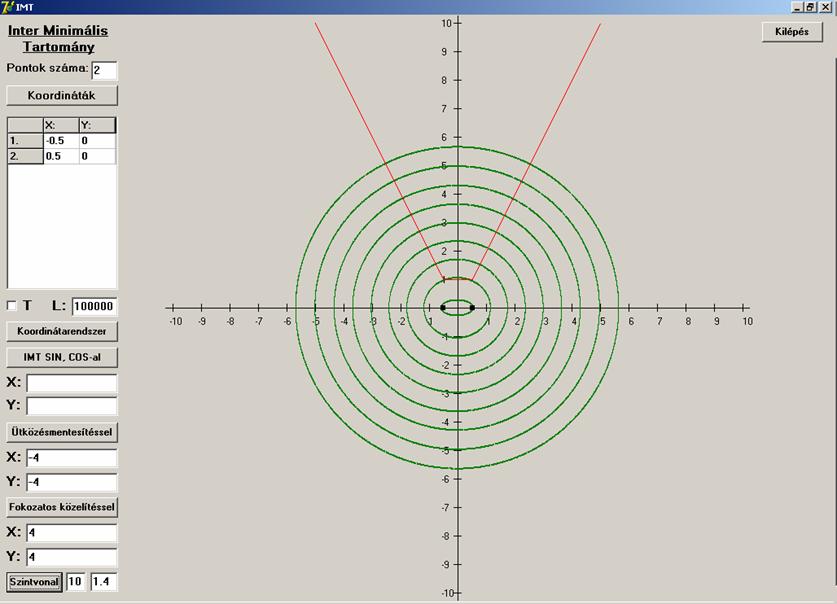
Egy összetettebb abszolút-értékes függvényt kapunk, ami persze nem olyan bonyolult. Az adott két pontban töréspontja van, közte az x tengellyel párhuzamos, azaz konstans. Ebben a két pontban nem deriválható, akárcsak a vizsgált kúpszerű felület sem. Az abszolút-értékes függvény egyenlete:

Ennek szakaszonkénti egyenletei:

y = -2x (Ha x<-0.5.)

y = 1 (Ha -0.5<=x<=0.5.)

y = 2x (Ha x>0.5.)

n=3

Ha nem zavaró, használhatjuk a továbbiakban keletkezett felületeket is kúpszerűnek. Pongyolán fogalmazva ezt n darab kúp összegének mondhatjuk. Itt is követtem az IMT meghatározás lépéseit. Legyen először a három pont egy egyenesen. A fokozatos közelítés módszerével kapott megoldást is feltüntettem a szintvonalakon (vastag zöld vonal).

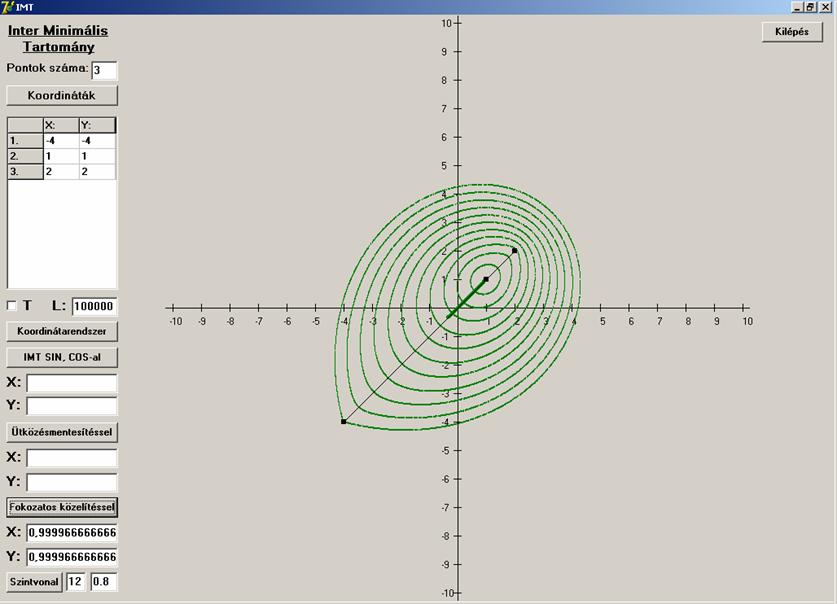
Most legyen a három pont által meghatározott háromszög egyenlő szárú és derékszögű:

Majd általános háromszöget határozzanak meg.

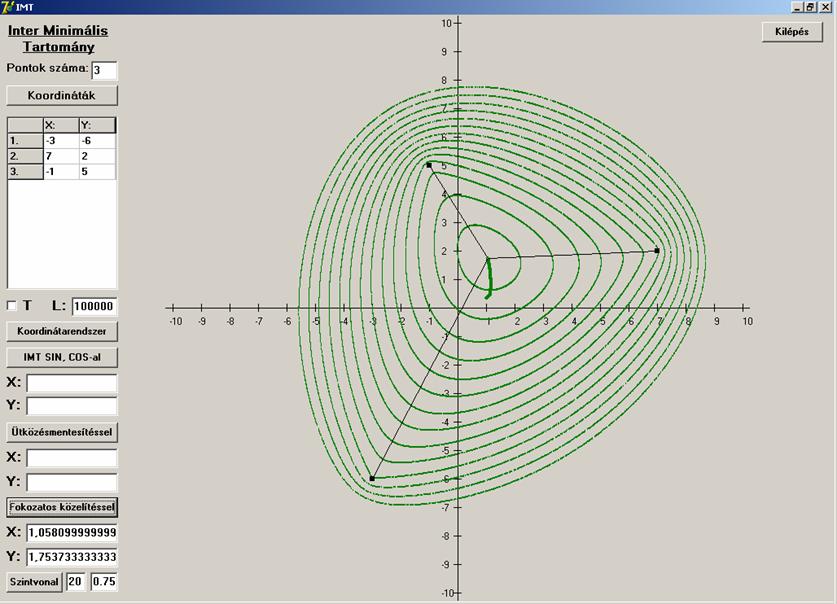
Itt is megnézzük mi a helyzet kollineáris pontok esetén a tengelymetszettel:

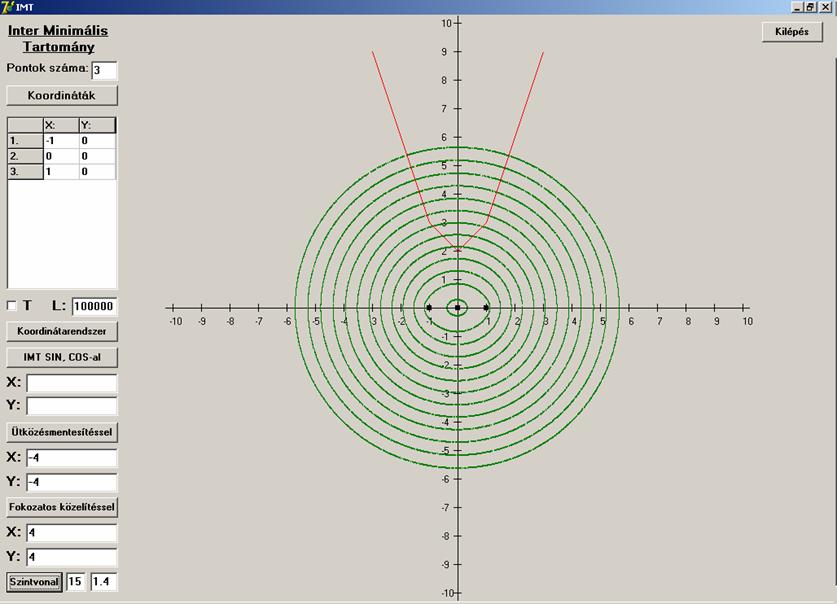
Egy törött vonal a metszet, amelynek értelemszerűen három töréspontja van. Most is megadható az abszolút-értékes függvény egyenlete:

Valamint a szakaszonkénti egyenletek:

y = -3x (Ha x<-1.)

y= -x+2 (Ha -1<=x<0.)

y = x+2 (Ha 0<=x<1.)

y= 3x (Ha x>=1.)

n=4

Konvex négyszög esete:

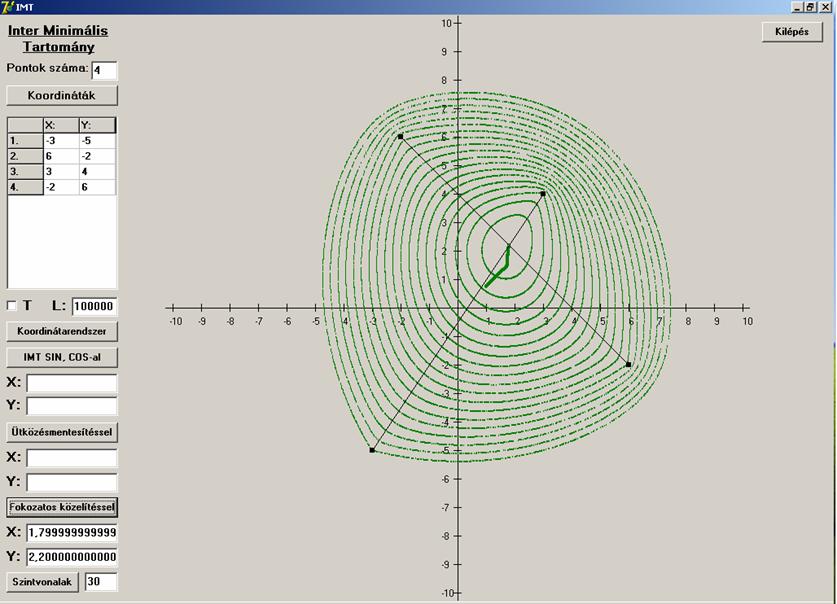
Konkáv négyszög esete:

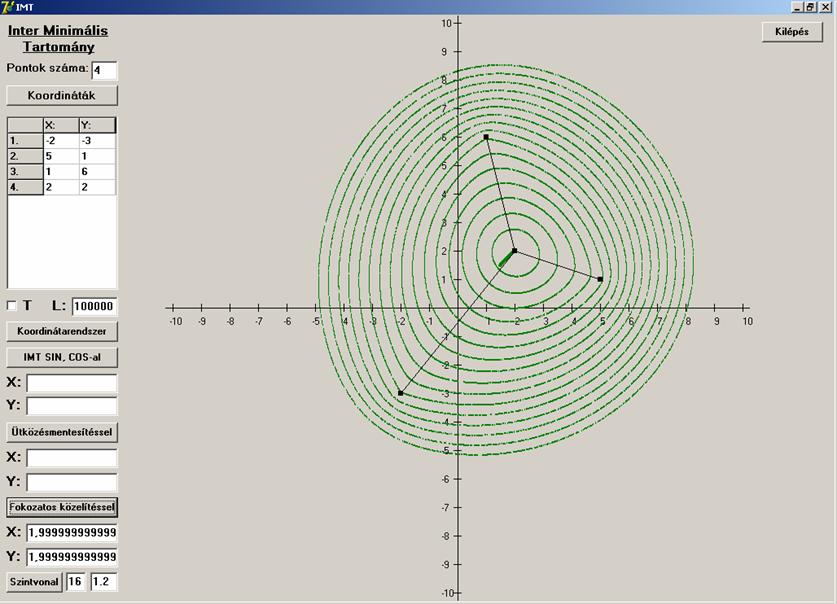
Itt is megnézzük mi a helyzet kollineáris pontok esetén a tengelymetszettel:

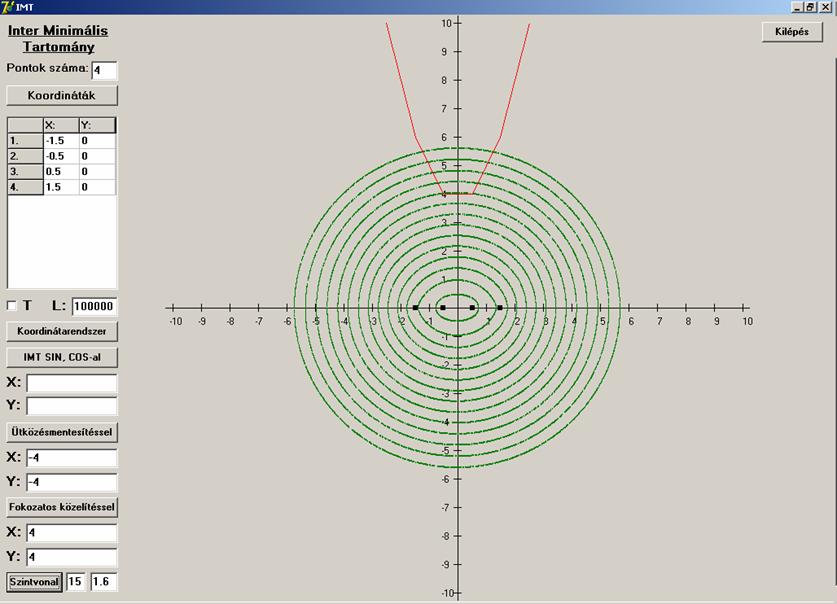
Semmi meglepő. Itt is törött vonalat kapunk, négy törésponttal, mely egy négy tagot tartalmazó abszolút értékes függvényt határoz meg. Képlete:

A szakaszonkénti egyenletek is egyszerűek:

y = -4x (Ha x<-1.5.)

y= -2x+3 (Ha -1.5<=x<-0.5.)

y= 4 (Ha -0.5<=x<0.5.)

y= 2x+3 (Ha 0.5<=x<1.5.)

y= 4x (Ha x>=1.5.)

n=5

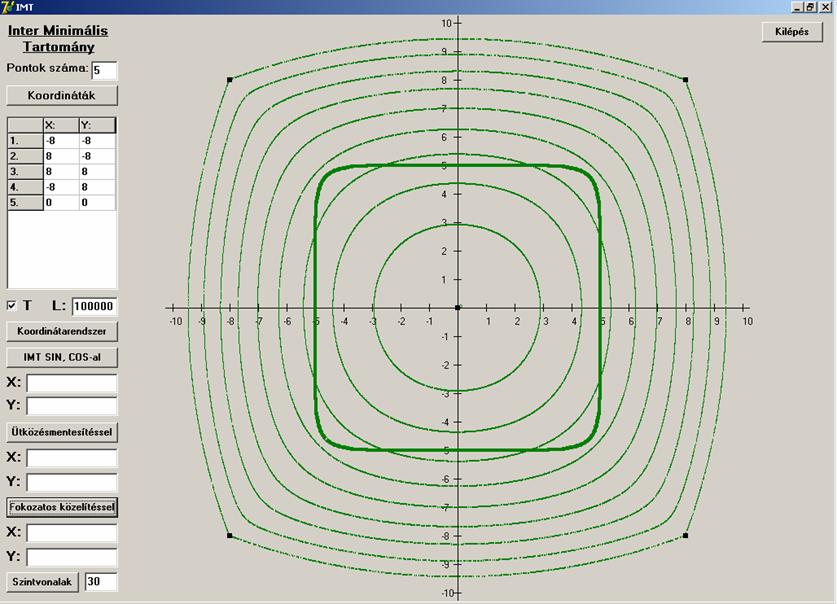
Egyszeresen konkáv, egy négyzet csúcsaiban és a középpontjában vannak a pontok. Az IMT-t (amely területről nem mozdul el az I, ha újabb pontot veszünk a meglévőkhöz) is megrajzolva:

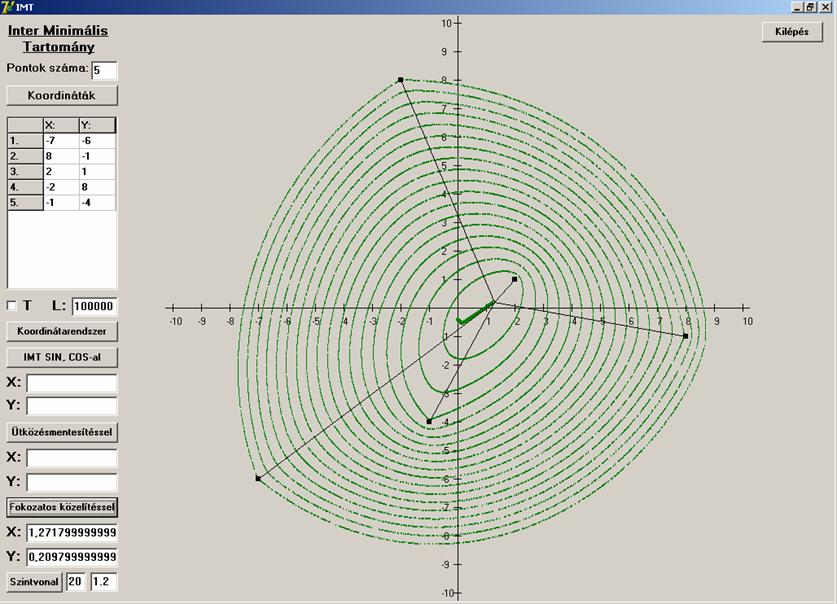
Két nagyszögű, konkáv eset:

Kétszeresen konkáv eset:

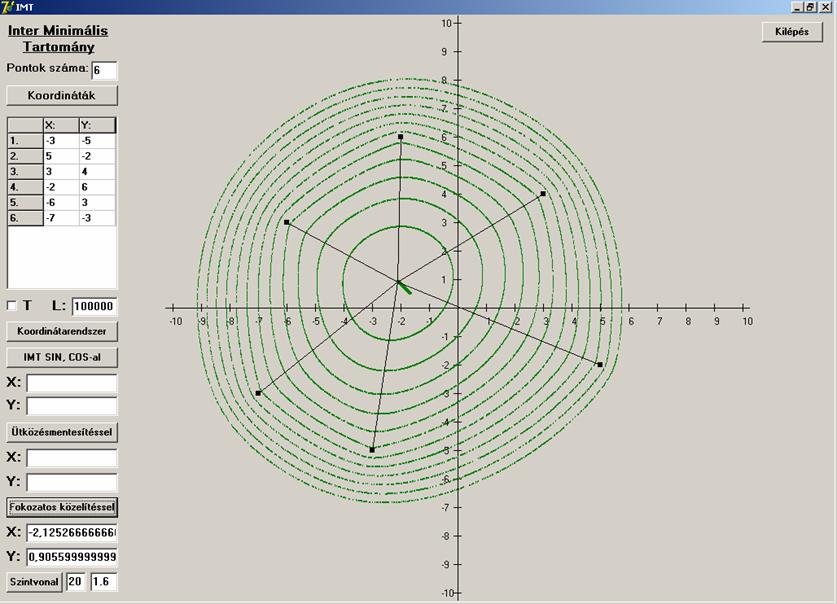
n=6

Konvex hatszög esete:

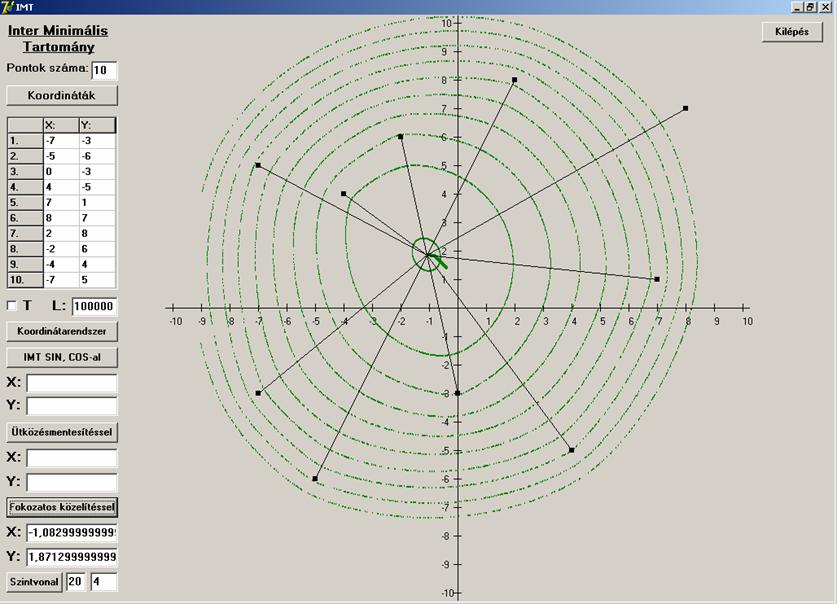
n=10

És végül egy tízpontos esetet nézzünk meg:

Összegezve jól látható, hogy azokban az esetekben, amikor a szintvonal (a metsző sík) átmegy egy ponton az n közül, a keletkezett görbének csúcspontja van, azaz nem differenciálható. Ha a szintvonalak megfelelően sűrűk, illetve beválasztjuk a csúcsokon áthaladó síkokat, látható, hogy felületünk n pont kivételével differenciálható és minden pontjában konvex, a fentebb leirt értelemben. Nagy segítséget adott ennek belátására a speciális esetekben felvett tengelymetszetek, amelyek abszolút-értékes függvények voltak (Ezekkel a függvényekkel egy külön lapon még foglalkozni fogok.)

Következő lap: http://gorbem.hu/MT/Izogonalis6.htm