Izogonális pont (3)

Egy geometriai szélsőérték feladat

Feladat: Adott a síkban n darab pont. Keresendő az a pont, amelyből az adott pontokba húzott szakaszok hosszának az összege – a sík bármely pontjára nézve – a lehető legkisebb.

Folytassuk tovább a vizsgálódást, ezúttal az n=5 esetre. A feladat szempontjából a következő esetek tűnnek lényegesen különbözőknek:

1. Kollineárisak.

2. Az öt pont konvex burka háromszög.

3. Az öt pont konvex burka négyszög.

4. Az öt pont konvex burka ötszög.

Az majd a későbbiekben kiderül, hogy jó volt-e a választás, illetve az, hogy az eseteknek van-e lényegesen különbözőnek számító alesete. Főleg a fokozatos közelítés módszerével vizsgálom az eseteket. Néha az első módszert is kipróbálom.

1. Kollineárisak.

Jelöljük a pontokat A, B, C, D és E -vel, ilyen sorrendben elhelyezkedve az egyenesen. Az a gondolatunk, hogy ekkor a megoldás a középső (C) pont. Az IMT mértéke pedig az AE és BD szakaszok összege. Nézzük megerősít-e ebben a közelítő eljárás.

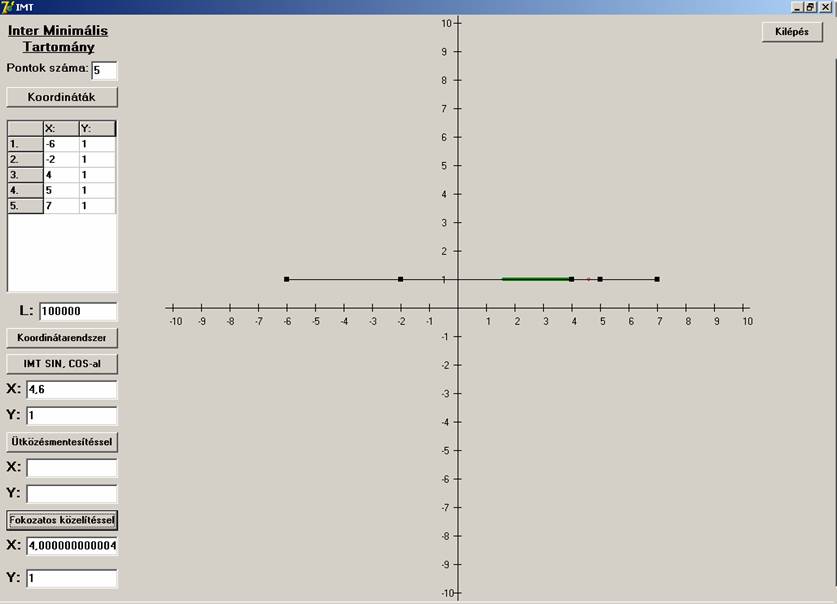
Igen, valóban a középső pont lesz az I, az első (szögfüggvényes) viszont nem adja a helyes eredményt. Változtassuk meg a koordinátareprezentációt, az első használhatatlansága még jobban szembetűnő:

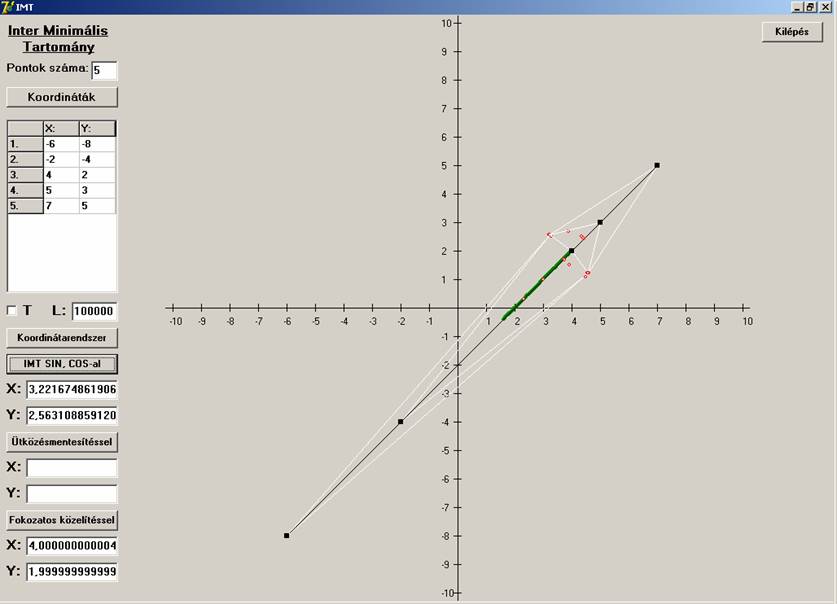
Látható (fehér szakaszok), hogy még a pontok egyenesére sem esik a közelítő érték, vagyis használhatatlan az eljárás.

2. Az öt pont konvex burka háromszög.

Ebben az esetben további aleseteket különböztethetünk meg. A háromszöget alkotó 3 ponton kívül van még két pontunk, melyeket elhelyezhetünk:

A) A háromszög egy oldalán (négy pont kollineáris).

B) A háromszög két oldalán (kétféleképpen van három kollineáris pont a kerületen).

C) A háromszög egyik oldalán és a belsejében (van három kollineáris pont a kerületen, vagy a kerületen és a belsejében lévő pontok által is van kollineáris).

D) A háromszög belsejében (kétszeresen konkáv ötszöget alkot az öt pont).

A.

Négy kollineáris pont esetén először az ötödik pont legyen kissé távolabb a négy egyenesétől. Ekkor az első és a harmadik közelítő eljárás is jól működik:

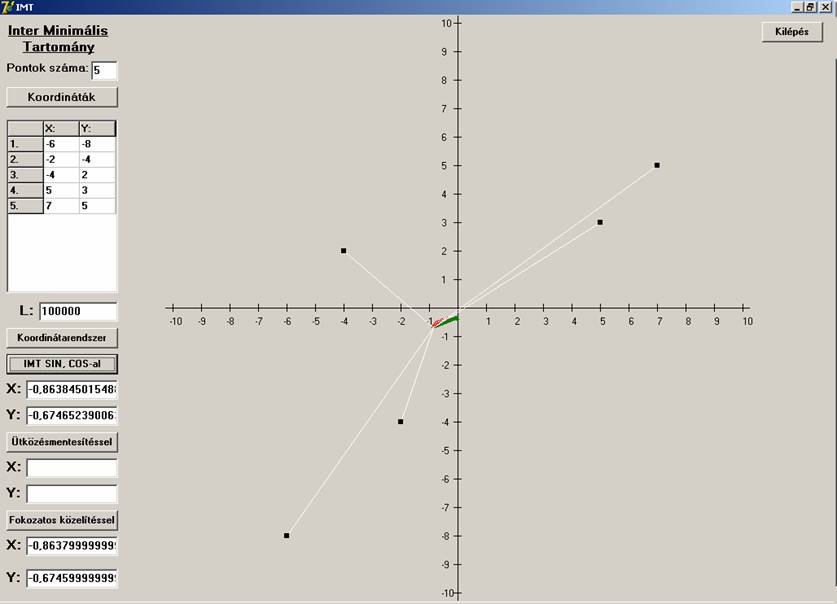
Legyen az ötödik pont relatíve közel a négy pont egyeneséhez. Ebben az esetben az várható, hogy a megoldás ez az ötödik pont lesz. Vajon ekkor is jó az első eljárás?

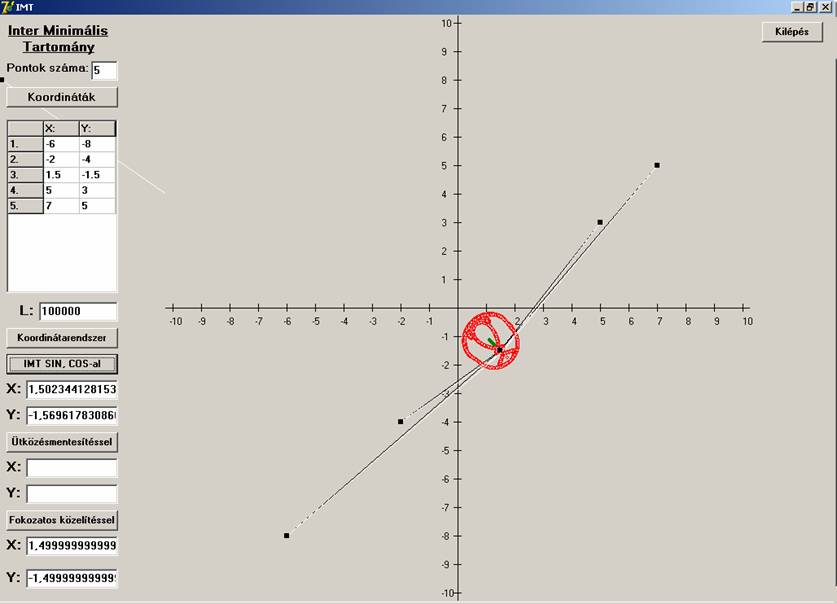
Úgy látszik az első eljárás furcsán viselkedik akkor, ha megoldás egy pont az eredeti pontok közül. Az előző esetben épp ez látható. Ugyanakkor felvetődik a kérdés, hogy milyen közel kell lenni az ötödik pontnak az egyeneshez, esetleg valamelyik ponthoz, hogy a megoldás ez az ötödik pont legyen. Másképp fogalmazva: adjuk meg azt a területet, amelyről az I nem mozdul el, akárhova is választjuk az ötödik pontot. Erre a kérdésre hamarosan visszatérünk.

B.

Legyen a további két pont a háromszög két oldalán Ebben az esetben mindkét eljárás ugyanazt szolgáltatja:

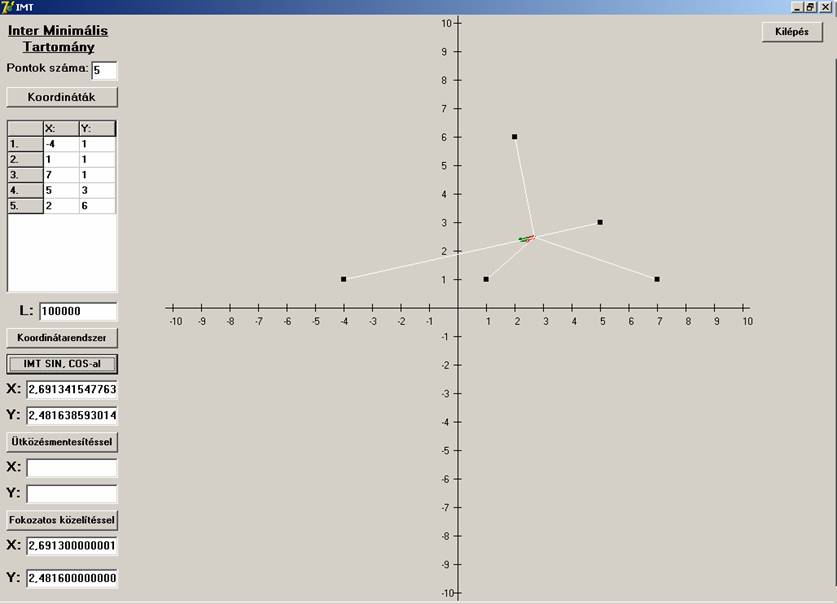
C.

Most nézzük mi a helyzet, ha a két pont a háromszög egyik oldalán és a belsejében található:

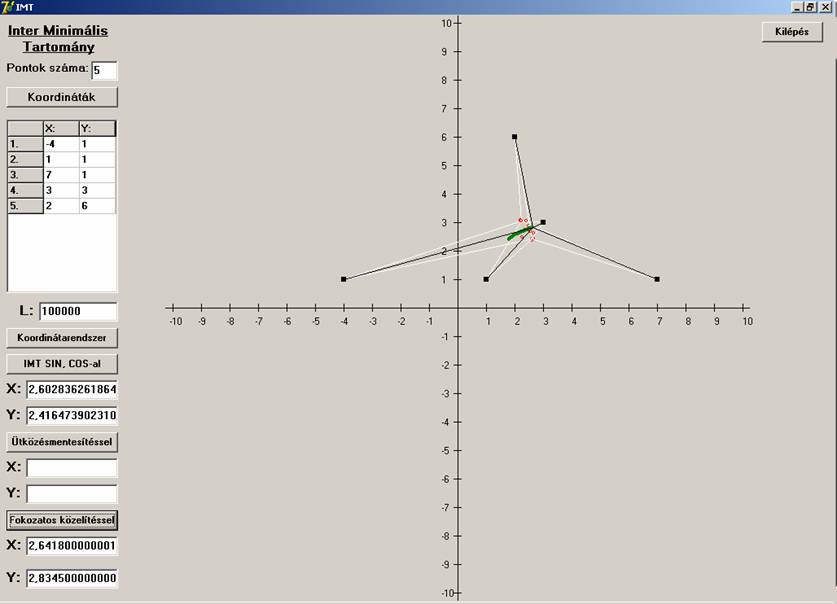
Az első eljárás helytelen eredményt adott. Látható, hogy többszöri futtatás esetén különböző, a helyes eredménytől mérhetően különböző pontokhoz közelít. Mi a helyzet, ha a belső pont is kollineáris a kerületen lévő megfelelő két ponttal:

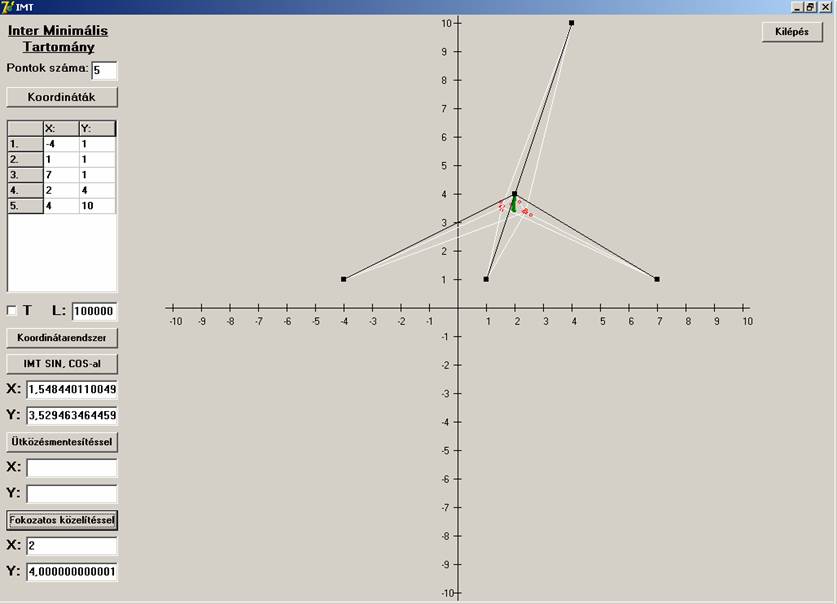
Látható, hogy a helyzet ugyanaz. Az első eljárás használhatatlan.

D.

Utolsóként a két pont legyen a háromszögön belül.

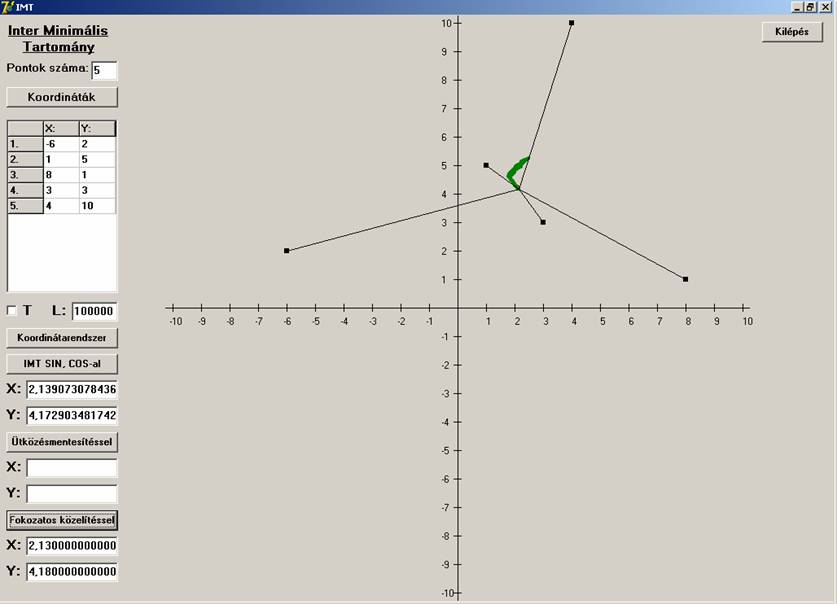
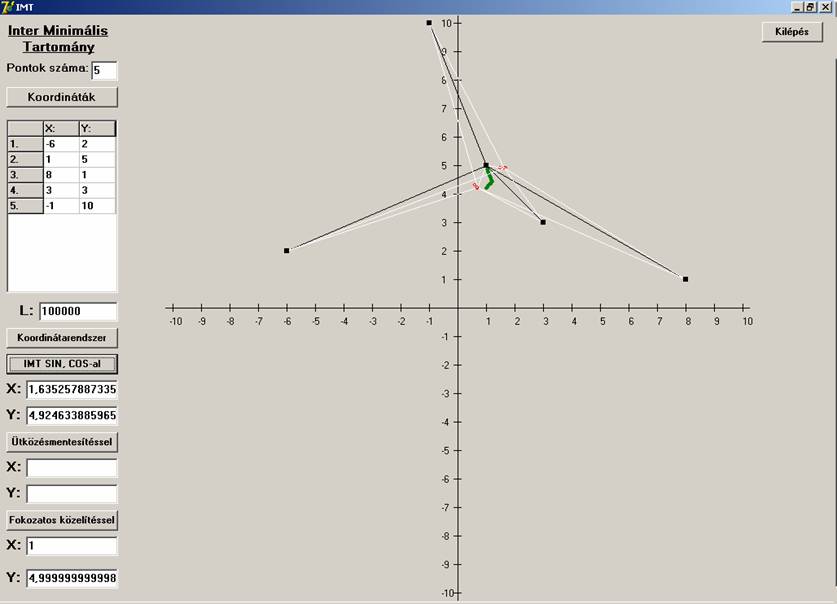
Semmi különbség. Az első eljárás nem jó.

3. Az öt pont konvex burka négyszög.

Itt két alesetet vizsgálhatunk a szerint, hogy az ötödik pont hol található.

A) Az ötödik pont a négyszög kerületén van (van három kollineáris pont a kerületen),

B) Az ötödik pont a négyszögben van (konkáv ötszög esete). Itt az is vizsgálható, hogy az ötödik pont a négyszög átlójának metszéspontja-e vagy nem.

A.

Legyen tehát az ötödik pont a négyszög kerületén.

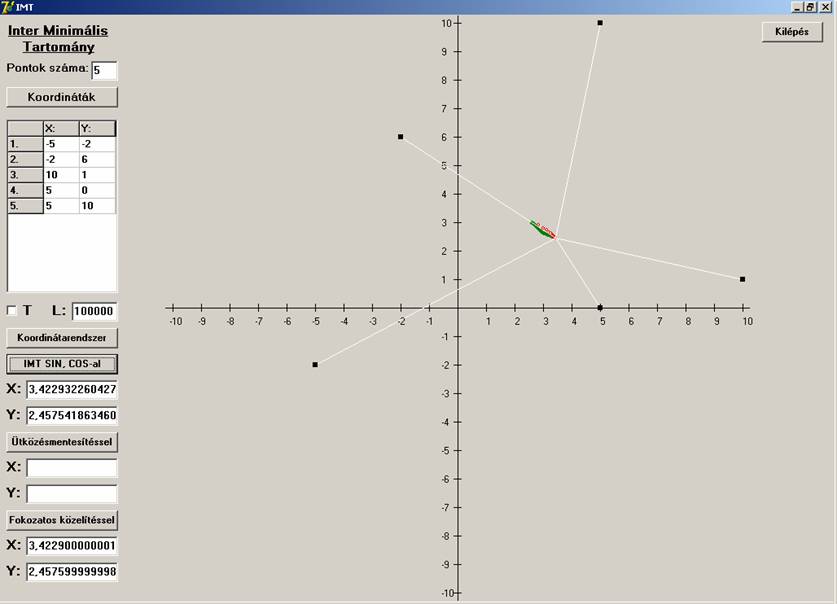
Úgy néz ki, hogy azonos megoldásokat szolgáltatnak. De most legyen a négyszög nagyon „lapos”, azaz legyen 180 fokhoz közeli szöge:

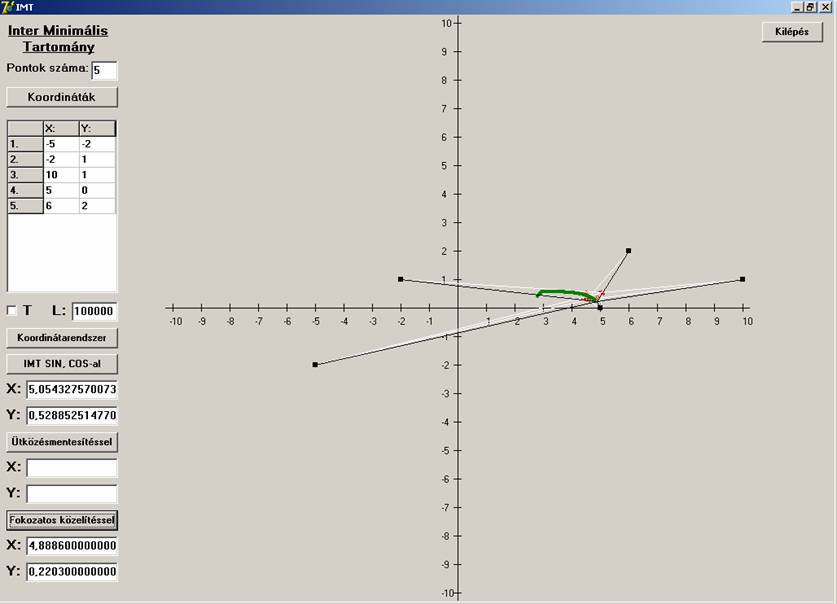
Az első eljárás nem lett jó.

B.

Legyen az ötödik pont a négyszög belsejében. Először ne a négyszög átlóinak metszéspontja:

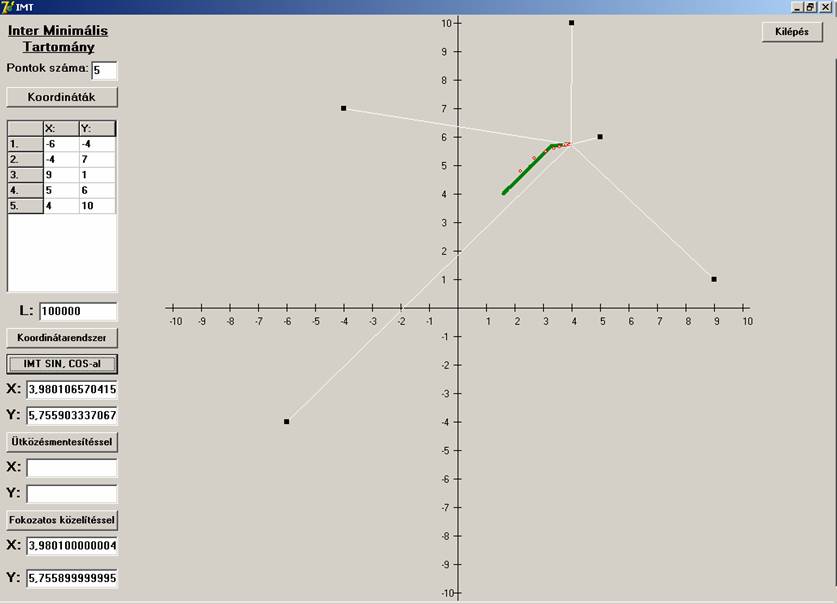
Mindkét eljárás jó eredményt szolgáltatott. Második alesetként a pont legyen az átlók metszéspontja:

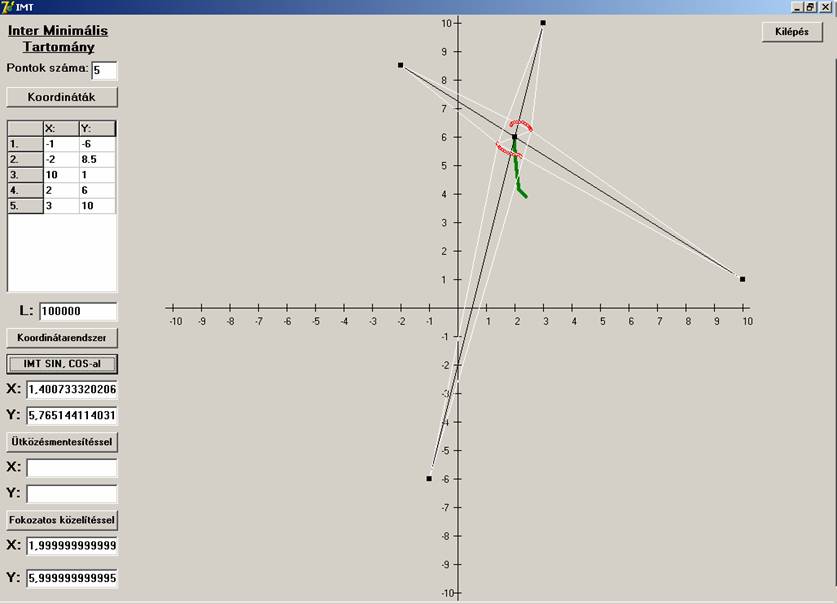
Az első eljárás most is megbukott.

4. Az öt pont konvex burka ötszög.

Ebben az esetben csak annyit fogunk variálni, hogy először egy olyan ötszöget választunk, amelynek szögei közel azonosak:

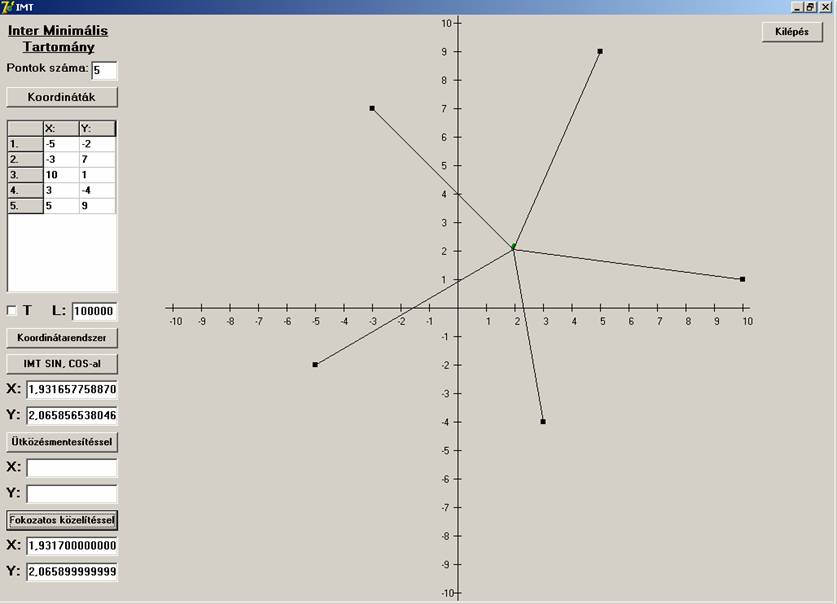
Mindkét eljárás jól működik. Most vegyünk egy olyan ötszöget, melynek van 180 fokhoz közeli szöge:

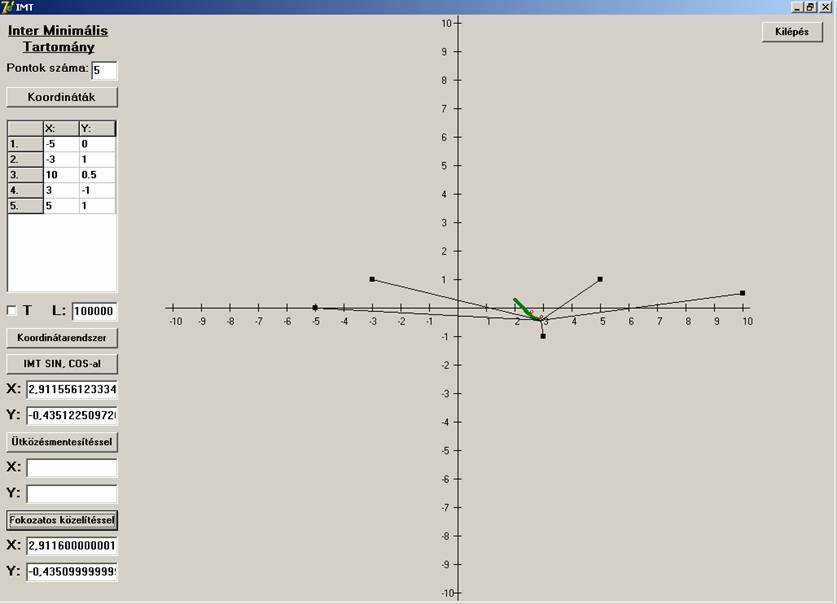
Ekkor is mindkét eljárás „ugyanazt” az eredményt adta.

Összességében elmondhatjuk, hogy a fokozatos közelítő módszere mindig jó eredményeket produkált. Az első (egységvektoros) viszont több esetben hibásan konvergált, újra futtatva ugyanolyan kezdeti feltételek ellenére, más-más pontot szolgáltatott, azaz valójában nem is konvergált. A továbbiakban nem fogom használni.

A második eset (a konvex burok háromszög) A) pontjában (négy pont kollineáris) megfogalmazódott kérdésként az, hogy van-e olyan tartomány a síkon, amelyről az I nem mozdul el, bárhova is vesszük fel az ötödik pontot. A következő részt ilyen kérdések megválaszolásának szánom.

Következő lap: http://gorbem.hu/MT/Izogonalis4.htm