Izogonális pont (2)
Egy geometriai szélsőérték feladat
Feladat: Adott a síkban n
darab pont. Keresendő az a pont, amelyből az adott pontokba húzott szakaszok
hosszának az összege – a sík bármely pontjára nézve – a lehető legkisebb.
A szakirodalom bővelkedik a feladat n<5 esetének megoldásában. Az első részben (Izogonális
pont (1)) ezeket foglaltam össze, illetve kiegészítettem az IMT mértékének
kiszámításával az n=3 esetre. Ebben
a második részben közelítő módszereket
tesztelek. Az n=1 és n=2 esetekre semmiféle közelítő
eljárásnak nincs értelme, hiszen a megoldás szinte triviális. Ezért csak n=3 és n=4 esettel foglalkozom. Erre azért van szükség, mert közelítő
módszereknek n bármilyen véges
érékére és bármilyen pontelrendezésre helyes eredményeket kellene adni. n=3 és n=4 -re viszont tökéletesen ismerjük a
megoldást, melyet összevethetünk a közelítő eljárás eredményével, így
megítélhetjük a közelítő módszer helyességét. Írtam egy programot Delphi-ben, amellyel három módszer próbálható ki. Lássuk
ezeket:
Az első közelítő eljárás.
Térjünk vissza az első rész azon egyenleteihez, melyek
a távolságösszegek és azok deriváltjait tartalmazzák. Emlékeztetőül:
A
parciális deriváltak:
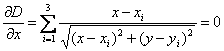
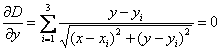
Ez
utóbbit trigonometrikus egyenleteknek is felfoghatjuk:
és
ahol a
szögek az I -ből
a pontokba mutató helyzetvektorok irányszögeinek tekinthetők. Az egyenletek azt
fejezik ki, hogy az I -ből a pontok felé mutató egységvektorok összege 0-vektor. Itt említeném meg, hogy a
probléma Pólya György-féle mechanikai megoldásának
(szemléltetésének) az alapját is ezek az egyenletek szolgáltatják, ahol egyenlő
nagyságú erők egyensúlyával választódik ki a keresett pont. Kíváncsi voltam,
hogy ez mennyire adja helyesen az I -t az n=3
különböző eseteire. Nézzük az algoritmust:
Az algoritmus:
1.
Vegyük kiindulási (aktuális) pontnak a három pont súlypontját, illetve az ide
mutató (aktuális) helyvektort. (Egyébként ez nem feltétlen kötelező, bármely
ponttal illetve helyvektorral kezdhetünk.)
2.
Állítsuk elő az aktuális pontból a pontokba mutató egységvektorokat.
3.
Adjuk hozzá az aktuális helyvektorokhoz az egységvektorokat, az így kapott
helyvektor legyen az új (aktuális) helyvektor.
4.
Valamilyen kritériumtól (ez lehet például lépésszám vagy az utolsó
egységvektorok összegének a nagysága) függően lépjünk vissza a 2. pontra, vagy
fejezzük be az algoritmust, mert elég közel kerültünk az I-hez.
Lássunk akkor n=3-ra
egy-egy példát:
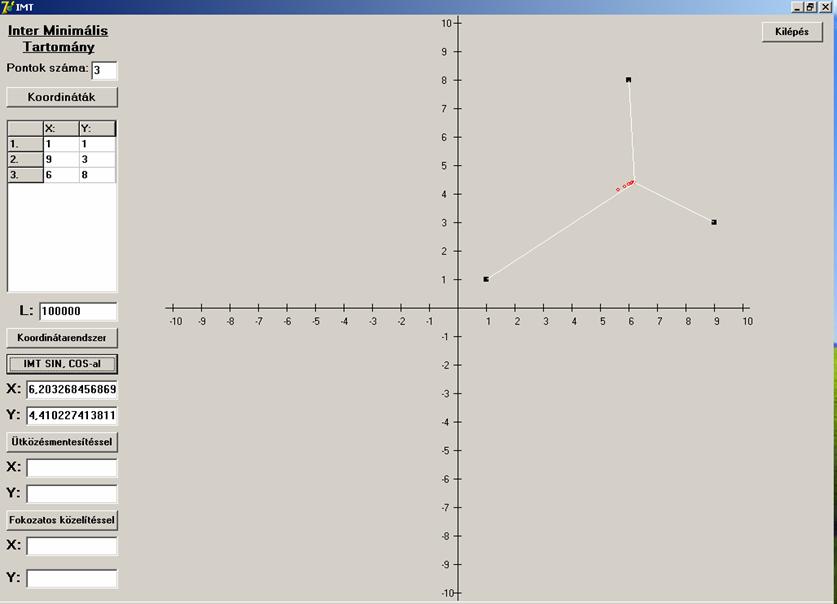
A piros körök az egyes lépések helyét (aktuális
pontjait) jelölik, a fehér szakaszok a megoldásnak felelnek meg. Az x és y koordináták az „IMT SIN, COS-al”
feliratú nyomógomb alatt láthatók. Úgy néz ki, hogy az algoritmus működik. Ebben
a példában a háromszögnek minden szöge kisebb
-nál. De mi a helyzet, ha ez nem
áll fenn? Lássuk:
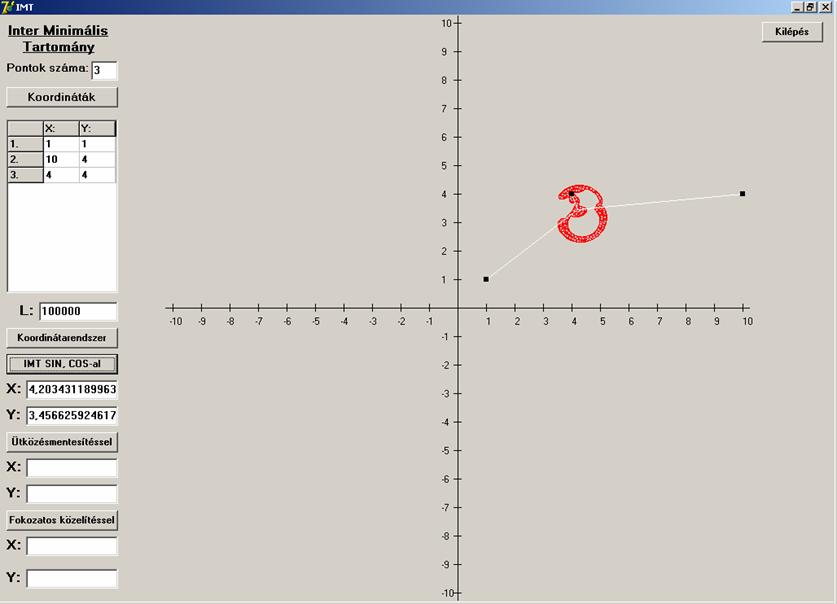
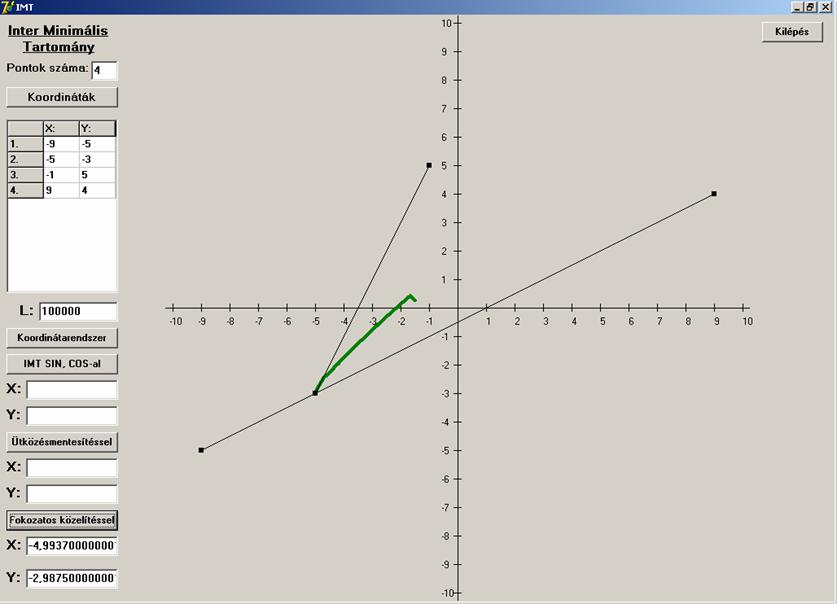
Hát ez egészen szomorú. Az algoritmus nem konvergál,
sőt a megoldást sem adja (ami a
-nál nagyobb szögű csúcs lenne). Nézzünk
egy másik példát is erre az esetre:
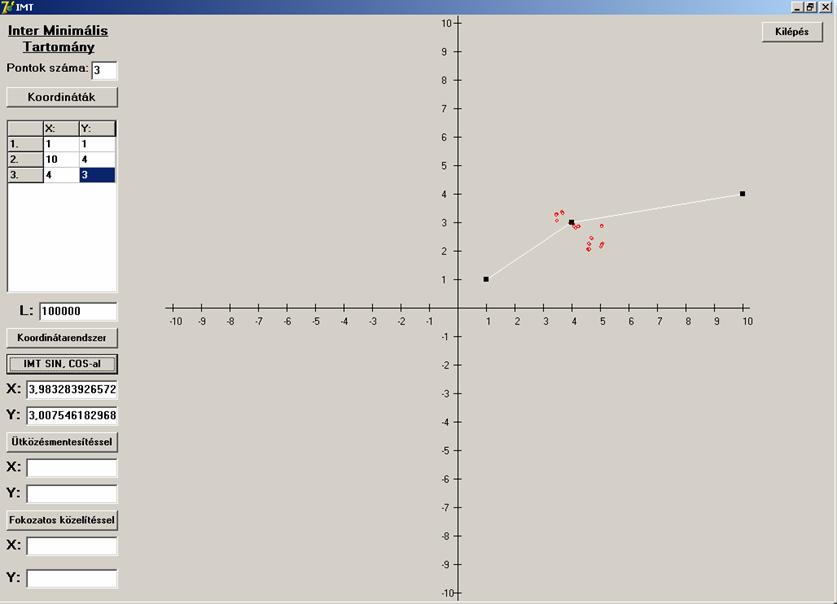
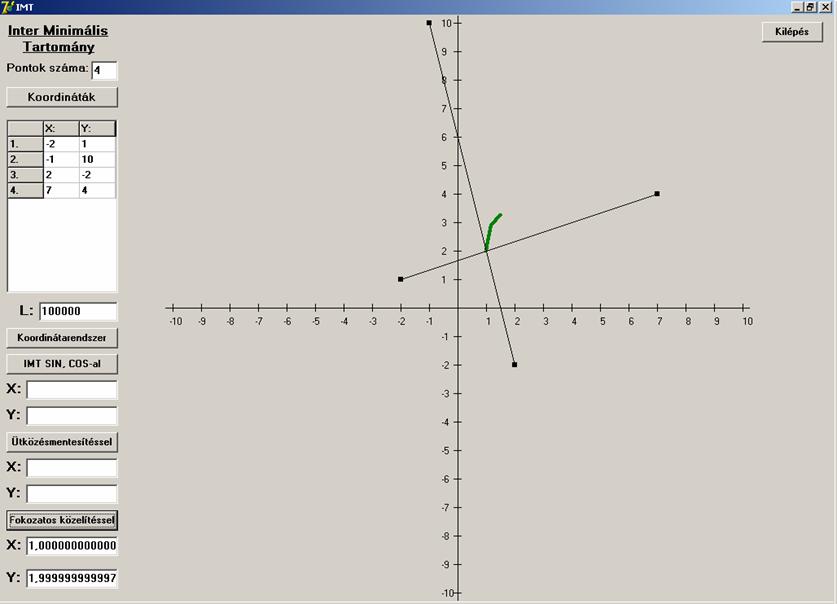
Itt viszont jó közelítést kaptunk. (Pontosságát ne
firtassuk.) Megváltoztattam az előző példában a két darab y=4 -es esetet. Ezt azért célszerű
elkerülni (mármint azt, hogy azonos koordináták legyenek a pontok koordinátái
között), mert ekkor a szögfüggvények hirtelen változásokat szenvednek. Ebből
arra lehet következtetni, hogy nem mindegy melyik pillanatban ér véget az
algoritmus. Az algoritmus ugyanis lépésszám elérésére ér véget. Ha a szükséges
lépésszámot véletlen értékre állítjuk, és többször lefuttatjuk az algoritmust
ugyanarra az esetre, akkor ez nyilvánvalóvá válik:
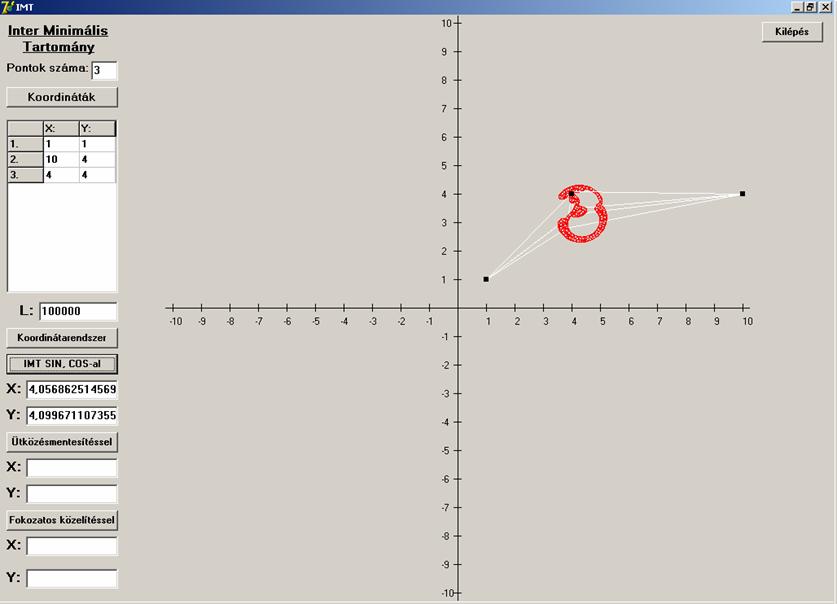
Ahány futtatás, annyiféle végeredmény (fehér
szakaszok).
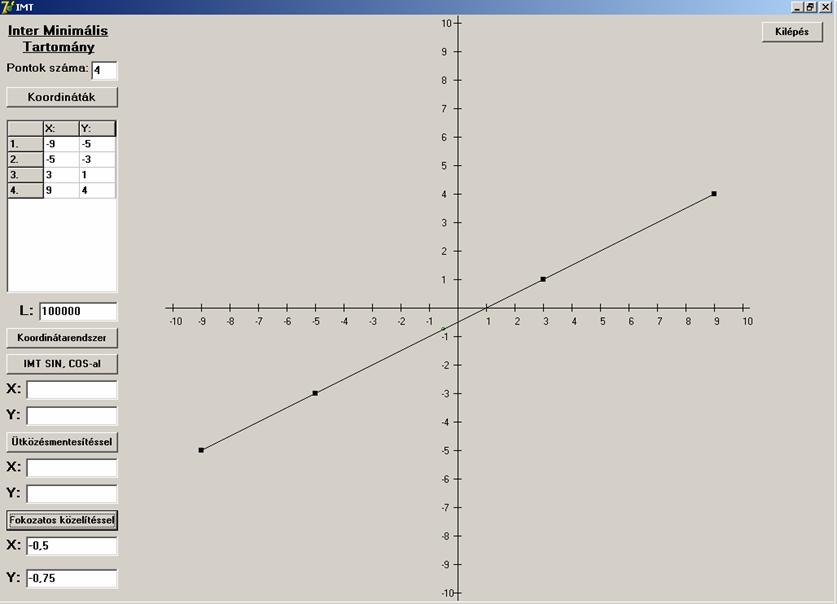
Mi a helyzet, ha a három pont egy egyenesre esik:
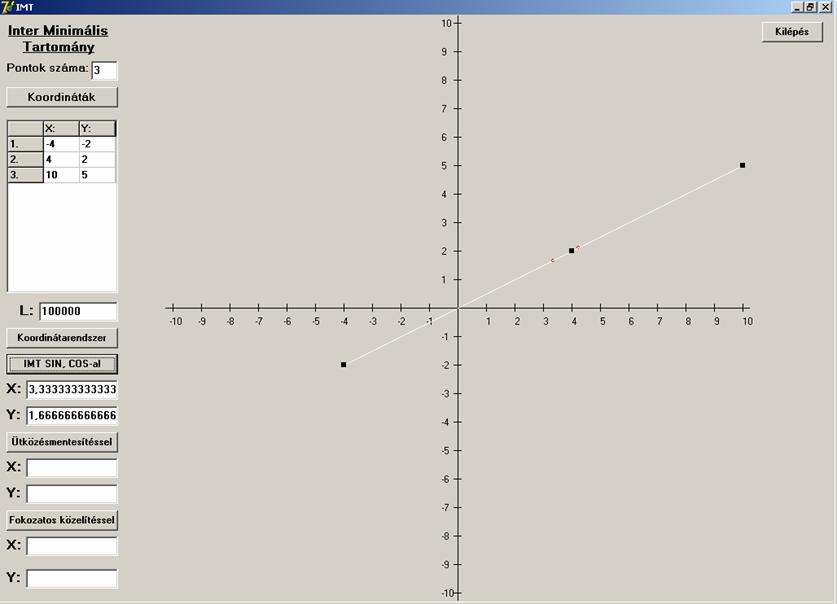
Ez sem stimmel. A (4,
2) pontot kellett volna kapnunk. Tehát ennek az algoritmusnak az
alkalmazhatóságát még meg kell vizsgálni, eredményeit kritikával kell fogadni.
A második közelítő eljárás
Ez az eljárás gyakorlatilag az
ütközésmentesítő algoritmusom lépéseit követi. Mivel minden szóba jövő pontra
kiszámolja az IMT mértékét (a
távolságösszegeket), ezért a közelítésben igencsak bízhatunk.
Az algoritmus:
1.
Vegyük kiindulási (aktuális) pontnak a három pont súlypontját. (Egyébként ez
nem feltétlen kötelező, bármely ponttal kezdhetünk.)
2.
Határozzuk meg az aktuális pont IMT
mértékét.
3.
Válasszunk véletlenül egy új pontot az adott pontok környezetében és határozzuk
meg az új pont IMT -jét.
5.
Valamilyen kritériumtól (ez lehet például lépésszám vagy az utolsó két aktuális
pont távolsága) függően lépjünk vissza a 3. pontra, vagy fejezzük be az
algoritmust, mert elég közel kerültünk az I-hez.
Elsőként legyen olyan a három pont, hogy az általuk
alkotott háromszögnek minden szöge kisebb -nál.
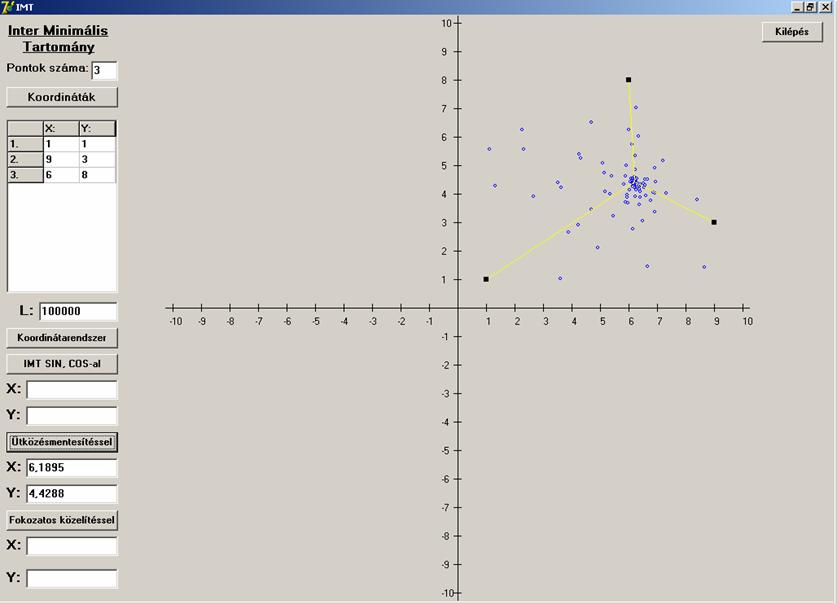
Úgy néz ki, hogy működik. Lássuk a két kritikus
esetet. (
-nál nagyobb szög és egy egyenesen
lévő pontok.)
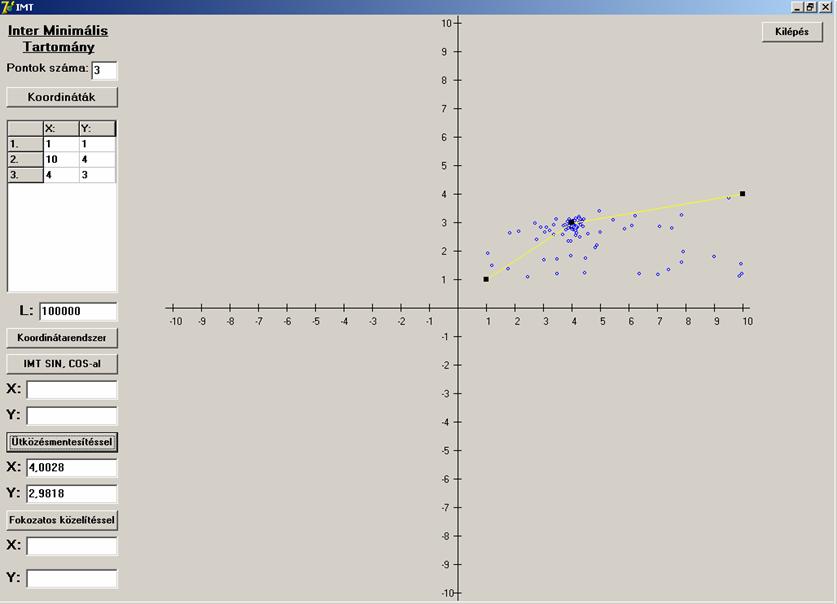
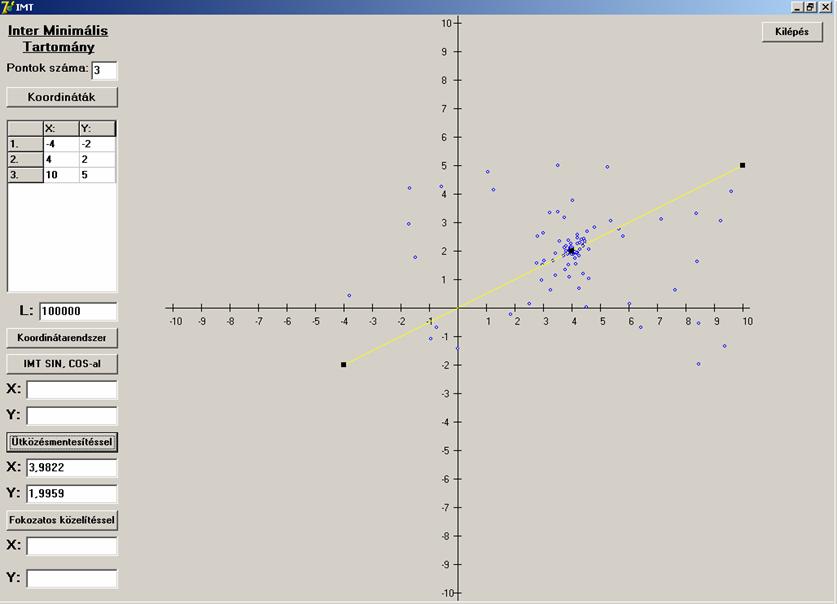
Az algoritmus itt is megfelelőképpen működik.
A harmadik közelítő eljárás
Ez az algoritmus egyesíti az előző kettő jó
tulajdonságait. Határozott konvergenciát mutat, mint az első, de minden pontra
számol az IMT -t mint a második, így itt is bízhatunk a közelítés
helyességében.
Az algoritmus:
1.
Vegyük kiindulási (aktuális) pontnak a három pont súlypontját. (Egyébként ez
nem feltétlen kötelező, bármely ponttal kezdhetünk.)
2.
Határozzuk meg az aktuális pont IMT
mértékét.
3.
Keressük meg az aktuális pont környezetében, tőle meghatározott – de elég kis –
távolságra lévő pontok közül a legjobb tulajdonságú pontot és ez legyen az új
aktuális pont.
4.
Valamilyen kritériumtól (ez lehet például lépésszám vagy az utolsó két aktuális
pont távolsága) függően lépjünk vissza a 3. pontra, vagy fejezzük be az
algoritmust, mert elég közel kerültünk az I
-hez.
Az egyszerűség kedvéért a program az elég kis
távolságra lévő pontokat a négy koordináta irányban keresi. Nézzük a szokásos
esteket. Először hegyesszögű háromszögre:
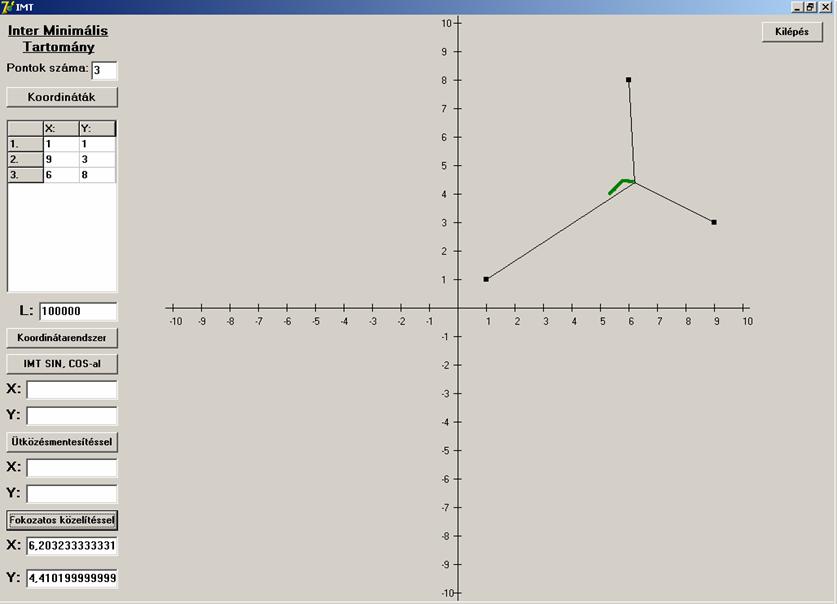
A megoldás jónak tűnik. Nézzük -nál nagyobb szögű háromszögre:
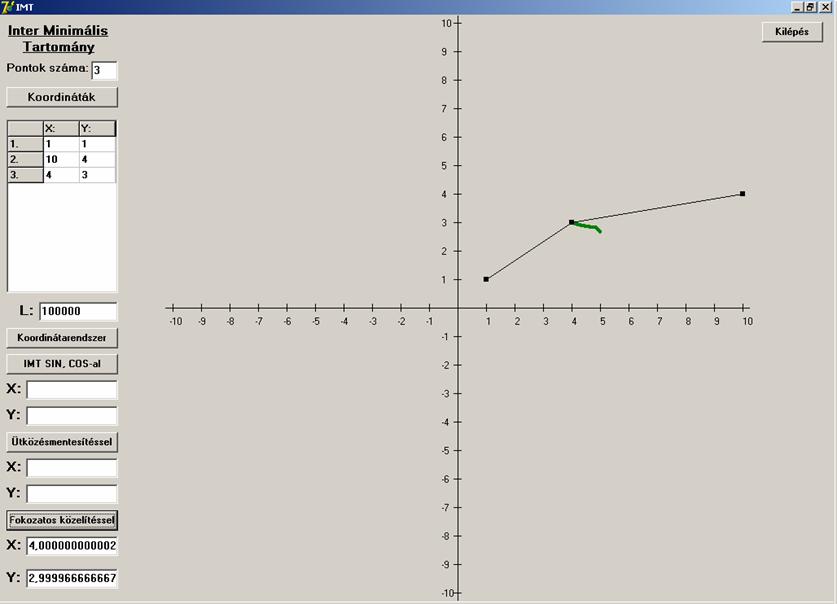
Most is jó ponthoz konvergál. És az utolsó eset,
amikor a három pont kollineáris:
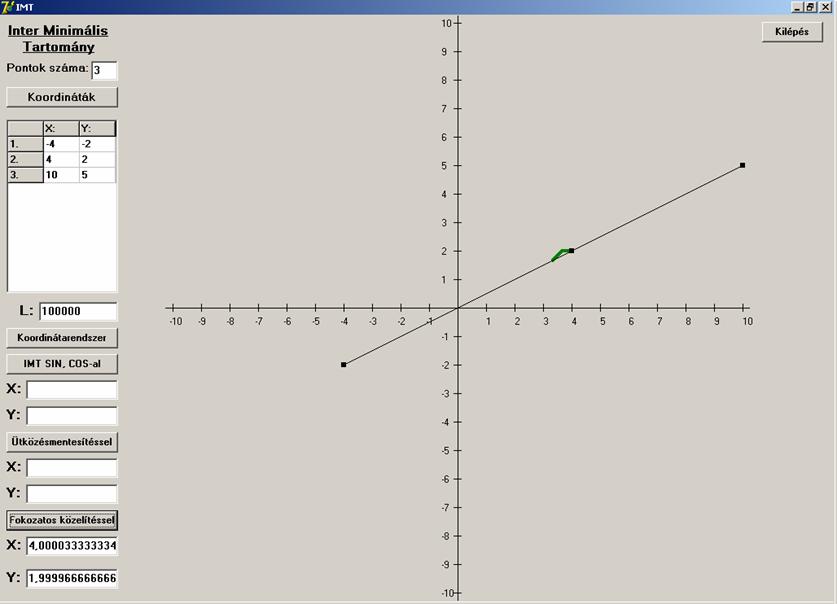
Szintén a jó megoldást szolgáltatta.
A második és harmadik közelítő eljárás tehát jól
működik, míg az első eredményeit kritikával kell fogadni. A programból nem
veszem ki az első eljárást, mert kíváncsi vagyok, hogy háromnál több pont
esetén mikor ad helytelen eredményt.
Lássunk egy-egy olyan screenshot-ot amelyeken egymásra
van vetítve a három módszer. Hegyesszögű- háromszög
esetében nagy a hasonlóság:
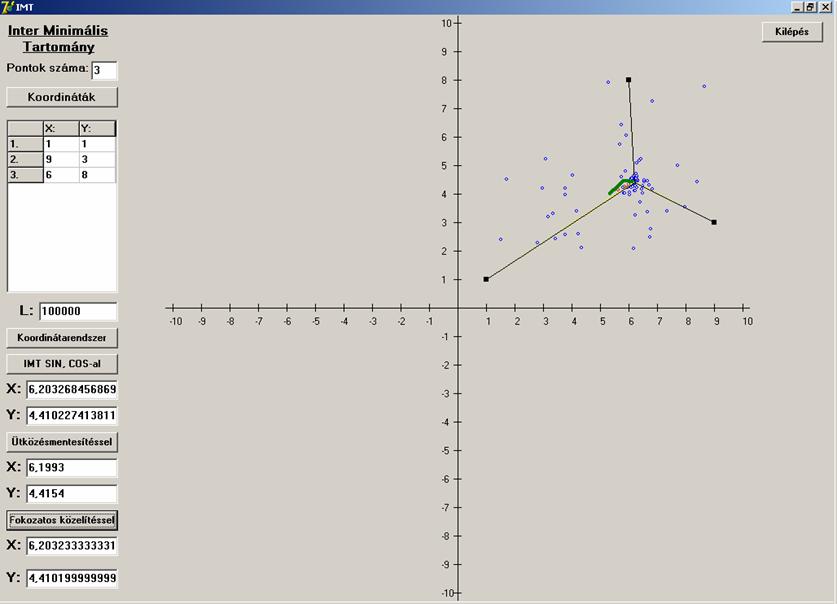
Legyen a háromszögben -nál nagyobb szög:
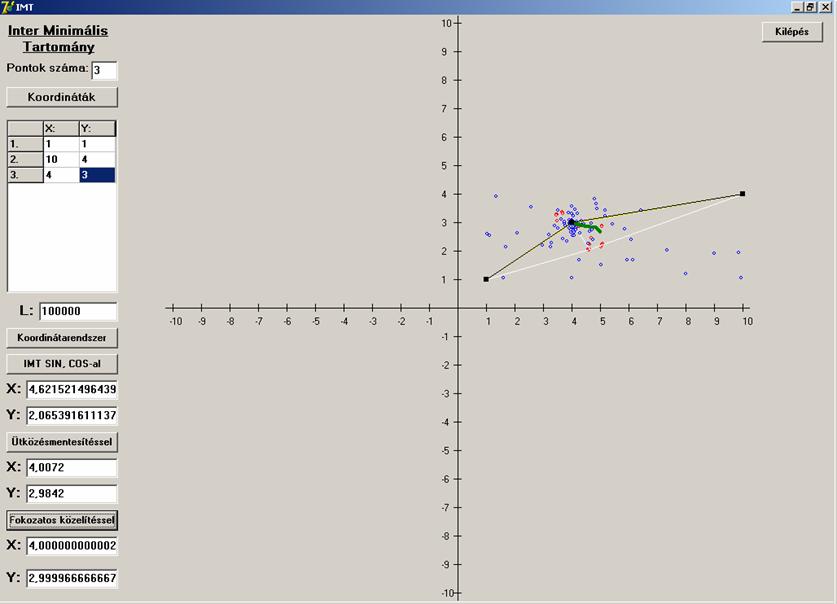
Látható, hogy az első közelítő módszer itt nagyon
eltérő eredményt produkált (fehér szakaszok).
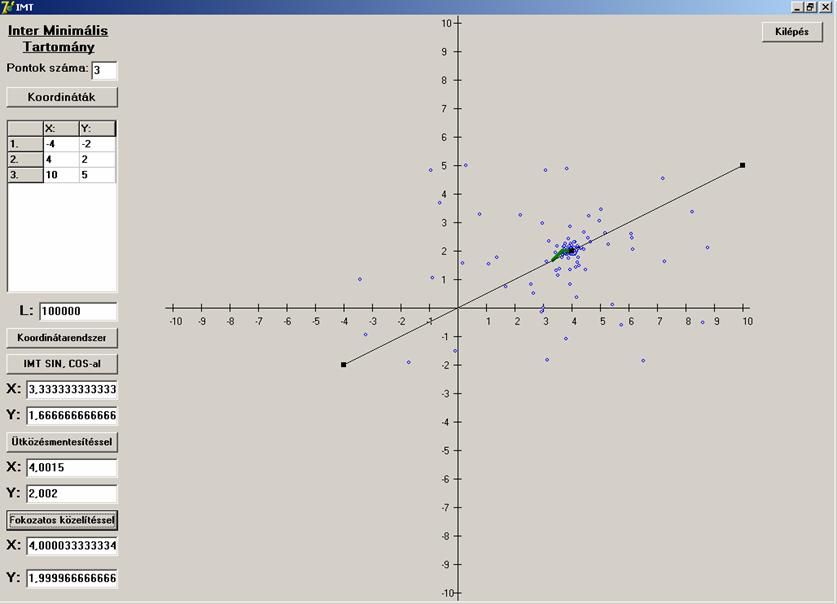
Tehát az első és a harmadik esetben elég közeli
értékeket adtak mindhárom eljárásra, a második esetben viszont durva az eltérés
az első közelítő eljárásnál (fehér szakaszok).
Ezek után térjünk át az n=4 esetre. Mint ahogy azt az első részben is leírtam, négy
lehetséges esettel kell számolni. A négy pont kollineáris,
csak három pont kollineáris a négy közül, a négy pont
konvex négyszöget határoz meg, és a negyedik, amikor konkáv négyszöget.
Mindegyikre lássunk példát először az első algoritmust
használva.
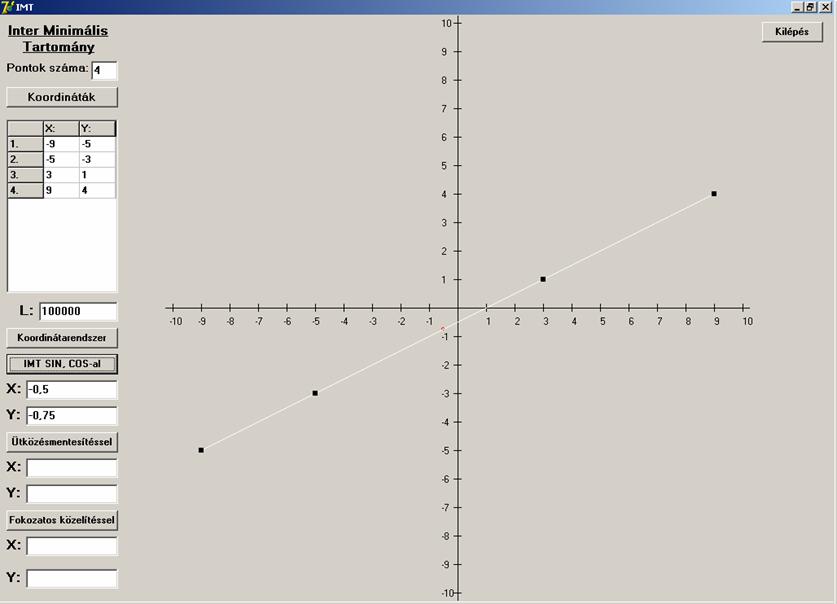
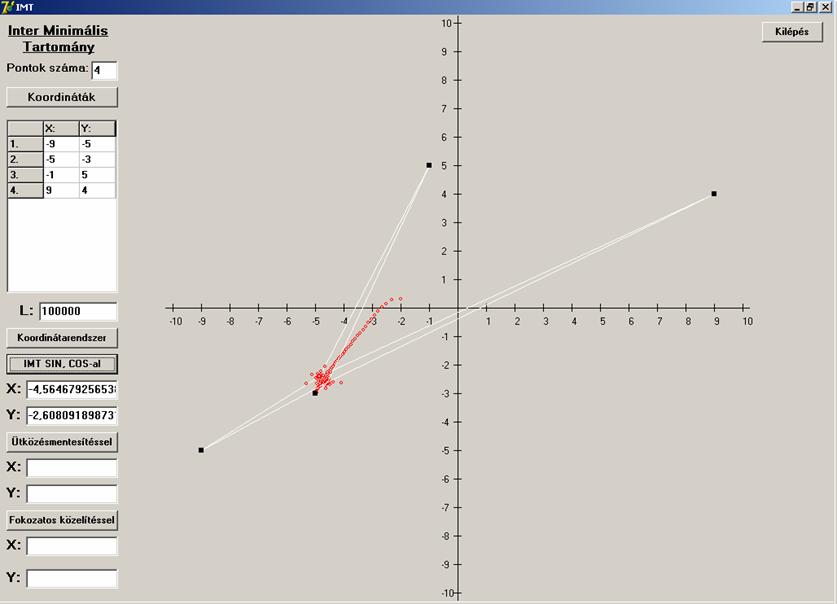
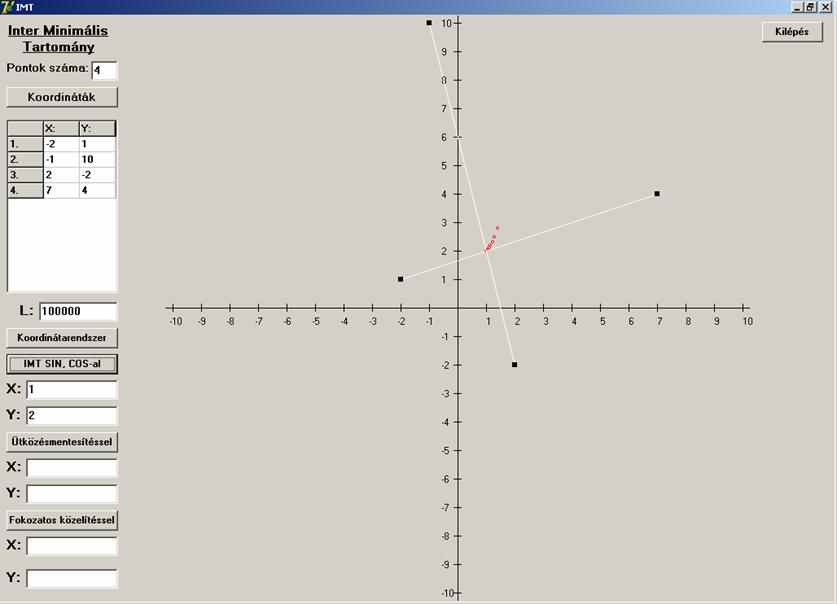
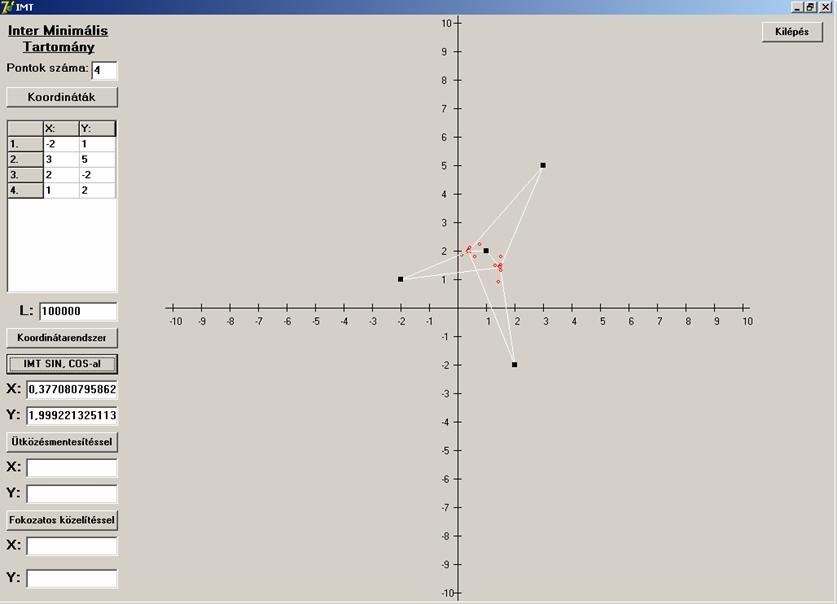
Most lássuk mi a helyzet a második algoritmussal.
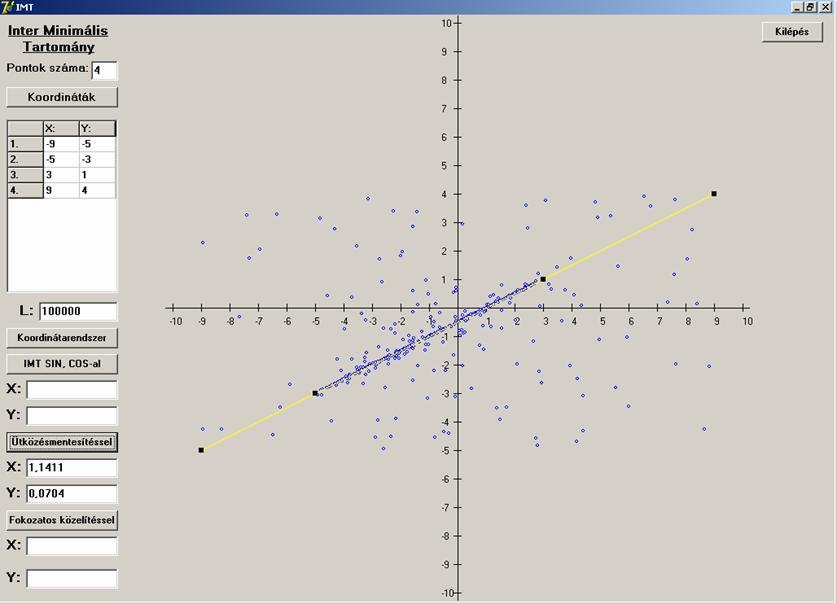
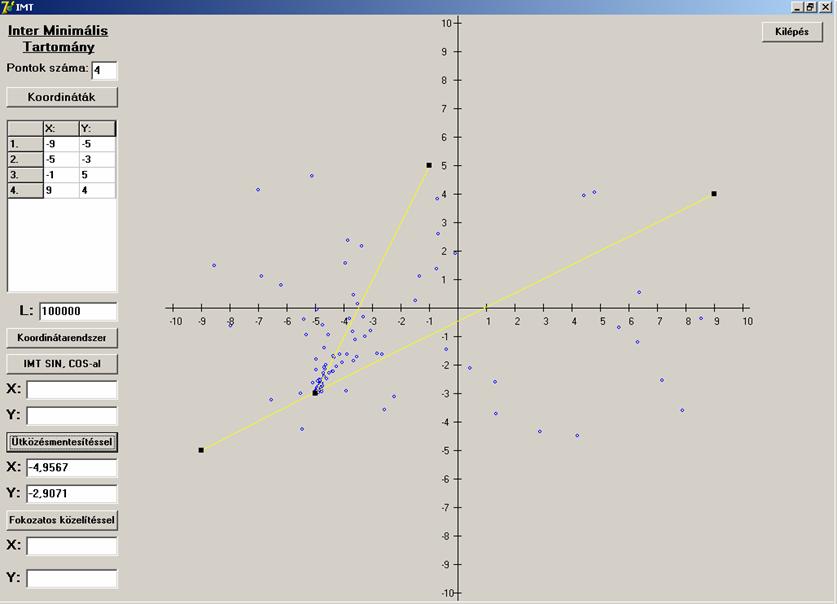
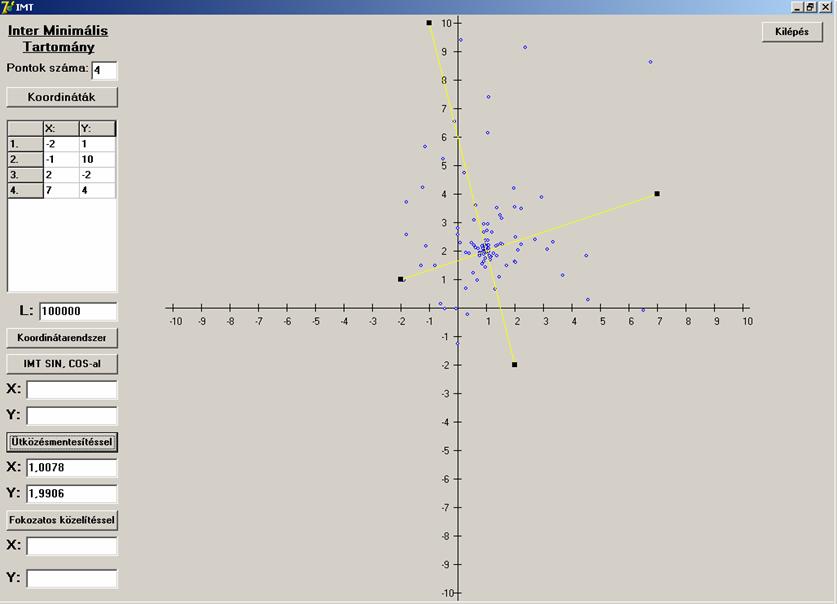
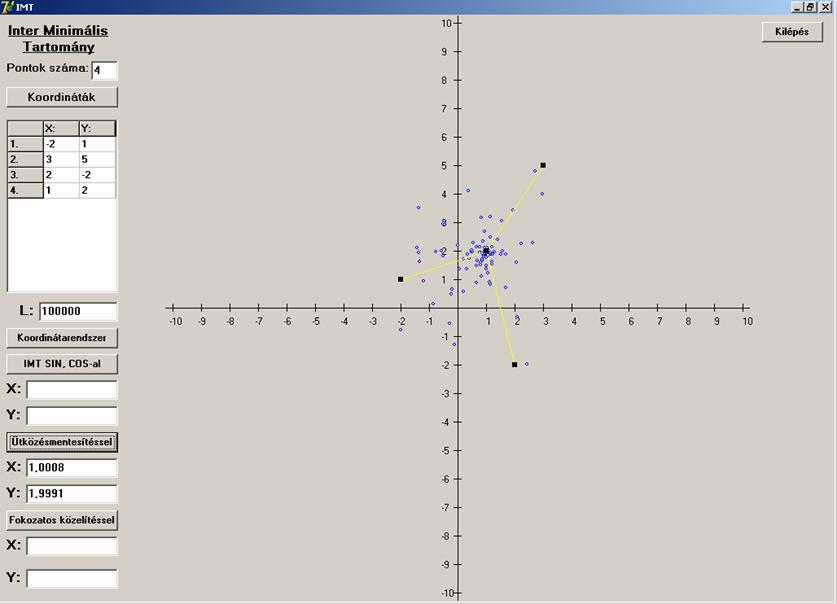
És végül a harmadik algoritmussal oldjuk meg az
előzőket.
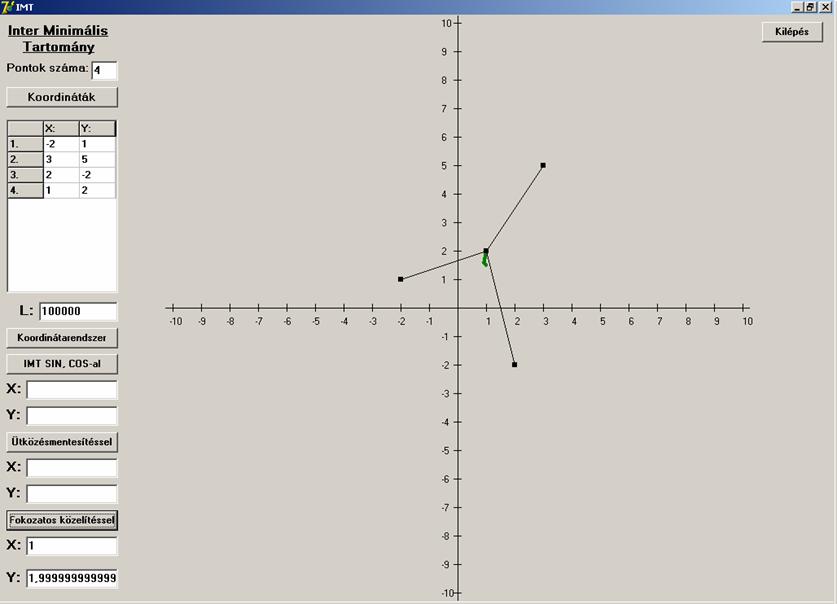
Négy pontra az algoritmusok ugyanúgy viselkedtek, mint
három pontra. Itt is az első a megbízhatatlan, a másik kettő mindig adott
megoldást. A második még azt is érzékeltette a keresési pontok által, hogy a
négy egy egyenesre eső pontok esetében a középső szakasz bármely pontja
megoldás lehet, hiszen itt sűrűsödtek be a keresési pontok.
Következő
lap: http://gorbem.hu/MT/Izogonalis3.htm