Háromszögek (6)

Vissza: http://gorbem.hu/Matematika.php

Szögfüggvények a derékszögű háromszögekben

A következő definíciókban, a derékszögű háromszögben a befogókat a-val és b-vel, az átfogót c-vel jelöljük (a velük szemközti szögeket pedig a szokásos módon). Nézzük, milyen összefüggés van a derékszögű háromszög oldalai és szögei között.

Egy derékszögű háromszögben a hegyesszöggel szemközti befogó és az átfogó hányadosát a szög szinuszának nevezzük. Jelölésben:

Egy derékszögű háromszögben a hegyesszög melletti befogó és az átfogó hányadosát a szög koszinuszának nevezzük. Jelölésben:

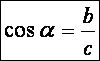
Egy derékszögű háromszögben a hegyesszöggel szemközti és a szög melletti befogó hányadosát a szög tangensének nevezzük. Jelölésben:

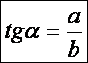
Egy derékszögű háromszögben a hegyesszög melletti és a szöggel szemközti befogó hányadosát a szög kotangensének nevezzük. Jelölésben:

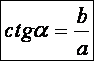
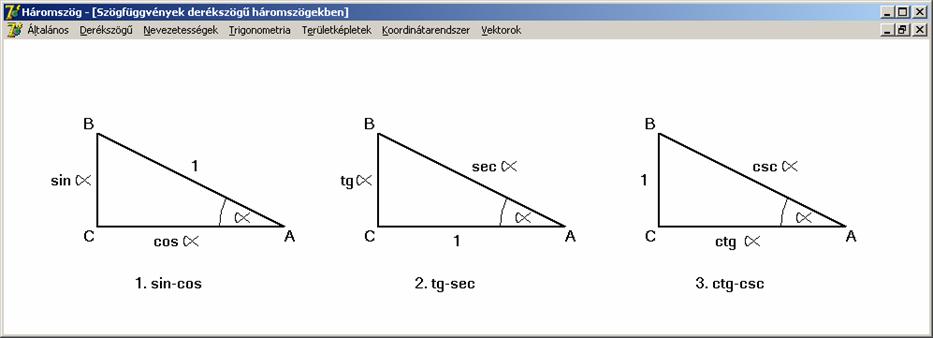
Egy derékszögű háromszögben az átfogó és a hegyesszög melletti befogó hányadosát a szög szekánsának nevezzük. Jelölésben:

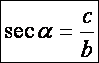
Egy derékszögű háromszögben az átfogó és a hegyesszöggel szemközti befogó hányadosát a szög koszekánsának nevezzük. Jelölésben:

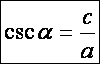
Ez utóbbi két szögfüggvényt (sec és csc) csak a teljesség kedvéért szokták megemlíteni, nagyon ritkán használjuk őket. Mivel az előző definíciókban az oldalak arányai szerepelnek, így valójában a szögfüggvények értéke nem az oldalaktól függ, hanem a hegyesszögektől. Ha ugyanis a derékszögű háromszögben megadunk egy hegyesszöget, akkor a háromszög minden szögét ismerjük. Ez a háromszögek hasonlóságának a negyedik alapesete, így az összes egymáshoz hasonló derékszögű háromszög megfelelő oldalainak aránya megegyezik, hányadosuk állandó, ami csak a hegyesszögtől függ, és egyenlő az aktuális szögfüggvény értékével.

A legfontosabb összefüggések ugyanazon szög különböző szögfüggvényei között, amelyek a definíciójukból adódik.

Ez utóbbit szokás trigonometrikus Pitagorasz tételnek is nevezni. A bizonyításban használjuk fel a Pitagorasz tételt, és a szögfüggvények derékszögű háromszögbeli definícióját.

Mindezt egy rajzon is megtekinthetjük:

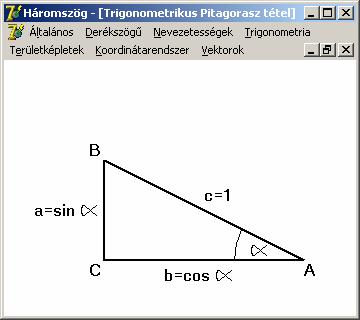
Ezek alapján készíthetünk egy olyan teljes táblázatot is, amelyből bármely szögfüggvénynek bármely másikkal való kifejezése kiolvasható:

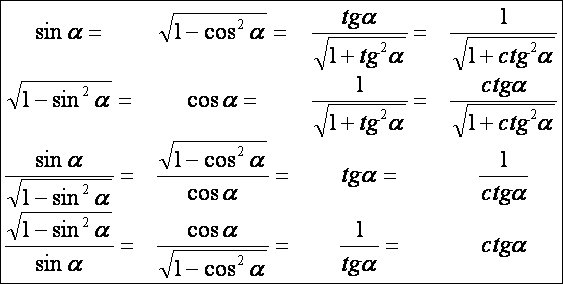
Pótszögek szögfüggvényei, melyek gyakorlatilag a derékszögű háromszög másik hegyesszögének, a β = (90º - α)-nak a szögfüggvényei:

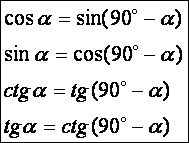
Szögfüggvények általánosítása

Mivel egy általános háromszögben előfordulhat 90º-os szögnél nagyobb szög is, célszerű a szögfüggvények általánosításával foglalkoznunk. Ehhez egy kis koordinátageometria szükséges. Helyezzünk a koordinátarendszer origójába egy egységvektort. Legyen az egységvektor kezdő helyzete (1,0), majd forgassuk körbe az óra járásával ellentétes irányban. Miközben körbefordul, a vektor két koordinátája a szinusz és koszinusz függvény értékeit szolgáltatja. A definíciók:

Egy tetszőleges szög szinusza alatt értjük a koordinátarendszerben hozzá tartozó egységvektor (irányszöge a kérdéses szög) y koordinátáját.

Egy tetszőleges szög koszinusza alatt értjük a koordinátarendszerben hozzá tartozó egységvektor (irányszöge a kérdéses szög) x koordinátáját.

Egy olyan szögnek, amelynek koszinusza nem nulla, a tangense alatt értjük szinuszának és koszinuszának a hányadosát.

Egy olyan szögnek, amelynek szinusza nem nulla, a kotangense alatt értjük koszinuszának és szinuszának a hányadosát.

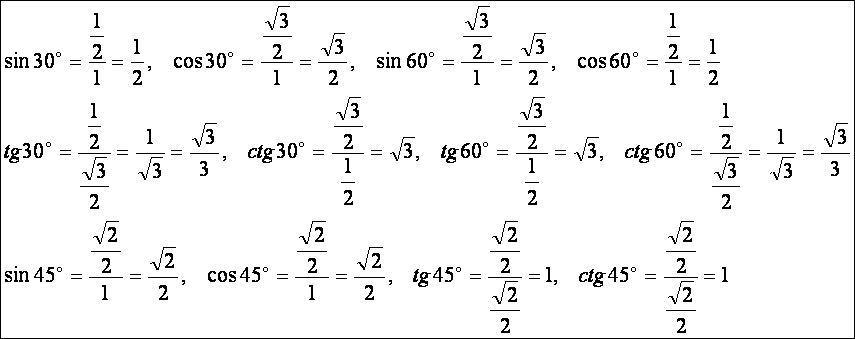
Nevezetes szögek szögfüggvényei:

Ezeket legegyszerűbben a következő derékszögű háromszögekről olvashatjuk le:

Az oldalak hossza nyilvánvalóan helyes, hiszen:

Azaz a Pitagorasz tétel megfordítása értelmében a háromszögek valóban derékszögűek. Nézzük a leolvasható szögfüggvényeket:

Mint azt fentebb említettem, a bevezetés módja ellenére, a szögfüggvény nem a derékszögű háromszögnek, hanem magának a szögnek a tulajdonsága, amint azt a szögfüggvény általánosításából is láthatjuk. Célszerű alaposabban megismerni ezeket a függvényeket, ezért ábrázoljuk őket.

Az y = sin(x) függvény tulajdonságai:

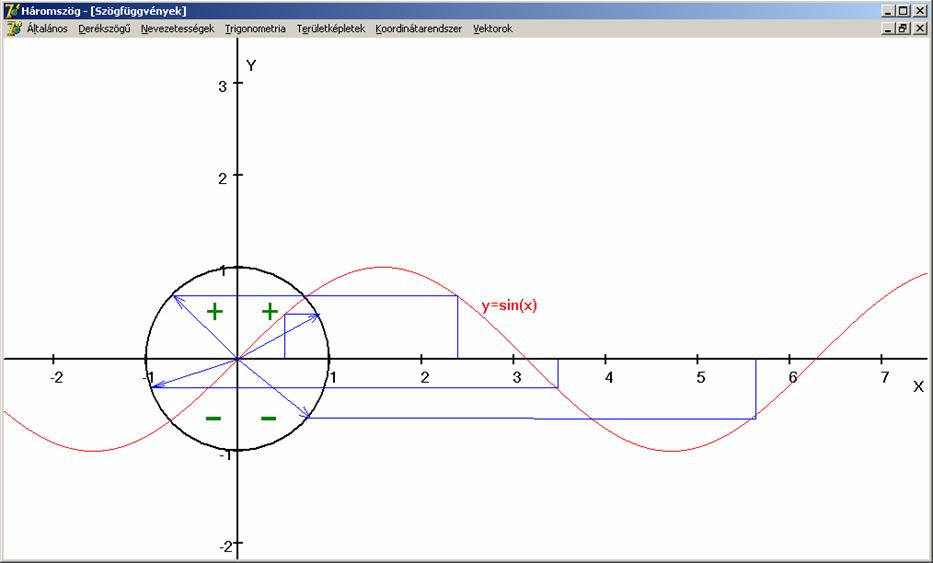
Értelmezési tartománya: (R: valós számok halmaza).

Értékkészlete: . Az első és második sík-negyedben pozitív, a harmadik és negyedikben negatív.

Helyi maximuma van az x = π/2 + 2kπ helyeken, melynek értéke 1.

Helyi minimuma van az x = 3π/2 + 2kπ helyeken, melynek értéke -1.

Zérus-helyei: x = kπ, ahol: (Z: egész számok halmaza).

A függvény 2π szerint periodikus. Fő-értékeit a [0, 2π] intervallumon veszi fel. (A szögletes zárójel zárt intervallumot jelöl.)

Szakaszosan monoton: [-π/2 + 2kπ, π/2 + 2kπ] intervallumon szigorúan monoton nő, [π/2 + 2kπ, 3π/2 + 2kπ] intervallumon szigorúan monoton csökken (ahol k: egész szám).

Konvexitás: [2kπ, π + 2kπ] intervallumon alulról konkáv (a grafikon az érintője alatt van), a [π + 2kπ, 2π + 2kπ] intervallumon (a grafikon az érintője felett van) alulról konvex (ahol k: egész szám).

Inflexió (konvexből konkávvá vált és viszont – az érintő egyben metszi is a függvénygörbét): az x = kπ, ahol: (Z: egész számok halmaza).

A szinusz függvény páratlan, azaz az origóra középpontosan szimmetrikus, vagyis sin(x) = -sin(-x). Ha a szinusz függvényt π-vel toljuk el balra, akkor a függvény negatívját kapjuk: sin(x) = -sin(x+ π).

A függvény folytonos és deriválható, deriváltja az y = cos(x) függvény.

Megemlíthetjük még azt, hogy a szinusz függvény írja le egy körpályán mozgó pontszerű test helyének y koordinátáját, ugyanúgy, mint a csillapítatlan harmonikus rezgőmozgást végző pontszerű test nyugalmi helyzetétől való kitérését is.

Az y = cos(x) függvény tulajdonságai:

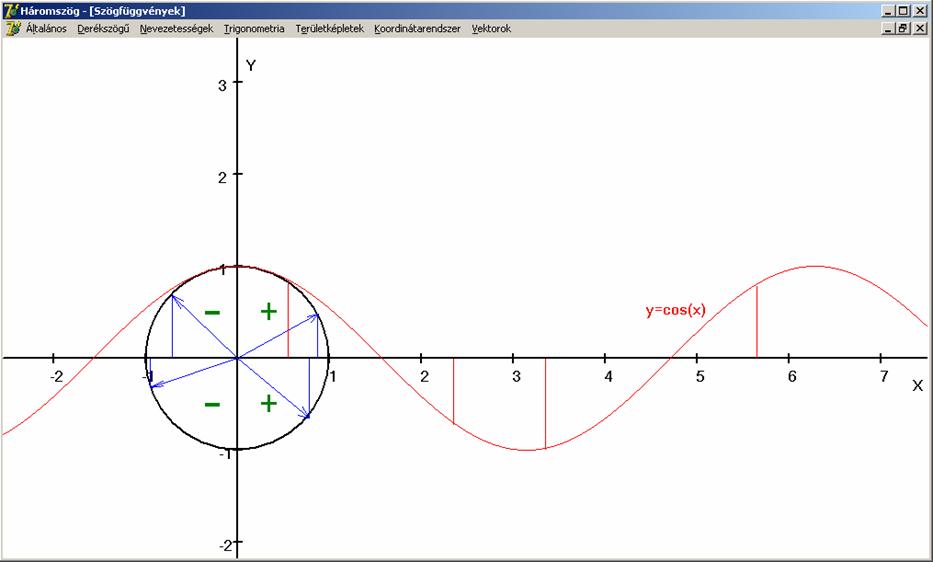
Értelmezési tartománya: (R: valós számok halmaza).

Értékkészlete: . Az első és negyedik sík-negyedben pozitív, a második és harmadik negatív.

Helyi maximuma van az x = 2kπ helyeken, melynek értéke 1.

Helyi minimuma van az x = π + 2kπ helyeken, melynek értéke -1.

Zérus-helyei: x = π/2 + kπ, ahol: (Z: egész számok halmaza).

A függvény 2π szerint periodikus. Fő-értékeit a [0, 2π] intervallumon veszi fel.

Szakaszosan monoton: [2kπ, π + 2kπ] intervallumon szigorúan monoton csökken, [π + 2kπ, 2π + 2kπ] intervallumon szigorúan monoton nő (ahol k: egész szám).

Konvexitás: [-π/2+2kπ, π/2 + 2kπ] intervallumon alulról konkáv (a grafikon az érintője alatt van), a [π/2 + 2kπ, 3π/2 + 2kπ] intervallumon (a grafikon az érintője felett van) alulról konvex (ahol k: egész szám).

Inflexió (konvexből konkávvá vált és viszont – az érintő egyben metszi is a függvénygörbét): az x = π/2 + kπ, ahol: (Z: egész számok halmaza).

A koszinusz függvény páros, azaz az y tengelyre szimmetrikus, vagyis: cos(x) = cos(-x). Ha a koszinusz függvényt π-vel toljuk el balra, akkor a függvény negatívját kapjuk: cos(x) = -cos(x+ π). Ha csak π/2-vel toljuk el, de jobbra, akkor a szinusz függvényt kapjuk: sin(x) = cos(x - π/2).

A függvény folytonos és deriválható, deriváltja az y = -sin(x) függvény.

Megemlítjük még, hogy a koszinusz függvény a szinusz függvény transzformáltja, melyet a szinusz függvénynek π/2-vel negatív irányba való eltolásával kapunk, azaz: cos(x) = sin(x+ π/2).

Az y = tg(x) függvény tulajdonságai:

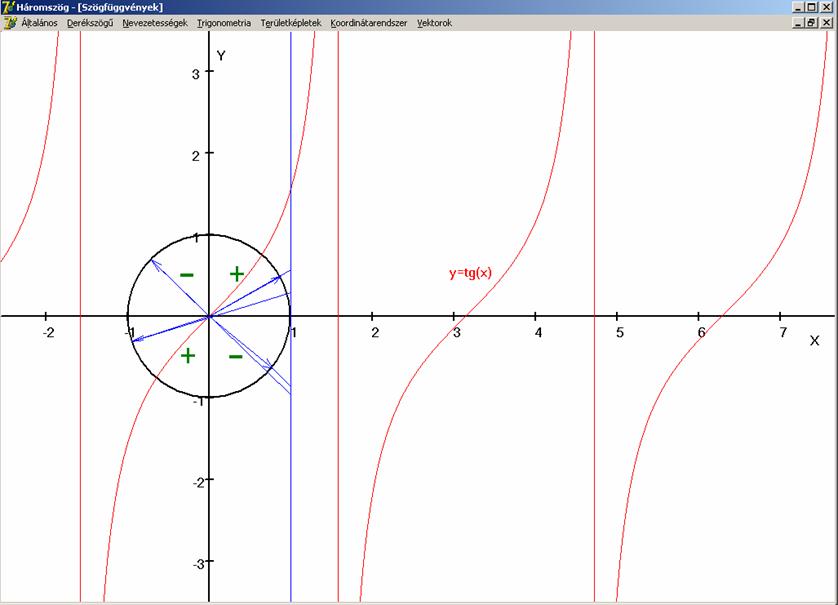
Értelmezési tartománya: (R: valós számok halmaza), kivéve a π/2 + kπ értékeket, ahol nem megszüntethető szakadása van.

Értékkészlete: . Az első és harmadik sík-negyedben pozitív, a második és negyedikben negatív.

Zérus-helyei: x = kπ, ahol: (Z: egész számok halmaza).

A függvény π szerint periodikus. Fő-értékeit a (-π/2, π/2) intervallumon veszi fel. (A gömbölyű zárójel nyílt intervallumot jelöl.)

Szakaszosan monoton: (-π/2 + kπ, π/2 + kπ) intervallumon szigorúan monoton nő (ahol k: egész szám).

Konvexitás: (-π/2+kπ, kπ) intervallumon alulról konkáv (a grafikon az érintője alatt van), a (kπ, π/2 + kπ) intervallumon (a grafikon az érintője felett van) alulról konvex (ahol k: egész szám).

Inflexió (konvexből konkávvá vált és viszont – az érintő egyben metszi is a függvénygörbét): az x = kπ, ahol: (Z: egész számok halmaza).

A függvény az értelmezési tartománya bármely pontjában folytonos, szakadási helyein nincs kétoldali határértéke, tágabb értelemben van baloldali határértéke ami ∞, és jobboldali ami -∞.

A tangens függvény páratlan, azaz az origóra középpontosan szimmetrikus, vagyis tg(x) = -tg(-x).

A tangens függvény deriválható, deriváltja az y = 1/cos²x függvény.

A tangens szó jelentése érintő. A szögfüggvény értékeit a fenti koordinátarendszerben, az origó középpontú, egységnyi sugarú kör (1,0) pontjába rajzolt érintőn leolvashatók, ha a forgó egységvektor egyenesének és az érintőnek a metszéspontját megkeressük és annak az y koordinátáját tekintjük.

Az y = ctg(x) függvény tulajdonságai:

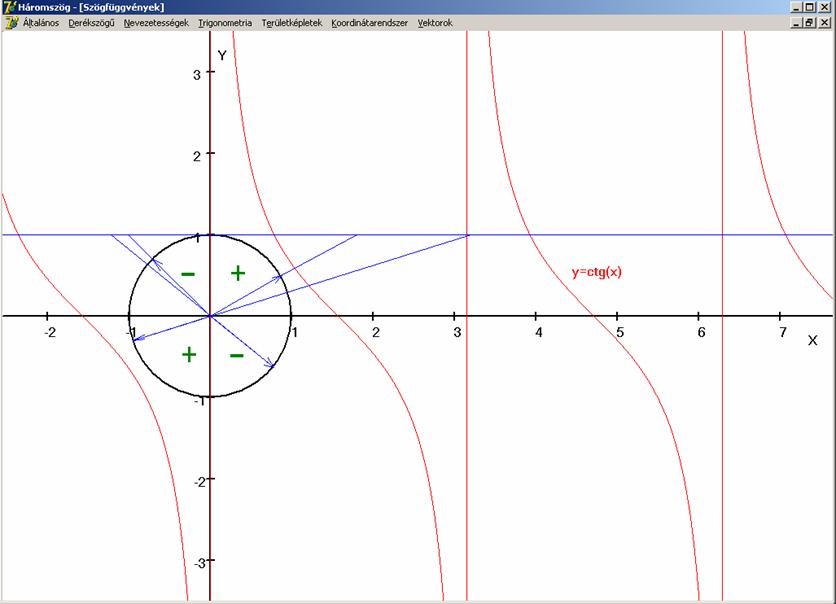
Értelmezési tartománya: (R: valós számok halmaza), kivéve a kπ értékeket, ahol nem megszüntethető szakadása van.

Értékkészlete: . Az első és harmadik sík-negyedben pozitív, a második és negyedikben negatív.

Zérus-helyei: x = π/2 + kπ, ahol: (Z: egész számok halmaza).

A függvény π szerint periodikus. Fő-értékeit a (0, π) intervallumon veszi fel.

Szakaszosan monoton: (kπ, π + kπ) intervallumon szigorúan monoton csökken (ahol k: egész szám).

Konvexitás: (π/2+kπ, π + kπ) intervallumon alulról konkáv (a grafikon az érintője alatt van), a (kπ, π/2 + kπ) intervallumon (a grafikon az érintője felett van) alulról konvex (ahol k: egész szám).

Inflexió (konvexből konkávvá vált és viszont – az érintő egyben metszi is a függvénygörbét): az x = π/2 + kπ, ahol: (Z: egész számok halmaza).

A függvény az értelmezési tartománya bármely pontjában folytonos, szakadási helyein nincs kétoldali határértéke, tágabb értelemben van baloldali határértéke ami -∞, és jobboldali ami ∞.

A kotangens függvény páratlan, azaz az origóra középpontosan szimmetrikus, vagyis: ctg(x) = -ctg(-x). A függvény a tangens függvénnyel így fejezhető ki: ctg(x) = -tg(x+π/2).

A kotangens függvény deriválható, deriváltja az y = -1/sin²x függvény.

A szögfüggvény értékeit a fenti koordinátarendszerben, az origó középpontú, egységnyi sugarú kör (0,1) pontjába rajzolt érintőn leolvashatók, ha a forgó egységvektor egyenesének és az érintőnek a metszéspontját megkeressük és annak az x koordinátáját tekintjük.

A trigonometrikus alapegyenletek megoldásai (az arc a trigonometrikus függvények inverzét jelöli):

sin(x) = a egyenlet megoldása: x₁ = 2kπ + arcsin(a), x₂ = (2k+1)π – arcsin(a).

cos(x) = b egyenlet megoldása: x₁ = 2kπ + arccos(b), x₂ = 2kπ – arccos(b).

tg(x) = c egyenlet megoldása: x = kπ + arctg(c).

ctg(x) = d egyenlet megoldása: x = kπ + arcctg(d).

Addiciós tételek, trigonometriai azonosságok:

Két szög összegének szögfüggvényei:

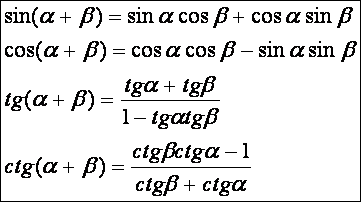
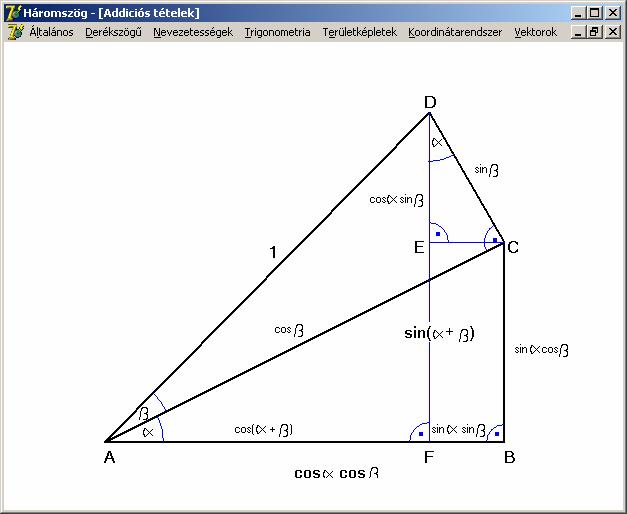
Az előző rajz segítségével a két szög összegének szinusza és koszinusza hegyesszögek esetére könnyen igazolható. A rajzon két egymás mellé illesztett derékszögű háromszöget látunk, melyek hegyesszögei α és β. Az ACD háromszög átfogója egységnyi. Ebből kiindulva a következők adódnak:

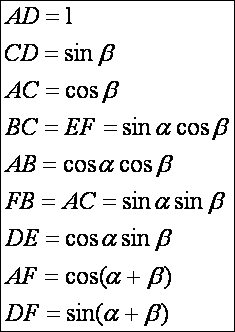
Mivel DF = EF +ED, ezért:

Mivel AF = AB – FB, ezért:

A két szög összegére vonatkozó első két (sin-ra és cos-ra vonatkozó) azonosságot hegyesszögre beláttuk. Könnyen megmutatható és ellenőrizhető, hogy ezek tetszőleges szögekre érvényesek.

Most lássunk egy bizonyítást területek segítségével.

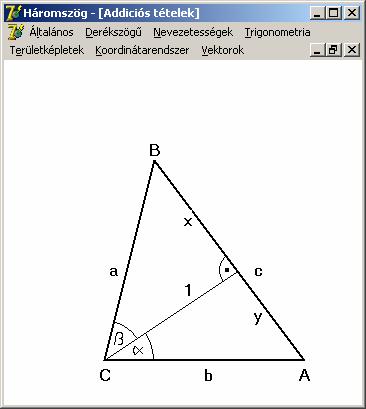
Az ABC háromszög területét kétféleképpen is felírhatjuk:

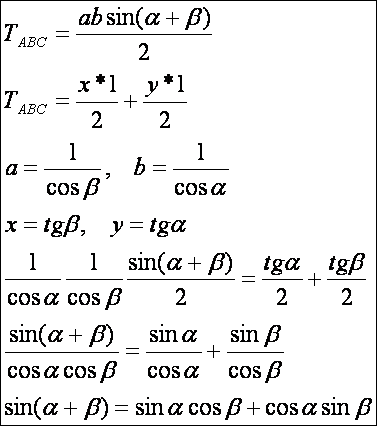
A következő bizonyításban nem használjuk fel azt, hogy a szögek hegyesszögek. A következő ábrán minden vektor egységvektor. Az i’ és j’ az i és j α szöggel való elforgatottja, így egymásra merőlegesek ugyanúgy, mint az i és j voltak. Az i’-t tovább forgatjuk pozitív irányba β szöggel, így kapjuk az e vektort.

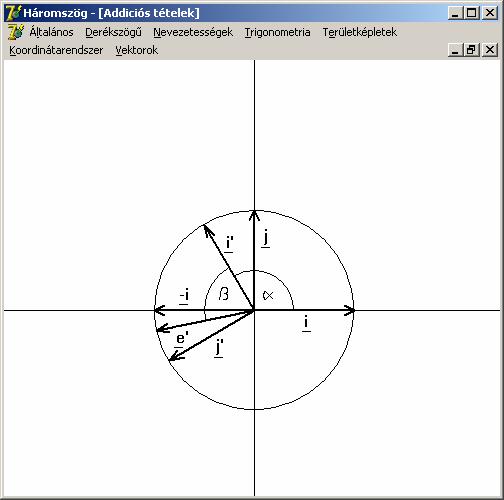
Ezek alapján:

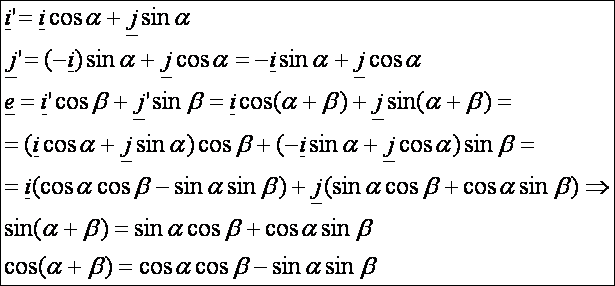
A tangens és kotangensre vonatkozó azonosságokat már ezek felhasználásával igazolhatjuk:

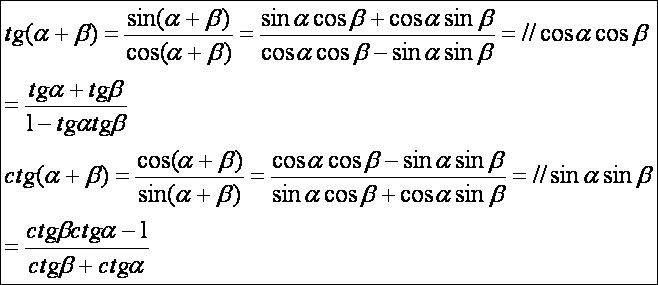
Két szög különbségének szögfüggvényei:

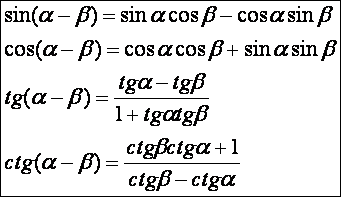
Ezeket az azonosságokat úgy bizonyíthatjuk, hogy β helyébe (-β)-t, és ennek következtében cos(-β) = cos β-t és sin(-β) = -sin β-t írunk.

Két szögfüggvény összegének szorzattá alakítása:

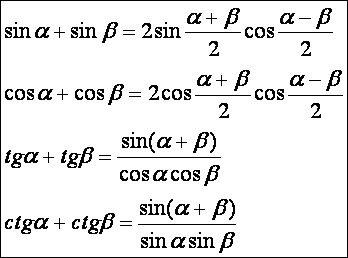
Lássuk az elsőnek a bizonyítását:

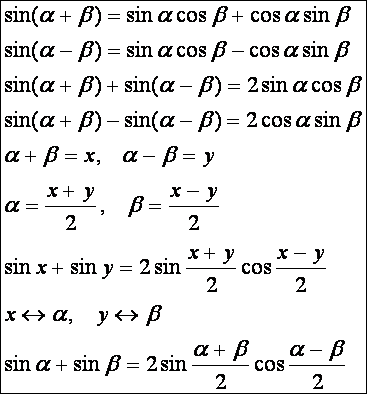
Két szögfüggvény különbségének szorzattá alakítása:

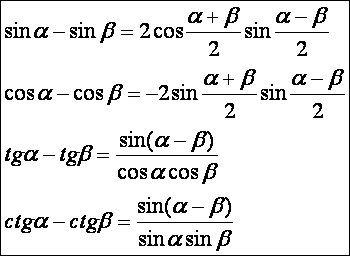
Kétszeres szögek szögfüggvényei:

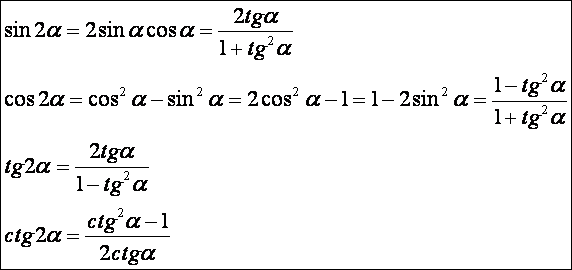
Ezeknek a bizonyításánál egyszerűen a két szög összegére vonatkozó formulában a β helyett is α-t írunk, például a szinusz esetén:

Fél-szögek szögfüggvényei:

Bizonyítás:

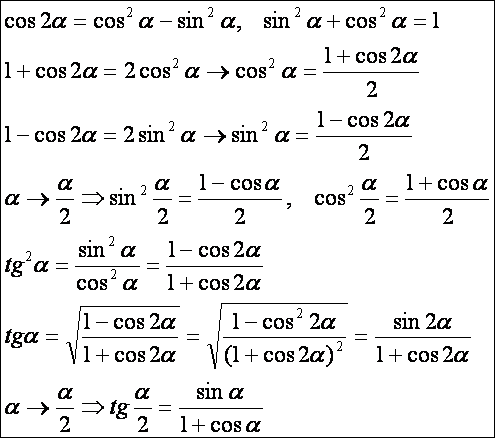
Háromszoros szögek szögfüggvényeinek levezetése:

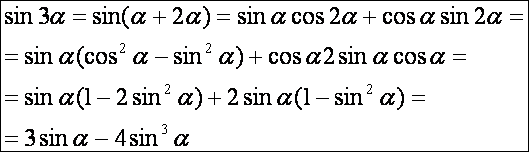
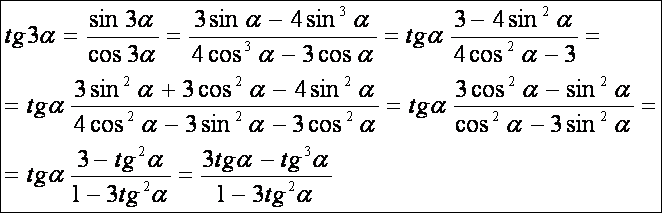
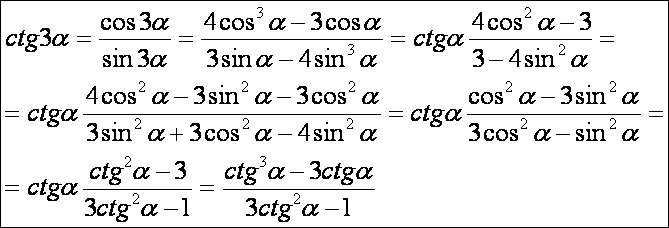
Szög szinuszának kifejezése tg(α/2) segítségével:

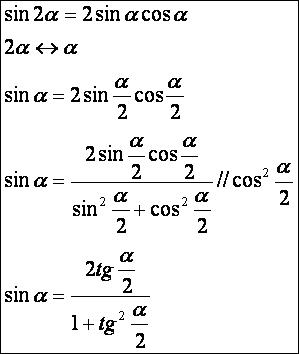
Szög koszinuszának kifejezése tg(α/2) segítségével:

A háromszög trigonometriája

A továbbiakban áttérünk a háromszögekben érvényes tételekre, azaz a következő állításokban a szakaszok és szögek egy háromszög alkotóelemei.

Szinusz tétel.

Egy háromszögben az oldalak úgy aránylanak egymáshoz, mint a velük szemben lévő szögeinek szinuszai.

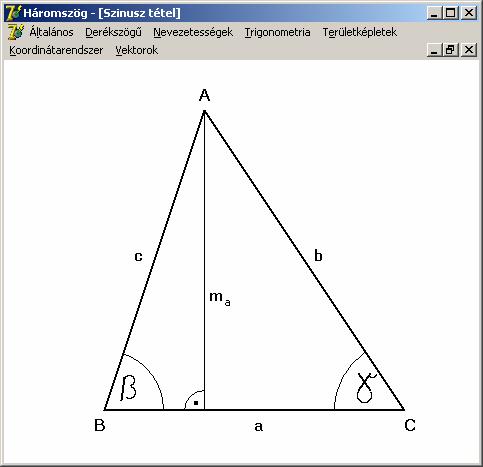
A bizonyításhoz használjuk az előző rajz jelöléseit. Írjuk fel az a oldalhoz tartozó magasságot az a oldalon lévő két szög és a másik két oldal segítségével.

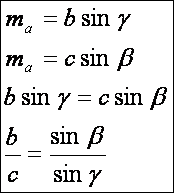
Hasonlóan a további oldalakra:

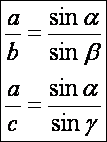
A szinusz tételnek egy még többet eláruló alakja:

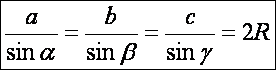
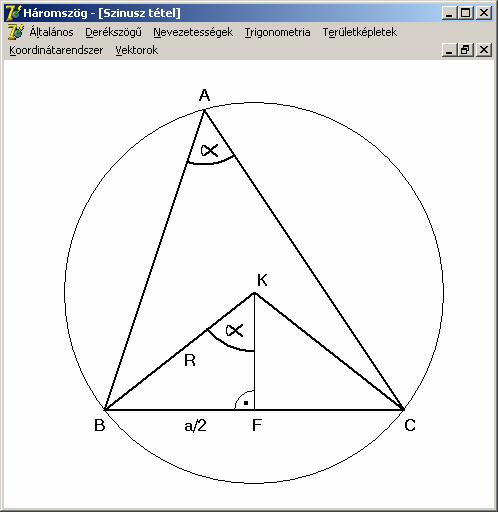
Ennek bizonyításhoz tekintsük az előző rajzot, ahol K a köré írható kör középpontja. Használjuk fel a kerületi és középponti szögek tételét és írjuk fel az α szög szinuszát a BFK derékszögű háromszögben:

Hasonlóan a másik két oldalra:

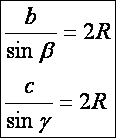
Amiből a tétel állítása már nyilvánvaló.

Koszinusz tétel.

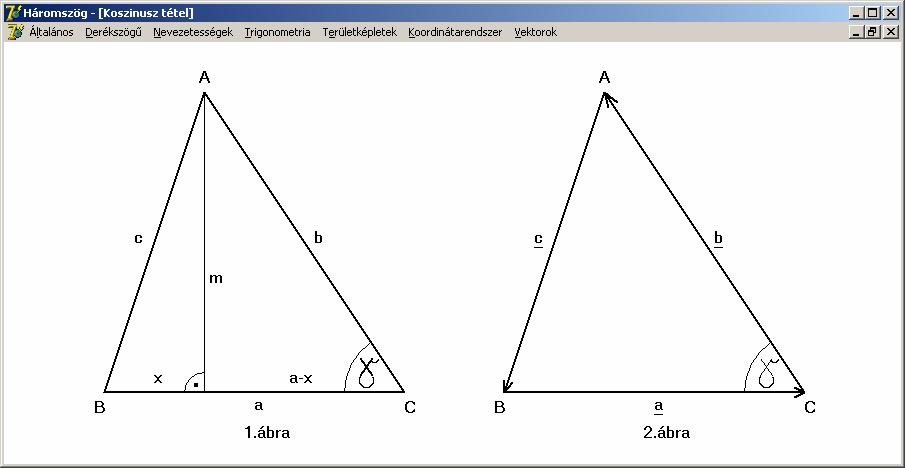
Tekintsük az előző rajz első ábráját. Írjunk fel az a oldalhoz tartozó magasságra két Pitagorasz tételt, majd küszöböljük ki az egyenletekből a magasságot:

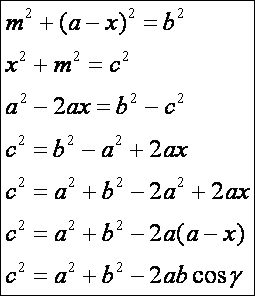
Ez utóbbi pedig nem más, mint koszinusz tétel.

Bizonyítás vektorok segítségével. Irányítsuk a háromszög oldalait úgy, hogy a keletkező három vektor összege null-vektor legyen, úgy ahogyan azt az előző rajz 2. ábráján láthatjuk. Majd rendezzük és emeljük négyzetre (skaláris szorzással) az egyenlet mindkét oldalát, így kapjuk a koszinusz tételt:

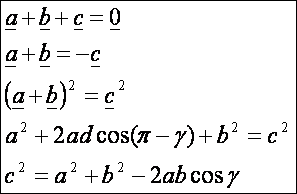
Pitagorasz tétele, mint a koszinusz tétel speciális esete. Alkalmazzuk a koszinusz tételt derékszögű háromszögre.

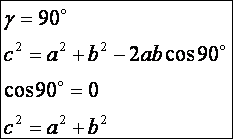
Tangens tétel.

Bármely háromszögben igaz a következő összefüggés, melyet tangens-tételként ismerhetünk:

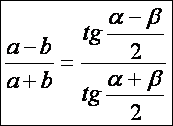
A tétel bizonyítása a szinusz tétel segítségével (2R = d a háromszög köré írható kör átmérője):

A háromszögekben a következő fél-szögképletek érvényesek (s természetesen a fél-kerület):

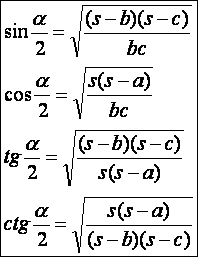
Tangensnégyzet-tétel:

Minden háromszögben érvényes a következő összefüggés:

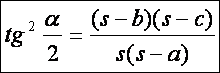
A tétel bizonyítása a fél-szögképletek segítségével:

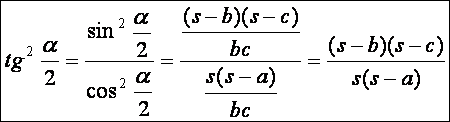
Következő lap: http://gorbem.hu/MT/Haromszog7.htm