Háromszögek (4)

Vissza: http://gorbem.hu/Matematika.php

Szabályos háromszögek

A szabályos háromszög a legegyszerűbb sokszög, abban az értelemben, hogy oldalszáma a lehető legkisebb, és alkotó elemei egymással egyenlők, így egyetlen adattal, például oldalának hosszával megadható. (A négyzet is hasonlóan egyszerű és talán alkotó elemei még könnyebben is számolhatók, de oldalainak száma miatt szerintem, lemarad az első helyről.) De inkább térjünk rá az objektívebb dolgokra. Tehát a szabályos háromszög oldalai és ebből következően a szögei is egyenlők. Mivel a háromszög szögeinek összege 180º, a szabályos háromszög minden szöge 60º-os. Tekintsük a következő rajzot. Megrajzoltuk a háromszög két szögfelezőjét: BF_b és CF_c szakaszokat. Legyen ezek metszéspontja O. Ekkor OF_c = OF_a és OF_a = OF_b, mivel a szögfelezőn azok a pontok találhatók, amelyek egyenlő távol vannak a szög száraitól. Ebből viszont az adódik, hogy OF_b = OF_a, azaz a harmadik szögfelező is átmegy az O ponton. Ez a pont a háromszögbe írható kör középpontja. A három szögfelező a szabályos háromszöget derékszögű háromszögekre bontja. Például az ABF_b derékszögű, mert az A csúcsnál 60 fokos a B csúcsnál 30 fokos szöge van, amiből adódik, hogy F_b-nél lévő szög 90 fokos. Ez mindegyik oldallal kapcsolatban elmondható. Mivel ezeknek a derékszögű háromszögeknek a az átfogója, így egybevágók. Ugyanez mondható el a kisebb, az AF_cO, BF_cO, … derékszögű háromszögekről is. Összegezve az eddigieket: tehát a megrajzolt szögfelezők metszéspontja a beírható kör középpontja. Mivel felezik a szemközti oldalt, ezért súlyvonalak is, metszéspontjuk tehát a háromszög súlypontja. Sőt, mivel merőlegesen felezik az oldalakat a metszéspontjuk a háromszög köré írható kör középpontja, a merőlegesség miatt pedig egyúttal magasságok is. Így az O pontra jogosan mondhatjuk, hogy a háromszög középpontja: O = K = S = M, ahol K: körülírható kör középpontja, S: súlypont, M: magasságpont. Továbbá egyenlő hosszúak a szögfelezőknek a háromszögbe eső szakaszai, a súlyvonalak hossza és a magasságok hossza: f = s = m. A háromszögnek minden szögfelezője a háromszög szimmetriatengelye. Ha pedig az O pont körül 120 fokkal elforgatjuk, akkor önmagába megy át.

Térjünk rá a szabályos háromszög adataira. A számításokhoz a Pitagorasz tételt használjuk:

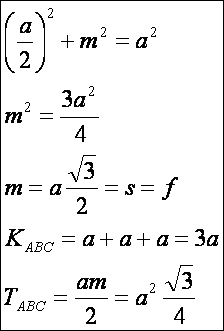
Jelölje r a beírható kör, R a köré írható kör, és az r_A = T/(s-a) a hozzáírt kör sugarát (kiszámítási módját lásd a lap végén):

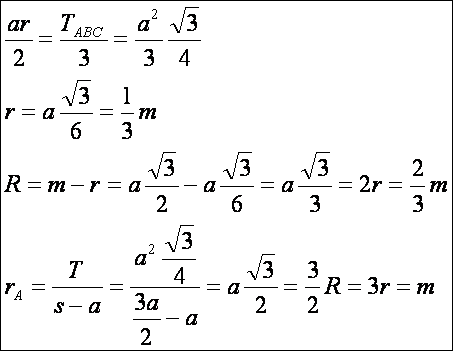
A szabályos háromszögekkel kapcsolatban két szélsőértéket kell megemlíteni. Az azonos kerületű háromszögek közül a szabályosnak a területe a legnagyobb. Illetve, az azonos területű háromszögek közül a szabályosnak a kerülete a legkisebb.

Egyenlőszárú háromszögek

Az egyenlő szárú háromszögnek van két egyenlő oldala, melyeket száraknak, az általuk bezárt szöget szárszögnek, a harmadik oldalt pedig alapnak nevezzük. Az egyenlő szárú háromszög alapjain fekvő szögek (mivel egyenlő oldalakkal vannak szemben) egyenlők. A szárszögének nagysága szerint lehet hegyes-, derék- és tompaszögű. Az alapon fekvő szögek aszerint kisebbek 45 foknál, egyenlők 45 fokkal vagy nagyobbak 45 foknál, amint az egyenlő szárú háromszög tompa-, derék- vagy hegyesszögű. A szárszög szögfelezője egyúttal az alaphoz tartozó súlyvonal, magasságvonal és oldalfelező merőleges és szimmetriatengely is. Emiatt az egyenlőszárú háromszög beírható körének O középpontja és az S súlypontja a szögfelezőnek a háromszögbe eső szakaszán található. A köré írható kör K középpontja és az M magasságpont a szögfelező egyenesén található, hegyesszögű háromszög esetén a háromszög belsejében, derékszögű esetén a háromszög kerületén, tompaszögű esetén a háromszögön kívül (a magasságpont a szárszög csúcsszögének a szögtartományában, a köré írható kör középpontja pedig a szögfelezőnek az alapon túlnyúló meghosszabbításán).

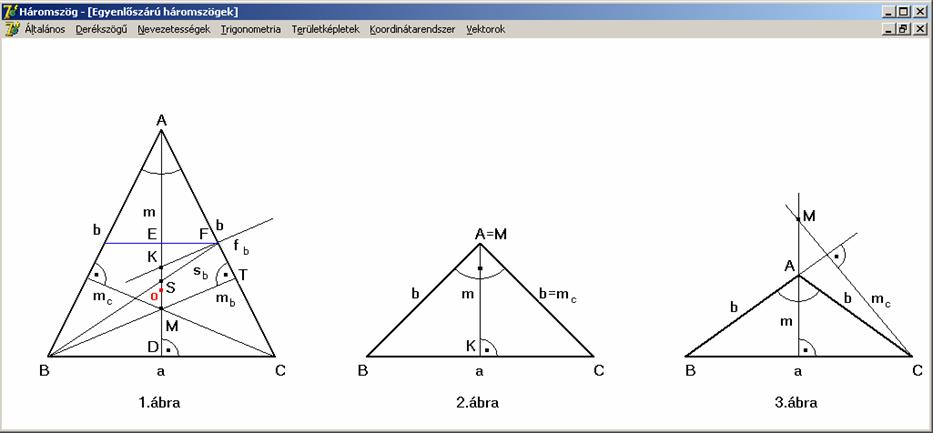
Az alábbi rajzon hegyes- (1. ábra), derék- (2. ábra) és tompaszögű (3. ábra) egyenlőszárú háromszögeket láthatunk. A háromszögeknek a az alapja, b a szára, m pedig a magassága. A magasság és a terület kiszámításához használjuk a Pitagorasz tételt:

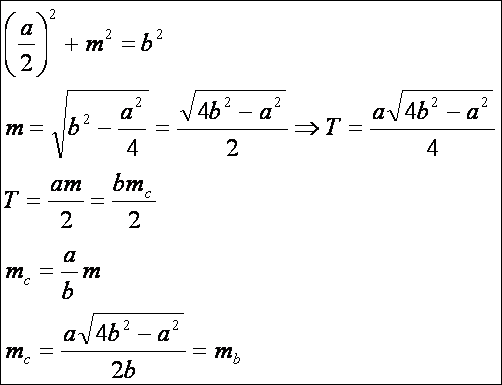
Az 1. ábra jelöléseit használva, számítsuk ki a hegyesszögű egyenlőszárú háromszög súlyvonalát (az s_a = m, így csak az s_b = s_c-t kell meghatározni).

Ugyancsak az 1. ábra jelöléseit használva, a BMS és SKF háromszögek hasonlók, hiszen oldalaik párhuzamosak illetve egy egyenesen helyezkednek el. Mivel az S a BF szakasz harmadoló pontja, így a hasonlóság aránya 1:2. Vagyis a KS és SM aránya is ugyanez, azaz az S a KM szakasznak a K-hoz közelebbi harmadoló pontja.

Számítsuk ki a KM szakasz hosszát. Jelölje KF = x, KE = y. Mivel a BDM és FEK háromszögek hasonlók és a hasonlóság aránya 1:2, így MB = 2x és KD = 2y. Ezek segítségével a KM = m/2 - 3y. A Pitagorasz tételt és az AEF és ABD háromszögek hasonlóságát felhasználva:

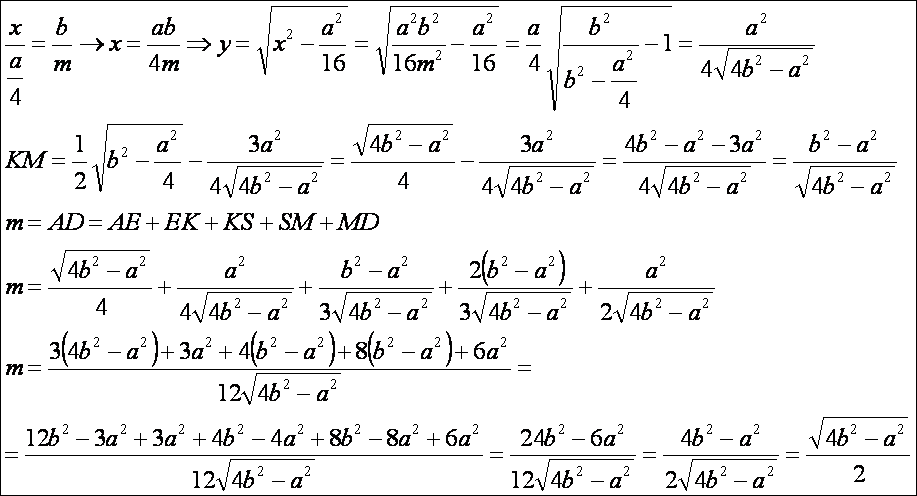
(Az m utóbbi, összegként való felírása csak a számolás helyességét igazolja.) Az AK szakasz hossza a köré írható kör sugara, amit jelöljünk a szokásos módon R-rel. Mivel AK = AE + EK = R = m/2 + y, így:

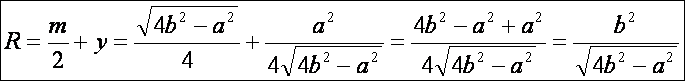
Számítsuk ki a háromszögbe írt kör r = OD sugarát a T = rs képlet segítségével:

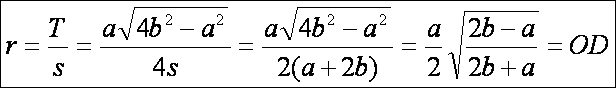
Nézzük a hozzáírt körök sugarát:

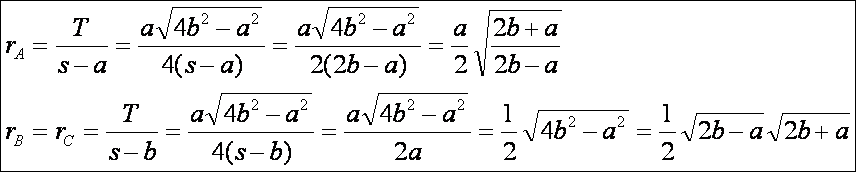
Már csak a KO = KD - OD meghatározása van hátra:

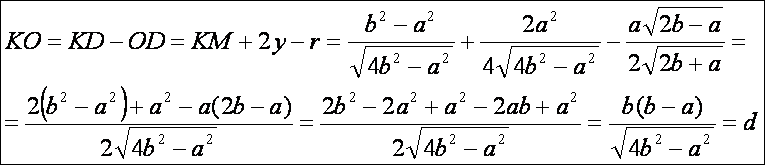
A későbbiekben láthatjuk, hogy az általános háromszögre érvényes az Euler-tétel, amely képletben: d² = R² - 2Rr, ahol d = KO, azaz a két kör középpontjának távolsága. Nézzük meg teljesül-e ez a meghatározott sugarakra és KO távolságra:

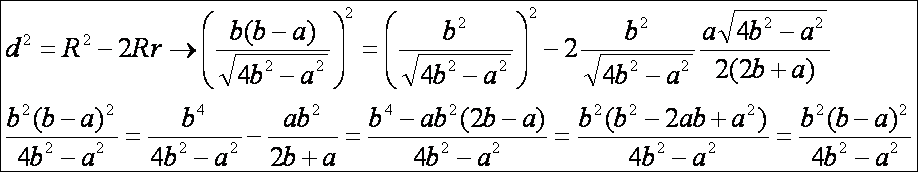
Természetesen igen, hiszen az R, r és KO kiszámítása helyesen történt, így az ellenőrző számítás nem talált hibát.

Egyenlő szárú derékszögű háromszög esetén a magasság és a terület:

A háromszögek nevezetes egyenesei, pontjai és körei

A háromszögek oldalfelező merőlegesei és a háromszög köré írható kör középpontja.

A háromszögben a három oldalfelező merőleges egy pontban metszi egymást. Ez a pont a háromszög köré írható kör középpontja, melyet K-val, a kör sugarát pedig R-rel jelöljük.

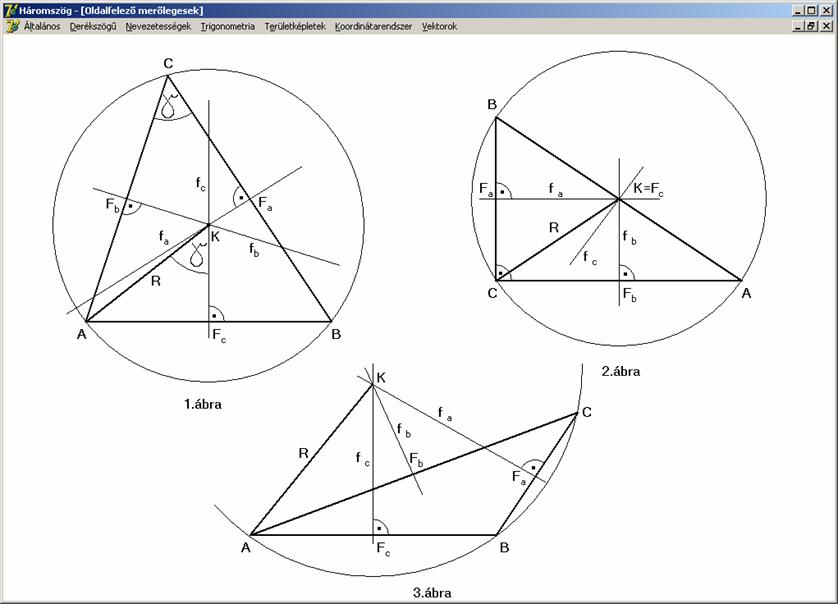
A bizonyításban azt látjuk be, hogy két oldalfelező metszéspontja rajta van a harmadik oldalfelező merőlegesen. A szakaszfelező tulajdonsága, hogy rajta olyan pontok vannak, amelyek egyenlő távol vannak a szakasz két végpontjától. Tekintsük az f_a és f_b oldalfelező merőlegeseket, melyek nyilvánvalóan metszik egymást, mert az ACB szög nem lehet 180º. Az f_a-n olyan pontok vannak, melyek egyenlő távol vannak a B és C csúcsoktól, például ilyen a metszéspontjuk K is, azaz KB = KC. A f_b-n olyan pontok vannak, amelyek egyenlő távol vannak az A és C csúcsoktól, így K-ra KA = KC is igaz. De ebből KA = KB adódik, azaz a K rajta van az f_c-n is, vagyis mindhárom oldalfelező merőlegesen. Tehát a Három oldalfelező merőlegesnek a K közös pontja. Mivel a K mindhárom csúcstól egyenlő távolságra van, így a háromszög köré írható kör középpontja (a három csúcspont egyértelműen meghatároz egy kört), melynek sugarát R-rel jelöljük. Az 1. ábra alapján a γ-val jelölt szögek a kerületi és középponti szögek tétele miatt egyenlők. Ennek alapján az R a háromszög oldalaival és a háromszög T területével így számolható ki:

Nézzük meg, hogyan függ a K helye a háromszög típusától. Az 1. ábrán egy hegyesszögű háromszög látható. Ekkor a K a háromszög belsejében van. A 2. ábra derékszögű háromszöget tartalmaz. A köré írható kör középpontja az átfogó felezőpontjában található K = F_c. A kör sugara az átfogó fele: R = c/2. A 3. ábrán pedig tompaszögű háromszöget láthatunk. Ekkor a K a háromszögön kívül, a tompaszög szögtartományában foglal helyet.

A háromszög belső szögfelezői és a háromszög beírható körének középpontja.

A háromszögben a belső szögek szögfelezői egy pontban metszik egymást. Ez a pont a háromszögbe írható kör középpontja, melyet a következő rajzon O-val jelöltünk (mely pont triviális módon, mindig a háromszög belsejében található). A beírható kör sugara r, melyet így számolhatunk ki: r = T/s (ahol T a háromszög területe, s pedig a fél-kerület). Az a, b, c oldalú háromszögbe írt kör érintési pontjai az oldalakat páronként s - a, s - b, s - c hosszúságú darabokra bontják.

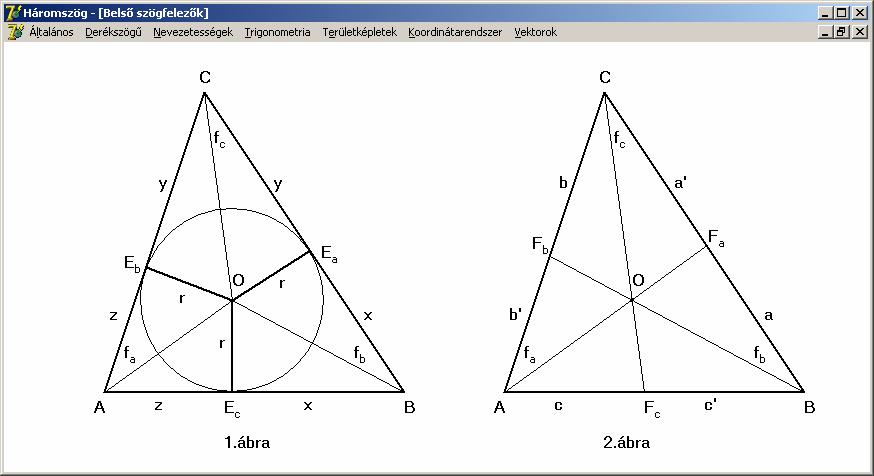
Annak a bizonyítása, hogy a belső szögfelezők egy ponton haladnak át, teljesen analóg az oldalfelezőknél alkalmazott bizonyítással. Vagyis belátjuk, hogy két szögfelező metszéspontja rajta van a harmadik szögfelezőn. A jobb áttekinthetőség miatt két ábrát fogunk használni. Tekintsük tehát az előző rajz 1. ábráját. A szögfelező tulajdonsága, hogy pontjai egyenlő távol vannak a szög száraitól. Így például az OE_a = OE_b és OE_b = OE_c mivel az O rajta van az f_c és az f_a szögfelezőn. De ebből OE_a = OE_c adódik, vagyis az O rajta van f_b-n, azaz a belső szögfelezők egy ponton mennek át.

Ha felírjuk a háromszög területét a beírható kör sugara segítségével, akkor a beírható kör sugarára a következőt kapjuk:

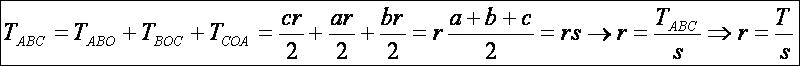
Bizonyítsuk be az állítást a Ceva tétel alapján is. A Ceva tétel megfordítása szerint, ha a Ceva-féle szakaszok a háromszög oldalaiból olyan metszeteket hoznak létre, hogy abc = a’b’c’, akkor a Ceva-féle szakaszok egy ponton mennek át. A bizonyításhoz felhasználjuk a szögfelező tételt (a tétel bizonyítását a Haromszog2.htm lapon láthatjuk), vagyis azt, hogy a szögfelező a szemközti oldalt a szomszédos oldalak arányában osztja. Azonosítások a fenti rajz 2. ábrája szerinti:

Ez utóbbi viszont a Ceva-féle tétel megfordítása szerint azt jelenti, hogy a három belső szögfelező egy ponton megy keresztül. Most térjünk át az érintő szakaszokra. Tekintsük újra az előző rajz 1. ábráját.

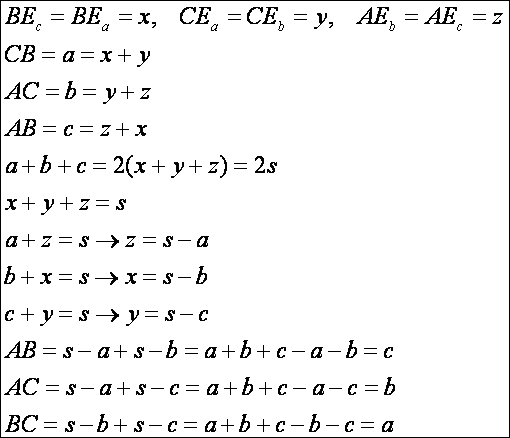
Euler-féle képlet és egyenlőtlenség.

Egy háromszög beírható köre középpontjának és a köré írható köre középpontjának d távolságát az Euler-féle képlet adja meg (r a beírható kör sugara, R a köré írható kör sugara):

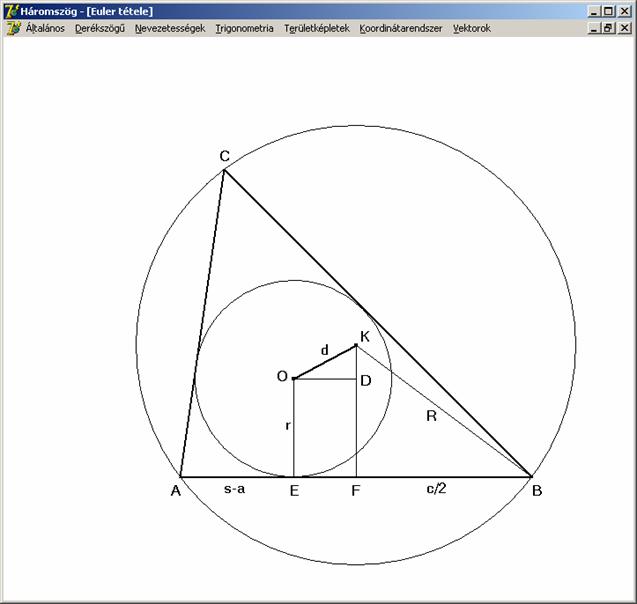
Használjuk az alábbi rajz jelöléseit. A d = OK szakasz az ODK derékszögű háromszög átfogója. (Megjegyezzük, hogy ha a háromszög nem szabályos, mindig választható olyan oldal, hogy az ODK háromszög az alábbi módon létezzen.) Határozzuk meg ennek a háromszögnek a befogóit:

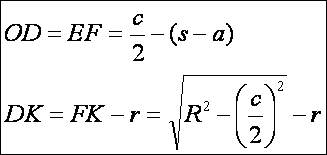
Írjuk fel az ODK derékszögű háromszögre a Pitagorasz tételt:

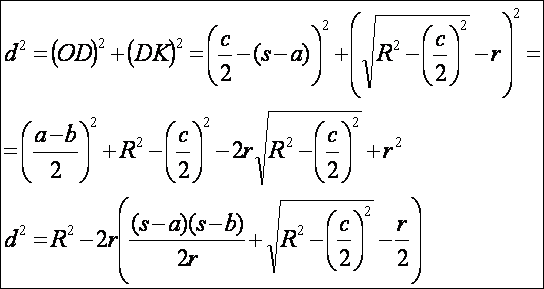
Ha az utóbbi összefüggést összevetjük az Euler-féle képlettel, akkor a következőnek kell igaznak lenni:

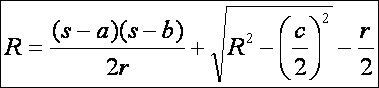
Próbálkozzunk meg ekvivalens átalakításokkal ezt igazolni:

Mivel a négyzetre emelés pozitív értékeken történt, így hamis gyök nem léphetett fel, az egyenletek ekvivalensek. Az átalakítások közben a következő helyettesítéseket alkalmaztuk:

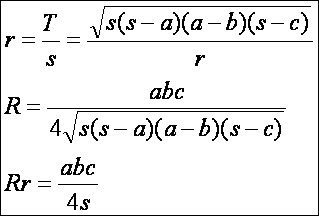
Mivel az átalakítások révén azonossághoz jutottunk, így az R valóban a fentebbi értékkel megegyezik, azaz az Euler-féle képlet tehát érvényes.

Az Euler-féle képletből egyszerűen adódik, hogy egy háromszög köré írható kör sugara mindig nagyobb vagy egyenlő, mint a beírható kör sugarának a kétszerese (Euler-féle sugáregyenlőtlenség), hiszen:

Az egyenlőtlenség második bizonyításában használjuk a későbbiekben tárgyalandó Heron-képletet, mely a háromszög területét adja meg az oldalak segítségével. Használjuk az r és R fentebb bebizonyított kiszámítási képletét, és az s-a, s-b és s-c szakaszokról térjünk át az előzőekben használt x, y és z szakaszokra (előző rajz 1. és 3. ábra):

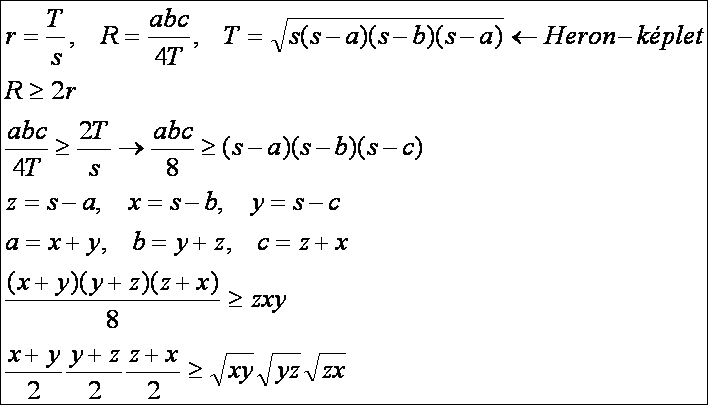
Ez utóbbi viszont a számtani és mértani közepek között fennálló egyenlőtlenség miatt igaz (három egyenlőtlenség megfelelő oldalainak az összeszorzásával kaphatjuk ezt az egyenlőtlenséget).

Középvonalak.

A háromszög bármely két oldalának felezőpontját összekötő szakasz, azaz a középvonal, párhuzamos a harmadik oldallal és fele olyan hosszúságú. Ez az állítás nyilvánvalóan igaz a párhuzamos szelőszakaszok tétele és megfordítása miatt.

A következő rajzon az F_aF_b, F_bF_c és FcF_a a középvonalak. A középvonalak által alkotott háromszöget a háromszög középponti vagy súlyponti háromszögének nevezzük. A középvonalakból álló háromszög és az eredeti háromszög egymáshoz párhuzamosan hasonló, a hasonlóság aránya 1:2. A középvonalak az eredeti háromszöget négy, egymással egybevágó háromszögre bontják. Az oldalak arányából és ez előbbi felbontásból is azt láthatjuk, hogy a középvonalak által alkotott háromszög területe az eredeti területének a negyed része. A középvonalakból álló háromszög magasságpontja egybeesik az eredeti háromszög köré írt kör középpontjával, ugyanis a középvonalakból álló háromszög magasságvonalai egybeesnek az eredeti háromszög oldalfelező merőlegeseivel.

Súlyvonalak és súlypont.

A háromszög csúcspontjait a szemközti oldalfelező pontokkal összekötő vonalakat súlyvonalaknak nevezzük. A három súlyvonal egy pontban metszi egymást. Ez a háromszög súlypontja: S (mely nyilvánvalóan mindig a háromszög belsejében található). A súlypont a súlyvonalaknak a csúcstól távolabb eső harmadoló pontja. Bármelyik súlyvonal a háromszöget két egyenlő területű háromszögre bontja. (Ha egy háromszöget lemezből elkészítünk, akkor a súlypontjában alátámasztva egyensúlyban lesz.)

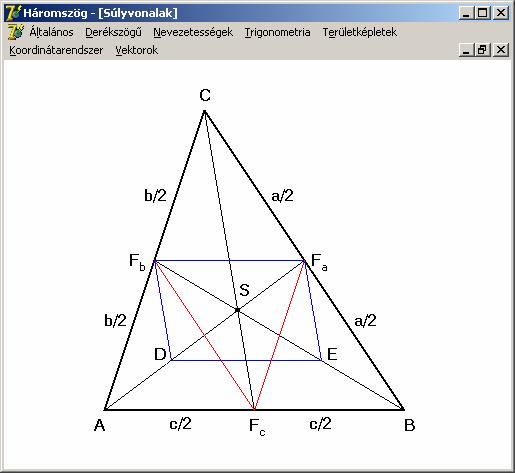
Lássunk néhány bizonyítást. A bizonyítás arra irányul, hogy az S bármely súlyvonal harmadoló pontja. A fenti rajz alapján legyen D és E az AS és a BS felezőpontja. Mivel F_aF_b az ABC háromszögnek, DE pedig az ABS háromszögnek a középvonala, ezért minkét középvonal az AB-nek a fele és párhuzamos vele. Így a DEF_aF_b négyszög egy paralelogramma, melynek átlói felezik egymást. Azaz AD = DS = SF_a, valamint BE = ES = SF_b. Ezáltal S a mindkét súlyvonal harmadoló pontja. Ugyanezeket elmondva egy másik középvonalra nyilvánvaló, hogy az S minden súlyvonalnak harmadoló pontja, azaz a három súlyvonal ugyanazon az S ponton halad át.

A második bizonyításban azt használjuk fel, hogy az ABS és F_aF_bS két hasonló háromszög, hiszen e két háromszög azonosak, egy pár csúcsszög és két pár váltószög van köztük. A hasonlóság aránya 2:1, mert F_aF_b az ABC középvonala. Ekkor viszont:

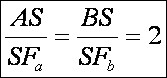
Az adódik tehát, hogy S az AF_a-nak és az BF_b-nek is a harmadoló pontja. Ugyanezt még egy középvonalra megismételve adódik, hogy az S mindhárom súlyvonal harmadoló pontja, azaz a súlyvonalak közös pontja.

A harmadik bizonyításban abból indulunk ki, hogy a középvonalakból álló F_aF_bF_c háromszög hasonló az eredeti ABC háromszöghöz. A középvonalak hossza miatt a hasonlóság aránya 1:2. Mivel párhuzamos hasonlóságról van szó, az S a hasonlóság középpontja, azaz:

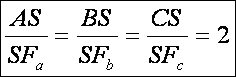
Vagyis az S mindhárom súlyvonalon harmadoló pont, ezáltal egyértelmű.

Az utolsó bizonyítás szinte csak utalás a Ceva-féle tételre, hiszen a háromszög oldalain keletkező szakaszok külön-külön egyenlők, azaz az ottani jelölés szerint: a = a’ = a/2, b = b’ = b/2 és c = c’ = c/2. Így a tétel feltétele teljesül, azaz a súlyvonalak, mint Ceva-féle szakaszok, egy ponton mennek át.

Megjegyzések: A középponti (vagy súlyponti) háromszögnek és az eredeti háromszög súlypontja egybeesik. A háromszög bármelyik középvonalának egyenese egyenlő távol halad a háromszög mindhárom csúcsától. A súlypont és a csúcsok távolságának négyzetösszege a sík bármely pontjára nézve a legkisebb. A leghosszabb súlyvonal a legrövidebb oldalhoz tartozik.

Magasságvonalak és a magasságpont.

A háromszög csúcsaiból a szemközti oldalak egyenesére bocsátott merőlegeseket a háromszög magasságvonalainak nevezzük. A három magasságvonal egy pontban metszi egymást. Ez a háromszög magasságpontja: M.

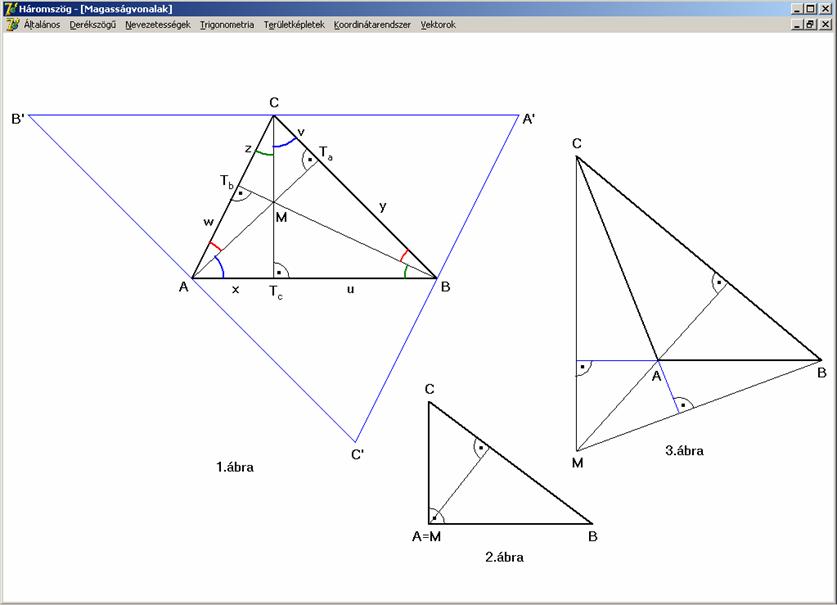
Tekintsük az előző rajz 1. ábráját. Húzzunk párhuzamosokat a csúcsokon keresztül a szemközti oldalakkal. A kapott A’B’C’ háromszögnek a középvonalai az eredeti háromszögnek az oldalai. Ha tekintjük például az AB és B’C valamint az AB’ és BC szakaszokat, akkor ezek a párhuzamosak, azaz egy paralelogrammát alkotnak. Mivel a paralelogramma szemközti oldalai egyenlők: AB = B’C és BC = AB’. Ha ezt a további oldalakra is elmondjuk, akkor nyilvánvaló, hogy az A, B és C pontok az A’B’C’ háromszög oldalfelező pontjai. Mivel CM egyenese merőleges AB-ra, merőleges a vele párhuzamos A’B’-re is. Azaz a CM egyenese az A’B’ oldal felezőmerőlegese, ahogy a többi magasság vonalai is felezőmerőlegese a megfelelő oldalnak. Az oldalfelező merőlegesekre vonatkozó tételünk értelmében ezek egy ponton mennek át, azaz a háromszög magasságvonalai is egy pontban metszik egymást.

Az 1. ábrán hegyesszögű háromszöget látunk, mely esetén a magasságpont a háromszög belsejében található. A 2. ábra derékszögű háromszöget ábrázol, a magasságpont ekkor a derékszögű csúccsal egybeesik A = M. A 3. ábrán tompaszögű háromszöget látunk, a magasságpont a tompaszög csúcsszögének a tartományában, a háromszögön kívül található.

Bizonyítsunk a Ceva tétel alapján is. Az 1. ábrán az x, u, y, v, z, és w jelöli az oldalak magasságvonalak által előállított szakaszait. Mivel az azonos színű ívvel jelölt szögek merőleges szárú szögpárok és így egyenlők, az őket tartalmazó derékszögű háromszögek hasonlók. Ezek alapján:

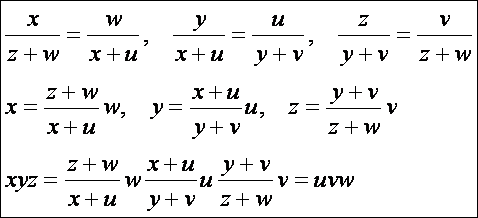
Vagyis a szakaszok teljesítik a Ceva-féle szakaszok feltételeit, azaz a három magasságvonal egy ponton halad át.

Megjegyzések: Jelölje m_a, m_b és m_c az a, b és c oldalhoz tartozó magasságokat. A háromszög két oldala úgy aránylik egymáshoz, mint a hozzájuk tartozó magasságok reciprokai.

A háromszög bármely oldalfelező pontja egyenlő távol van a másik két oldalra eső magasságtalpponttól (ugyanis az oldal Thalesz körén rajta vannak a magasságtalppontok).

Talpponti háromszög (Fagnano-feladat).

Egy hegyesszögű háromszög magasságainak talppontjai által meghatározott háromszöget talpponti háromszögnek nevezzük. Egy hegyesszögű háromszögbe írt háromszögek közül a talpponti kerülete a legkisebb.

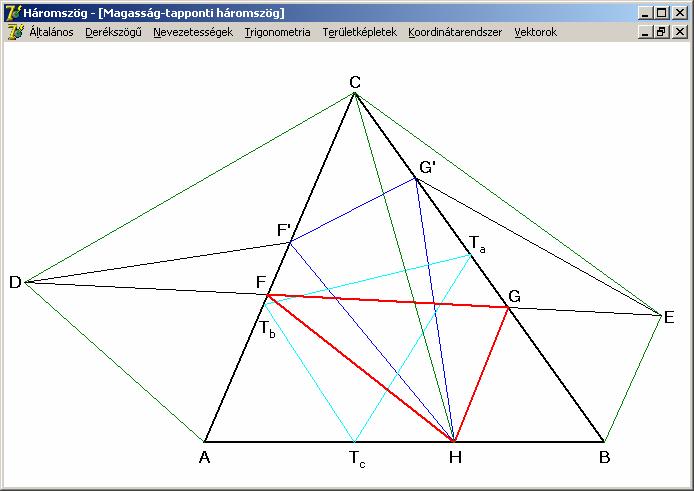
A fentebbi rajz jelöléseit használva, legyen H az AB oldal egy tetszőleges pontja. Tükrözzük H-t a másik két oldalra, AC-re tükrözve D-t, BC-re tükrözve E-t kapunk. Legyen F’ az AC, G’ pedig a BC tetszőleges belső pontja, így kapunk egy HF’G’ háromszöget. A tükrözések miatt nyilván HF’ = F’D és HG’ = G’E. Ebből az adódik, hogy a HF’G’ háromszög kerülete egyenlő a DF’G’E törött vonal hosszával. Ez viszont akkor a legrövidebb, ha a pontjai egy egyenesre, a DE szakaszra esnek, azaz F’ = F és G’ = G esetén. Tehát, ha H rögzített, akkor az FGH a legkisebb kerületű beírható háromszög. Most már csak az van hátra, hogy megkeressük, milyen H esetén lesz a háromszög a legkisebb kerületű, azaz mikor lesz a DE távolság a legkisebb. A tükrözések miatt egyrészt CD = CH = CE, tehát a CDE egyenlőszárú háromszög. Másrészt, ugyancsak a tükrözések miatt, a DCE szög mindig az ACB szög kétszerese. Itt fontos megjegyezni, hogy mivel az ABC hegyesszögű, a DCE, a DAB és ABE szögek mind kisebbek, mint 180º, Azaz az ABECD ötszög konvex, és így az F és G pontok, mint átlók metszéspontja biztosan létezik. A CDE háromszög a H lehetséges helyeire nézve mindig ugyanolyan csúcsszögű egyenlőszárú háromszög, melynek akkor a legkisebb a kerülete, és ezáltal az alapja DE, vagy ami ugyanakkor következik be, amikor a szára a lehető legkisebb. De a szár egyenlő CH-val, vagyis akkor, ha a CH a lehető legkisebb. Ez pedig akkor lesz, ha a CH az AB oldalhoz tartozó magasság. Ugyanezt a további oldalakra is elmondhatjuk, vagyis a magasságtalppontok által meghatározott háromszög kerülete a legkisebb a beírható háromszögek közül. A rajzon ez a talpponti háromszög a T_aT_bT_c háromszög.

A háromszög külső szögfelezői és a hozzáírt körök középpontjai.

A háromszög bármely két külső szög szögfelezője és a harmadik szög belső szögfelezője egy pontban metszik egymást. Ez a pont a háromszög hozzáírt körének a középpontja. Mivel a külső szögeket háromféleképpen választhatjuk meg, a háromszögeknek három hozzáírt köre van.

A tétel állítása könnyen igazolható. A hozzáírt körök középpontjai legyenek: O_A, O_B, O_C. Például az O_A pont egyenlő távol van az AB oldal meghosszabbításától (az e egyenestől) és a BC oldaltól, mivel a B csúcsnál lévő külső szög szögfelezőjén van. Hasonlóan egyenlő távol van BC oldaltól és az AC oldal meghosszabbításától (a g egyenestől), mert a C csúcsnál lévő külső szögfelezőn található. Tehát egyenlő távol van az e és g egyenesektől, azaz rajta van az A csúcsnál lévő belső szög száraitól is, vagyis rajta van ennek a belső szögnek a szögfelezőjén. Azaz az A csúcsnál lévő belső, és a B és C csúcsnál lévő külső szögfelezők átmennek az O_A ponton. Ugyanezek igazak a további hozzáírt kör középpontjára is.

A hozzáírt körök az oldalak egyeneseit a szembeni csúcstól s távolságra érinti. Az igazoláshoz használjuk fel, hogy a körhöz, adott külső pontból húzott érintőszakaszok hossza egyenlő

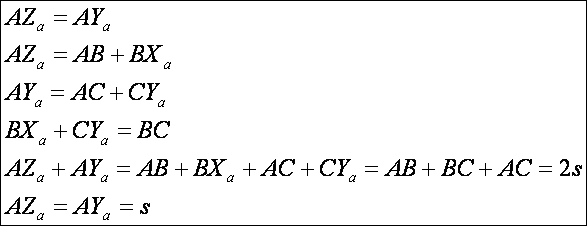
A hozzáírt körök sugarait így számolhatjuk ki: r_A = T/(s-a), r_B = T/(s-b), r_C = T/(s-c), ahol T a háromszög területe, s pedig a fél-kerület. Az r_A = T/(s-a) bizonyításhoz felírjuk az ABC háromszög területét az ABO_A, az ACO_A és a BCO_A háromszögek területével (az első kettő területéből kivonjuk a harmadik területét).

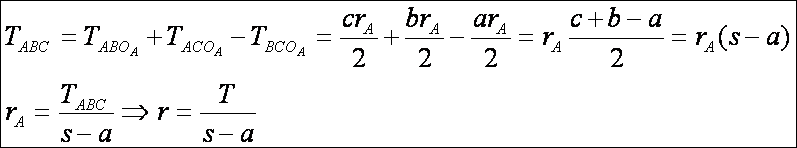
A további két sugarat ezzel analóg módon kaphatjuk meg.

Következő lap: http://gorbem.hu/MT/Haromszog5.htm