Háromszögek (2)

Vissza: http://gorbem.hu/Matematika.php

A párhuzamos szelők tétele

A továbbiakban többször felhasználjuk a párhuzamos szelők tételét, mely a következőt állítja: ha egy szög szárait párhuzamosokkal metsszük, akkor az egyik száron keletkező szakaszok hosszának az aránya megegyezik a másik száron keletkező megfelelő szakaszok hosszának az arányával. Szokás ezt a tételt a párhuzamos szelők első tételének is nevezni.

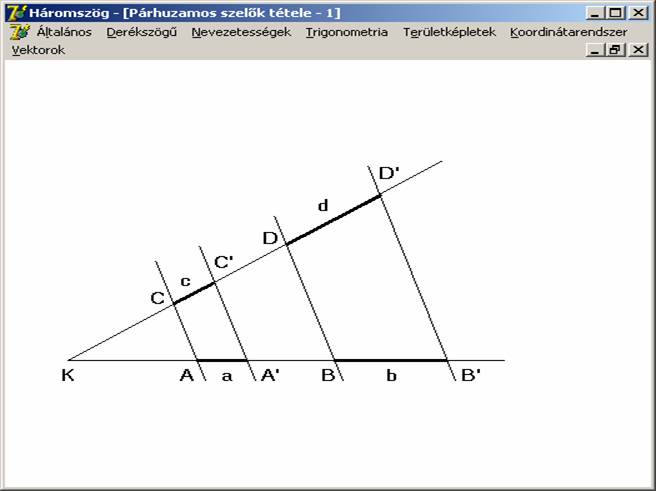
Az ábra szerint tehát:

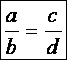
A tétel bizonyítása. A bizonyítás során óvatosan kell eljárni. Egyrészt azért, mert nem használhatjuk fel az egymással középpontosan hasonló háromszögek azon tulajdonságát, hogy a megfelelő oldalak aránya azonos, mert ez éppen a párhuzamos szelők tételének a következménye. A második gond az, hogy itt szakaszok arányáról kell nyilatkozni. Összemérhető szakaszok esetén ez nem probléma (van olyan egységnek válaszható szakasz, amelynek minden használt szakasz a többese). De ha a szakaszok nem összemérhetők, azaz hosszúságuk aránya irracionális szám, akkor az analízis eszközeit (határértéket) is használni kell a tétel igazolásakor. A bizonyítást három lépésben hajtjuk végre.

Először (a következő rajz 1. ábrája) azt látjuk be, hogy ha az egyik szögszáron egyenlő hosszú szakaszokat veszünk fel, akkor a másik szögszáron is azonos hosszúságú szakaszok keletkeznek. Legyen tehát AB = CD. A CDFE négyszög az ABB’A’-nek az AC hosszúsággal történt párhuzamos eltolása, tehát egybevágók (szögeik az egyállású szögek egyenlősége miatt azonos). Ugyanezen okok miatt a GHD’C’ négyszög a CDFE négyszögnek a DH hosszúsággal történt párhuzamos eltolása, tehát ezek is egybevágók. Mivel az egybevágóság tranzitív, így az ABB’A’ és GHD’C’ is egybevágók, azaz A’B’ = C’D’, amit bizonyítanunk kellett.

Másodszor, ha az AB és CD szakaszok összemérhetők és a két szakasz aránya a : b = n : k, (ahol n és k pozitív egész, és ebben az esetben a 2. ábrán a piros szakasz éppen a B’D’-re esik), akkor:

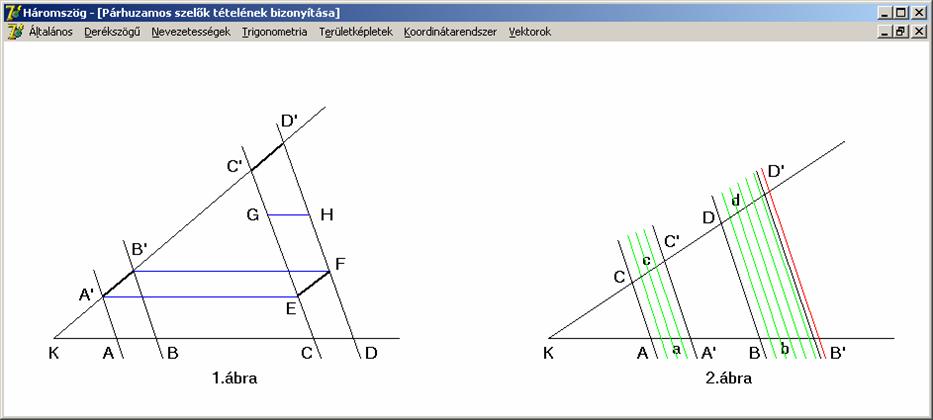
Harmadik lépésben tetszőleges arányra bizonyítunk (a rajz 2. ábrája). Osszuk fel az AA’ szakaszt n egyenlő részre (a rajzon ez 4), és a keletkező osztópontokon keresztül húzzunk párhuzamosokat a meglévő szelőkkel. A B ponttól kezdve egymás után mérjük fel az AA’/n hosszúságú szakaszokat addig, amíg éppen túljutunk a B’ ponton (ez a k+1. lépésben következzék be, a rajzon ez 6), és itt is a keletkező pontokon keresztül rajzoljuk meg a szelőket (a piros színű már éppen túlkerült a B’ ponton). Az első rész állítása miatt a másik száron keletkező (zöld szelők által kijelölt) szakaszok is egyenlő hosszúak. Ezek alapján a következők igazak, amelyek a tétel állítását igazolják:

A továbbiakban természetesen a bizonyításokban felhasználhatjuk a párhuzamos szakaszok első tételét, valamint a középpontosan hasonló háromszögek oldalaira vonatkozó arányok azonosságát. A párhuzamos szelők tételében alapértelmezésben négy szelő egyenes feltételezünk. Az állítás természetesen akkor is igaz, ha ezekből kettő-három egybeesik és valójában három, vagy csak két párhuzamos metszi a szögszárakat. (Ezt úgy is felfoghatjuk, hogy a hiányzó párhuzamosok a szög szárait a szög csúcsában, K-ban metszik. Ezeket halványabban az ábrán is feltüntettük.)

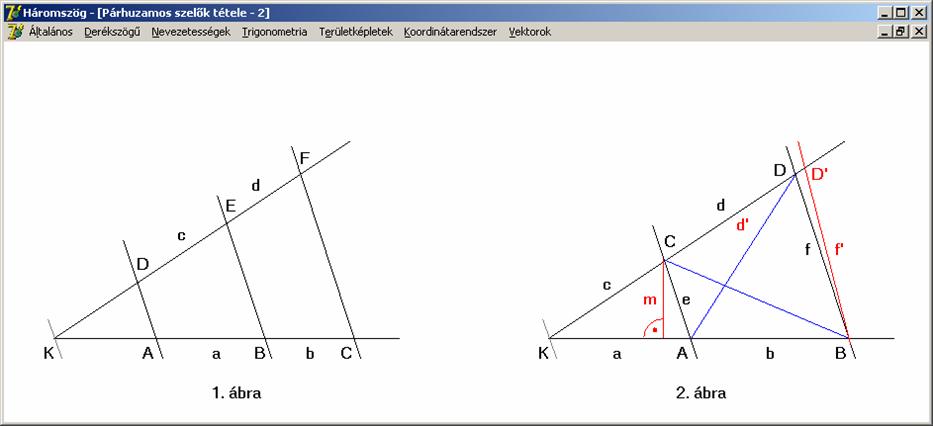
Mivel jelöléseink nem változtak, a helyes arányt itt is a fenti képlet szolgáltatja. Lássuk a tételnek a bizonyítását a keletkezett háromszögek területének arányait felhasználva, a 2. ábra alapján.

A párhuzamos szelők első tételének megfordítása: ha egy szög szárain elhelyezkedő megfelelő szakaszok aránya megegyezik, akkor a szakaszokat meghatározó, a szög szárait metsző egyenesek egymással párhuzamosak.

Bizonyítás (az előző rajz 2. ábrája alapján), indirekt módon: tegyük fel az állítással szemben, hogy

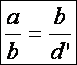
(ahol d’ = CD’), de e és f’=BD’ nem párhuzamos (azaz D<>D’). Természetesen van olyan a B-re illeszkedő f egyenes, amely párhuzamos e-vel, ezáltal a párhuzamos szelők tétele értelmében:

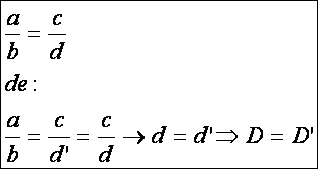
Vagyis indirekt feltevésünkkel ellentétben e és f párhuzamosak.

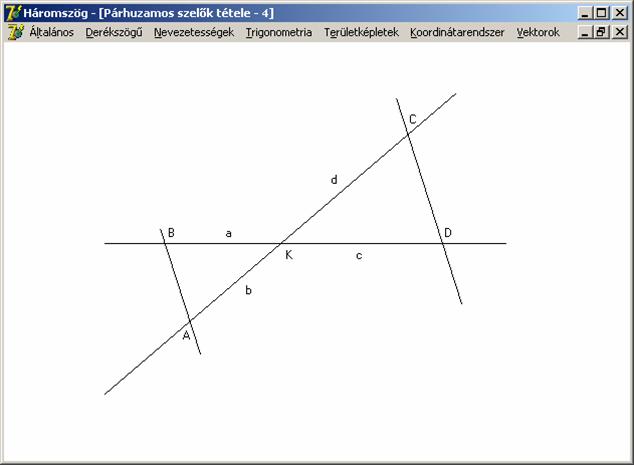
Tétel: Egy szög szárait metsző párhuzamosokból a szárak által kimetszett szakaszok aránya egyenlő, a párhuzamosok által az egyes szárakból lemetszett szakaszok arányával. Szokás ezt a párhuzamos szelők második tételének (vagy párhuzamos szelőszakaszok tételének) nevezni.

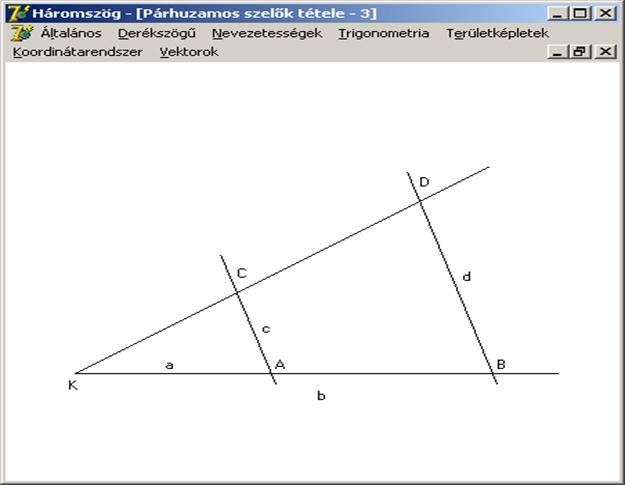
Tehát a második tételben nem a szög szárain, hanem az egyik szögszáron és a szárak közötti szakaszok arányáról beszélünk.

A helyes ábraértelmezés miatt:

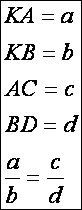
Mivel a KAC háromszög és a KBD háromszög egymáshoz hasonló (szögeik egyenlők, mivel egyállásúak), így az egymásnak megfelelő oldalak aránya egyenlő:

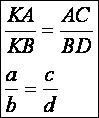
A párhuzamos szelők második tételének megfordítása: ha egy szög szárain elhelyezkedő megfelelő szakaszok aránya megegyezik a metsző egyeneseknek a szög szárai közé eső szakaszok arányával, akkor a szakaszokat meghatározó, a szög szárait metsző egyenesek egymással párhuzamosak. Bizonyítása az első tétel megfordításával teljesen analóg módon történik.

A párhuzamos szelőkre vonatkozó mindkét tétel és azok megfordításai igazak abban az estben is, ha a szög szárai helyett a szögszárak egyeneseit szerepeltetjük a tételekben. Például két párhuzamos esetén az első tétel:

Megjegyzés: A párhuzamos szelők tételének segítségével az a, b és c szakaszokhoz tudunk olyan x ismeretlen szakaszt szerkeszteni, amelyre. a/b = c/x. Ez a negyedik arányos szerkesztése. Ugyancsak a párhuzamos szelők tétele alapján lehet egy szakaszt megadott két szakasz arányában felosztani.

Szelőszakaszok tétele (szelőtétel). Egy körhöz, egy adott külső pontból húzott szelőszakaszok hosszának szorzata állandó.

A következő rajz jelölései szerint az ABC szög és az ADC szög a kerületi szögek tétele értelmében (lásd: Haromszog3.htm lap) egyenlők. A PBC és PAD háromszögekben a P csúcsnál lévő szög közös, így ezek hasonló háromszögek. Tehát:

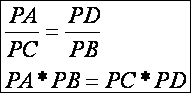
Ez viszont a tétel állítását jelenti.

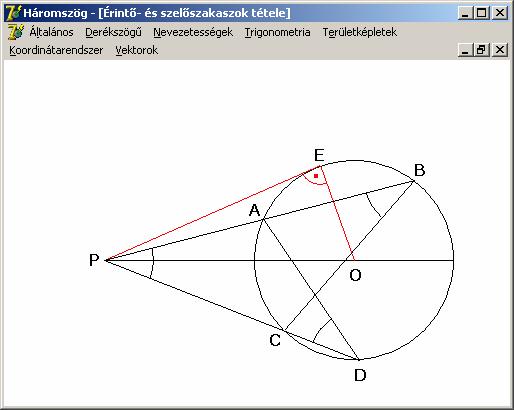
Érintő- és szelőszakaszok tétele. Egy körhöz, egy adott külső pontból húzott érintő szakasz hossza az adott pontból húzott szelőszakaszok hosszának a mértani közepe.

A tétel a szelőszakaszok tételének speciális esete. Legyen ugyanis A = B = E (az előző rajz alapján), ahol PE a kör érintője. Ekkor az előző tétel értelmében:

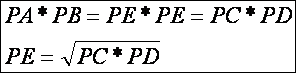
Szögfelezőtétel. A háromszög bármely belső szögfelezője a szöggel szemközti oldalt a szomszédos oldalak arányában osztja.

A bizonyításnál a rajz 1. ábrájának jelöléseit használva: rajzoljuk meg a C csúcsnál lévő szög f belső szögfelezőjét, amely az F ponttal a c oldalt x és y hosszúságú szakaszokra bontja. Majd mérjük fel az a oldalt a b oldalnak a C csúcson túli meghosszabbítására, így kapjuk a D pontot. A BCD háromszög nyilván egyenlő szárú, tehát a BD oldal m felezőmerőlegese az ABC háromszög C csúcsánál lévő külső szög szögfelezője. Mivel az egy csúcsnál lévő belső és külső szögfelezők merőlegesek egymásra, az f szakasz párhuzamos a BD oldallal. Most már alkalmazhatjuk a párhuzamos szelők első tételét, amivel a szögfelezőtétel állításához jutunk:

.

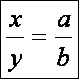A tétel állítását beláthatjuk területek segítségével is (h az F és AC valamint F és BC távolsága, így magasságok az CFA és CFB háromszögekben):

Külsőszögfelező-tétel: Ha egy háromszög külső szögfelezője metszi a szöggel szemközti oldalt, akkor a metszéspontnak az oldal végpontjaiból mért távolságai úgy aránylanak egymáshoz, mint a szemközti csúcsból az ezekhez a végpontokhoz vezető oldalak hossza.

Bizonyításhoz használjuk az előző rajz 2. ábráját: az f_k külső szögfelező csak akkor metszi az AB oldal egyenesét, ha az a és b oldal nem egyenlő, azaz a háromszög nem egyenlő szárú. Ezért legyen b > a, amint az a rajzon is látható. Ha a D-t úgy választjuk meg, hogy CD = CB = a, akkor a DB-re merőleges f_b a C-nél lévő belső szöget felezi, így f_b és f_k egymásra merőleges, amiből CE és BD párhuzamossága következik. Tehát alkalmazhatjuk a párhuzamos szelők tételét, ami a tétel igazolását jelenti:

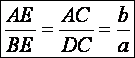
Ceva és Menelaosz tétele

Osztóviszony: ha A, B és C egy egyenes három pontja, akkor az hányadost a pontok osztóviszonyának (vagy egyszerű viszonyának) nevezzük, ahol a szakaszokat irányítottan vesszük figyelembe (azaz: PA = -AP). Az osztóviszony az affin geometria egyik invariánsa.

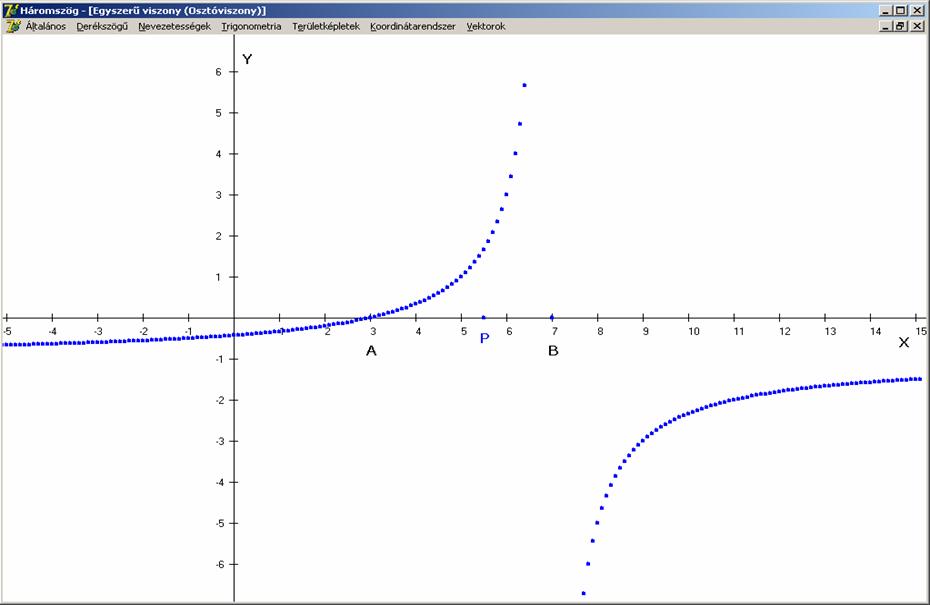
A következő grafikon az AP/PB hányados értékét ábrázoltuk a P függvényében, rögzített A = 3 és B = 7 mellett (a pontok az x tengelyen vannak, az y tengelyen pedig az osztóviszony értéke). Nyilvánvaló, hogy a P pont nem eshet a B pontra (a tört nevezője nem lehet nulla), ha pedig A-val megegyezik, akkor az osztóviszony értéke nulla.

Azt az egyenes szakaszt, mely egy háromszög csúcsát a szemközti oldala egyenesének egy adott pontjával köti össze, Ceva-féle szakasznak nevezzük. A következő (1. – 3.) tételekben ilyen Ceva-féle szakaszok szerepelnek.

1. Tétel: Ha egy ABC háromszög esetén megrajzolunk három darab, egy adott P ponton átmenő Ceva-féle szakaszt, akkor az oldalakon keletkező szakaszok osztóviszonyai között fennáll a következő összefüggés:

(BCX)(CAY)(ABZ) = 1

A következő rajz 1. 2. és 3. ábráján láthatjuk a P helye szerinti különböző eseteket. A 4. ábrán egy ezektől lényegesen különböző eset látható, ekkor a Z a végtelen távolban lévő pont, mert a CP az AB-vel párhuzamos.

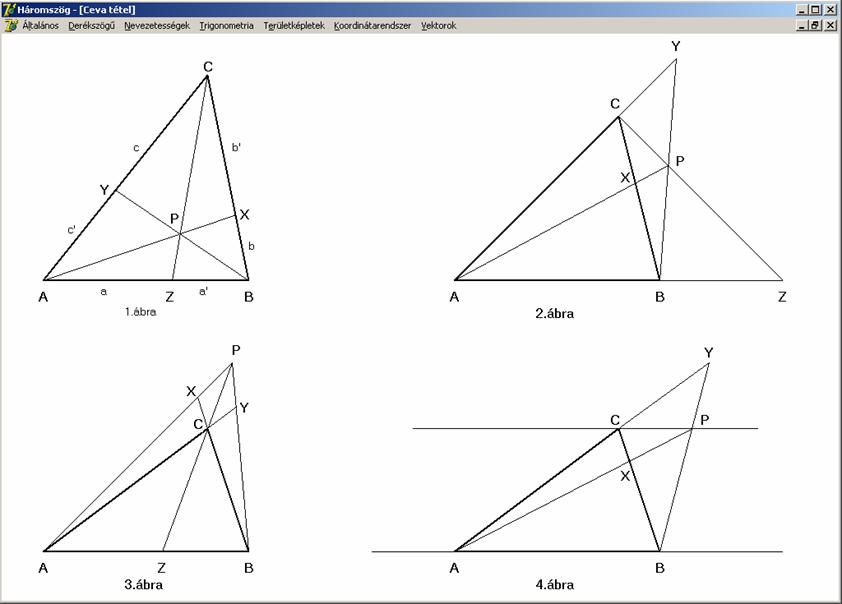
Lássuk az 1. ábrán látható eset bizonyítását. Először írjuk át az osztóviszonyt tört alakba, majd felírjuk a háromszög oldalain keletkező szakaszok arányát a rajtuk elhelyezkedő háromszögek területének segítségével (közös a magasságuk, ezért a területük aránya megegyezik az oldalakra eső szakaszok – alapok – arányával):

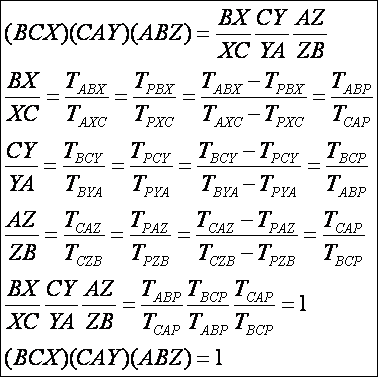
Megjegyzés: az előző egyenletekben a következő algebrai átalakítást használtuk fel:

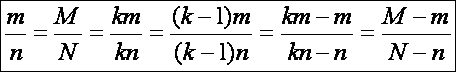
2. Tétel: Ha az ABC háromszögben úgy veszünk fel egy adott P ponton átmenő Ceva-féle szakaszokat, hogy a C csúcsból kiinduló a végtelen távoli pontban metszené az AB egyenesét (azaz párhuzamos vele – az előző rajz 4. ábrája), akkor az oldalakon keletkező szakaszok osztóviszonyai között fennáll a következő összefüggés:

(BCX)(CAY) = -1

Bizonyításnál felhasználjuk, hogy az ABX és XPC háromszögek hasonlóak (szögeik egyenlők), illetve a párhuzamos szelőszakaszok tételét:

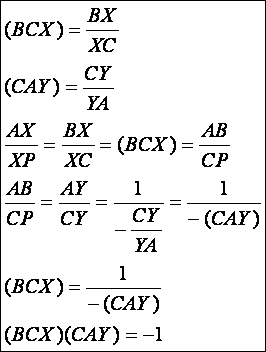
3. Tétel: Ha az ABC háromszög oldal-egyenesein az X, Y és Z pontok úgy helyezkednek el, hogy AX, BY és CZ szakaszok párhuzamosak (a végtelen távoli pontban metszenék egymást), akkor az oldal-egyeneseken keletkező szakaszok osztóviszonyai között fennáll a következő összefüggés:

(ABZ)(BCX)(CAY) = 1

Ezt a következő rajzon szemléltettük:

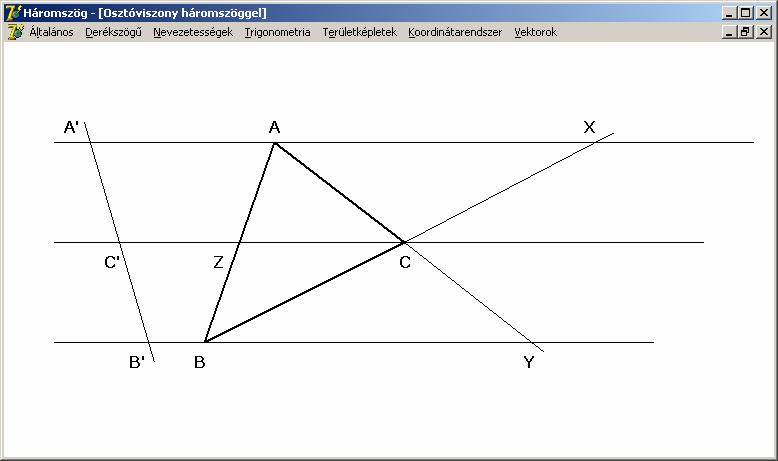
Bizonyítás: a párhuzamos szelők tétele miatt az arányokat kifejező egyszerű viszonyok egyenlők: (ABZ) = (AYC) = (XBC) = (A’B’C’). Ugyanakkor:

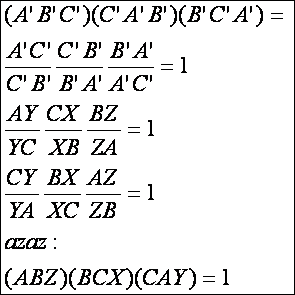
Az 1., 2. és 3. tétel állításait foglalja össze a következő:

Ceva tétele. Ha egy ABC háromszög AB, BC, CA oldal-egyenesein a csúcsoktól különböző Z, X és Y pontok (rendre) úgy helyezkednek el, hogy az osztóviszonyokra (ABZ)(BCX)(CAY) = 1, akkor az AX, BY és CZ egyenesek vagy egy ponton mennek át, vagy párhuzamosak (a végtelen távoli pontra illeszkednek). A tétel megfordítása is igaz. A háromszög oldalain keletkező (fentebbi rajz 1. ábra szerinti) szakaszokra érvényes a következő: abc = a’b’c’.

4. Tétel: Ha egy egyenes az ABC háromszög oldal-egyeneseit a csúcsoktól különböző X, Y és Z pontokban metszi, akkor az oldal-egyeneseken keletkező szakaszok osztóviszonyai között fennáll a következő összefüggés:

(BCX)(CAY)(ABZ) = -1

A lehetséges eseteket a következő rajz 1., 2. és 3. ábráján szemléltettük.

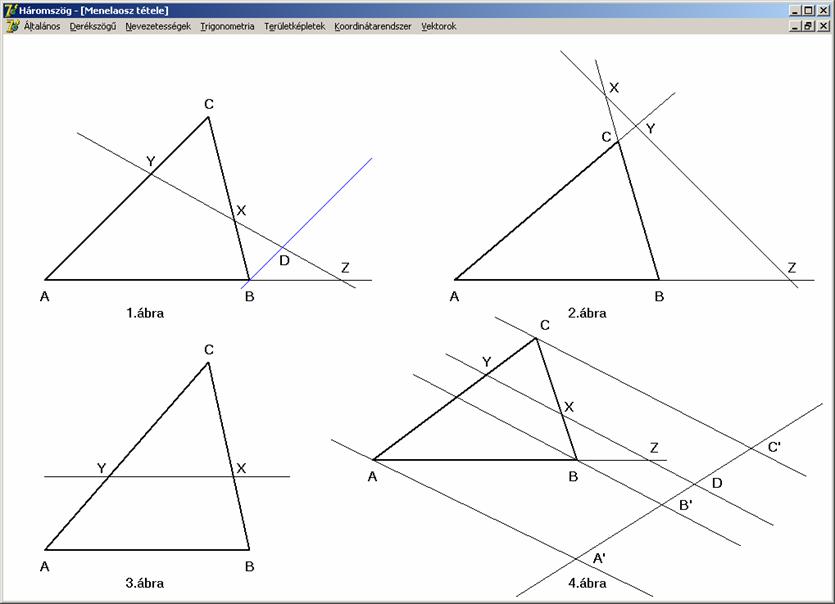
A tétel bizonyítását lássuk az 1. ábra alapján. Húzzunk párhuzamost az AC oldallal a B csúcson keresztül. Ez az X, Y, Z pontok egyenesét a D pontban metszi. Ekkor az AZY és BZD hasonló háromszögek. Ugyancsak hasonlóak a CYX és BDX háromszögek is. Ezeknek a hasonló háromszögeknek az oldalai arányát felhasználva kapjuk:

Ugyanehhez az eredményhez jutunk a 4. ábra alapján, ha átírjuk az osztóviszonyokat az A’, B’, D és C’ pontok alkotott szakaszokra. Ugyanis a párhuzamos szelők tétele miatt:

Így elég azt belátni, hogy:

Ha beírjuk az osztóviszonyok jelentését, akkor láthatjuk, hogy helyes az állítás (minden szakasz, mindkét előjellel szerepel):

5. Tétel: Ha egy ABC háromszög AB oldalával párhuzamos egyenes a másik két oldalt a csúcsoktól különböző pontokban metszi, akkor az oldal-egyeneseken keletkező szakaszok osztóviszonyai között fennáll a következő összefüggés:

(BCX)(CAY) = -1

Ezt a tételt az előző rajz 3. ábráján szemléltettük. A párhuzamos szelők tétele miatt:

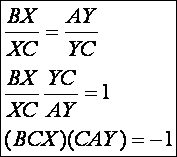
A 4. tétel megfordítása a következő:

Menelaos tétele. Ha egy ABC háromszög AB, BC, CA oldal-egyenesein a csúcsoktól különböző Z, X és Y pontok (rendre) úgy helyezkednek el, hogy az osztóviszonyokra (ABZ)(BCX)(CAY) = -1, akkor az X, Y és Z pontok egy egyenesen vannak.

Bizonyítás: Az X és Y pontok különbözőek, mert ha nem lennének, akkor a C csúcsra esnének. Az XY egyenes nem lehet az AB-vel párhuzamos, mert akkor a jelen és az előző tétel alapján (ABZ) = -1 adódna, pedig az egyszerű viszony értéke nem lehet -1. Messe a fentebbi rajz alapján az AB egyenest az XY egyenes a Z’ pontban. Azt kell tehát belátnunk, hogy Z’ = Z. A 4. tétel szerint: (BCX)(CAY)(ABZ) = -1, amit ha a jelen tétel állításával összevetjük, akkor azt kapjuk, hogy (ABZ) = (ABZ’). Ebből viszont az adódik, hogy Z = Z’.

Megjegyzés: néha az általunk Menelaos tételnek és megfordításának nevezett tételeket egy tételben mondják ki, és ezt nevezik együtt Menelaos tételnek.

A Ceva tétel bizonyítása a Menelaosz tétel segítségével. Tekintsük a következő rajzot:

Alkalmazzuk a Menelaosz tételt az ABY és a BCY háromszögekre, majd a felírt egyenleteket szorozzuk össze:

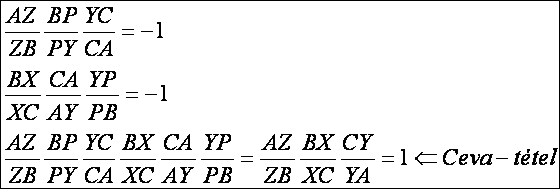
A Ceva tétel a szinusz tétel segítségével trigonometrikus alakban is felírható:

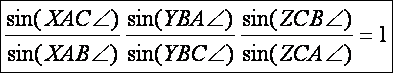
Kettősviszony: ha A, B,C és D egy egyenes négy pontja, akkor az hányadost, vagyis az (ABC) és (ABD) osztóviszonyok hányadosát a pontok kettősviszonyának nevezzük, ahol a szakaszokat irányítottan vesszük figyelembe. A kettősviszony a projektív geometria legfontosabb invariánsa.

Következő lap: http://gorbem.hu/MT/Haromszog3.htm