Háromszögek (1)

Vissza: http://gorbem.hu/Matematika.php

Ebben a cikksorozatban a háromszögekről lesz szó. De nem foglalkozunk a tárgyalásához feltétlen szükséges geometriai alapfogalmak bevezetésével. Például a térelemekkel (pont, egyenes, sík és tér), azok illeszkedésével, a párhuzamossággal, a térelemek mérésével (távolság, szög nagysága, terület, térfogat), a szög, a kör, a gömb alapvető tulajdonságaival, az egybevágóság, a szimmetria és hasonlóság általános fogalmaival, a koordinátarendszerekkel és vektorokkal. Az ezekkel kapcsolatos legalapvetőbb tulajdonságokat a továbbiakban mind ismertnek tételezzük fel. Mivel a háromszög a legkisebb oldalszámú sokszög, ezért bevezetésként essen néhány szó a sokszögekről.

Néhány szó a sokszögekről

A sokszög fogalma. A geometriában az egymáshoz kapcsolódó egyenes szakaszok sorozatát töröttvonalnak nevezzük (megkülönböztetve a törtvonaltól, melyet az osztás jelölésére használunk). Ha az első szakasz kezdőpontja és az utolsó szakasz végpontja megegyezik, akkor a töröttvonal zárt. Ha egy síkbeli zárt töröttvonalban a szakaszoknak csak végpontjaikban van közös pontjuk, és minden végpont pontosan két szakaszhoz tartozik (azaz a töröttvonal önmagát nem metszi), akkor az ilyen egyszerű töröttvonalat sokszögnek, vagy poligonnak nevezzük (ezen a lapon csak ilyen, egyszerű sokszögekkel foglalkozunk). Ebben az esetben a szakaszokat oldalaknak, a szakaszok végpontjait csúcsoknak hívjuk. Egy sokszög, a síkját két részre osztja. A körbezárt véges rész, a sokszög belseje. Ha egy sokszög oldalainak és csúcsainak száma n, akkor n-szögről beszélünk. Nyilvánvaló, hogy az Euklideszi geometriában az n ≥ 3. (Például a gömbi geometriában létezik két-szög is: két teljes főkör – mint az ottani egyenesek – két darab két-szöget is létrehoz.) Két egymáshoz csúcsban kapcsolódó oldal által bezárt belső (tehát a sokszög belsejébe eső) szöget (töröttvonal esetén szokás ezt törésszögnek nevezni) a sokszög csúcsszögének (vagy egyszerűen csak szögének) nevezzük. Így az n-szögnek – a nevének megfelelően – n darab szöge van. A definíció alapján nem kizárt, hogy egy csúcsszög értéke 180º legyen. Ebben az esetben – a hétköznapi értelemben – a két szomszédos oldal nem is zár be szöget, hiszen ugyanolyan állású. Szokás az ilyen sokszögeket elfajuló sokszögeknek is nevezni. Ha például egy négyszögnek, van 180º-os szöge (három csúcsa egy egyenesen van – mind a négy nem lehet egy egyenesen, mert az ellentmond a sokszög definíciójának), akkor azt (az egyállású két oldalát egynek tekintve) háromszögnek, vagy elfajuló négyszögnek tekinthetjük. Ha n-szögekről beszélünk, általában nem értjük bele az elfajuló sokszögeket, vagyis nem lehet 180º-os fokos szöge.

Konvex és konkáv sokszögek. Ha egy sokszög minden szöge kisebb, mint 180º, akkor a sokszöget konvexnek nevezzük. Ha létezik 180º-nál nagyobb szöge, akkor a sokszög konkáv. (Általában konvexnek nevezünk egy síkidomot, ha a síkidom bármely két pontját összekötő szakasznak minden pontjai a síkidomhoz tartozik. A konvex sokszög bármely belső pontjából a sokszög kerületének bármely pontja „takarás nélkül” látható.) Egy sokszögnek minden csúcsánál van külső szöge. Konvex sokszög esetén a külső szög az a szög, amely az ottani belső szög mellékszöge (180º-ra kiegészítő). Ha konkáv csúcs esetén ezt az értéket negatívnak vesszük (ekkor a külső szög a sokszög belsejébe esik, így nem igazán külső szög), akkor egy sokszög külső szögeinek összege mindig 360º lesz. Nyilvánvaló, hogy egy konkáv sokszög oldalainak száma legalább négy (mivel a konkáv szöge már eleve nagyobb, mint egy háromszög szögeinek összege). A továbbiakban sokszög alatt mindig konvex sokszöget értünk. (ha nem, akkor azt külön jelezni fogjuk).

Sokszögek megadása. Egy n oldalú sokszöget 2n - 3 adattal adhatunk meg egyértelműen. Próbáljuk meg ennek a helyességét belátni. Kezdjük azzal, hogy két sokszög egybevágó, ha az egymásnak megfelelő oldalai és szögei (vagy oldalai és átlói) egymással egyenlők. Ebből azt gondolhatnánk, hogy egy sokszög megadásához meg kell adni minden oldalát és minden szögét (vagy átlóját). Ez azonban túlhatározott megadás lenne, mert nem biztos, hogy bármely ilyen adathalmazhoz tartozna sokszög (például lehet, hogy nem záródna a töröttvonal). Ezek az adatok ugyanis nem függetlenek egymástól. Például a szögek összegének (n - 2)*180º-nak kell lenni, amint azt a későbbiekben be is bizonyítjuk. Ha viszont a meghatározó adatokat például úgy választjuk meg, hogy egy oldal és a következő oldallal bezárt szög, majd ezt ismételve addig folytatjuk, amíg az utolsó oldalhoz nem érünk, akkor az utolsó oldalt és az utolsó két szöget már nem kell megadni, hiszen azok az előzőekből már egyértelműen adódnak. Azaz a 2n adatból (n oldal + n szög), nem kell megadni egy oldalt és két szöget, vagyis 2n-nél hárommal kevesebb adat elegendő az egyértelmű megadáshoz, azaz csak 2n - 3 adat szükséges és elégséges. Hatszög esetén ez így néz ki (a pirossal rajzolt oldal és a szögek már a többiek által adottak):

Ugyanezt kapjuk akkor is, ha oldalak és átlók segítségével adjuk meg a sokszöget. Egy oldal megrajzolása után két csúcs, minden további oldal és átló (utolsónál két oldal, de mindig két adat) után további egy-egy csúcs lesz meghatározva. Tehát a csúcs (n) – adat párok sora: 2 – 1, 3 – 3, 4 – 5, 5 – 7, 6 – 9 … Azaz a képlet valóban: 2n - 3. Mindezt egy rajzon szemléltettük:

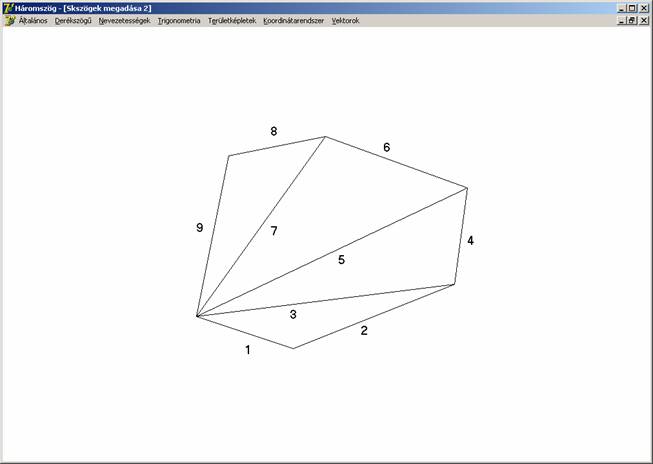
Ez az érték adódik akkor is, ha a sokszöget egy koordinátarendszerben adjuk meg. Ekkor minden csúcspontjának két koordinátája van, így látszólag 2n adatra lenne szükség. De a sokszöget meghatározó adatok (oldalhosszak, átlók hossza és szögei nagysága) függetlenek a sokszög koordinátarendszerben elfoglalt helyétől. Vagyis felvehető a sokszög úgy, hogy az egyik csúcsa az origóban, egy másik pedig valamelyik koordinátatengelyen helyezkedjen el. Ekkor viszont a koordináták között három nulla lesz (bármely sokszög esetén tehát ezek ismertek, eleve adottak lesznek), így a 2n-nél hárommal kevesebb adat kell a sokszög megadásához, azaz valóban 2n-3 adat szükséges és elégséges is. Egy konkrét esetet itt is lerajzoltunk:

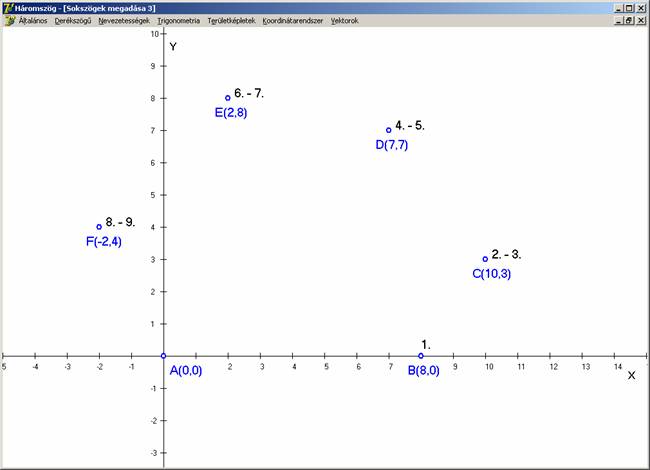
Az egybevágóság megfogalmazására visszatérve, van itt még egy dolog. Ez pedig az egymásnak megfelelő utalás. Az adataink nem tekinthetők egyszerű halmaznak, azaz az adatokat nem szabad összekeverni, rendezettnek kell tekinteni, mert ha tetszőleges sorrendben használjuk fel őket, akkor hiába lesznek a két sokszögnek ugyanolyan hosszúak a megadott oldalai és ugyanakkorák a megadott szögei, a két sokszög nem lesz egybevágó. Nézzünk ezekre példákat.

Az alól, hogy az adatok sorrendje lényeges, még a háromszögek sem kivételek. Ha a három oldalával adjuk meg a háromszöget, akkor két egybevágó, ellentétes körüljárású háromszögből kapjuk az egyiket. De ha két oldallal és az egyik oldallal szemközti szöggel, akkor nem mindegy, hogy a nagyobbik, vagy a kisebbik oldallal szemközti a szög, mert utóbbi esetben két nem egybevágó háromszög is szerkeszthető az adatokból. Ezt láthatjuk az alábbi rajz 1. ábráján. Megjegyezzük még azt, hogy ha az a oldal nagyságát változtatjuk, akkor a következő esetek lehetségesek:

1. esetén nem szerkeszthető háromszög;

2. esetén egy derékszögű háromszög szerkeszthető;

3. esetén ABC és ABC’, azaz két háromszög szerkeszthető, ahol nyilvánvaló, hogy b > b’;

4. a > c esetén egy háromszög szerkeszthető (vagyis csak akkor lesz egyértelmű a háromszög, ha a nagyobb oldallal szemközti szög adott).

Négyszögek esetén viszont nagyon könnyen kaphatunk nem egybevágó négyszögeket az adatok megcserélésével. Ez látható az alábbi rajz 2. ábráján. Az ott látható két négyszög nem egybevágó, pedig ugyanabból az adathalmazból lett megszerkesztve, csak a 4 és 5 hosszúságú oldalakat a második négyszögben az elsőhöz képest megcserélve használtuk fel.

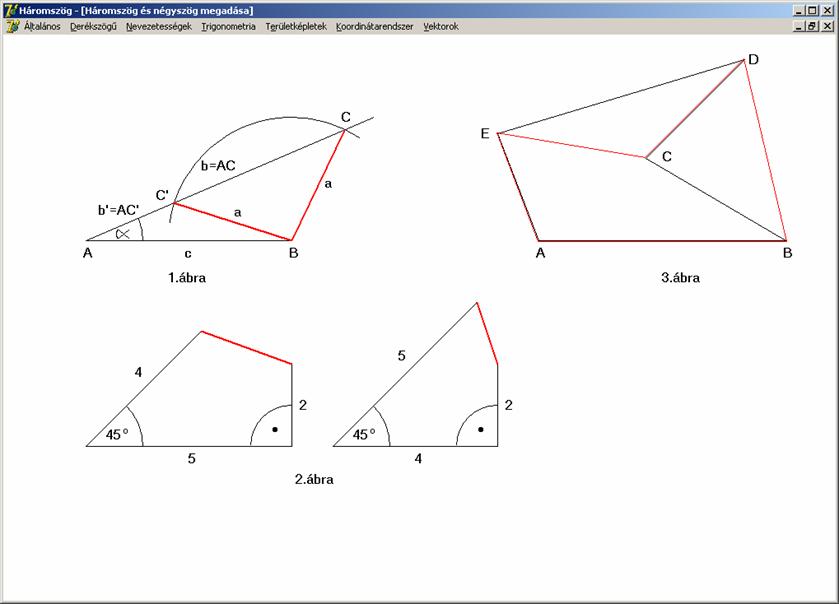
Hasonló a helyzet koordinátarendszerben történő megadásnál is. Konvex esetén egyértelmű az oldalak megrajzolása. Konkáv esetnél viszont tartani kell a megadott sorrendet. Ugyanis, ha megrajzoljuk (megadjuk) a sokszög csúcsait (a koordináták alapján), akkor azok összekötése (az oldalak) még nem lesznek egyértelműek, ugyanahhoz a ponthalmazhoz többféle sokszög tartozhat. Nem mindegy, hogy melyik lesz oldal és melyik átló, amint az a fentebbi rajz 3. ábráján is megfigyelhető, a fekete (ABCDE) és piros (ABDCE) konkáv ötszög bizony nem egybevágó.

Érdemes itt néhány szót szólni a szabályos sokszögekről. Egy sokszög szabályos, ha minden oldala és minden szöge egyenlő. Ezeket a sokszögeket egyetlen hosszúsági adattal megadhatjuk, például oldalával, beírt, vagy körülírt körének sugarával. A megszerkesztés viszont már egy érdekes dolog. Hiába a meghatározottság, a szerkesztést (Euklideszi) csak bizonyos oldalszám esetén tudjuk végrehajtani. Szabályos sokszög pontosan akkor szerkeszthető egy adott körben, ha az oldalak számára (n) érvényes a következő: n = 2^s p₁p₂…p_r, ahol s természetes szám, p_i olyan páratlan prímszámok, hogy p_i-1 a 2-nek hatványa. Vagyis: n = 3, 4, 5, 6, 8, 10, 12, …

Két nem szomszédos csúcsot összekötő (konvex sokszögeknél a sokszög belsejében haladó) szakasz neve átló. Egy n-szögben az átlók száma n*(n - 3)/2. Indoklás: mivel minden csúcsból n - 3 húzható – mert önmagába nem húzható átló, a szomszédos csúcsokba pedig oldal húzható – , ez szorozva n-el, mivel n csúcs van, de minden átló két csúcshoz tartozik, vagyis így kétszer lenne figyelembe véve, ezért osztva 2-vel. Egy sokszöget az egy csúcsából kiinduló átlók háromszögekre vágják szét. Ezek száma: (n – 3) + 1 = n - 2 (minden vágással egy újabb háromszög keletkezik, de a végén egy négyszög marad, így az utolsó vágás már két háromszöget hoz létre, ezért a +1). Ezek alapján a sokszög belső szögeinek összege: (n - 2)*180º, mivel a sokszög belső szögei a háromszögek szögeivé darabolódnak szét. (Itt felhasználtuk azt a tényt, hogy a háromszög belső szögeinek összege az Euklideszi geometriában 180º.) A sokszög területe, ezen háromszögek területeinek összege. Kerülete természetesen az oldalak hosszának az összege. Mindezek alapján kijelenthetjük, hogy a sokszögek tulajdonságainak megismerése csak a háromszögek minél alaposabb ismerete alapján lehetséges. A továbbiakban tehát a háromszögekkel foglalkozunk.

A háromszögekről általában

Háromszögek. Tehát a 3-oldalú sokszögeket háromszögeknek nevezzük. Csúcsait az angol abc nagy betűivel, oldalait kisbetűkkel, szögeit pedig a görög abc betűivel szokás jelölni. Ha csak egy háromszögünk van, akkor ezek az azonosítók lehetnek rendre: A, B és C, a, b és c valamint α, β és γ. Alapértelmezésben az a oldallal szemben az A csúcs és az α szög, a b oldallal szemben a B csúcs és a β szög, míg a c oldallal szemben a C csúcs és a γ szög található, mint a következő ábrán:

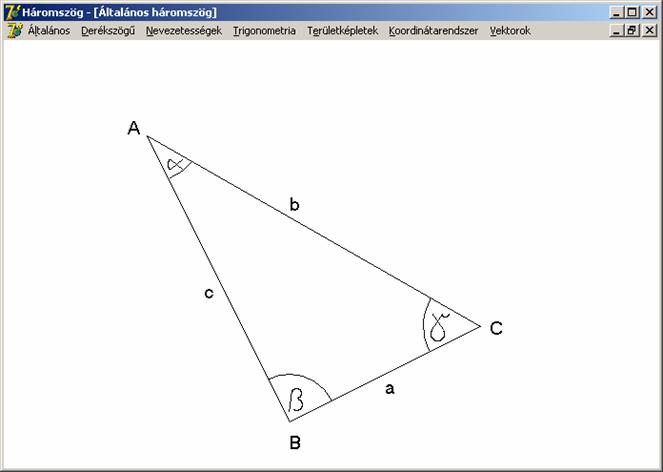
A háromszög oldalainak hosszát az oldalak nevével, a szögek nagyságát a szögek nevével azonosítjuk. Ha egy háromszög oldalairól és szögeiről semmilyen megkötés nem ismert, akkor általános háromszögről szoktunk beszélni. Az általános háromszögekre vonatkozó állítások természetesen bármely háromszögre (azaz a speciálisakra is) érvényesek. A továbbiakban, ha mást nem mondunk, mindig az Euklideszi geometriában érvényes állításokat fogalmazunk meg.

Alapvető tételek háromszögekre:

A háromszögek oldalai és szögei között a következő nagysági viszonyok figyelhetők meg:

- ha egy háromszögnek van két különböző oldala, akkor a nagyobb oldallal szemközt nagyobb szög található és viszont;

- vagy másképpen: kisebb oldallal szemközt kisebb szög található és viszont;

- azonos hosszúságú oldalakkal szemben azonos nagyságú szögek találhatók és viszont.

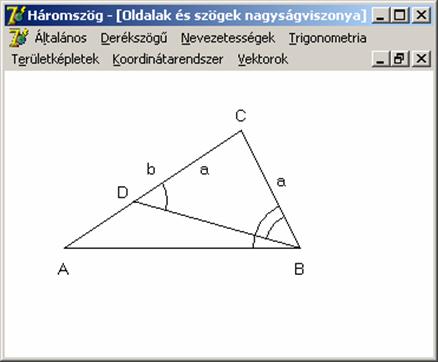
Az ábra szerint a BCD egyenlő szárú, azaz CB = CD = a, ezért DBC = BDC . De az ABC tartalmazza a BDC -et, így ABC > DBC . Az AC = b oldal viszont a CD = a-t tartalmazza, ezért b > a. Azaz a nagyobb oldallal szemben nagyobb szög található.

Igaz a következő: egy háromszög a oldala az A csúcsból látszik a legkisebb szög alatt a háromszögre eső (belső vagy kerületen lévő) pontok közül.

Minden háromszögre érvényes az úgynevezett háromszög-egyenlőtlenség, amely mint tétel azt mondja ki, hogy egy háromszögben bármely két oldal összege nagyobb, mint a harmadik oldal. Ugyanez különbséggel megfogalmazva: bármely két oldal különbsége kisebb a harmadiknál. Harmadik megfogalmazása ugyanennek: a háromszög fél-kerülete nagyobb, mint a háromszög bármely oldala. A háromszög-egyenlőtlenség tehát három egyenlőtlenséget jelent. Azaz:

1. a + b > c; a + c > b; b + c > a;

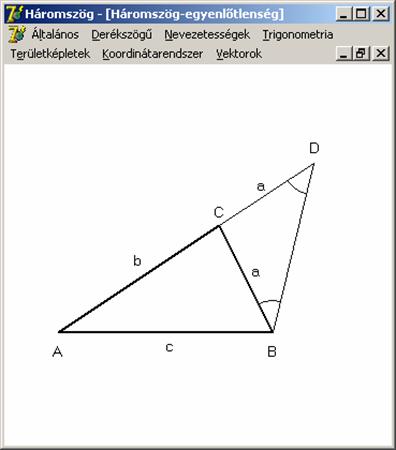
Az AC oldal meghosszabbításán felmértük az a oldalt, így a BDC háromszög egyenlő szárú, a jelölt szögei tehát egyenlők. Mivel a BC az ABD belsejében van, így ABD > CBD , azaz ABD > ADB . Tehát az ezekkel szemben lévő oldalakra is fennáll: AD > AB, azaz a + b > c.

2. átrendezve az előző egyenlőtlenségeket: a – b < c; a – c < b; b – c < a; vagy a fél-kerület segítségével:

3. ha s = (a + b + c)/2, akkor s > a; s > b; s > c.

Ez utóbbi visszavezetése az elsőre:

s > c

(a + b + c)/2 > c

a + b + c > 2c

a + b > c.

A tétel igazsága abból is adódik, hogy két pont között az Euklideszi geometriában a legrövidebb vonal az egyenes szakasz. Márpedig, ha A-ból a B-be az egyenes helyett egy töröttvonalon (például C csúcson keresztül) haladunk, akkor hosszabb utat kell megtennünk.

A háromszög belső szögeinek összege 180º. Ez a tétel az euklideszi párhuzamossági axiómával ekvivalens, annak egy átfogalmazása.

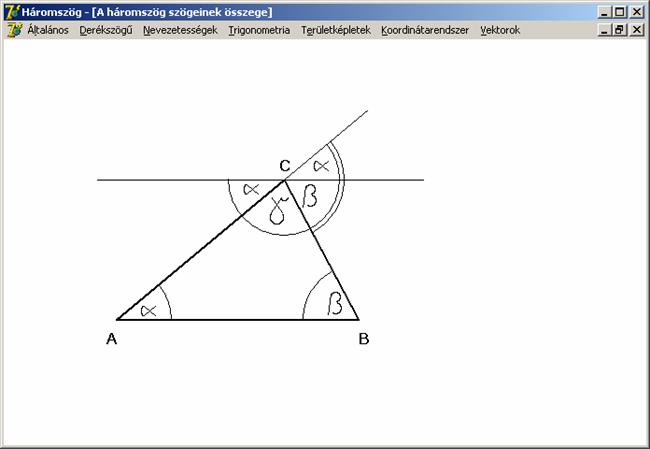
A rajzról jól látható, hogy az AB oldallal párhuzamos egyenesen a C csúcsnál található egyenesszög (váltószögek egyenlősége miatt) az ABC háromszög három szögéből tevődik összege, azaz a szögek összege 180º.

Egy háromszög külső szöge egyenlő a nem mellette lévő két belső szög összegével (ez is leolvasható az előző rajzról, ahol a kettős ívvel jelölt szög a C csúcsnál lévő külső szög és a két α szög azért egyenlő, mert csúcsszögek). Ez az előző tétel egyenes folyománya. Ezek alapján nyilvánvaló, hogy a háromszög bármely külső szöge nagyobb, mint egy nem mellette fekvő belső szög.

Mindebből az is következik, hogy a háromszög külső szögeinek összege 360º. Ugyanis a külső szögeket rendre összeadva: -ot kapunk.

A háromszög ugyanazon csúcsaihoz tartozó belső és külső szögfelezők merőlegesek egymásra.

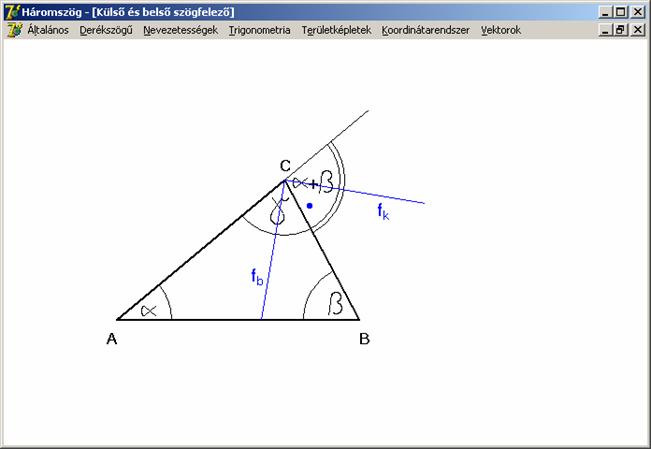
A rajzról a következő olvasható le, ahol a f_b a belső f_k pedig a külső szögfelező:

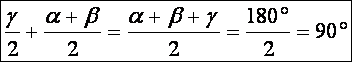
Következő lap: Vissza: http://gorbem.hu/MT/Haromszog2.htm