Differenciálgeometria (9)

Felületek

Már az előző lapokon is volt dolgunk felületekkel. Találkoztunk a síkkal, hengerrel, gömbbel, kúppal és különböző paraboloidokkal. Ezeknek a felületek a metszeteként állítottunk elő térbeli görbéket. Mindehhez meg kellett adni a felületeknek különböző egyenleteit. Ugyanakkor nem foglakoztunk a felületek belső tulajdonságaival. Ettől a laptól kezdve épp ez lesz a dolgunk. Ennek figyelembe vételével definiáljuk a felület fogalmát, majd megvizsgáljuk a felületek tulajdonságait.

A felületek definíciójánál megköveteljük, hogy a sík és a felület közötti kapcsolatot topológikus, azaz minkét irányban folytonos leképezés definiálja. Ugyanakkor a felületeket differenciálható függvényekkel szeretnénk leírni azért, hogy rajtuk felületi normálist és érintő síkot tudjunk definiálni. Először az elemi felület definícióját adjuk meg:

Elemi felületen egy olyan alakzatot értünk, amely előáll az paramétersík egy egyszeresen összefüggő tartományán értelmezett kétparaméteres vektorfüggvény helyvektorainak végpontjaiként, ha

1.) az által definiált leképezés topológikus,

2.) az folytonosan differenciálható és

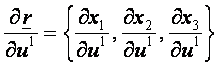3.) a és a 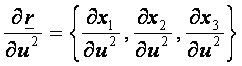vektorok sehol sem párhuzamosak.

Az elemi felület 1. – 3. tulajdonságú előállítását reguláris előállításnak nevezzük. Vannak olyan definíciók, amelyben a 3.) pontbeli párhuzamosságot véges sok helyen megengedik.

A felületeknek a fenti feltételeknek eleget tevő kétparaméteres megadási módját Gauss-féle megadási módnak nevezzük (én ezt leginkább egyszerűen csak paraméteresnek fogom nevezni). A felületek megadhatók még a z = f(x, y) explicit, és az F(x, y, z) = 0 implicit módon, melyet Euler-Monge-féle megadási módnak nevezünk. A paraméteres megadási módról egyszerű behelyettesítéssel áttérhetünk az F(x, y, z) = 0 Euler-Monge-féle megadási módra, és explicitről egyszerűen átrendezéssel kaphatunk implicitet. Ugyanakkor impicitről áttérni explicitre már gyakran csak elvileg lehetséges (például egy rögzített pont környezetében, ha ott a z szerinti parciális derivált nem nulla), de a gyakorlatban ez nem mindig egyszerű.

Most lássuk néhány felület különböző megadási módját. Az paraméterek helyett (u, v) paramétereket használunk (a könnyebb kezelhetőség miatt). A most következő felületek többségét már ábrázoltam (a Differenciálgeometria (7) lapon láthatók). Amelyeket még nem, azokat most ábrázolni is fogom.

Sík:

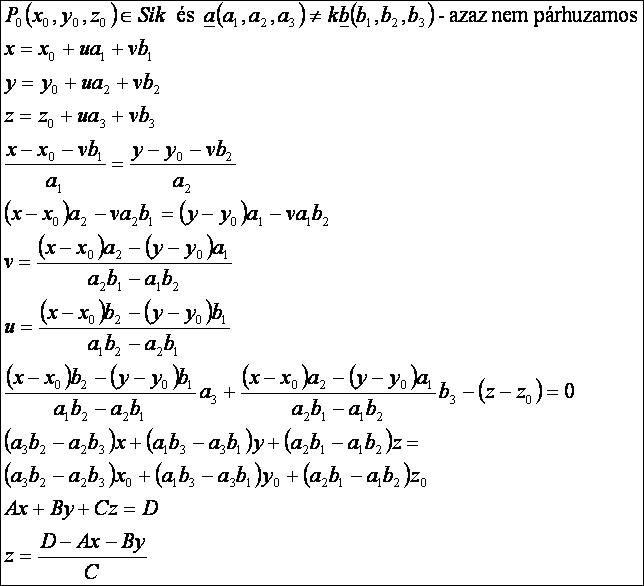
Jól látható, hogy a pont rajta van a síkon, hiszen kielégíti a sík egyenletét.

Gömb:

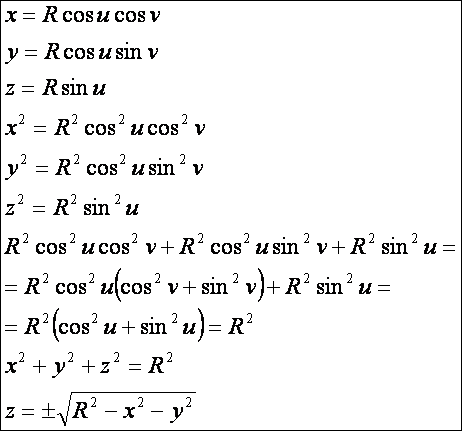
Ellipszoid:

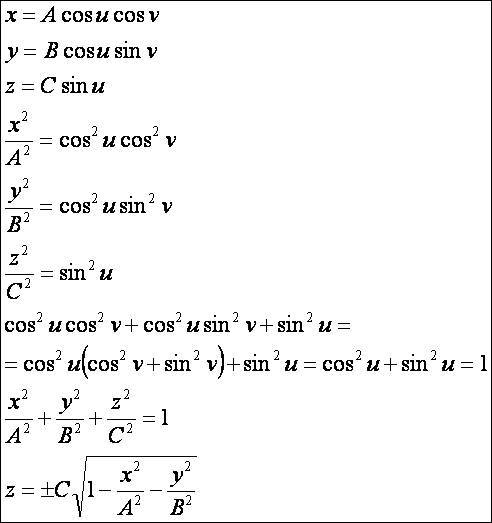
A gömb az ellipszoidnak A = B = C = R szerinti speciális esete.

Elliptikus paraboloid:

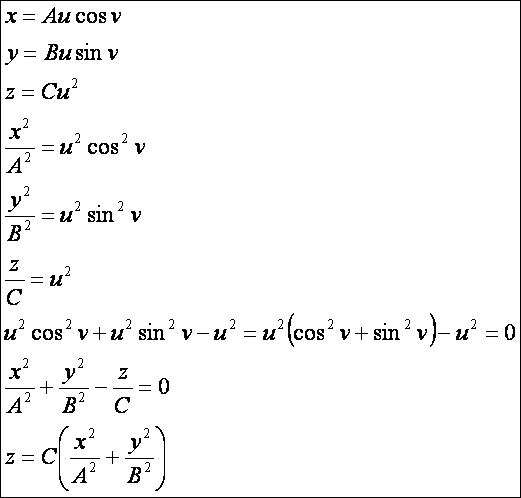
Ha az elliptikus paraboloid esetén A = B akkor forgásparaboloidot kapunk.

Elliptikus henger:

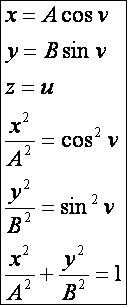
Ha az elliptikus henger esetén A = B akkor forgáshengert kapunk.

Elliptikus kúp:

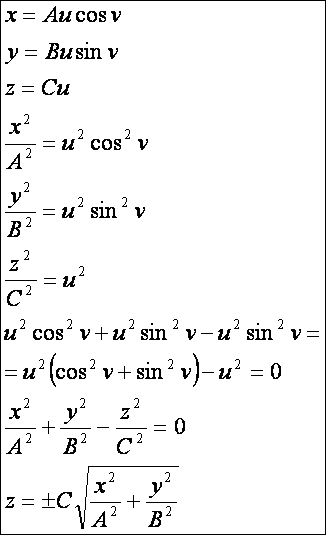
Ha az elliptikus kúp esetén A = B akkor forgáskúpot kapunk.

A következő paraméteres előállításban szükség lesz a hiperbolikus függvényekre. A szinusz hiperbolikusz és koszinusz hiperbolikusz definíciója:

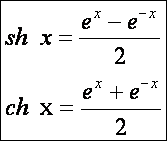
Egyköpenyű hiperboloid:

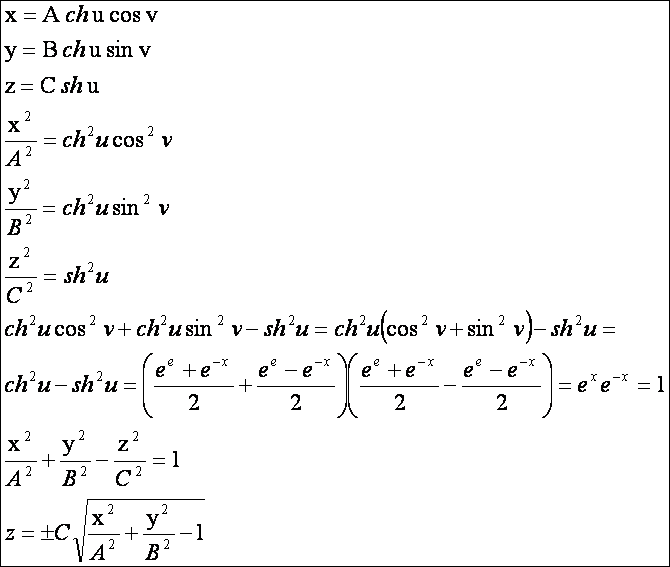
A = 0,8; B = 1,2; C = 1,6

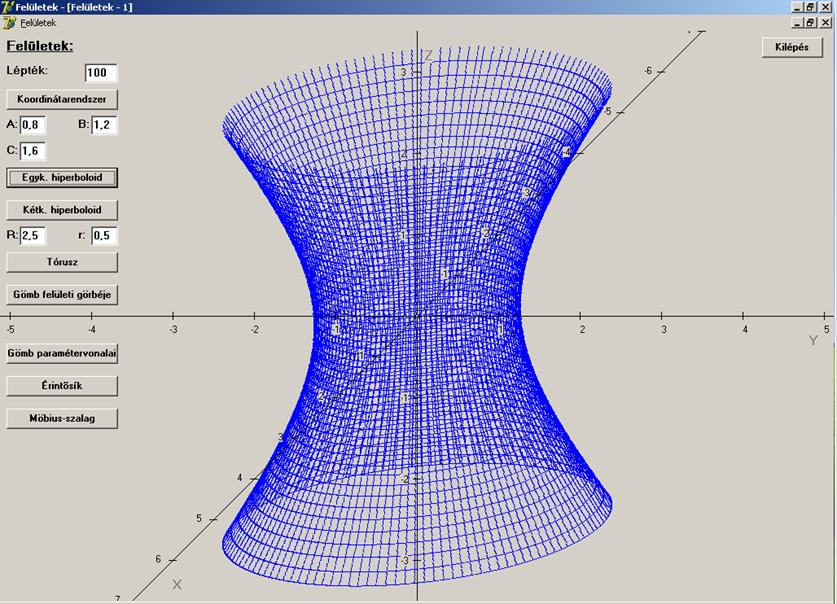
Ha az egyköpenyű hiperboloid esetén A = B, akkor egyköpenyű forgáshiperboloidot kapunk.

Kétköpenyű hiperboloid:

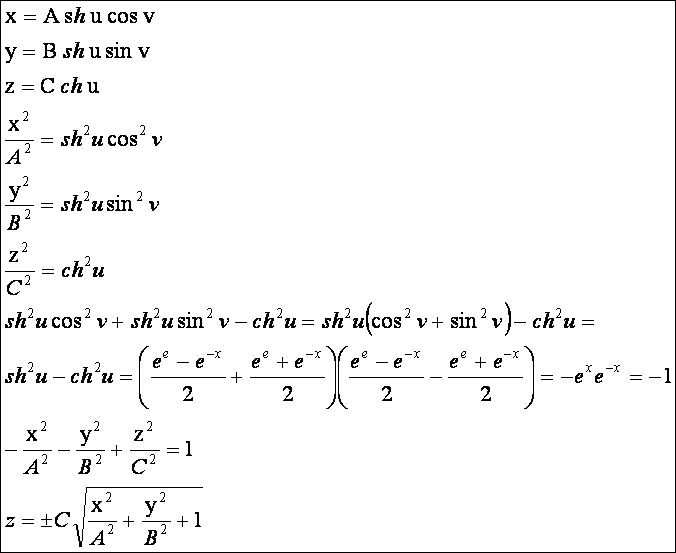
A = 0,4; B = 0,8; C = 1

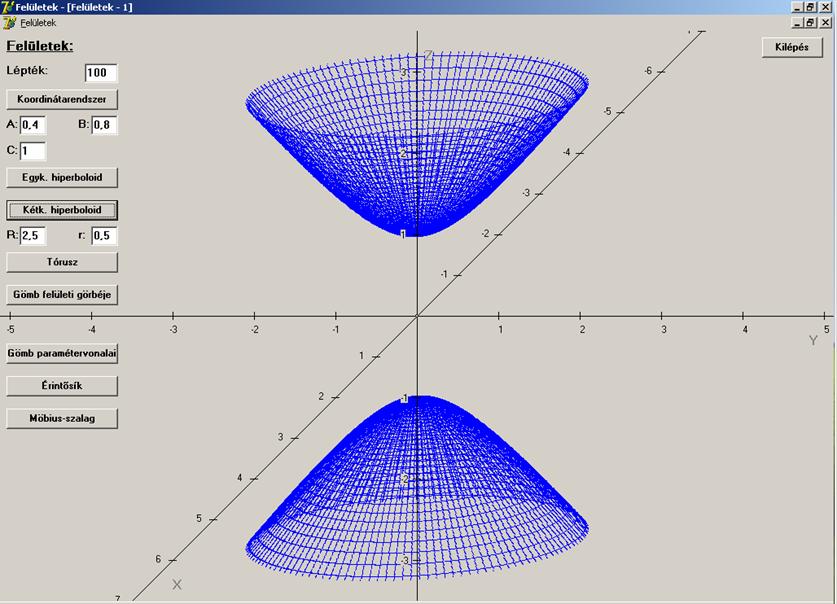
Ha a kétköpenyű hiperboloid esetén A = B, akkor kétköpenyű forgáshiperboloidot kapunk.

Hiperbolikus paraboloid:

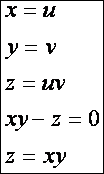
Tórusz:

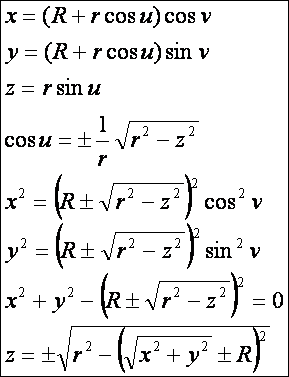
R = 2,5; r = 0,5

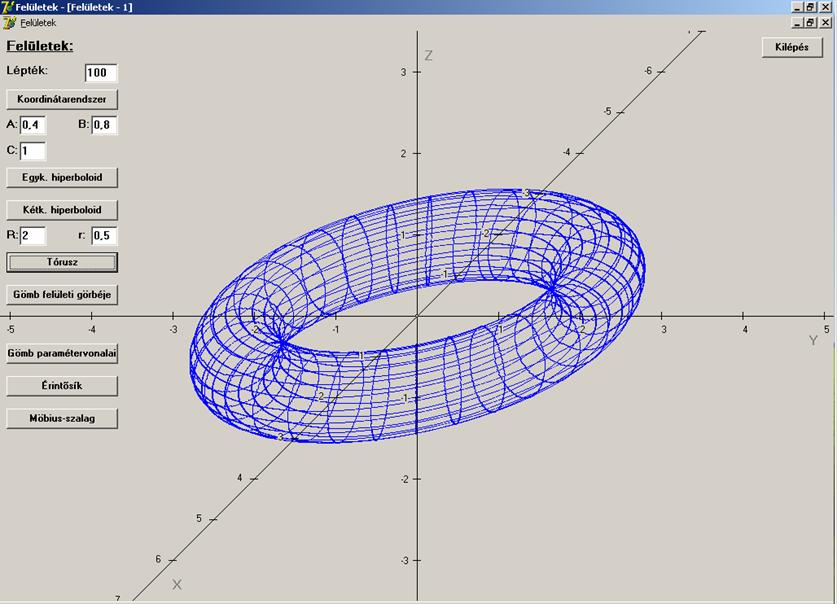
Ha példát szeretnénk mondani elemi felületekre, akkor nagyon óvatosnak kell lennünk, mert például a gömböt (teljes egészében) vagy a hengert (szintén teljes egészében) már el is felejthetjük. Ugyanis topológiából ismeretes, hogy a teljes gömbfelület nem homeomorf a sík egyetlen tartományával sem. Mivel a henger és a gömb viszont homeomorf, így a henger sem vetíthető folytonos leképezéssel a síkra. Ugyanez a helyzet a tórusszal is. Ezek tehát nem elemi felületek. A sík, a kúp és a paraboloid viszont már igen. Azért, hogy vizsgálatainkból ne zárjuk ki például az itt említett nem elemi felületeket, a felületet a következőképpen definiáljuk:

A felület a háromdimenziós euklideszi tér pontjainak olyan összefüggő halmaza, amely véges sok elemi felületdarab egyesítésével előállítható. A ponthalmaz összefüggő, ha bármely két pontja összeköthető olyan folytonos görbével, amelynek minden pontja ponthalmazhoz tartozik.

Nyilvánvaló, hogy például a gömb, a henger és a tórusz is előállítható véges sok elemi felület uniójaként, így beletartoznak a felületek halmazába.

Felület határpontja olyan pont, melynek bármely térbeli környezetében van a felülethez tartozó és felülethez nem tartozó pont is. A felület határán a határpontjainak halmazát értjük. Ha egy felületnek nincsenek határpontjai és véges, akkor zártnak nevezzük. Ilyen például a gömb vagy a tórusz. Ha egy felületnek vannak határpontjai vagy végtelen, akkor a felületet nyíltnak nevezzük. Ilyen például a kúp, vagy a sík. Az, hogy egy felület nyílt vagy zárt a felület globális tulajdonsága. Ahogy a görbeelméletben, úgy itt is, a különböző görbületek, érintő sík és normális a felület pontbeli tulajdonságai lesznek. Lesznek aztán olyan tulajdonságok, amelyek ezektől eltérően, egy pont környezetére vonatkoznak, ezeket lokális tulajdonságoknak fogjuk nevezni.

Egy felületet paraméteresen többféle módon előállíthatunk. Minden paraméteres előállítás (ha az 1. – 3. feltételnek eleget tesz), egyértelműen meghatároz egy felületet, de egy felület nem határozza meg a paraméteres előállítását. A felület egy adott paraméteres előállításáról egy másikra való áttérést akkor nevezünk megengedett paraméter-transzformációnak, ha a paraméterek közötti megfeleltetésre igaz, hogy topológikus, folytonosan differenciálható és az első parciális deriváltakból álló mátrix rangja 2. Azaz:

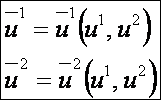
esetén a

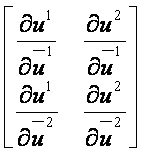
determináns értéke sehol sem nulla.

Ugyanazon felületnek tehát létezhet több különböző paraméteres előállítása. Például az elliptikus paraboloidnak – amint azt fentebb láthattuk – az egyik paraméteres egyenletrendszere:

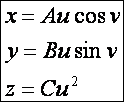
Mutassuk meg, hogy a következő paraméteres egyenletrendszer is elliptikus paraboloidot definiál:

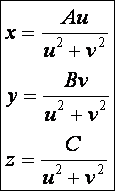
A bizonyítás:

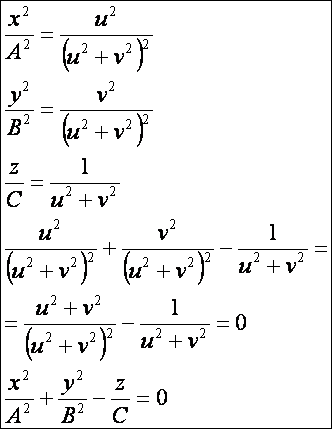
Lássunk még egy példát arra, hogy egy felületnek többféle paraméteres előállítása lehetséges. Mutassuk meg, hogy a

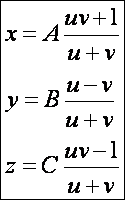
paraméteres egyenletrendszer is egyköpenyű hiperboloidot definiál. A bizonyítás:

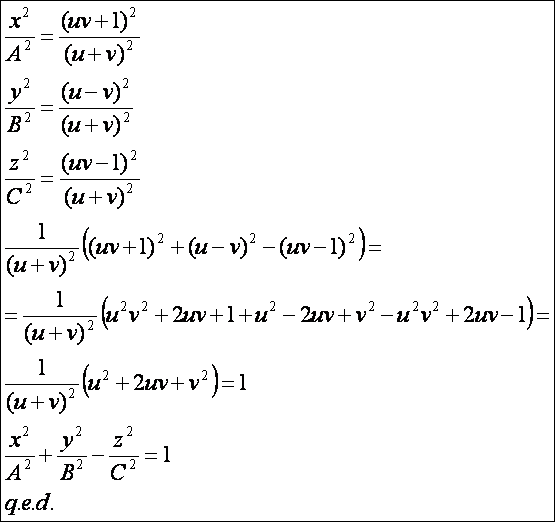
Felületi görbe, paramétervonal, érintősík, felületi normális

Ha az egy felület vektorparaméteres egyenlete, pedig a paramétersík egy görbéje, akkor az

az felület egy felületi görbéje. Lássunk erre egy példát a gömb felületén:

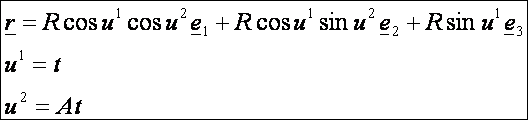
R = 2; A = 6

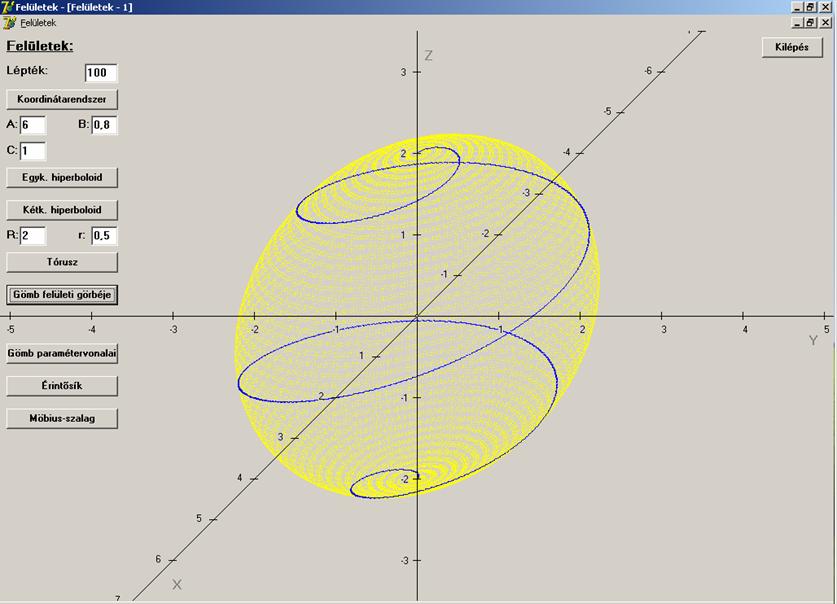
A felületi görbének abban a speciális esetében, amikor az egyik paraméter állandó, felületi paramétervonalakat kapunk. A felület mindkét paramétere szerint megadhatunk paramétervonalakat. Nézzünk ilyen paramétervonalakat a gömb esetén:

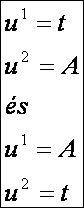
A = 1 … 5

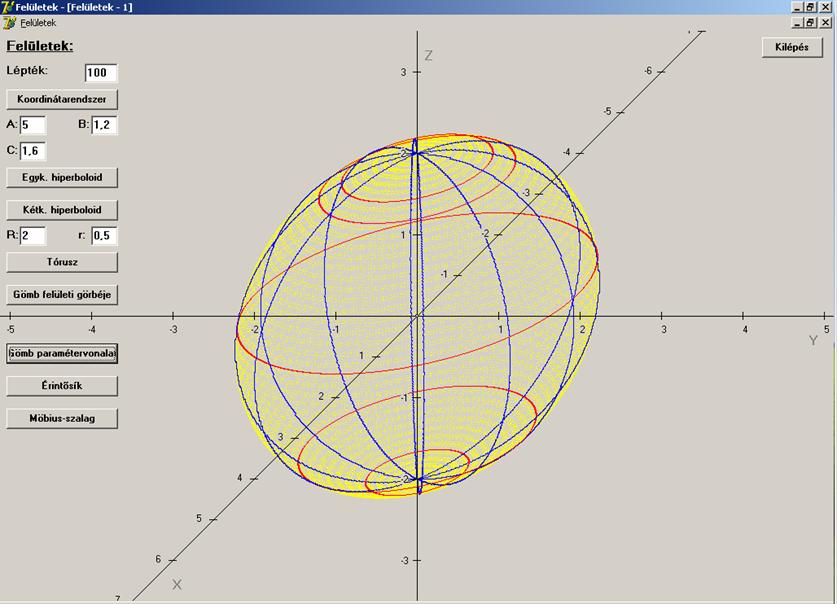
Jól látható, hogy a gömb fenti paraméterezésénél a paramétervonalak a gömb szélességi körei (piros színnel) és a hosszúsági főkörei (kék színnel), ahogy azt a Föld felületének ábrázolásából ismerjük. Általánosságban azt mondhatjuk, hogy ha a paramétervonalak állandóit külön-külön változtatjuk, akkor egy-egy paramétervonal sereget kapunk, mindkét paraméterre vonatkozóan. Ez a két paramétersereg egyrétegűen fedi le a felületet, azaz a felület bármely pontján összesen két paramétervonal megy át, melyek különböző paramétervonal sereghez tartoznak (a gömb fenti példájában az egyik a piros, a másik a kék sereghez).

Egy felület adott pontján átmenő és ebben a pontban differenciálható felületi görbék érintői valamennyien egy síkban vannak. Ezt a síkot a felület adott pontbeli érintősíkjának, a benne lévő vektorokat pedig felületi vektoroknak nevezzük. Az S(X, Y, Z) érintősík egyenlete az felület paraméterek által meghatározott P₀ pontjában:

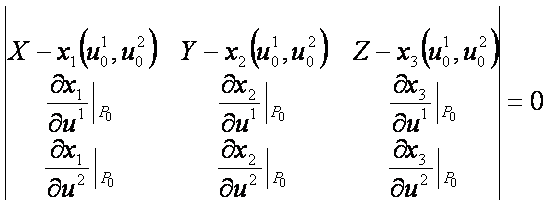
Az érintősíkot felfeszítő, paramétervonal-érintőkből képzett

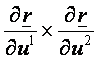
az érintősíkra merőleges vektort, a felület normálvektorának, az ilyen irányú egységvektort a felület normál-egységvektorának nevezzük, melyet -el jelölünk. Ennek segítségével az érintő sík egyenlete:

ahol az S a sík általános pontja, pedig a felület érintősíkkal közös pontja, az érintési pont. A felület normál-egységvektora a felület által nincs egyértelműen meghatározva. Ha például, a paraméterezésnél a két paramétert felcseréljük, akkor a normálvektor előjelet, azaz irányt vált. Ugyancsak ellentétes irányú vektort kapunk egyéb olyan megengedett paraméter-transzformáció után, ahol a

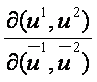
függvénydetermináns negatív.

Szemléltetésként rajzoljuk meg egy forgási paraboloid egy adott pontjában a paramétervonalakat, a paramétervonal-érintőket, az érintősíkot és a normálvektort. A paraboloid paraméteres egyenletrendszere:

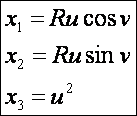
A paramétervonal-érintő vektorok összetevői:

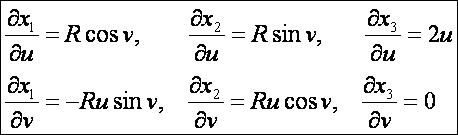
A normálvektor:

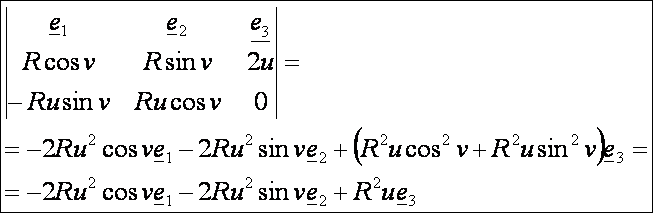
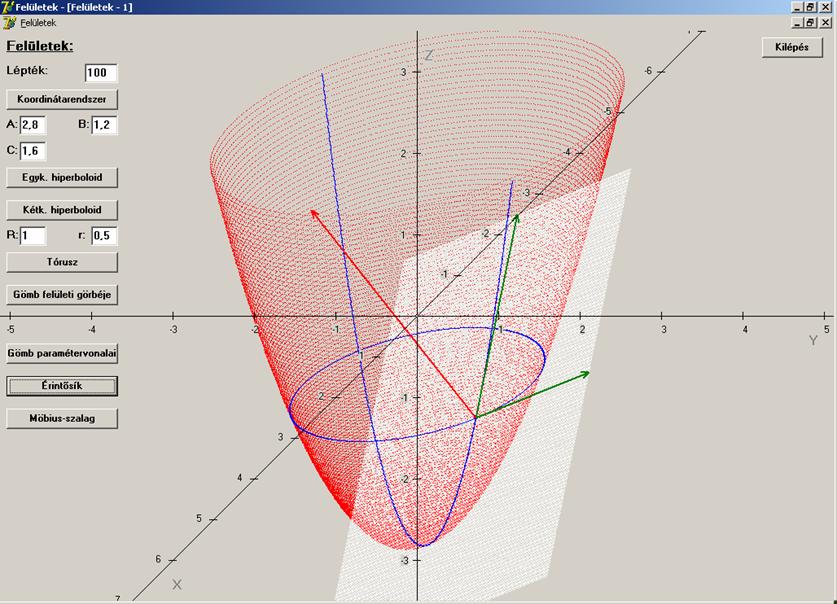
Ezek alapján a rajz (a paraboloid piros, a paramétervonalak kékek, a paramétervonal-érintők zöldek, normálvektor piros, az érintő sík pedig fehér):

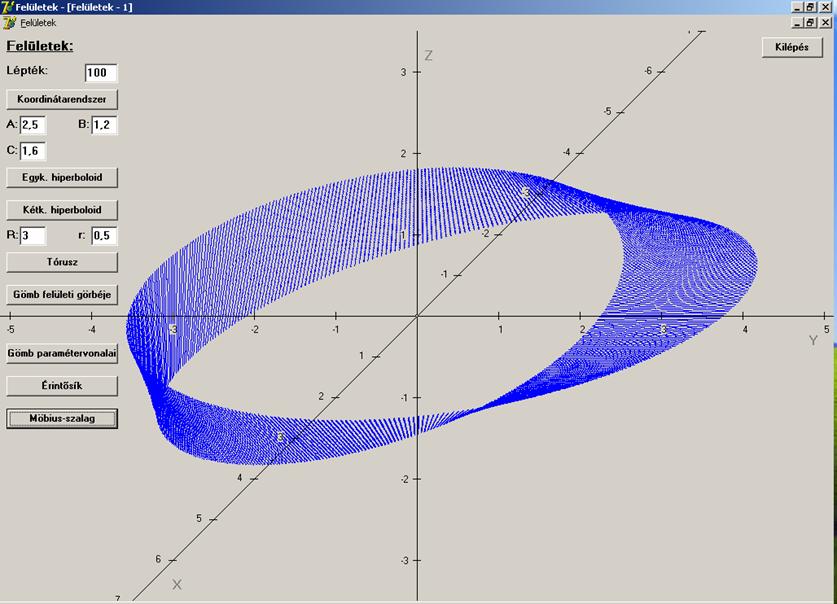
Ha a felületen értelmezhető egy normál-egységvektorokból álló folytonos vektormező (azaz a felület bármely pontjában adott egy vektor), akkor a felületet irányíthatónak (ha a vektormezőt megadjuk, akkor irányítottnak), ellenkező esetben a felületet nem irányíthatónak nevezzük. Minden elemi felület irányítható, de például a Möbius-szalag nem irányítható felület:

Következő lap: http://gorbem.hu/MT/DiffGeom10.htm