Differenciálgeometria (18)

Állandó Gauss görbületű felületek

Ha a felület egy adott pontjában a normálgörbület a normálmetszet síkjától (annak állásától) független (azaz minden irány főirány), akkor a két főnormálgörbület ugyanaz az érték, mivel azok a normálgörbület szélsőértékei. Ekkor a főnormálgörbület értéke szerint három eset lehetséges. Ha a főnormálgörbület 0, akkor az adott pontot síkpontnak, ha a főnormálgörbület pozitív, akkor gömbi pontnak, ha negatív, akkor hiperbolikus pontoknak nevezzük. Lehetséges olyan eset is, amikor a normálgörbület a felület minden pontjában ugyanaz. Mivel a Gauss görbület a főnormálgörbületek szorzata, az ilyen felületeket állandó Gauss görbületű felületeknek nevezzük. Nézzük, melyek ezek a felületek.

A sík

A sík paraméteres előállítása:

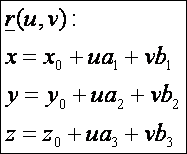
Az első deriváltak:

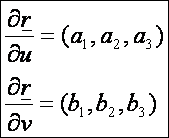
Az első alapmennyiségek:

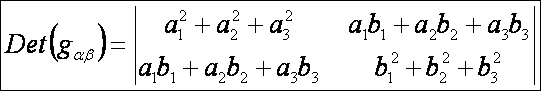
A második alapmennyiségek (DiffGeom14.htm alapján):

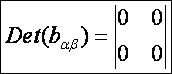
A főnormálgörbületek:

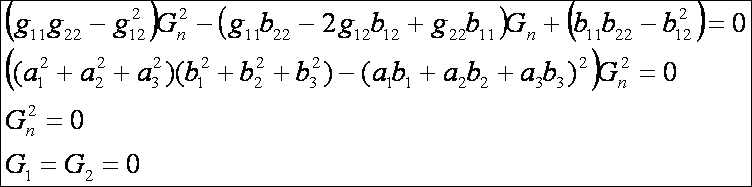
A Gauss görbület:

A Minkowski görbület:

A sík tehát állandó Gauss görbületű felület, melynek a Minkowski görbülete is állandó.

A gömb

A gömb paraméteres egyenletrendszere:

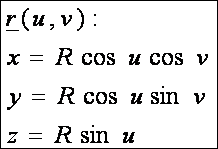
Az első alapmennyiségek (DiffGeom11.htm alapján):

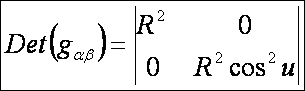
A második alapmennyiségek (DiffGeom14.htm alapján):

A főnormálgörbületek (DiffGeom15.htm alapján):

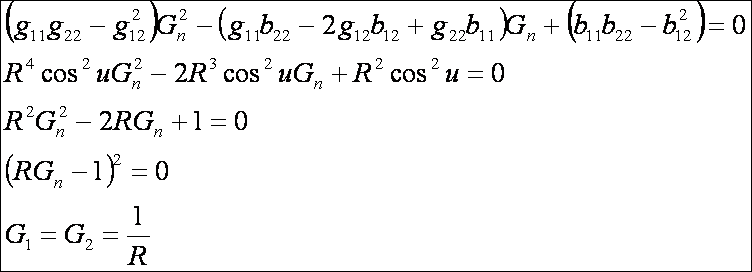
A Gauss görbület:

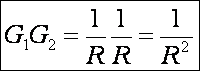
A Minkowski görbület:

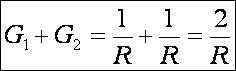
A gömb tehát egy állandó Gauss görbületű felület, melynek a Minkowski görbülete is állandó.

A pszeudoszféra

A pszeudoszféra paraméteres egyenletrendszere:

Az első alapmennyiségek. Mivel:

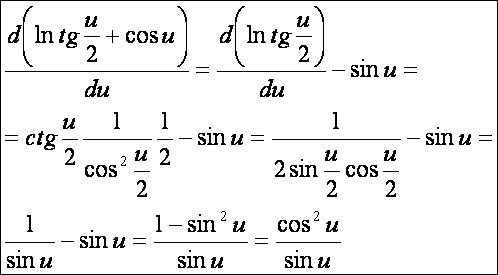
Így:

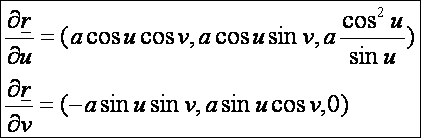
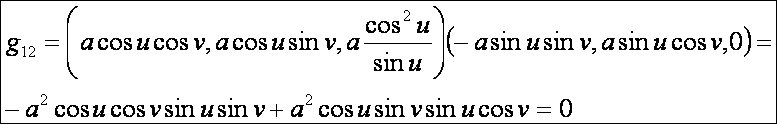
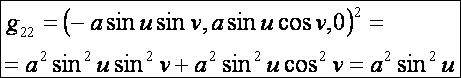
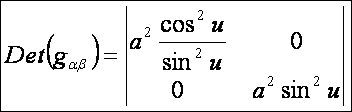
A felület normálvektora:

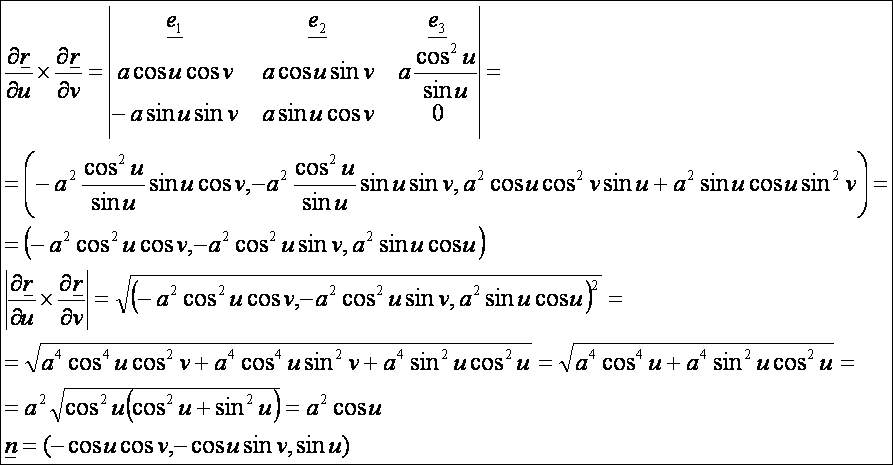
A második deriváltak:

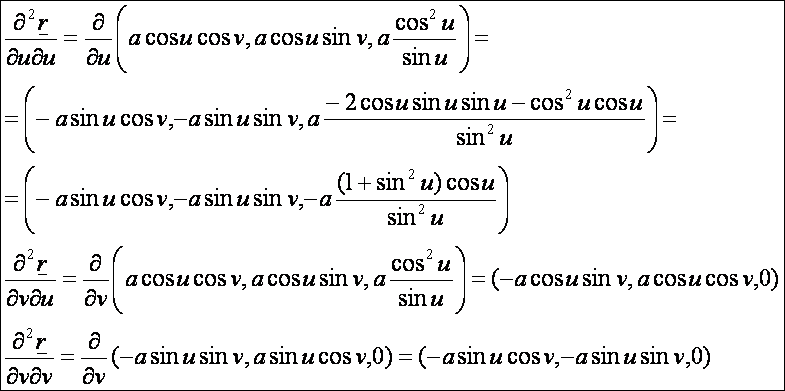
Második alapmennyiségek:

Tehát a főnormálgörbületek:

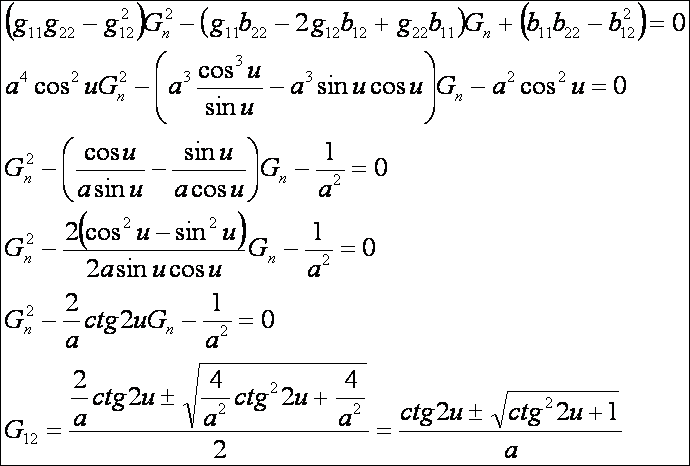
A Gauss görbület:

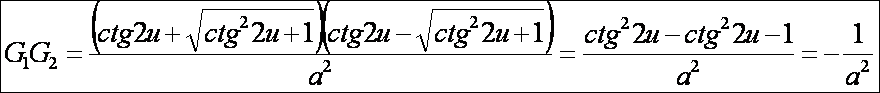
A Minkowski görbület:

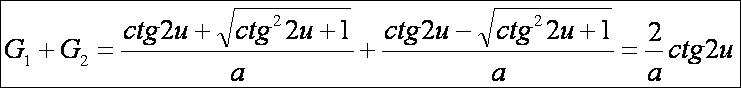
Ez utóbbi két görbület természetesen a

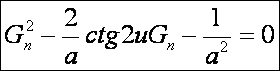
egyenlet együtthatóiból közvetlenül is kiolvasható (másodfokú egyenletek: gyökök és együtthatók közötti összefüggés).

A pszeudoszféra tehát egy állandó, mégpedig negatív állandó Gauss görbületű felület.

Így három állandó Gauss görbületű felületünk van: a sík, a gömb és a pszeudoszféra, melyek görbülete rendre: 0, 1/R² és -1/a². Minkowski görbület szerint viszont csak a sík és a gömb állandó görbületű, mert a pszeudoszféra esetén a Minkowski görbület már paraméterfüggő.

Néhány további felület Gauss és Minkowski görbülete

A henger

Az első alapmennyiségek (DiffGeom15.htm alapján):

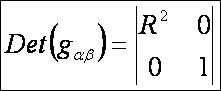
A második alapmennyiségek:

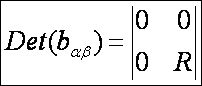
Ezek alapján a főnormálgörbületek:

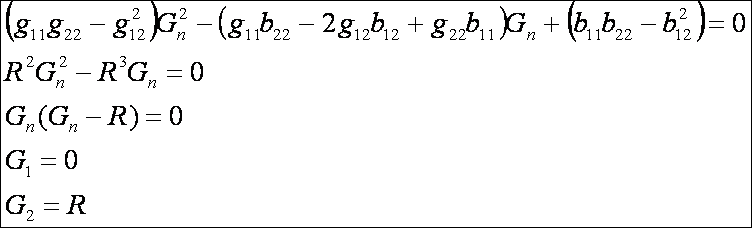
A Gauss görbület:

A Minkowski görbület:

A kúp

Az első alapmennyiségek (DiffGeom15.htm alapján):

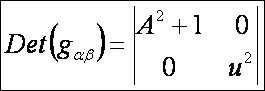
A második alapmennyiségek:

Ezek alapján a főnormálgörbületek:

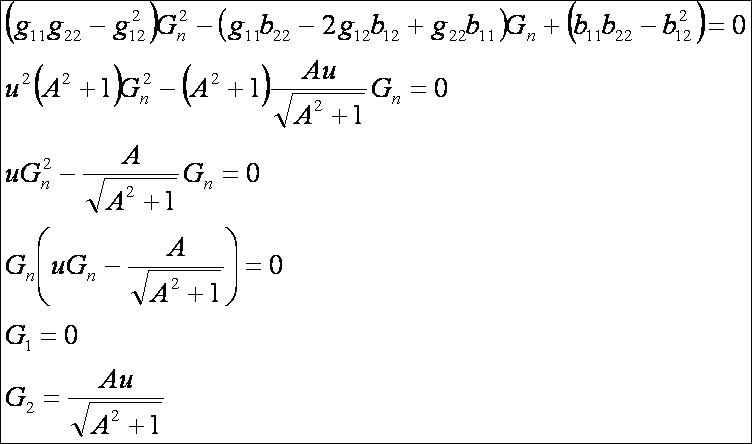
A Gauss görbület:

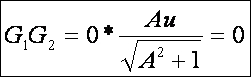
A Minkowski görbület:

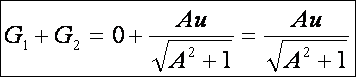
A kúpnak és a hengernek is nulla a Gauss görbülete a felület minden pontjában, azaz ezek is állandó Gauss görbületű felületek. Konstans görbületűnek ettől még nem nevezném őket, mert minkét felület minden pontjában van nullától különböző főnormálgörbülete. Ugyanakkor mindkét felület minden pontja síkpont, mivel mindenütt nulla a Gauss görbülete. Nem véletlen a síkpont elnevezés, hiszen ezek a felületek síkba fejthetők, ugyanaz a belső geometriájuk. Azaz izometrikus leképezés létezik a kúp és a sík, illetve a henger és a sík között, de ebből adódóan a kúp és a henger között is (alkotóikkal összeillesztve egymásra fejthetők természetesen egy másik alkotójuk mentén fel kell vágni a felületeket).

Az egyenes csavarfelület

Az egyenes csavarfelület paraméteres előállítása:

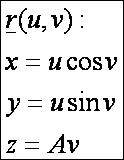
Az első alapmennyiségek:

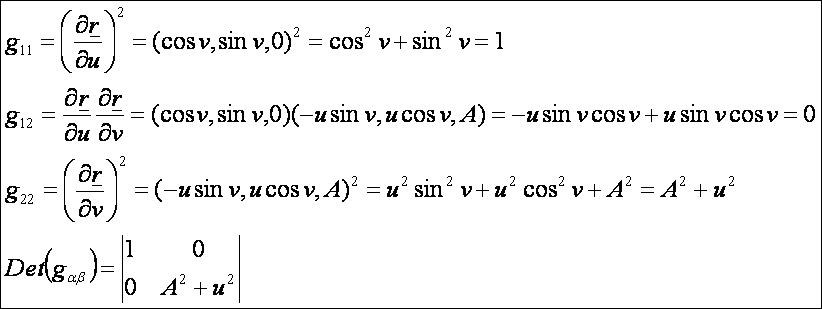
A második alapmennyiségek (DiffGeom14.htm alapján):

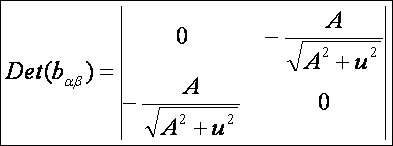
Ezek alapján a főnormálgörbületek:

A Gauss görbület:

A Minkowski görbület:

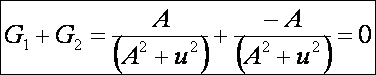
Az egyenes csavarfelületnek a Minnkowski görbülete nulla.

A tórusz

A tórusz paraméteres egyenletrendszer:

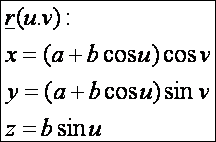
Az első alapmennyiségek (DiffGeom13.htm alapján):

Első deriváltak:

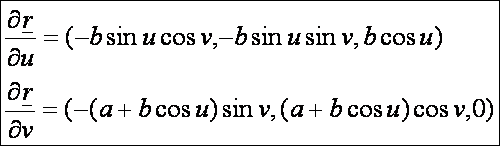
A felület normálvektora:

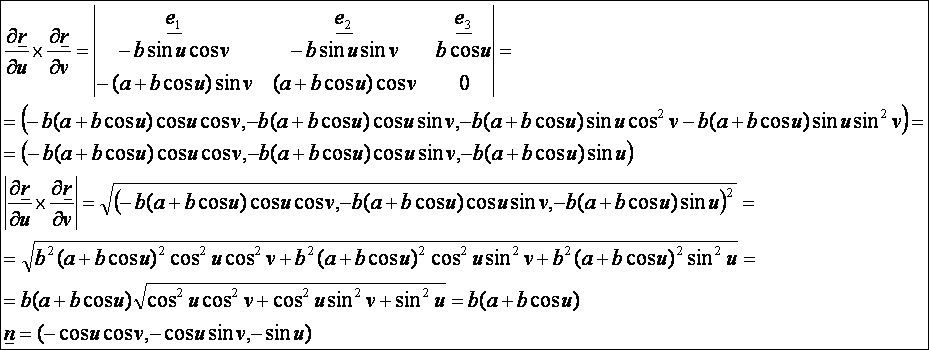
Második deriváltak:

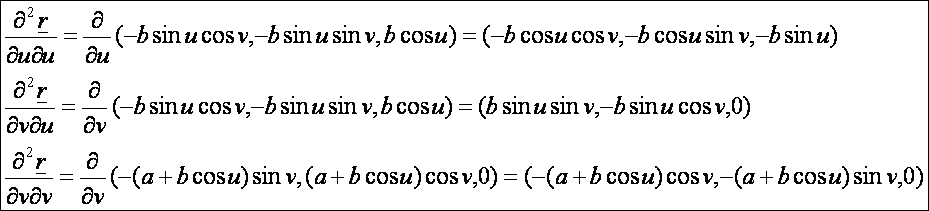
Második alapmennyiségek:

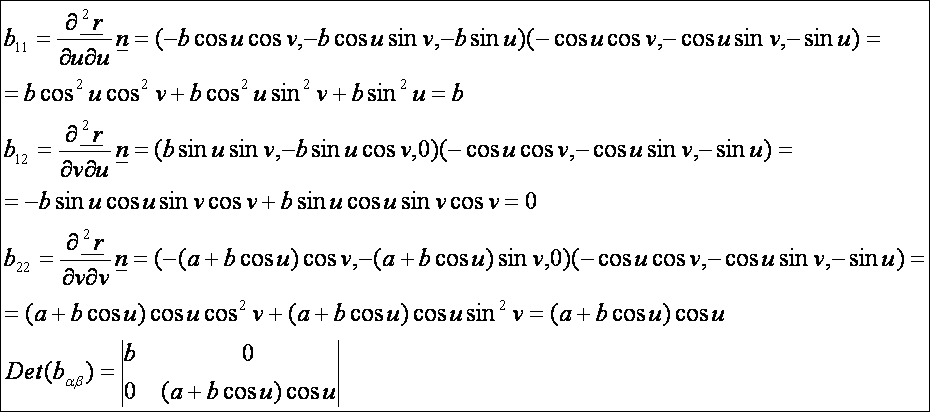
Ezek alapján a főnormálgörbületek:

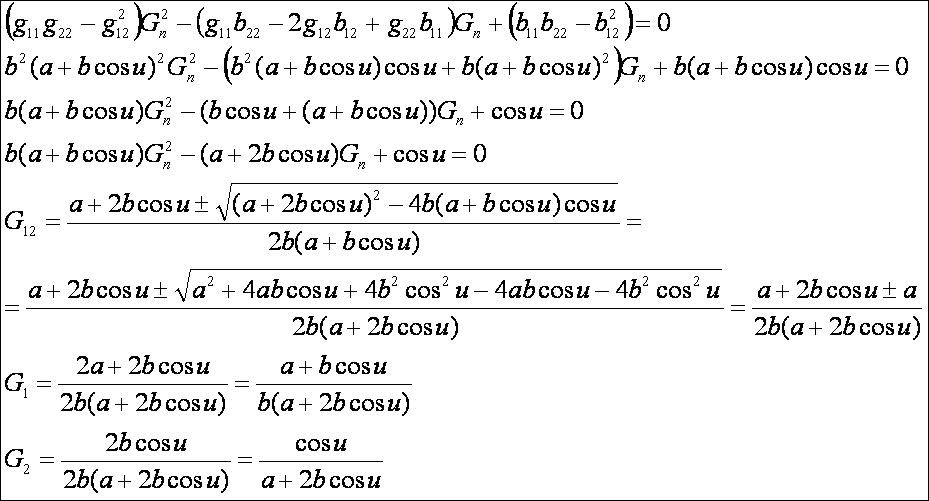
A Gauss görbület:

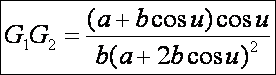
A Minkowski görbület:

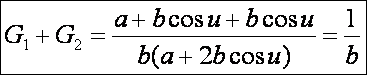
A tórusz is egy állandó Minkowski görbületű felület. A tórusz Gauss görbülete pedig csak az egyik paramétertől függ, mégpedig attól, amelyhez tartozó u paramétervonalak a b(<a) sugarú testet körbefutják (kis körök). A teljes gyűrűt körbejáró v paramétervonalak mentén a görbületek állandók. A DiffGeom15.htm lapon a Dupin-féle indikátrix fejezetben, ábrázoltam a tórusz felületi pontjait, típusok szerinti jelölésekkel. Fekete a parabolikus, a fehér az elliptikus és a sárgával jelöltek a hiperbolikus pontok. Ez az osztályozás a most meghatározott Gauss görbületből is megállapítható. A Gauss görbület előjele ugyanis a cos u rész előjelével egyezik meg. Például a cos u = 0 esetén a fekete színű pontokat adja, mely a gyűrűn körbefutó két kör.

A katenoid

A kateonid paraméteres egyenletrendszere:

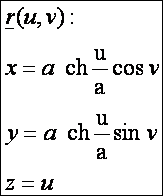
Első alapmennyiségek:

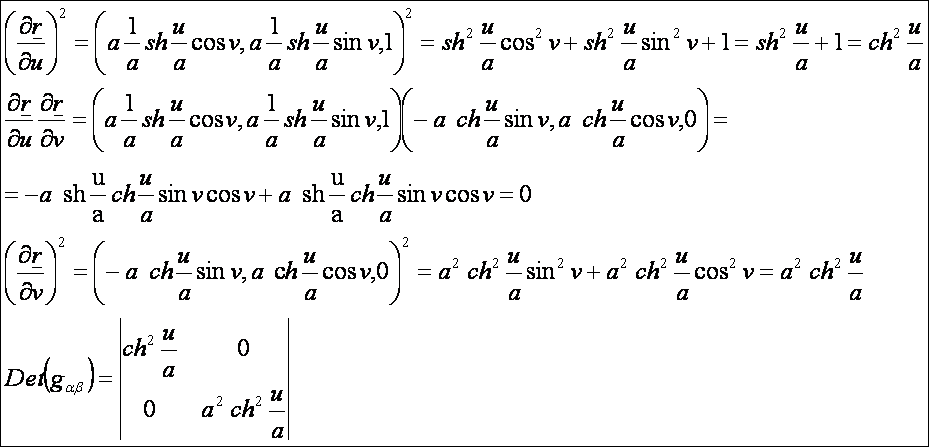
Második alapmennyiségek (DiffGeom14.htm alapján):

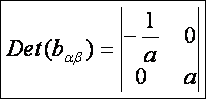
Ezek alapján a főnormálgörbületek:

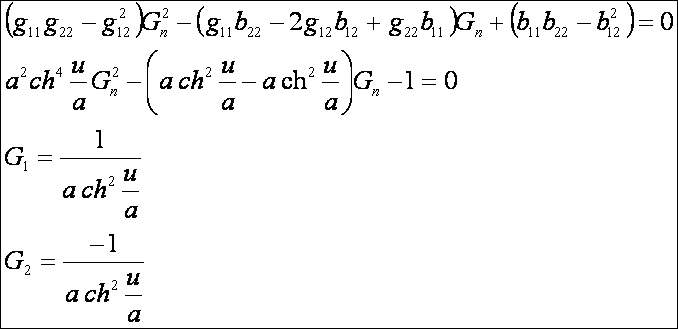
A Gauss görbület:

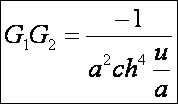
A Minkowski görbület:

A katenoid szintén egy konstans Minkowski görbületű felület, sőt ez a görbülete nulla.

A forgásparaboloid

Az forgásparaboloid paraméteres előállítása:

Az első alapmennyiségek (DiffGeom11.htm alapján, A = B = C = 1):

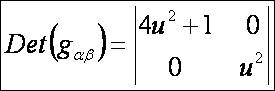
A második alapmennyiségek (DiffGeom11.htm alapján):

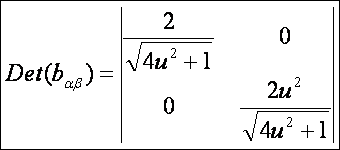
Ezek alapján a főnormálgörbületek:

A Gauss görbület:

A Minkowski görbület:

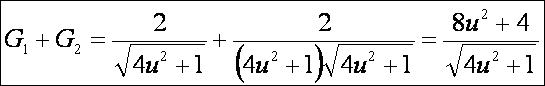
A hiperbolikus paraboloid

A hiperbolikus paraboloid paraméteres előállítása:

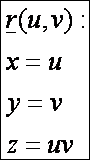
Az első deriváltak:

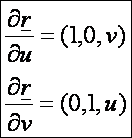
Az első alapmennyiségek:

A második alapmennyiségek (DiffGeom14.htm alapján):

Ezek alapján a főnormálgörbületek:

A Gauss görbület:

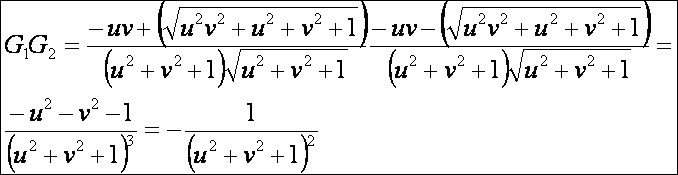
A Minkowski görbület:

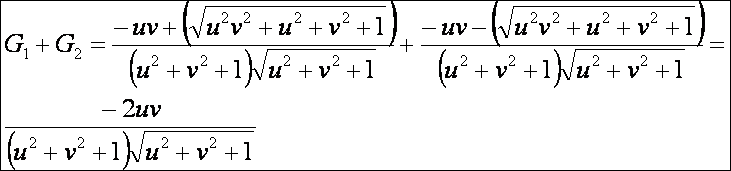
Theorema egregium

A Theorema Egregium (azaz Nevezetes Tétel) a differenciálgeometria fontos alaptétele, amely kimondja, hogy egy felület Gauss-görbülete csak a felület első alapmennyiségeitől függ. Azaz: a felület Gauss-görbületét meghatározza a felület metrikája (az, hogy a felületen hogyan mérünk szöget, illetve távolságot), és ez független a felület térbeli alakjától (amit viszont a második alapmennyiségek írnak le). Ez koránt sem nyilvánvaló, mert a felület főnormálgörbületei (amelyek szorzata a Gauss görbület) viszont függenek a második alapmennyiségektől. Mivel az első alapmennyiségek izometriával szemben invariánsak, ezért a tétel értelmében a Gauss-görbület is. Mint azt fentebb is láttuk, a gömb konstans pozitív Gauss-görbületű felület, míg a sík Gauss-görbülete minden pontban nulla. Ebből az következik, hogy ez a két felület nem képezhető le egymásra izometrikusan. Vagyis például nem készíthető távolságtartó térkép a Földről. Készíthető viszont szögtartó térkép, melyet a légi és vízi közlekedésben ma is használnak.

Következő lap: http://gorbem.hu/MT/DiffGeom19.htm