Differenciálgeometria (17)

Az Euler-Lagrange-féle differenciálegyenletek

A felületi görbék görbületének további vizsgálatához a sík egyenesinek analógiáját fogjuk megkeresni a felületeken. A sík két pontja között a legrövidebb görbe az egyenes szakasz. Tegyük fel ezt a kérdést a felületi görbékre vonatkozóan is. Azaz: egy adott felület két pontja között vajon melyik a legrövidebb felületi görbe? Nyilvánvaló, hogy a következő integrál minimumát kellene meghatározni, ahol az ismeretlen az u(t) felületi görbe.

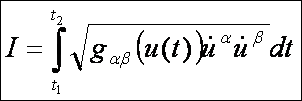
Olyan függvényeket, amelyek függvényeken vannak értelmezve funkcionáloknak nevezzük. Ezek alapján ez az integrál egy funkcionál. A matematikának azt az ágát, amely funkcionálok (vagy éppen az ilyen integrálok) szélsőértékét-számításával foglalkozik, variációszámításnak nevezzük. Most tehát következzen egy kis variációszámítás.

Jelölje az a tér egy függvényét, az pedig a deriváltját. Legyen adva egy hatváltozós, kétszer folytonosan deriválható függvény, továbbá legyen x₁ és x₂ két vektor. Keressük az x(t₁) = x₁ és x(t₂) = x₂ peremfeltételeket kielégítő x = x(t) görbéket, amelyek az

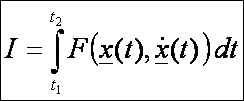
integrál szélsőértékeit adják. Egyáltalán nem biztos, hogy létezik a szélsőértéket megadó görbe. Ha az integrál ívhosszat határoz meg, akkor például nincs maximumot adó görbe. Ha létezik szélsőértéket megadó görbe, akkor pedig nem biztos, hogy az egyértelmű. Mert például a gömb felületén, annak két átellenes pontja között, minden e két ponton átmenő főkör minimális ívhosszat ad meg. A szélsőérték létezésének szükséges feltétele:

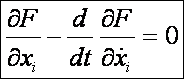
amely egy közönséges, másodrendű differenciálegyenlet-rendszer. Ezeket az egyenleteket a variációszámítás Euler-Lagrange-féle differenciálegyenleteinek, a benne szerepfő F függvényt alapfüggvénynek (esetleg alkotófüggvénynek) nevezzük. Az Euler-Lagrange-féle differenciálegyenlet megoldásai a stacionárius görbék. Ehhez a feltételi differenciálegyenlet-rendszerhez úgy juthatunk, hogy az megoldásgörbét egy, a fenti peremfeltételeket (a(t₁) = 0 és a(t₂) = 0) kielégítő görbesereg elemeként írjuk fel:

ahol a második tag az függvény variációját jelenti. A görbesereg elemei (elég kicsiny esetén) az környezetében helyezkednek el. A differenciálegyenletet kielégítő függvénynél ez a variáció eltűnik (mint a függvények szélsőértékénél, ahol a szükséges feltétel az első derivált eltűnése). Innen kapta a matematika ezen ága a variációszámítás elnevezést.

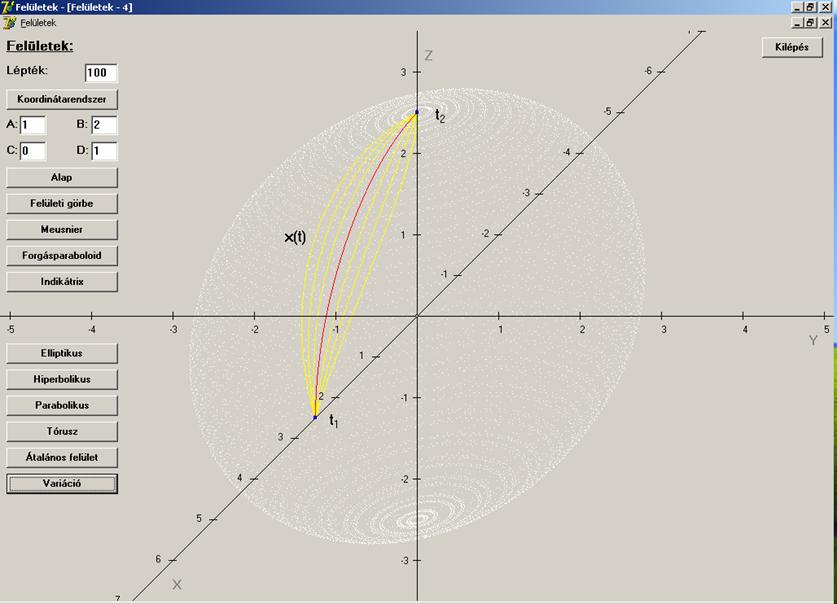
A következő ábrán a fentebbi görbesereg néhány elemét ábrázoltuk. Mindegyik eleme átmegy a peremfeltételi pontokon. A stacionárius görbe piros színű, a többit sárgával rajzoltuk. (Az egyszerűség kedvéért a görbék egy gömbfelületen vannak ábrázolva. Mivel csak a szemléltetés volt a cél, így ez az általánosság rovására nem ment, hiszen ez hasonlóan nézne ki bármely felület elég kicsiny darabján.)

Nézzük tehát, hogyan kaphatjuk meg a fenti, Euler-Lagrange-féle differenciálegyenleteket. Az integrálok értéke a fenti görbeseregre az függvénye:

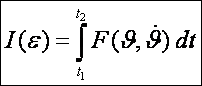
Ennek az helyen szélsőértéke van:

Vegyük az I szerinti deriváltját:

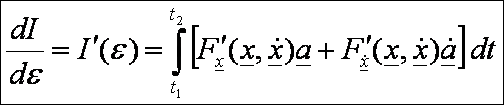
Ebben a kifejezésben:

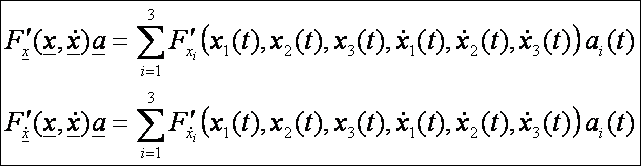
Így:

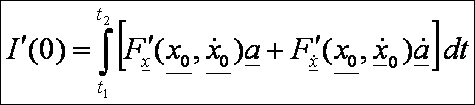
Parciálisan integrálva a második tagot:

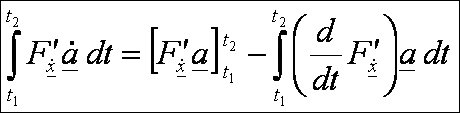
Mivel a(t₁) = a(t₂) = 0, így rendezés után ezt kapjuk:

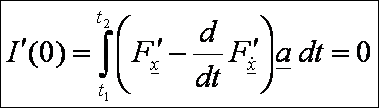
Ez viszont csak úgy lehetséges, ha:

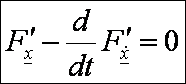
Ami nem más, mint a fentebbi Euler-Lagrange-féle differenciálegyenletek.

Említsünk meg itt néhány klasszikus variációszámítási feladatot, illetve problémát.

1. Két pont között legrövidebb görbe: Legyen adva a síkon két pont: P₁(x₁, y₁) és P₂(x₂, y₂), ahol x₁<x₂. Tekintsük azokat a folytonosan deriválható y = y(x) függvényeket, amelyek görbéi e két pontra illeszkednek. Melyik görbe ívhossza a legkisebb. A pontokat összekötő görbe ívhossza nyilván:

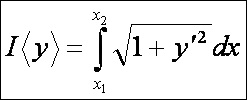
Elemi geometriából jól tudjuk, hogy ennek a feladatnak a megoldása a két pontot összekötő egyenes. Ennek egyenlete pedig:

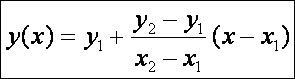
2. Brachisztochron-probléma: adva van a gravitációs térben két, nem azonos magasságban és nem egy függőleges egyenesre eső P₁(x₁, y₁) és P₂(x₂, y₂) pont, ahol x₁< x₂ és y₁> y₂. A nehézségi erő hatására mozgó anyagi pont a felső pontból az alsóba egy y = y(x) görbe mentén mozog, amely kényszerként hat a pontra és y(x₁) = y₁, valamint y(x₂) = y₂. Határozzuk meg a görbét úgy, hogy a mozgás a lehető legrövidebb idő alatt történjen meg. A sebességet a v = ds/dt derivált adja. Ebből dt = ds/v. A pályán való mozgás ideje tehát:

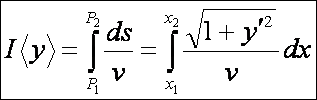
Az energia megmaradás törvénye szerint (a mozgási energia növekedése egyenlő a gravitációs energia csökkenésével, v₁ a kezdősebesség a P₁ pontban és g a gravitációs gyorsulás):

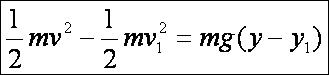
Ebből:

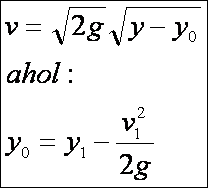
Így a pálya befutásához szükséges idő:

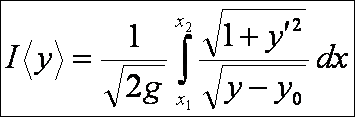
A brachisztrochon-probléma megoldása a ciklois, melynek paraméteres egyenletrendszere (a a peremfeltételekből meghatározandó álladó):

3. A legkisebb felszínű forgásfelület problémája: Legyen adva két P₁(x₁, y₁) és P₂(x₂, y₂) pont, ahol x₁<x₂, y₁>0 és y₂>0. Haladjon át a pontokon egy y = y(x) görbe, melynek a pontok közé eső részét megforgatjuk az x tengely körül. Legyen az y(x) az (x₁, x₂) intervallumon nem negatív. Ekkor a keletkező forgásfelület felszíne:

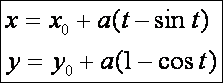
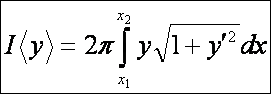
Határozzuk meg azt a görbét, amelyre a keletkezett forgásfelület felülete a legkisebb lesz. Ennek a problémának a megoldása a koszinusz hiperbolikus függvény:

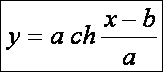
Itt az a és b a peremfeltételekből meghatározandó állandók.

A geodetikus vonal

A felületi görbék ívhosszának variációjánál a stacionárius görbéket geodetikus vonalaknak nevezzük. A feladatunk az lesz, hogy írjuk fel a geodetikus vonalak egyenletét ívhossz-paraméterben. Azaz legyen az Euler-Lagrange-féle differenciálegyenlet-rendszer alapfüggvénye:

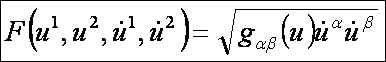
A Euler-Lagrange-féle differenciálegyenlet-rendszer:

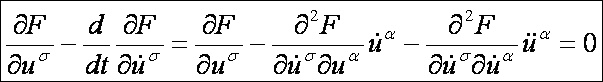
Számítsuk ki a jobboldali részeket az F alapfüggvényt segítségével. Az első deriváltak:

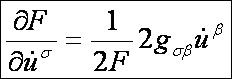
A második deriváltak:

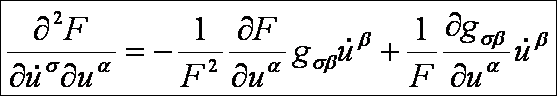
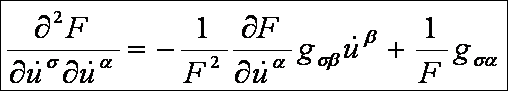
Ezek alapján az Euler-Lagrange-féle differenciálegyenlet-rendszer:

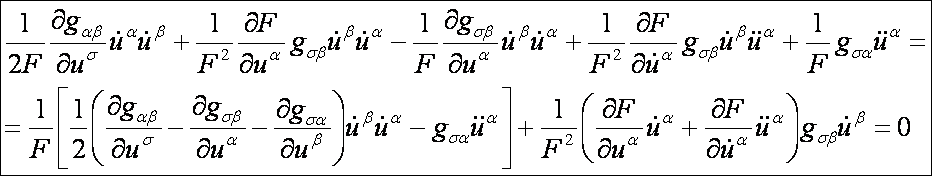
Mivel

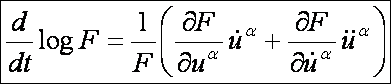
az elsőfajú Christoffel-féle szimbólumok segítségével az egyenletrendszer ilyen alakú:

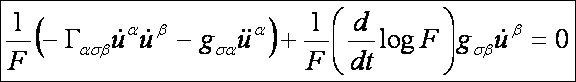
Vagyis:

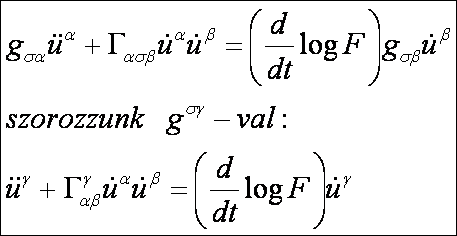
Most tekintsük az ívhosszat paraméternek, azaz:

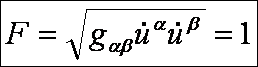
Így a geodetikus vonal egyenlete ívhossz-paraméterben:

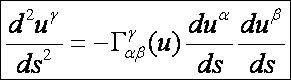
Most nézzünk néhány tulajdonságát a geodetikus vonalaknak.

Először is a geodetikus vonal egyenlete egy másodrendű differenciálegyenlet-rendszer. A peremfeltételekben azt adjuk meg, hogy mely pontból és milyen irányba induljon ki a geodetikus vonal. Ez az egyenletrendszer mindig egyetlen görbét ad megoldásul, azaz a felület minden pontjából, minden irányba egyetlen geodetikus indul ki.

Másodszor: két felületi pontot összekötő legrövidebb felületi görbe mindig geodetikus. Ugyanakkor ez fordítva nem feltétlen igaz. Például a henger felületén, ha a két pont nem azonos magasságban van, akkor köztük végtelen sok geodetikus húzható (ezek a hengeres csavarvonalak), de ebből csak egy a legrövidebb.

Harmadszor: sík esetén a másodfajú Christoffel-féle szimbólumok értékei nullák, így a differenciálegyenlet-rendszer megoldásgörbéi egyenesek, vagyis a sík geodetikus vonalai egyenesek. A gömb geodetikus vonalai pedig a kiválasztott pontra illeszkedő főkörök.

Negyedszer: ha a felületre egy egyenes illeszkedik, akkor az természetes módon geodetikus. Ugyanis nemcsak felületi, de minden térbeli görbe között is ez a legrövidebb. Egyébként egy nem egyenes felületi görbe akkor és csak akkor geodetikus, ha a felületi normálisnak és a görbe főnormálisának iránya megegyezik. Ugyanezt másképp fogalmazva: a geodetikus simulósíkja a felület normálsíkja, vagy a rektifikáló síkja a felület érintősíkja.

Ötödször: Newton első törvénye szerint egy anyagi pont erőhatás hiányában egyenes pályán (és egyenletesen) mozog. Ha az anyagi pont mozgását olyan erő határozza meg, amelyet egy felület fejt ki kényszerként (súrlódás nélkül), akkor az anyagi pont a felület geodetikus vonalai mentén fog mozogni. A kényszererő ugyanis mindig merőleges a felületre, Newton második törvénye szerint a tömegpont gyorsulása is ilyen irányú (azaz a kinetikus energiáját nem tudja megváltoztatni, vagyis a sebessége állandó). Ha tehát a felület egy sík, akkor egyenes pályán (geodetikus mentén), egyéb felület esetén szintén geodetikus mentén mozog, hiszen a gyorsulása, azaz a pályájának a főnormálisa merőleges a felületre, vagyis párhuzamos a felület normálisával.

Geodetikus görbület

A következőkben a felületi görbék újabb, de talán a legfontosabb görbületét fogjuk definiálni. Egy

felületi görbe P₀ pontbeli geodetikus görbületén annak az x* görbe görbületét értjük, amelyet úgy kapunk, hogy a görbét merőlegesen levetítjük a felület P₀ -beli érintősíkjára. Ennek a geodetikus görbületnek a nagysága:

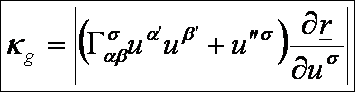
A geodetikus görbületet pozitív vagy negatív előjellel láthatjuk el attól függően, hogy a felületi normális végpontjából nézve az érintővektor pozitív, illetve negatív forgással vihető át a vetületi görbe főnormális vektorába. A geodetikus görbület a pontbeli érintővektor, annak deriváltja és a felület normálisával ís felírható (vegyes-szorzatként):

A geodetikus görbület nem más, mint a felületi görbének az őt érintő geodetikus vonalhoz viszonyított görbülete. Ebből az adódik, hogy egy felületi görbe akkor és csak akkor geodetikus vonal, ha geodetikus görbülte eltűnik. Mivel a geodetikus görbület csak a felület alapmennyiségeinek függvénye, így csak a felület belső geometriájától függ. Ennek az a következménye, hogy a geodetikus vonal a hajlítással szemben invariáns. Hajlítással kaphatunk például síkból hengert vagy kúpot. A hajlítással szembeni invariáns tulajdonságok vizsgálata a felület belső geometriáját jelenti. Ez vezet például a Riemann geometriához, amellyel ez a cikksorozat már nem foglalkozik.

Következő lap: http://gorbem.hu/MT/DiffGeom18.htm