Differenciálgeometria (12)

Példák felületi görbék hosszára és hajlásszögére

1.

Határozzuk meg a hiperbolikus paraboloid paramétervonalainak hajlásszögét. A felület paraméteres egyenletrendszere:

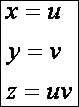
Paramétervonalak (egyenesek):

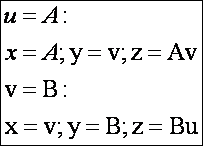
Paramétervonal-érintők:

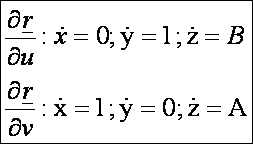
A felület első alapmennyiségei:

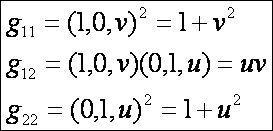
A paramétervonal-érintők szögének koszinusza:

Ha az A és B -ből valamelyiket, vagy akár mindkettőt nullának választjuk, akkor a paramétervonalak (amelyek itt egyenesek) merőlegesek egymásra. Nézzünk két pár paramétervonalat:

A = 1; B = 1; (kék, az egyik az x tengelyen) és A = -0,5; B = -0,5 (piros)

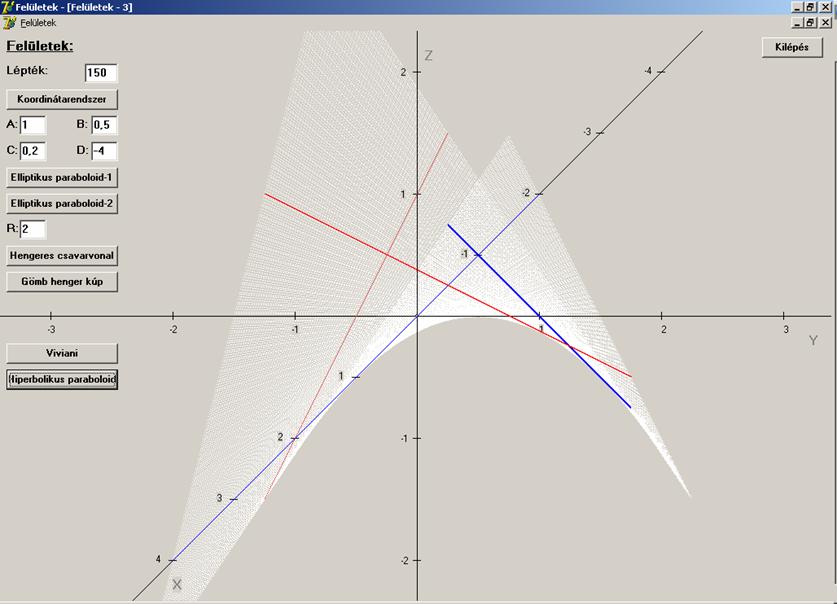
2.

A következő példánkban adott egy felület és rajta két felületi görbe. Határozzuk meg a két felületi görbe szögét. A felület:

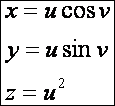
A két felületi görbe:

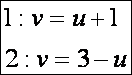
A felület első alapmennyiségei:

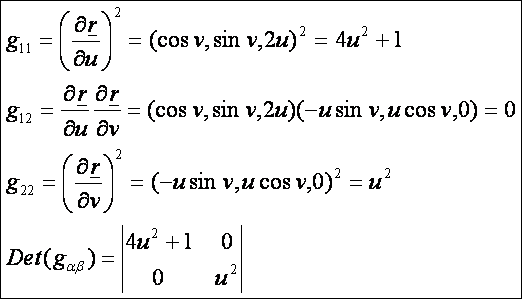
A felületi görbék paraméteres egyenletrendszerei és deriváltjai:

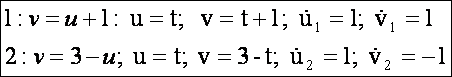
A két felületi görbe metszéspontja:

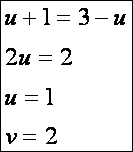
A két görbe szögének koszinusza:

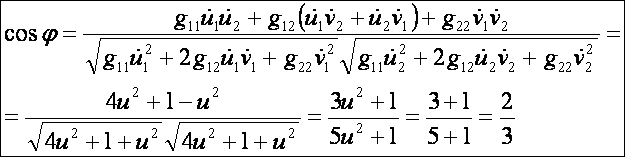
3.

Következő példánkban határozzuk meg a

első alapformával rendelkező felületnek a

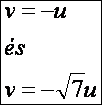
felületi görbéinek a szögét. A megadott alapforma szerint az első alapmennyiségek:

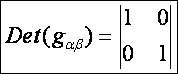
A felületi görbék paraméteres egyenletrendszerei és deriváltjai:

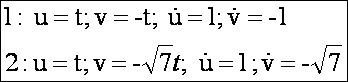
A két görbe a t = 0 -ban metszi egymást. Így a szög:

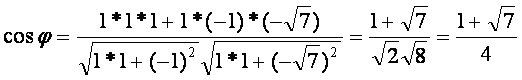
4.

Ebben a példánkban egy felület görbe-vonalú háromszögének oldalait és szögeit kellene meghatározni. Legyen a felületünk egy egyenes csavarfelület:

Először határozzuk meg a csavarfelület első alapmennyiségeit:

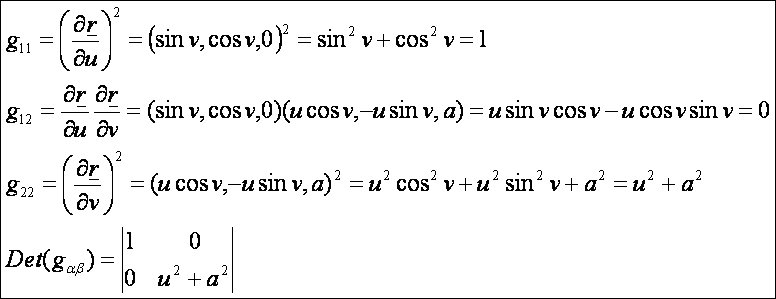
Legyen megadva a felület görbe-vonalú háromszöge a következőképpen:

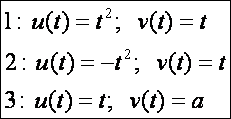
Ezek deriváltjai:

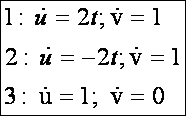
A felületi görbék szöge az első alapmennyiségekkel. Az 1 és 2 görbe szöge:

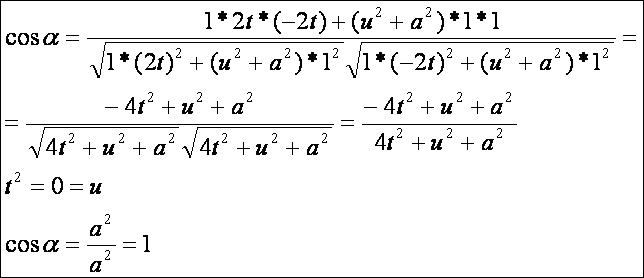
Az 1 és 3 görbe szöge:

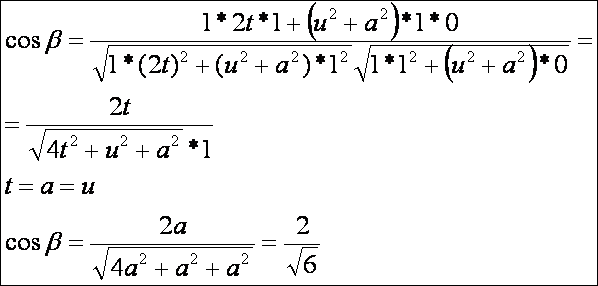
A 2 és 3 görbe szöge:

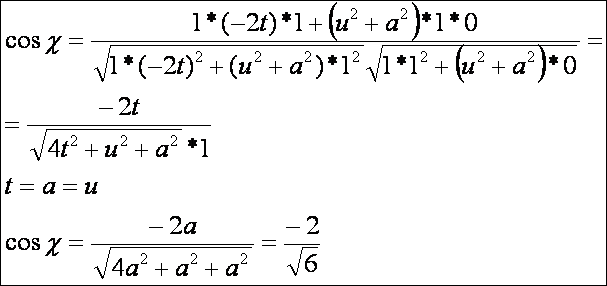
Írjuk fel a három felületi görbe egyenletét:

Azért, hogy a feladatot még jobban értelmezni tudjuk, ábrázoljuk a felületet és rajta a görbe-vonalú háromszöget:

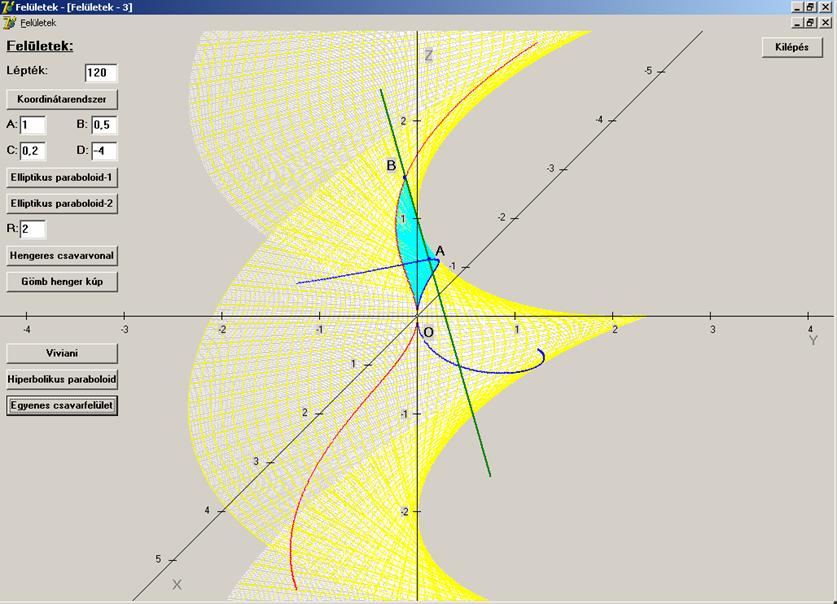
A kék és piros görbék metszéspontja az O pont:

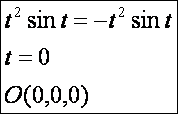
A kék és zöld görbék metszéspontja az A pont:

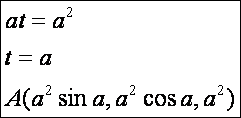
A piros és zöld görbék metszéspontja a B pont:

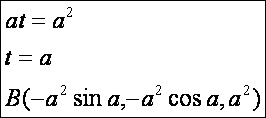
A háromszög oldalainak hossza. OA görbe:

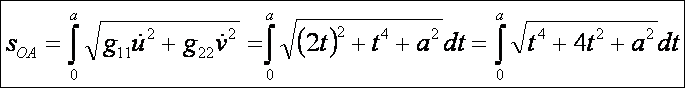
OB görbe:

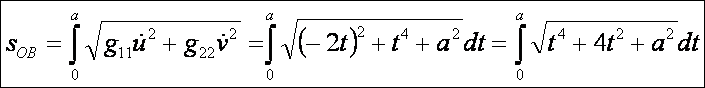
AB szakasz:

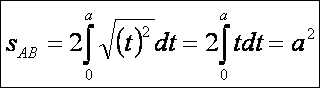
Vagy AB mint két pont távolsága:

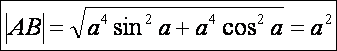
Írjuk fel a három felületi görbe érintőjét:

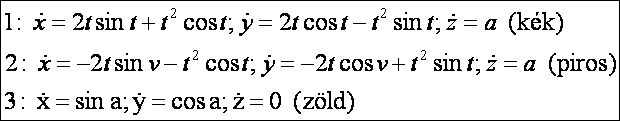
Számítsuk ki az AOB szög nagyságát. A két érintővektor:

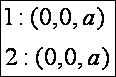
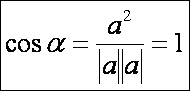
Mivel a két vektor azonos, a szög nagysága nulla, vagyis a két görbe érinti egymást.

Következik az OAB szög nagysága. A két érintővektor:

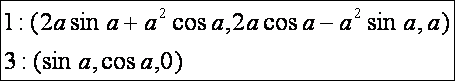
Az 1 -es vektor nagysága:

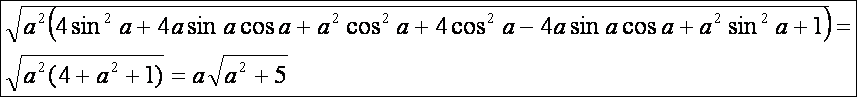
Így a szög koszinusza:

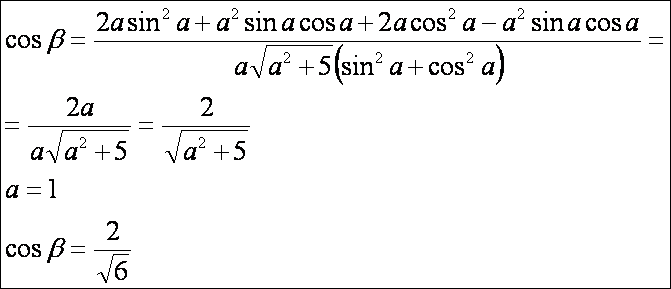
Végül az OBA szög nagysága:

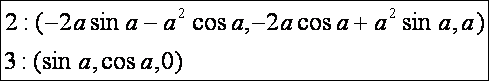
Mivel a 2 -es vektor ugyanakkora, mint az 1 -es vektor, ezért OBA szög koszinusza:

5.

Most tekintsük a Viviani-görbét a gömb felületi görbéjeként. Számítsuk ki mekkora szöget zár be a Viviani-görbe két ága a kettős pontjában. Tudjuk, hogy a felületi vektorok szögét így számíthatjuk ki:

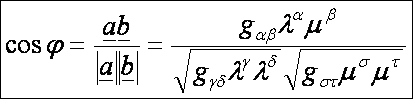
Ennek a képletnek az alkalmazásához meg kell adni a két érintővektornak a gömb paramétervonal-érintői által meghatározott koordinátáit, azaz a érékeket. A gömb és a paramétervonalak egyenlete:

Paramétervonal-érintők:

értéke az u = 0 és v = 0 helyen, amely az x = R síkban van:

A Viviani görbe a gömb egyenletéből származtatva:

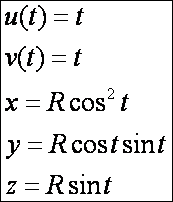
Az érintővektor:

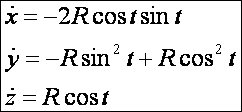
A Viviani-görbe két érintővektora a t = 0 és t = pi paramétereknél:

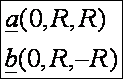
Ennek a két vektornak a koordinátái a paramétervonal-érintők rendszerében:

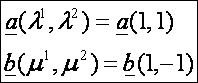
A gömb első alapmennyiségei:

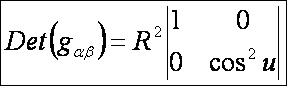
Ezek alapján a Viviani-görbe kettős pontjában az ívek szöge:

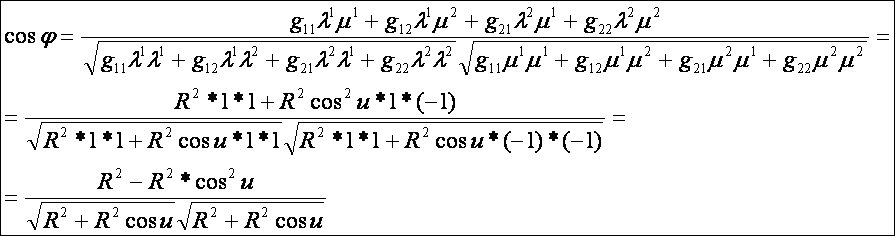
Mivel a görbe kérdéses pontjában u = 0, így:

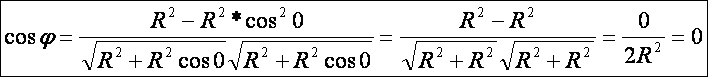
Azaz a Viviani-görbe két ága a kettős pontjában 90 fokos szöget zár be.

Most tekintsük a Viviani-görbét egyszerűen csak térgörbének és így határozzuk meg két érintőjének a szögét. Tehát a görbe:

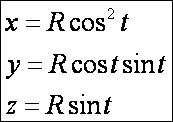
Az érintővektor a t pontban:

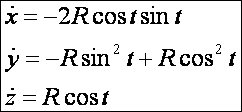
Az érintővektor t = 0 és t = pi pontban:

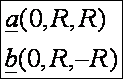
Azaz a kettős pontban a görbe önmagát valóban merőlegesen metszi. Mindezt egy rajzon is megtekinthetjük (a gömb és a paramétervonalak színe piros, az érintősík fehér, a paramétervonal-érintők zöldek, a görbe két érintővektora fekete):

Következő lap: http://gorbem.hu/MT/DiffGeom13.htm