Differenciálgeometria (10)

További példák felületekre

Mielőtt a felületek differenciálgeometriájába kezdenénk, még megrajzolnánk néhány ismert vagy kevésbé ismert felületet. Közös lesz bennük a speciális származtatás. Lesznek köztük forgásfelületek, különböző vonalfelületek és csavarfelületek is. Az ábrázoláskor a paramétervonalakat mindig feltüntetjük.

Forgásfelületek

Keletkezzen egy forgásfelület egy g(u) görbe z tengely körüli megforgatásából. Ekkor a forgásfelület egyenlete:

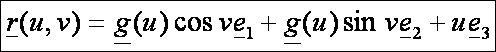
Ez alapján ábrázoljuk a következő görbe által előálló forgásfelületet:

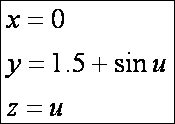
A forgásfelület egyenletrendszere:

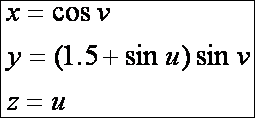
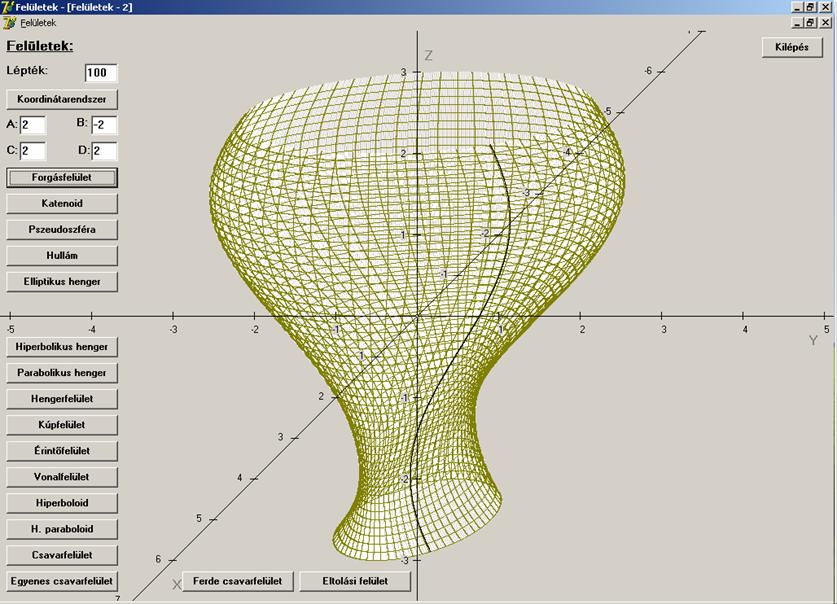
Az u szerinti paramétervonalak a megadott görbének a z tengely körüli elforgatottjai (a u = 0.66 értékre feketével megrajzolva), a v szerinti paramétervonalak pedig körök.

Ha a homogénnek tekintett gravitációs térben egy tökéletesen rugalmas, egyenletes tömegeloszlású kötelet úgy fűgesztünk fel két pontban, hogy a két pont távolsága kisebb, mint a kötél hossza, akkor a nyugalomban lévő belógó kötél alakja a koszinusz hiperbolikusz függvény alakjával megegyezik. Szokás ezért ezt a görbét láncgörbének is nevezni. Ilyen alakot vesz fel minden légkábel, vagy egy terheletlen szárítókötél is. 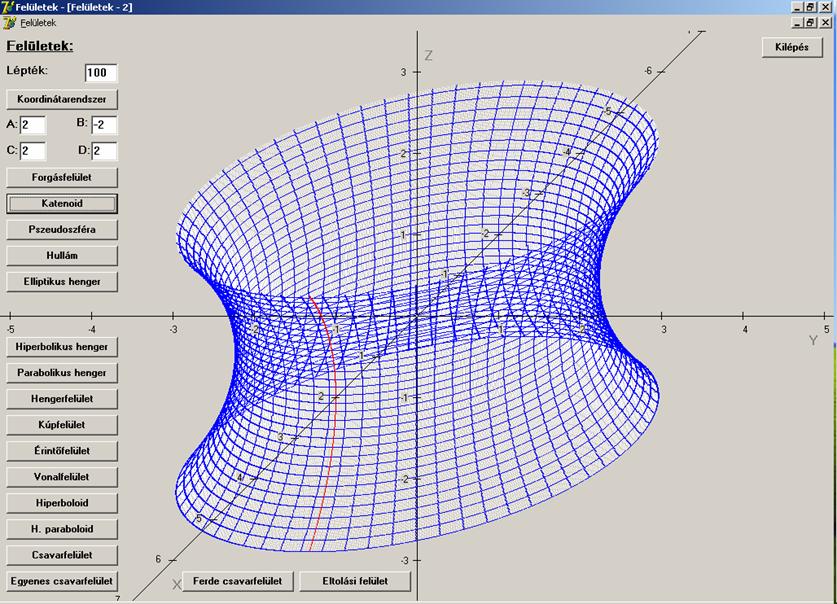Ennek a görbének tengelyére merőleges egyenes körüli megforgatásával katenoidnak nevezett felület keletkezik, ha a forgástengelynek és a függvénynek nincs közös pontja. Ez a felület egy úgynevezett minimál-felület. Ezt a felületet (gravitációt most nem vesszük figyelembe) két párhuzamos síkú kör alakú drótnak szappanos vízbe való merítésével, majd kiemelésével létre lehet hozni (ha elég ügyesek vagyunk). A drótkeretek között kifeszülő szappanhártya pontosan katenoid alakot vesz fel. A felületi feszültség hatására ugyanis minimális felület alakul ki. Már maga a láncgörbe is a minimális helyzeti energiájú alakot veszi fel a gravitációs térben. Tekintsük a következő láncgörbét:

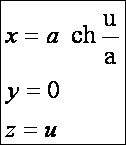
Ennek a z tengely körüli megforgatásából keletkező katenoid egyenlete:

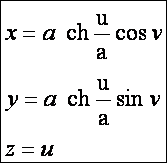
Ennek a rajzát láthatjuk a következő ábrán, ahol pirossal egy láncgörbét is megrajzoltunk. A felület v szerinti paramétervonalai körök, az u szerintiek láncgörbék.

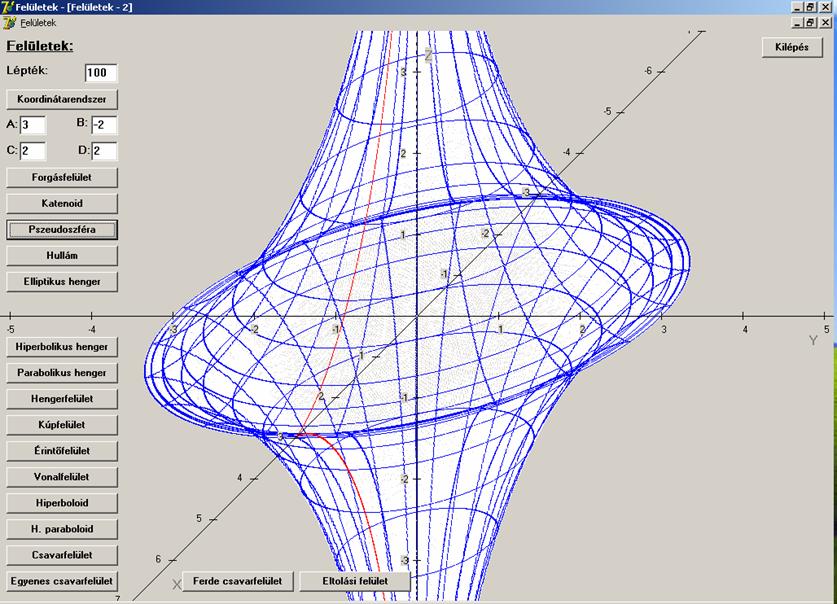
Ha a traktrix nevű síkgörbét az asszimptotája körül megforgatjuk, akkor pszeudoszférát kapunk. Ennek a felületnek az úgynevezett Gauss-féle görbülete állandó (úgy, mint a gömbbé), de ennek negatív. A pszeudoszféra egy véges darabján a hiperbolikus geometria (végtelen sok párhuzamos) érvényes. Tekintsük a következő tratrixot:

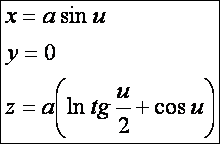
Ennek a z tengely az asszimptotája. Forgassuk meg a z tengely körül. Írjuk fel a felület egyenletrendszerét:

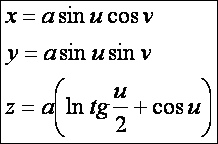
A rajzon pirossal egy v = 0 paraméterhez tartozó tratrixot is megrajzoltunk. Az u szerinti paramétervonalak körök.

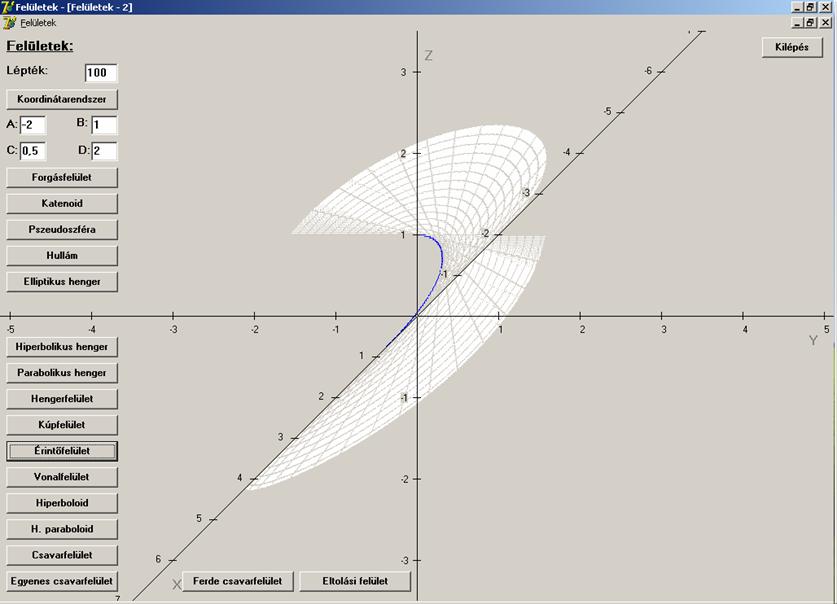
A = 3

Ha a nyugodt vízfelületre egy pontszerű tárgy becsapódik, akkor a becsapódási ponttól felületi hullámok indulnak ki. Ha elég közel vagyunk a becsapódási ponthoz, akkor szinusz-hullámokat látunk. E képződményt jól közelíti egy szinuszgörbe z tengely körüli megforgatásával kapott felület. Legyen a görbénk:

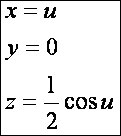
A hullámfelület egyenletrendszere:

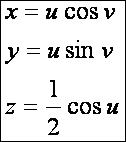
A felület u szerinti paramétervonalai szinuszgörbék, a v szerintiek körök. A v = 0 -hoz tartozó szinuszgörbét pirossal megrajzoltuk.

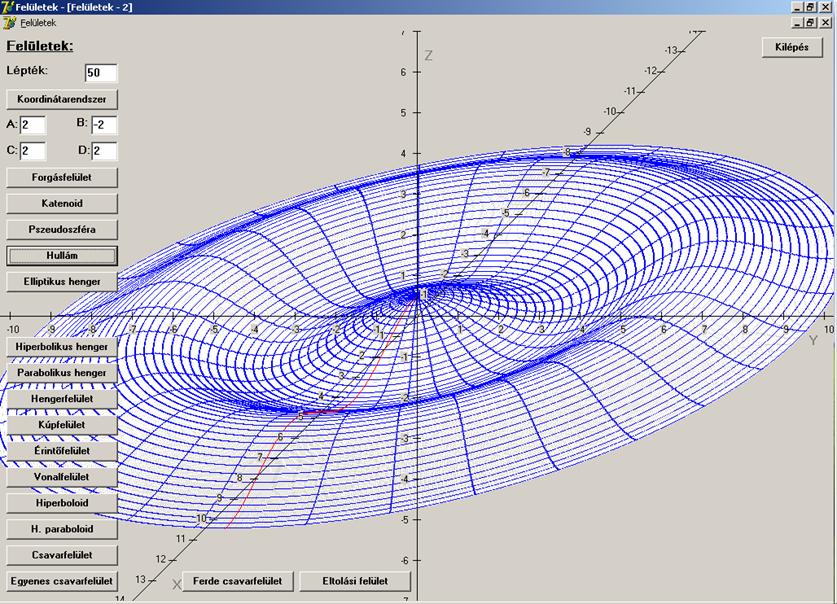
Mindenki, aki eddig eljutott jutalmat érdemel. Volt valaha egy TV műsor, amelyben ezt osztogattak. Íme a hullám újragondolva:

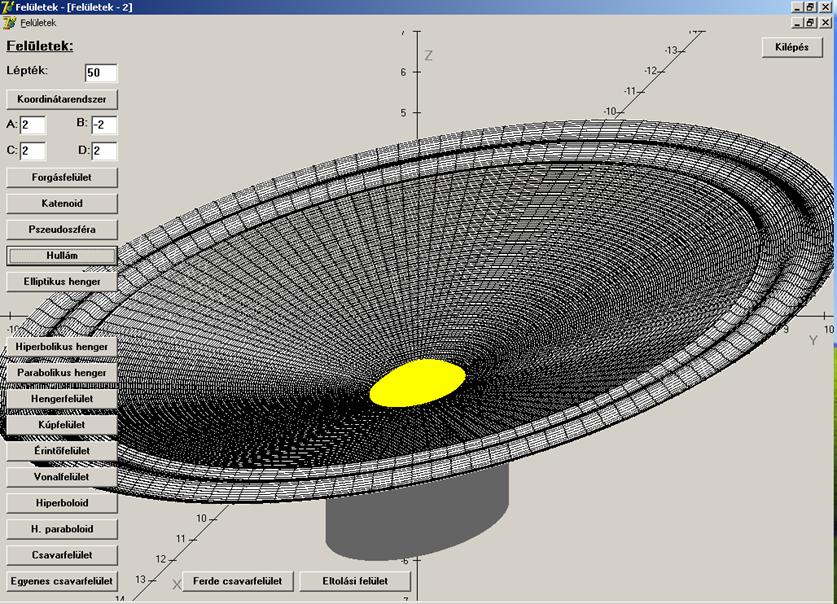
Vonalfelületek

Az olyan felületet, amelynek minden pontjára olyan egyenes illeszthető, melynek a pontot tartalmazó szakasza a felületre illeszkedik, vonalfelületnek, az egyenest a vonalfelület alkotójának nevezzük.

Ha a vonalfelület érintősíkja minden alkotója mentén végig ugyanaz, akkor a vonalfelületet torzfelületnek nevezzük.

Minden torzfelülethez létezik egy olyan térgörbe, amelynek érintőfelülete a kérdéses torzfelület. Ezt a görbét a torzfelület oromvonalának (vagy oromnak) is szokták nevezni. Hengerfelület esetén az orom a végtelen távoli pont, kúpnál az orom a kúp csúcspontja. Megjegyezzük, hogy minden érintőfelület egyben torzfelület is.

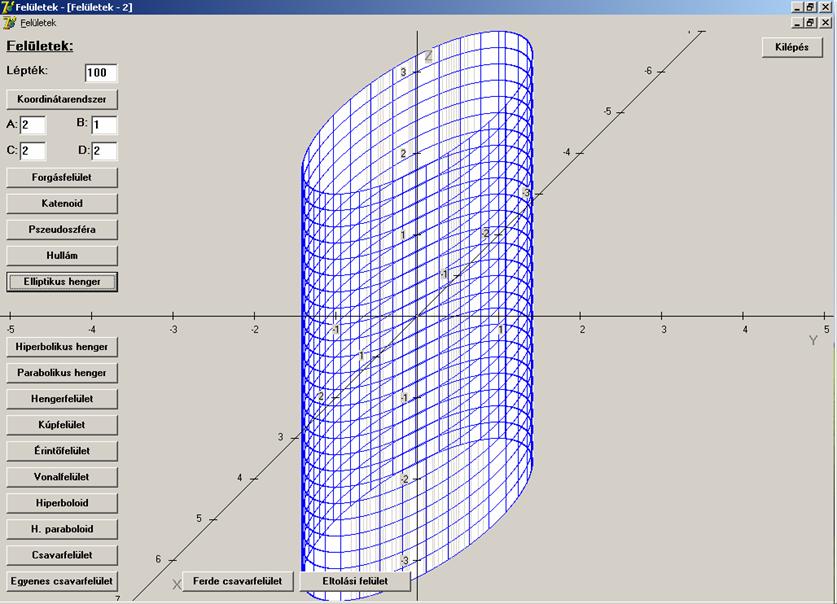
Kezdjük a rajzolgatást a torzfelületekkel. Elsőnek nézzük az elliptikus hengert. A henger tengelye a z koordinátatengely. A v szerinti paramétervonalak ellipszisek, az u szerintiek pedig egyenesek:

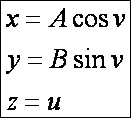
A = 2; B = 1

Második felületünk a hiperbolikus henger lesz. Szimmetrikus az origóra és a koordinátasíkokra. Az u szerinti paramétervonalak hiperbolák, az v szerintiek egyenesek:

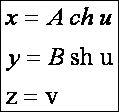
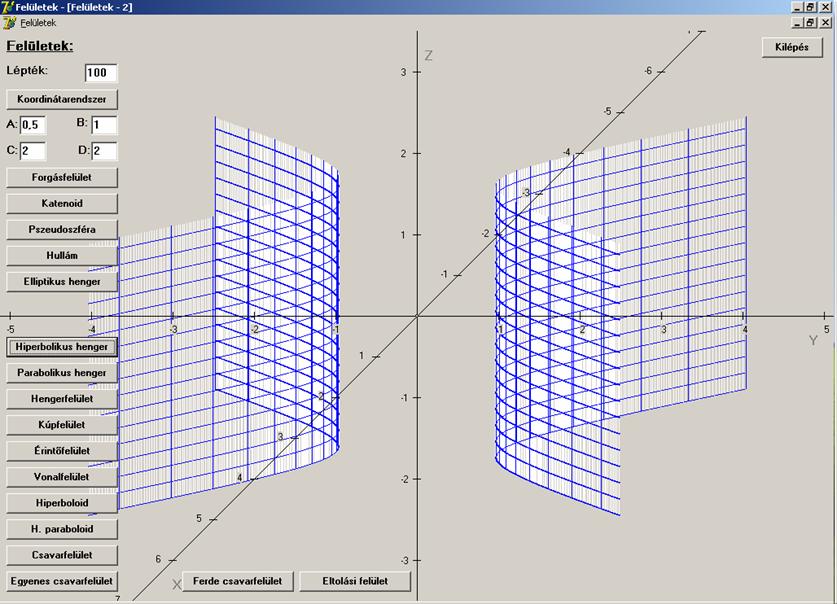
A = 0,5; B = 1

A következő hengertípus a parabolikus henger. A z tengely az egyik alkotója, szimmetrikus az (x, y) és az (y, z) síkra. Az u szerinti paramétervonalak parabolák, az v szerintiek egyenesek:

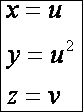
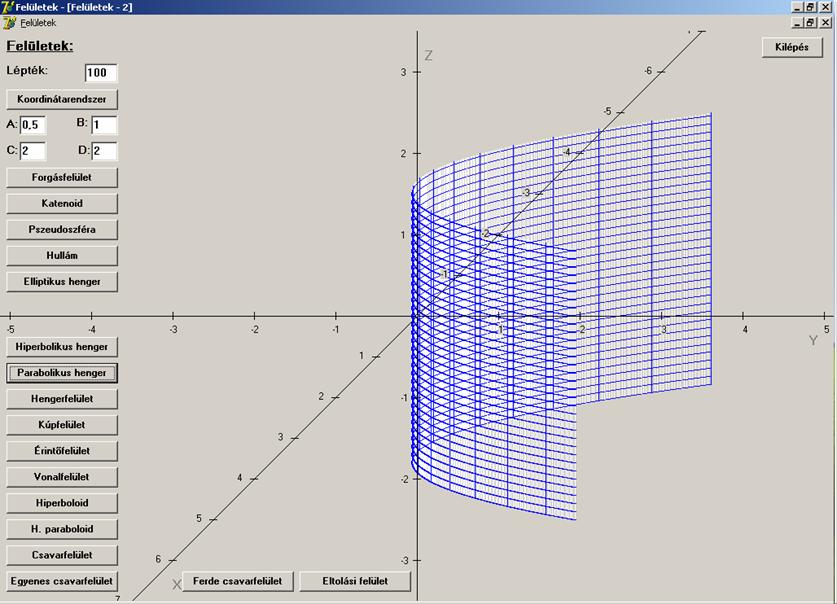
Most nézzünk még általánosabb hengerfelületet. Ha megadunk egy g(u) görbét és egy a vektort, akkor a görbe minden pontját eltolhatjuk a vektor egy skalárszorosával, mely révén a henger palástjának pontjait kapjuk. Az általános egyenlet:

A g(u) itt egy tehát olyan térgörbe, mely a felület minden alkotóját pontosan egyszer metszi, az a vektor pedig a megfelelő alkotó irányába mutat. Lássunk egy konkrét példát. Legyen a görbe:

Ezt a görbét a rajzon piros színnel tüntettük fel. A vektor pedig:

A konkrét általános hengerfelület paraméteres egyenletrendszere:

Az u szerinti paramétervonalak a megadott görbével „párhuzamosak”, az adott vektor (a rajzon fekete színnel) irányú vektorral vannak eltolva, a v szerinti paramétervonalak egyenesek.

A = -2; B = 1; C = 0,5

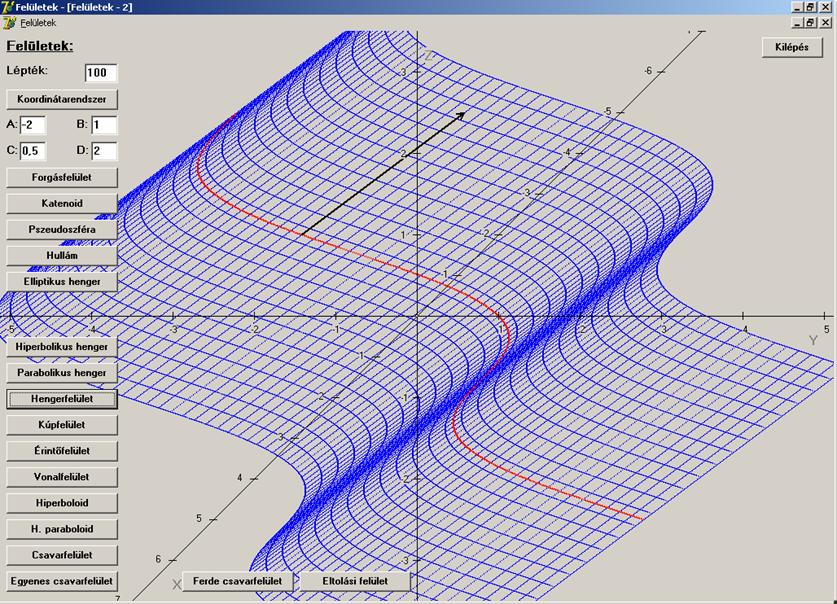
A torzfelületek másik csoportja a kúpfelület. Következzen tehát az általános kúpfelület. Az g(u) vezérgörbéjű és K(A, B, C) csúcspontú kúpfelület egyenlete:

Az ábrázoláshoz vegyünk konkrét görbét és csúcspontot:

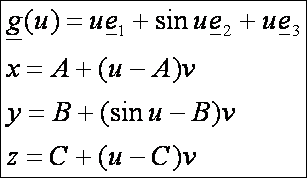
A v szerinti paramétervonalak egyenesek, melyek a K csúcspontra illeszkednek. Az u szerinti paramétervonalak egymáshoz hasonlóak, a hasonlósági középpont a kúp K csúcspontja.

A = -2; B = 1; C = 0,5

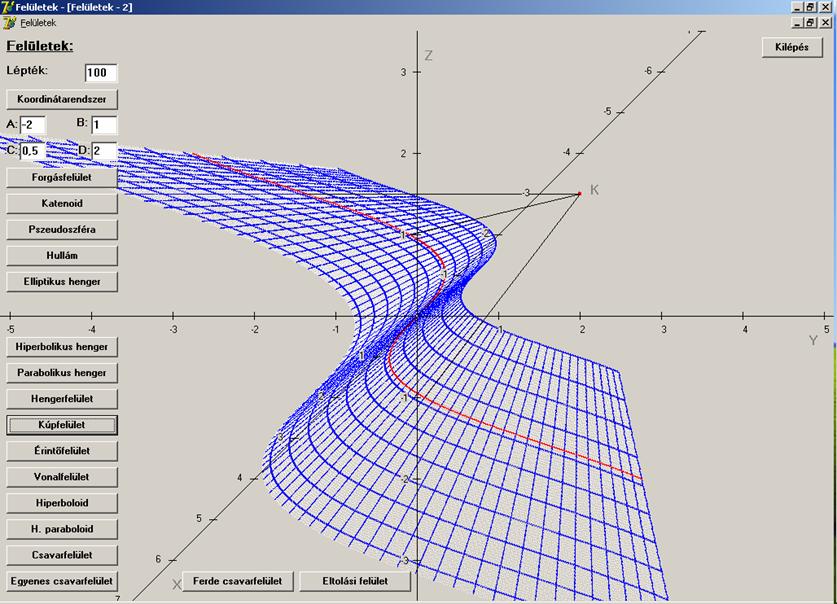
Az eddig lerajzolt vonalfelületeknek vagy a végtelenben (henger) vagy a végesben (kúp) van egy olyan pontja, amelyiken minden alkotó vagy annak meghosszabbítása átmegy. Most nézzünk példát egy érintőfelületre, amely mint azt fentebb említettük, torzfelület is. Ennek az alapgörbéje a g(u) egyúttal a felület oromvonala is. Először lássuk az általános egyenletet:

Legyen a görbe és érintője:

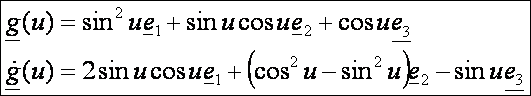
Ez egyébként a Viviani-féle görbe. Nézzük az érintőfelületünk egyenletrendszerét:

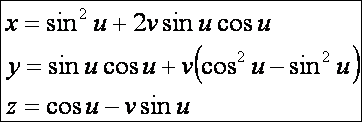
A rajzon a Viviani-görbe negyed része kék színnel van jelölve. A v szerinti paramétervonalak egyenesek. Paramétertartományok pedig u: 0 – Pi/2 és v: -Pi/2 – Pi/2.

Megemlítenék még egy tulajdonságot a vonalfelületekkel kapcsolatban. Ez pedig a lefejthetőség, amely alatt a felületnek a síkra való izometrikus leképezhetőségét értjük. Minden torzfelület lefejthető felület, és minden lefejthető felület vagy henger-, vagy kúp- vagy érintőfelület. A lefejthetőség két felület között is értelmezhető, ekkor hajlításnak nevezzük (természetesen a lefejthetőség tulajdonságaival). A lefejthetőséget a következőképpen szemléltethetjük: egy felület lefejthető, ha a felületet nem nyújtható anyagból elkészítjük, akkor síkba egyszerűen kiteríthető (ha szükséges, akkor valamely paramétervonala mentén előbb felvágjuk – például henger esetén).

Most nézzünk példákat olyan vonalfelületekre, amelyek nem torzfelületek. A g(u) vezérgörbéjű, h(u) irányhatározójú vonalfelület vektoregyenlete:

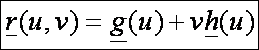
Nézzünk erre is konkrét példát:

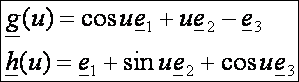
A megrajzolt felületrész paramétertartományai: u: 0,1 – 1,4 és v: 1 – 7. A v = 3,1 -hez tartozó paramétervonal piros színnel van megrajzolva. Az u szerinti paramétervonalak egyenesek (ettől vonalfelület a felületünk).

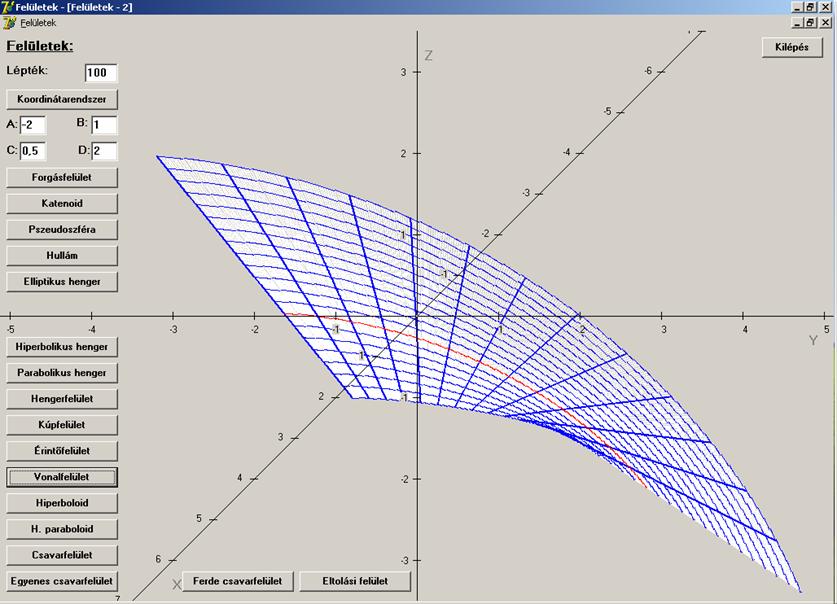
Az egyköpenyű hiperboloid és a hiperboikus paraboloid olyan vonalfelületek, amelynek nem torzfelületek és minden pontjukon nem egy, hanem két, a felülethez tartozó egyenes halad át. Ez két egyenes-sereget jelent, mely egyenes-seregek elemei egymáshoz képest kitérők. A következő két rajz ennek a tulajdonságnak a felhasználásával készült. Az egyköpenyű hiperboloid esetén felvettünk két azonosan parametrizált kört. Az egyik kör minden pontját a másik kör két olyan pontjával kötöttük össze egyenes szakasszal, melyek paraméterei az első pont paramétereitől mindig azonos mértében térnek el pozitív és negatív irányban. Ezzel a paraboloid alkotóit rajzoltuk meg, kialakítva a felület látványát.

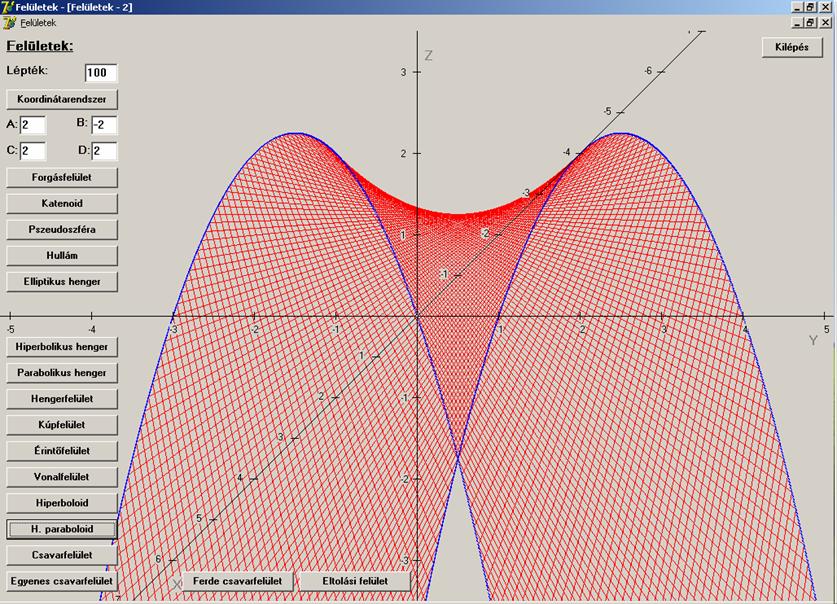
A hiperboikus paraboloidnál hasonlóan jártunk el, csak itt a két vezérgörbe két egybevágó parabola volt. Ezt kaptuk:

Csavarfelületek

Ha egy görbét úgy mozgatunk a térben, hogy minden pontja azonos tengelyű és menetmagasságú csavarvonalat ír le (ez a csavarmozgás = halad és forog), akkor görbe pontjai csavarfelületet alkotnak. Ha a görbék egy csavarvonal érintői, akkor speciális csavarfelületet kapunk, amely a síkra lefejthető.

Legyen z a forgástengely, f(u) a csavarfelület profilgörbéje, az A pedig a haladó mozgás sebességének és a szögsebességnek az aránya. Ekkor a csavarfelület egyenlete:

Példánkban legyen a profilgörbe:

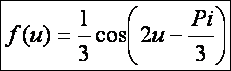
A = 0,5

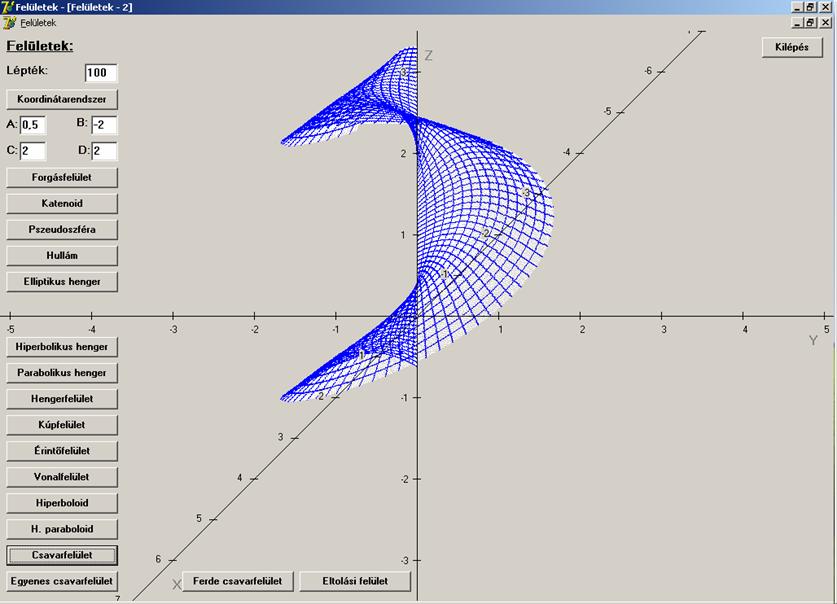
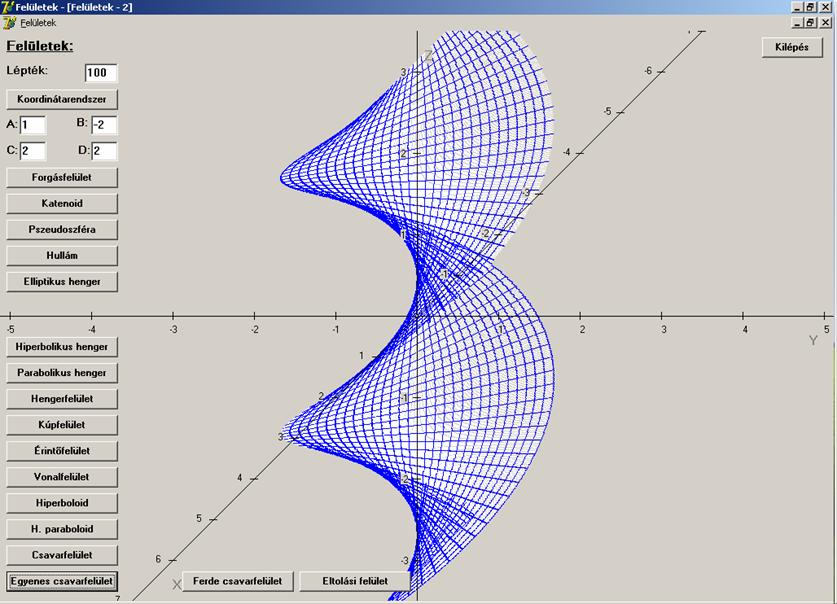
Egyenes csavarvonal esetén vonalfelületet kapunk, a v szerinti paramétervonalak a tengelyre merőleges egyenesek:

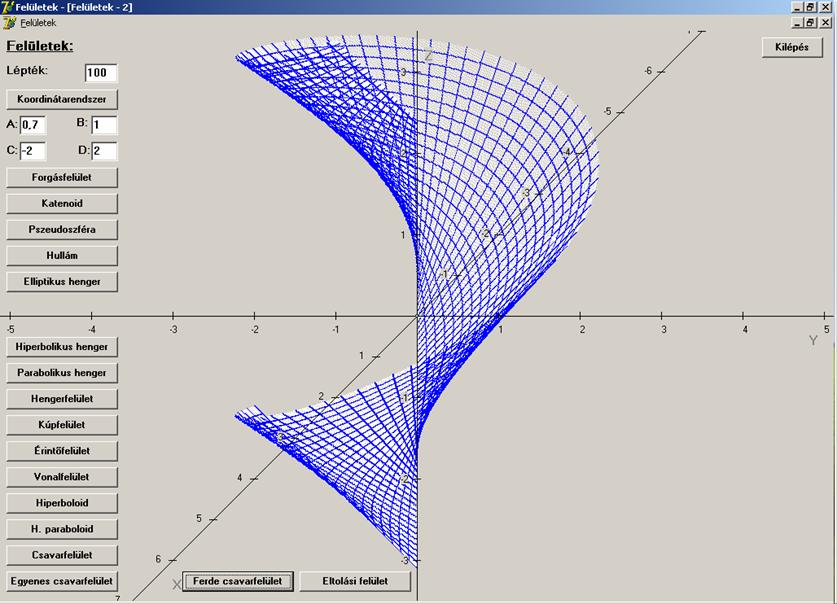
Ferde csavarvonal esetén szintén vonalfelületet kapunk. Itt a v szerinti paramétervonalak a tengellyel mindig ugyanolyan szöget bezáró egyenesek:

A = 0,7; B = 1; C = -2

Eltolási felületek

Befejezésül egy eltolási felületet rajzolnánk. Ha egy f(u) görbét úgy toljuk el, hogy a görbe minden pontja egy g(v) görbe szerint mozog, akkor eltolási felületet kapunk. Az eltolási felület egyenlete:

Példánkban f legyen a Viviani-görbe első negyede, g pedig egy szinuszgörbe:

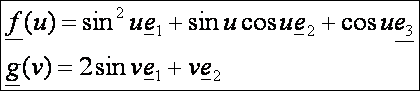
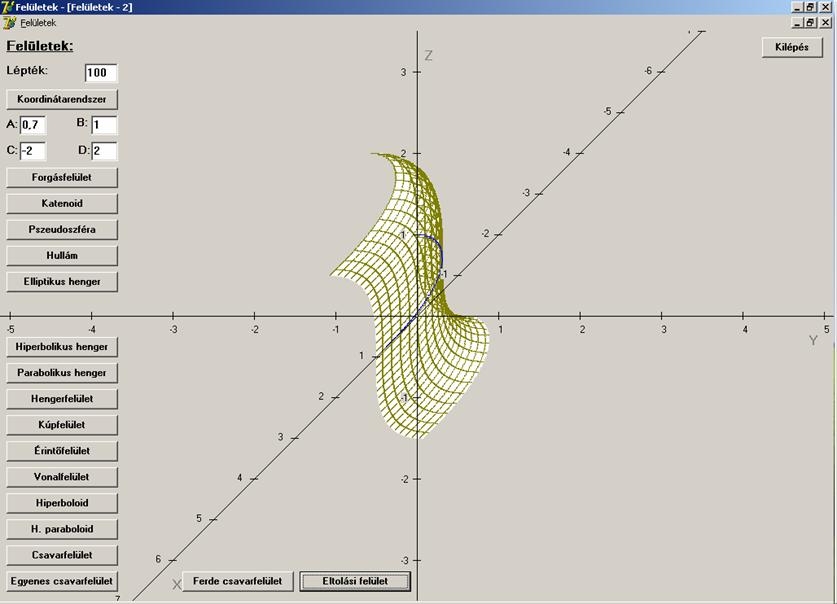
Íme az eredmény (a Viviani-görbe kék színnel jelölve):

Következő lap: http://gorbem.hu/MT/DiffGeom11.htm