Abszolút érték (2)

Implicit alakú abszolút-értékes függvények.

Ebben a részben implicit abszolút-értékes függvények ábrázolásával foglalkozom. Tehát olyanokkal, amelyek képletében (egyenletében) a függő változó nincs kifejezve a független változó és konstansok segítségével. Sőt inkább úgy fogalmaznék, hogy kifejezése még nehézségekbe is ütközik. Ettől még a függvények ábrázolása könnyen megoldható. Az ábrázolást követően legtöbbször azzal szembesülünk, hogy a keletkezett relációk nem függvények. Egy független értékhez több érték is (gyakran kettő, néha három vagy végtelen sok) tartozik. Nem gondolnám, hogy itt emiatt visszavonulót kellene fújni. A körnek, ellipszisnek, hiperbolának is ilyen egyenleteit ismerjük és ábrázoljuk őket koordináta rendszerben. Itt is így járunk el. Kicsit a másodfokú görbékre gondolva, olyan képletekkel próbálkozom, amikor az egyik oldalon lesz egy konstans, az egyenlet másik oldalán pedig keverve a függő és független változók vagy abszolútérték-jelen belül, vagy kívül. Lássunk néhány tetszetős példát.

A körre gondolva, nézzük mit kapunk, ha a következőt ábrázoljuk:

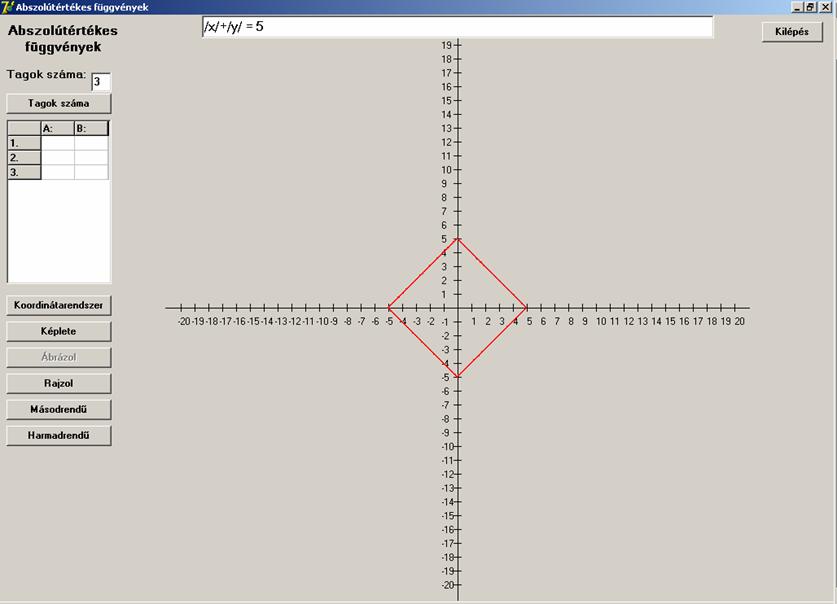
Egy négyzetet kaptunk, mely köré egy r=5 sugarú kört lehetne rajzolni. Koordináta-transzformáció segítségével toljuk el ezt a négyzetet egy v(2, 3) vektorral. Természetesen az egyenlet:

Ahogy azt a körnél megtanultuk.

Növeljük az x-et tartalmazó tagok számát:

Egy hatszöget kaptunk.

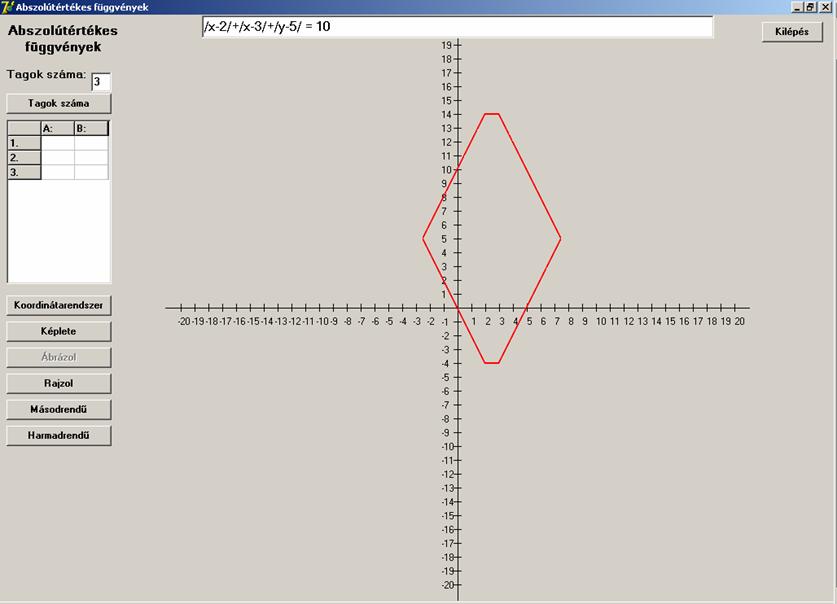
Most az y tagok száma is legyen kettő.

Ekkor egy szabályoshoz közeli nyolcszöget kapunk:

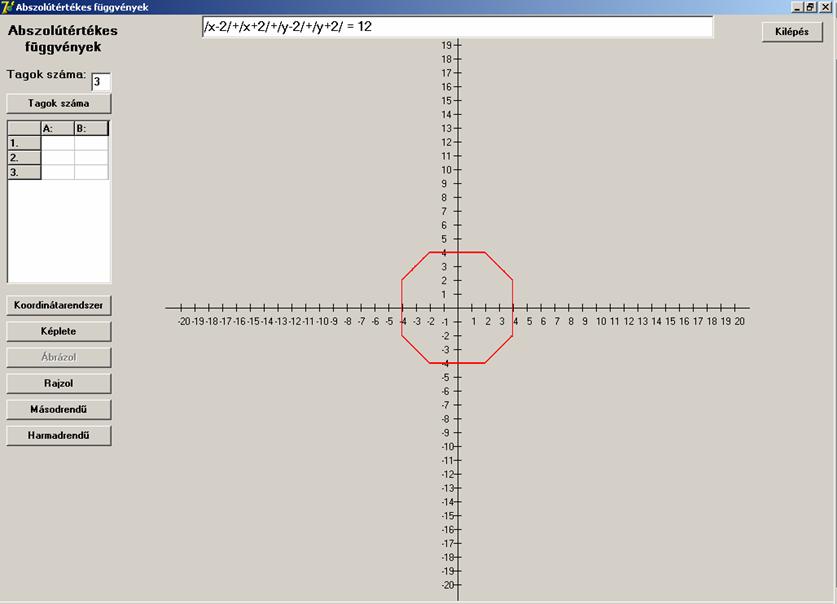
Öt tag esetén:

már egy tízszög lesz a grafikonja:

Ne csak összeadás legyen a tagok között. Először az x-et tartalmazó tag legyen negatív.

Mintha az y koordinátatengellyel párhuzamos tengelyű hiperbola lenne az eredmény (kettős V betű):

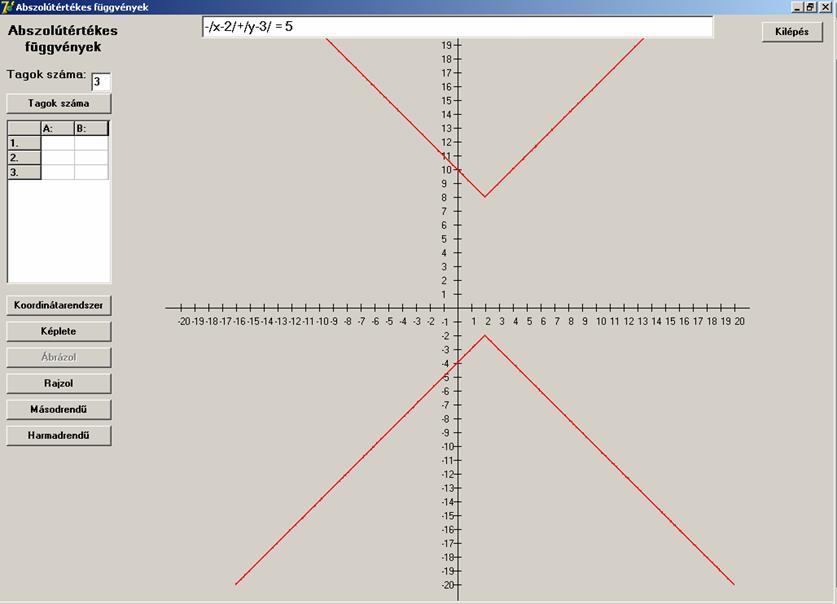
Most az y-t tartalmazó tag legyen negatív.

Ez is hiperbolához hasonló, olyan mintha x koordinátatengellyel párhuzamos tengelyű lenne (hasonlít a nagyobb – kisebb jelre):

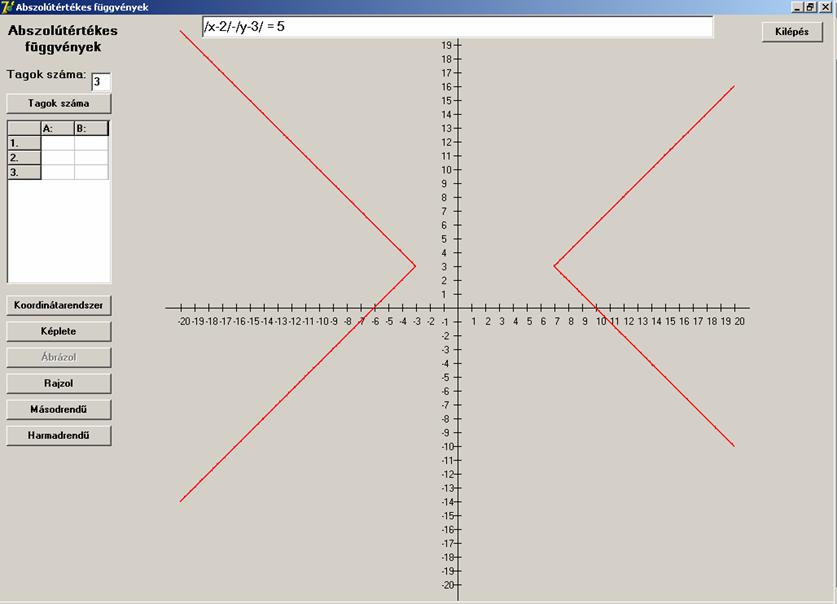
Nézzük a következő képletet.

Ez talán még jobban emlékeztet a hiperbolára:

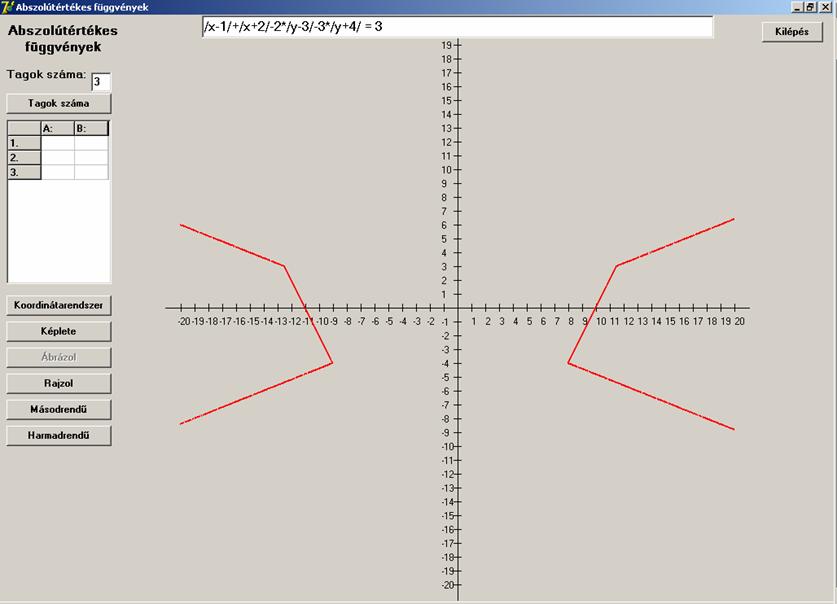
Ha tagoknak az együtthatói nem 1 abszolút-értékűek:

Ez viszont már elég vicces alakú lett:

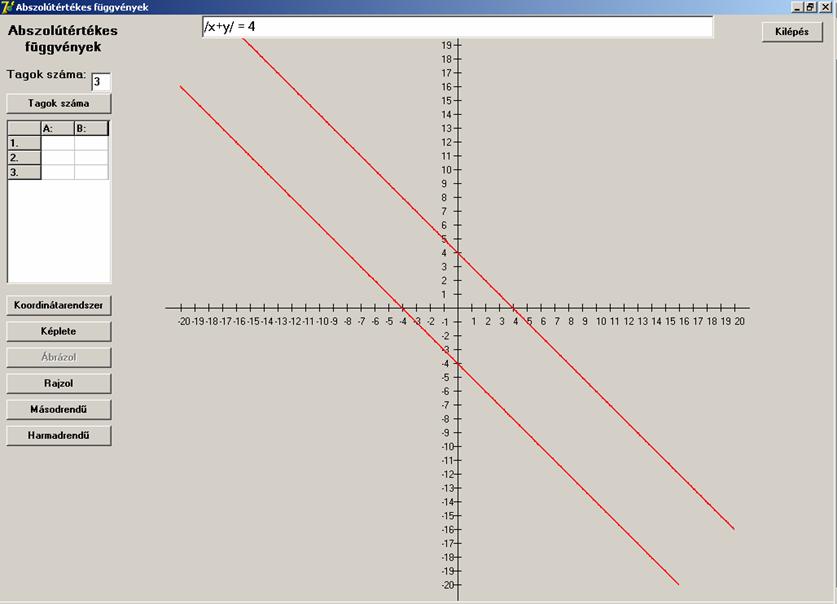
Eddig külön-külön voltak a változók. Most tegyük őket egy abszolútérték-jelbe.

Az eredmény párhuzamos egyenes-pár.

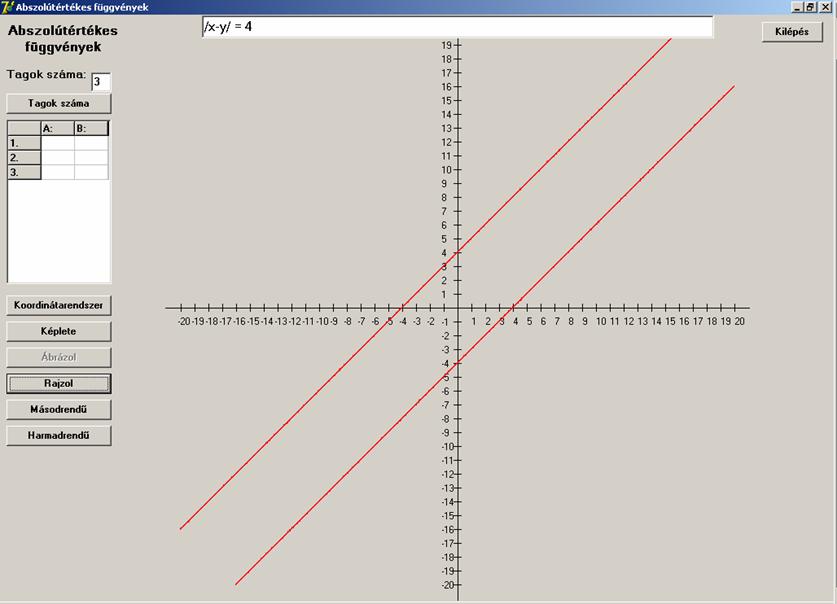
Azt gondolhatnánk, hogy a különbség egészen más, de nem.

Párhuzamos egyenes-pár pozitív meredekséggel.

Növeljünk együtthatót:

A megnövelt meredekség miatt a két párhuzamos közelebb került egymáshoz.

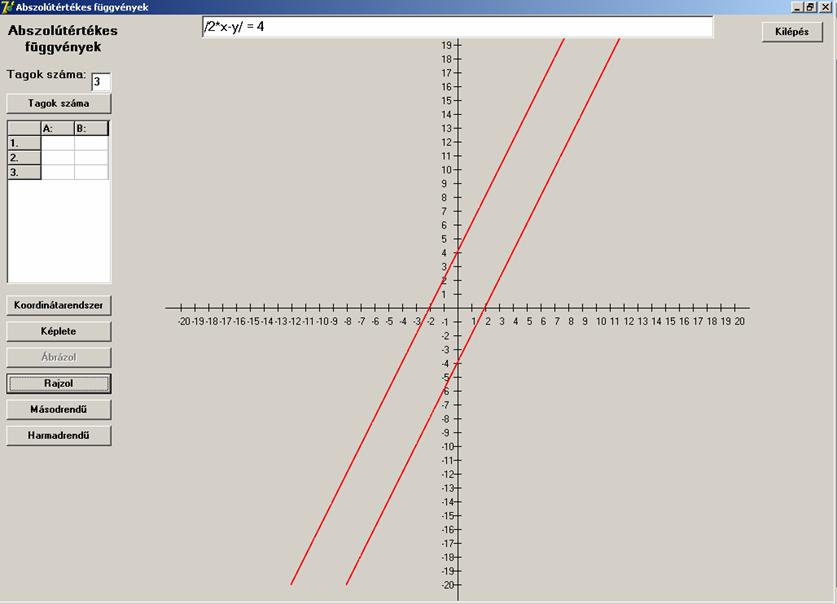
Most másodrendű alakot nézzünk:

A párhuzamosok törést szenvednek.

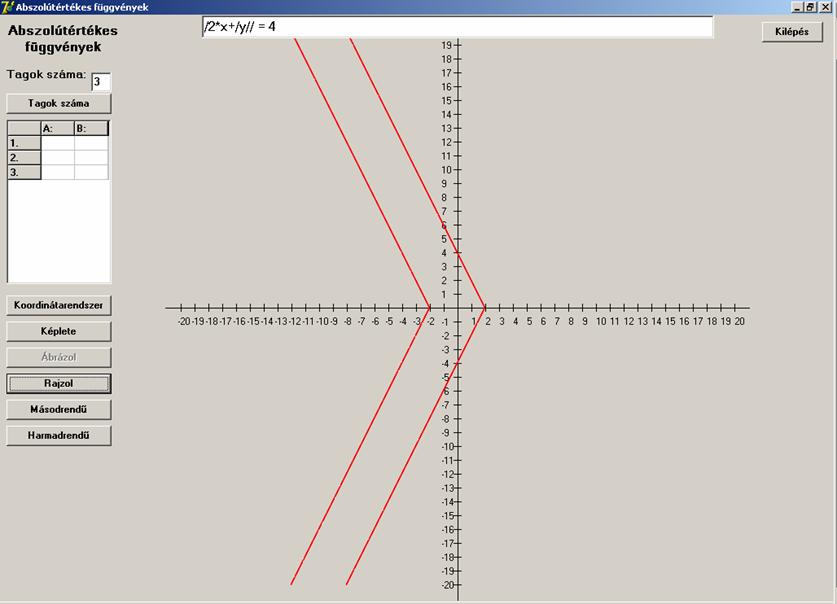
Ha a függetlennek tekintett változó kerül a második abszolútérték-jelbe, azaz

,

akkor a következőt látjuk:

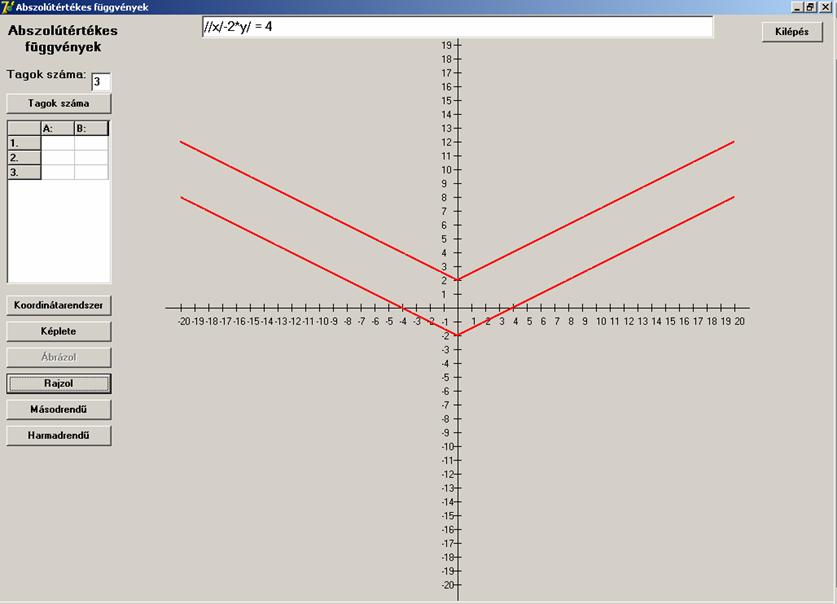
Eddig minden változó abszolútérték-jelbe volt zárva. Most legyenek szabadon is.

Az x=5 értékhez végtelen sok y érték tartozik.

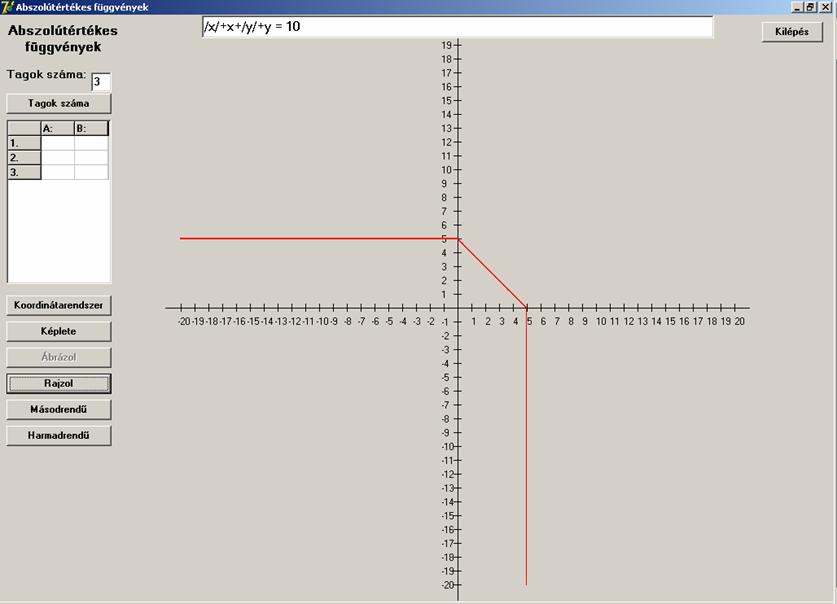
Két együtthatót változtatva a kép nagyot változik.

Íme az eredmény:

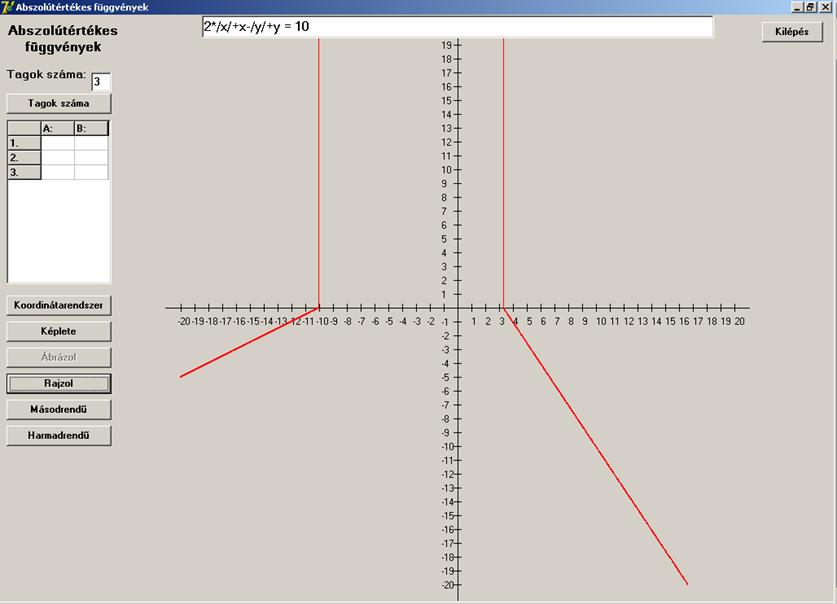
Változtassunk újabb együtthatót:

Hoppá, ez egy függvény:

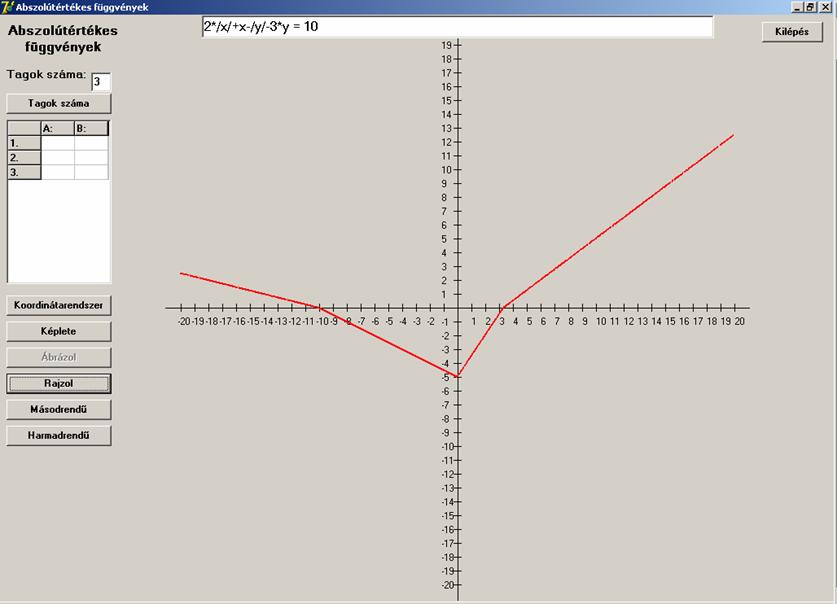
Több tagban is szerepeljenek együtt a változók abszolútérték-jelben.

Ez egy kicsit az y=1/x függvényre hajaz.

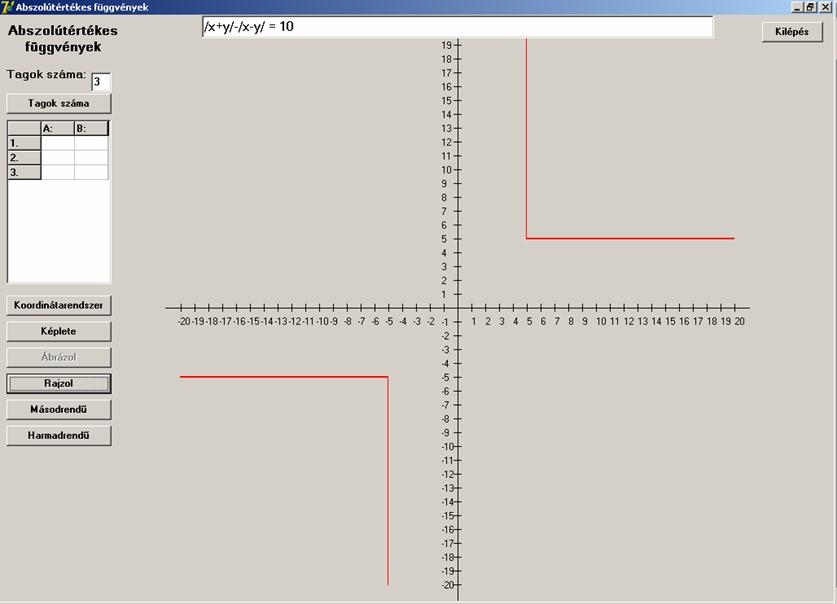
Mi lesz, ha a két tagot összeadjuk?

Egy négyzetet kaptunk.

Ha együtthatót növelünk:

Ekkor szétszakad a négyzet.

Pozitív előjelre viszont

rombusszá alakul.

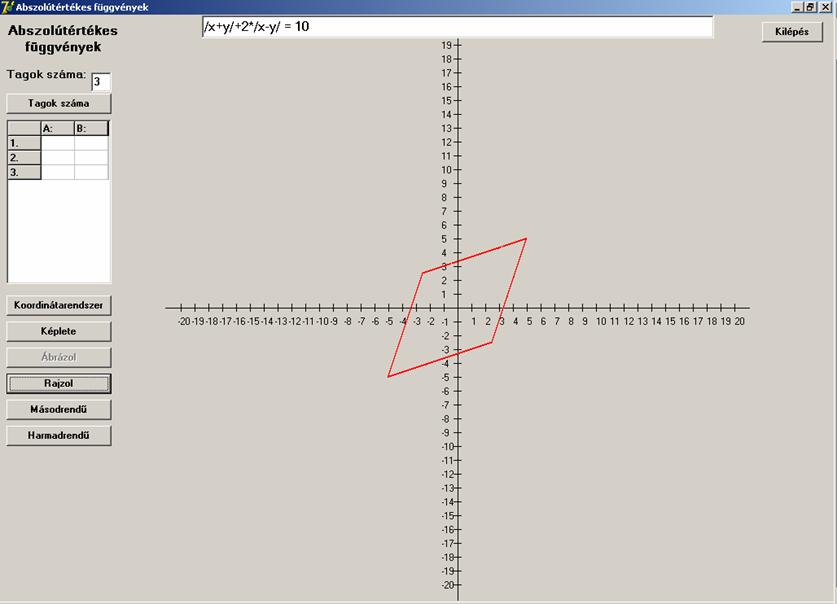
Növeljünk együtthatót az abszolútérték-jeleken belül:

Téglalapot kaptunk.

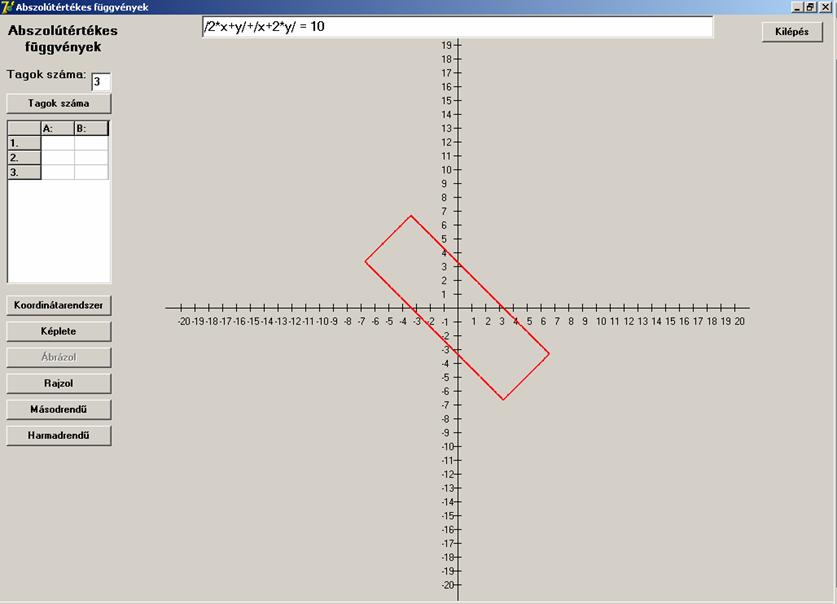
Egy előjelváltás az abszolút-értéken belül:

És egy elforgatott négyzet az eredmény.

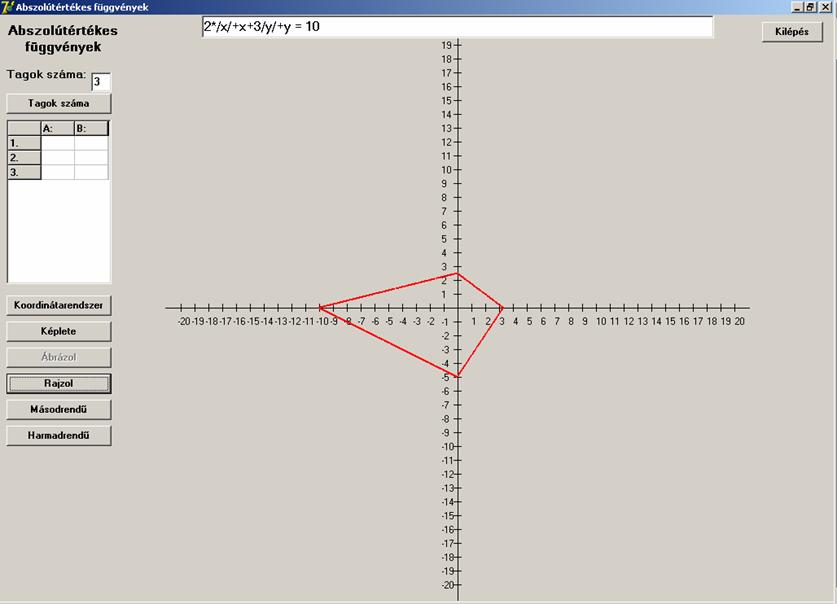
A következő képlet

Pedig egy négyszöget ad, melynek átlói merőlegesek egymásra (egyébként általános négyszög).

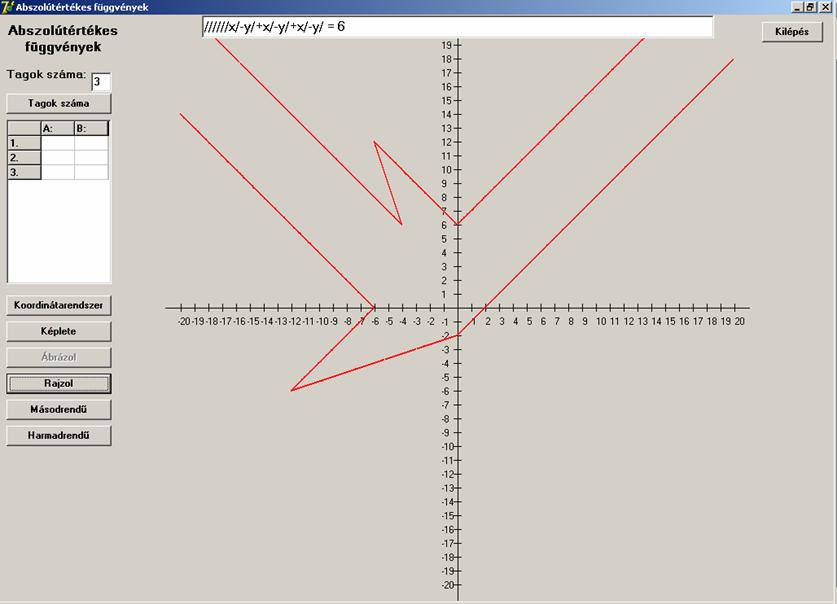
Ne fukarkodjunk az egymásba ágyazással. Befejezésül nézzük a következő hatod-rendű függvényt.

Mindenkinek a fantáziájára bízom, hogy mit lát.

Összegzésképpen mit mondhatnék? Nem könnyű rendszer találni a képletek és grafikonjaik között. Nem is biztos, hogy jó példák jutottak eszembe ebben a pár órában. Nagyon változatos grafikonok jöttek létre, szinte kizárólag olyanok, amelyek nem függvényeket határoznak meg. Még próbálkozok néhány esettel, ha valami érdekességre még rábukkanok, akkor itt közlöm majd.

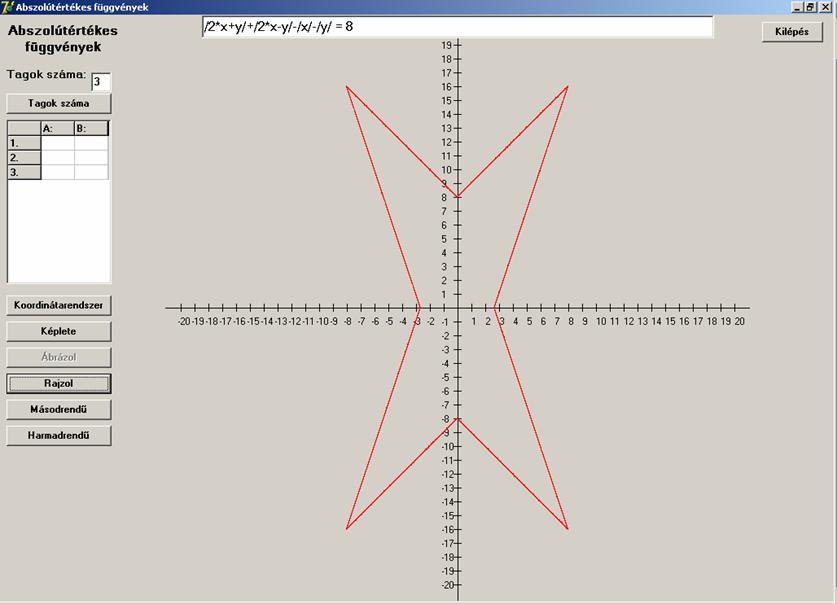
Íme egy ilyen:

Ez talán csillag, talán nem, mindenki döntse el magában.

Matematikusok számára ismerős lehet a Dirichlet-féle függvény. Aki nem ismerné, ez egy olyan függvény, amely bármely valós számra értelmezett, de sehol sem folytonos. Definíciója: a függvény értéke egy, ha független változó racionális és nulla, ha irracionális. A képe – legalább is látszólag – az x tengely és az x tengellyel párhuzamos, az y tengelyt a (0, 1)-ben metsző egyenes. Látszólagos, mert nem tudjuk csak racionális, vagy csak az irracionális pontokat megrajzolni az egyeneseken, mert mindkét számhalmaz a számegyenesen mindenütt sűrűn helyezkedik el, azaz bármely pontnak, bármilyen kis környezetében van racionális és irracionális szám is. Azt, hogy nem folytonos, épp ezen tulajdonsága alapján lehet belátni. A folytonosság definíciója szerint: a függvénynek a pontban léteznie kell határértékének és ennek meg kell egyezni a behelyettesítési értékkel. De a határérték nem létezik azért, mert bármely ponthoz található olyan a ponthoz konvergáló sorozat, amely csak racionális számokból áll, ezeken a függvényérték 1, azaz 1-hez tartanak, és létezik szintén bármely ponthoz olyan a ponthoz konvergáló csak irracionális számsorozat, amelyhez tartozó függvényértékek mind nullák, így 0-hoz tartanak. Azaz a függvénynek egyetlen pontjában még határértéke sincs (mivel a 0 nem egyenlő 1-gyel), nem hogy folytonos lenne. (Csak érdekességként: az a függvény, amely racionális számhoz önmagát, irracionálisra számhoz pedig a negatívját rendeli, egyetlen pontban, a (0, 0)-ban folytonos. Képe az y=x és az y=-x egyenesekre esik.)

Hogy jön a csizma az asztalra? Azaz mit keres itt a Dirichlet-függvény? A most említett függvény sehol sem folytonos. Az alap abszolútértékes-függvény (az y=/x/) viszont a (0, 0)-ban nem differenciálható. Láttuk, hogy az abszolútértékes-függvények számos törésponttal rendelkezhetnek. Nem kreálhatnánk-e egy olyan függvényt, amely legalább egy intervallumon, az intervallum minden pontjában folytonos, viszont az intervallum egyetlen pontjában sem deriválható. Tegyünk próbát. Nézzük a következő függvénysort.

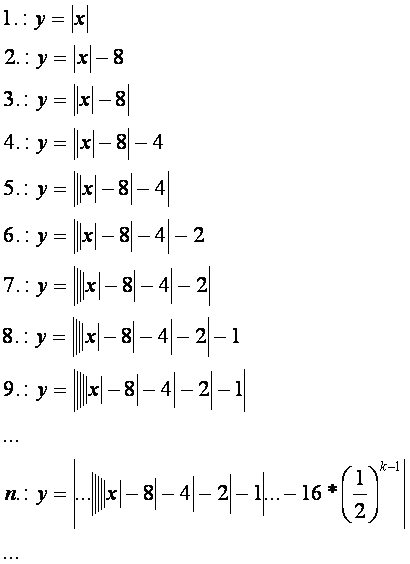, ahol n=2*k+1.

De ne csak nézzünk, ábrázoljunk is. A függvények képe nagyon árulkodó. Lássuk, mondjuk először a harmadikat:

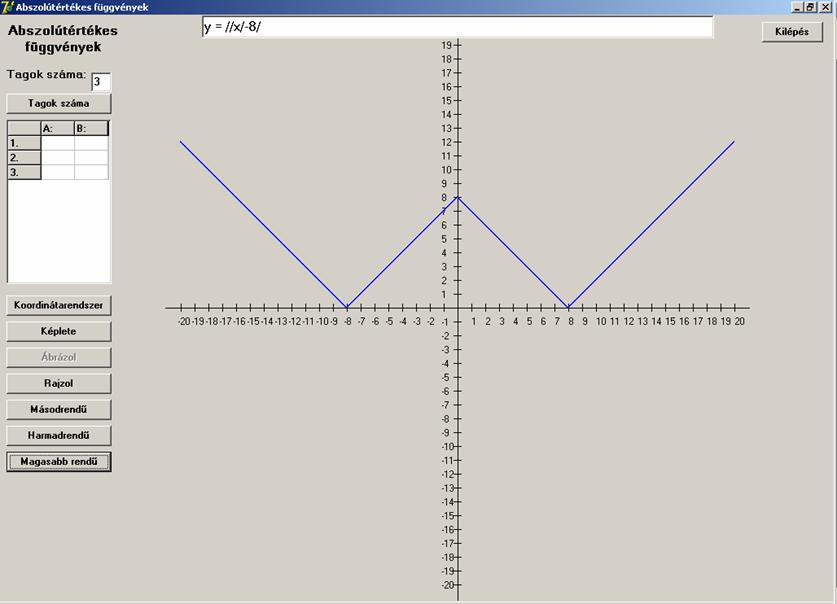
Most a hetediket:

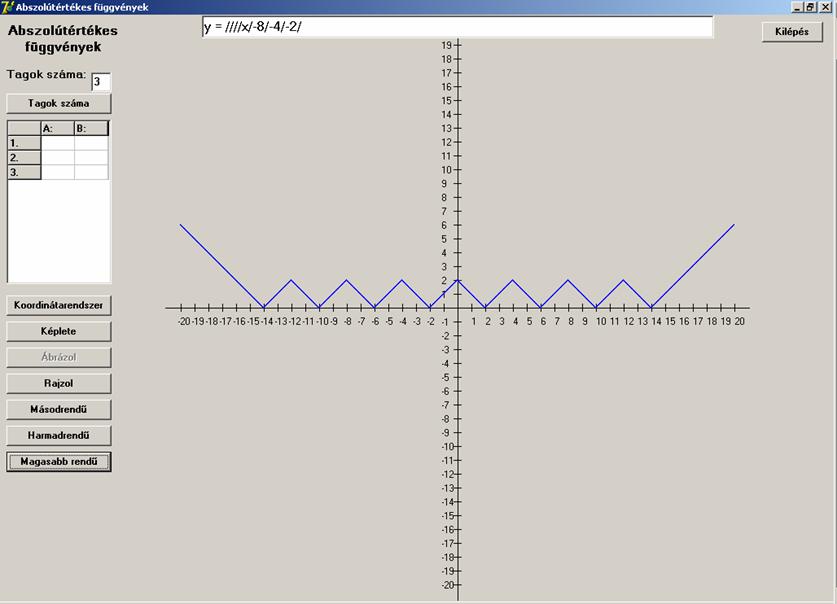
Majd a kilencediket:

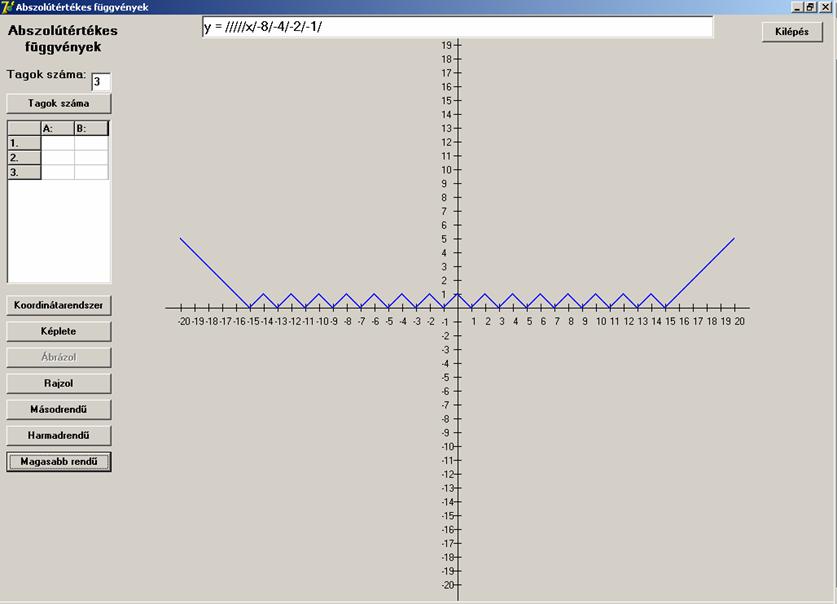
És egy még későbbit, mondjuk a 13. tagját a sornak:

Remélem világos, hogy mire megy ki a játék. Egy olyan függvényhez közelítünk, amely az értelmezési tartománya -16<=x<=16 intervallumának bármely pontja, bármely környezetében található +1 és -1 meredekségű egyenes szakasz is, azaz itt nem deriválható.

A függvénysor határfüggvényének képlete:

És így néz ki:

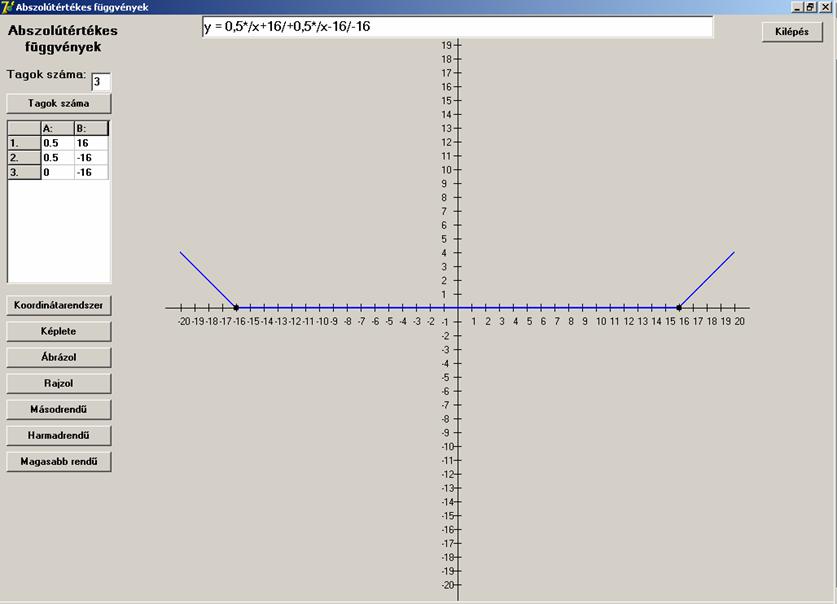
Amely a -16<=x<=16 intervallum egyetlen pontjában sem deriválható.